Grundlagen der MRT (MRI) Ͷ Grundprinzip, Messtechnik
Werbung
Grundlagen der MRT (MRI) Ͷ Grundprinzip, Messtechnik
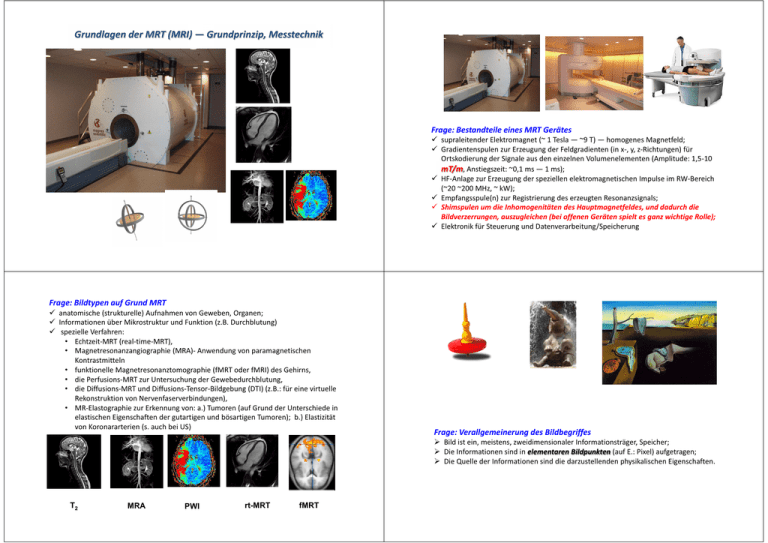
&ƌĂŐĞ͗ĞƐƚĂŶĚƚĞŝůĞĞŝŶĞƐDZd'ĞƌćƚĞƐ
9 supraleitender Elektromagnet (~ 1 Tesla Ͷ ~9 T) Ͷ homogenes Magnetfeld;
9 Gradientenspulen zur Erzeugung der Feldgradienten (in x-, y, z-ZŝĐŚƚƵŶŐĞŶͿĨƺƌ
Ortskodierung der Signale aus den einzelnen Volumenelementen (Amplitude: 1,5-10
mT/m, Anstiegszeit: ~0,1 ms Ͷ 1 ms);
9 HF-Anlage zur Erzeugung der speziellen elektromagnetischen Impulse im RW-Bereich
(~20 ~200 MHz, ~ kW);
9 Empfangsspule(n) zur Registrierung des erzeugten Resonanzsignals;
9 Shimspulen um die /ŶŚŽŵŽŐĞŶŝƚćƚĞŶ des Hauptmagnetfeldes, und dadurch die
ŝůĚǀĞƌnjĞƌƌƵŶŐĞŶ͕ĂƵƐnjƵŐůĞŝĐŚĞŶ;ďĞŝŽĨĨĞŶĞŶ'ĞƌćƚĞŶƐƉŝĞůƚĞƐŐĂŶnjǁŝĐŚƚŝŐĞZŽůůĞͿ͖
9 ůĞŬƚƌŽŶŝŬĨƺƌ^ƚĞƵĞƌƵŶŐƵŶĚĂƚĞŶǀĞƌĂƌďĞŝƚƵŶŐͬ^ƉĞŝĐŚĞƌƵŶŐ
Frage: Bildtypen auf Grund MRT
9 anatomische (strukturelle) Aufnahmen von Geweben, Organen;
9 /ŶĨŽƌŵĂƚŝŽŶĞŶƺďĞƌDŝŬƌŽƐƚƌƵŬƚƵƌƵŶĚ&ƵŶŬƚŝŽŶ;nj͘͘ƵƌĐŚďůƵƚƵŶŐͿ
9 spezielle Verfahren:
Echtzeit-MRT (real-time-MRT),
Magnetresonanzangiographie (MRA)- Anwendung von paramagnetischen
Kontrastmitteln
funktionelle Magnetresonanztomographie (fMRT oder fMRI) des Gehirns,
die Perfusions-MRT zur Untersuchung der Gewebedurchblutung,
die Diffusions-MRT und Diffusions-Tensor-Bildgebung (DTIͿ;nj͗͘͘ĨƺƌĞŝŶĞǀŝƌƚƵĞůůĞ
Rekonstruktion von Nervenfaserverbindungen),
MR-Elastographie zur Erkennung von: a.) Tumoren (auf Grund der Unterschiede in
ĞůĂƐƚŝƐĐŚĞŶŝŐĞŶƐĐŚĂĨƚĞŶĚĞƌŐƵƚĂƌƚŝŐĞŶƵŶĚďƂƐĂƌƚŝŐĞŶdƵŵŽƌĞŶͿ͖ď͘ͿůĂƐƚŝnjŝƚćƚ
von Koronararterien (s. auch bei US)
Frage: Verallgemeinerung des Bildbegriffes
¾ ŝůĚŝƐƚĞŝŶ͕ŵĞŝƐƚĞŶƐ͕njǁĞŝĚŝŵĞŶƐŝŽŶĂůĞƌ/ŶĨŽƌŵĂƚŝŽŶƐƚƌćŐĞƌ, Speicher;
¾ Die Informationen sind in elementaren Bildpunkten (auf E.: Pixel) aufgetragen;
¾ Die Quelle der Informationen sind die darzustellenden physikalischen Eigenschaften.
T2
MRA
PWI
rt-MRT
fMRT
Kontrastverfahren
&ƌĂŐĞ͗tĞůĐŚĞƉŚLJƐŝŬĂůŝƐĐŚĞŶŝŐĞŶƐĐŚĂĨƚĞŶƐŝŶĚĨƺƌMRT-Bilder benutzt?
¾
¾
¾
¾
Protonen-Dichte ďĞŝŐĞǁƂŚŶůŝĐŚĞŶ͕WƌŽƚŽŶ-MRT, Aufnahmen;
Dichte der in der Untersuchung benutzten paramagnetischen Atomkerne;
T1-Relaxationszeit;
T2-Relaxationszeit
T1
ͣtĂƐƐĞƌŬĂƌƚĞ͞eines Patienten mit Hirntumor (links) im Vergleich zu einem gesunden
Probanden (rechts). Der Wasserinhalt ist im Bereich des Tumors als auch im kompletten
'ĞŚŝƌŶŝŵsĞƌŐůĞŝĐŚnjƵŵ,ŝƌŶĞŝŶĞƐŐĞƐƵŶĚĞŶWƌŽďĂŶĚĞŶƐƚĂƌŬĞƌŚƂŚƚ͘
http://www.fz-juelich.de; Bilderzeugung auf Grund Protonendichte
T2
PD
Frage: Kontrast bei bildgebenden Verfahren
Ğƌ<ŽŶƚƌĂƐƚŝƐƚĞŝŶhŶƚĞƌƐĐŚĞŝĚƵŶŐƐŵĞƌŬŵĂůĨƺƌĚŝĞŝĨĨĞƌĞŶnjĞŶnjǁŝƐĐŚĞŶ
zwei Bildpunkten.
Frage: Unterschied zwischen gequantelten und klassischen Systemen
;/ŶĚĞƌWŚLJƐŝŬǀĞƌƐƚĞŚƚŵĂŶƵŶƚĞƌYƵĂŶƚŝƐŝĞƌƵŶŐĚĞŶmďĞƌŐĂŶŐĞŝŶĞƌŬůĂƐƐŝƐĐŚĞŶdŚĞŽƌŝĞĚĞƌWŚLJƐŝŬ
in die entsprechende quantentheoretische Darstellung. )
Fragen zu beantworten:
Welche sind die physikalischen Grundlagen der MRT?
Wie kann man die Protonendichte messen/bestimmen?
Welche sind die paramagnetischen Atomkerne?
Was sind diese Relaxationszeiten?
tŝĞŬĂŶŶŵĂŶĚĞƌƵŶƚĞƌƐĐŚŝĞĚůŝĐŚĞŶŐĞŵĞƐƐĞŶĞŶ'ƌƂƘĞŶŶĂĐŚ
kontrastieren?
ŝĞƐĞƌmďĞƌŐĂŶŐďĞŝŶŚĂůƚĞƚƵŶƚĞƌĂŶĚĞƌĞŵ͕ĚĂƐƐEnergie zwischen Systemen nur in
Quanten ausgetauscht werden kann und ĚĂƐƐƐƚĂƚŝŽŶćƌĞ^LJƐƚĞŵĞĚŝƐŬƌĞƚĞ
Energieniveaus aufweisen. Bislang sind Quantisierungen bei den folgenden
ƉŚLJƐŝŬĂůŝƐĐŚĞŶ'ƌƂƘĞŶďĞŬĂŶŶƚ͗Materie, Licht, Energie, Ladung, Impuls,
Drehimpuls, Widerstand.
Frage: ĞǁĞŝƐĞĨƺƌYƵĂŶƚĞůƵŶŐ;Ƶ͘Ă͘Ϳ:
Frage: Wie ist der Drehimpuls (L) in der klassischen Physik definiert?
Anregungs-/Absorptionsspektren von atomaren Systemen unter idealem
wechselwirkungsfreien Zustand;
Spektren von D-, J-Strahlungen (E-Strahlung steht nicht im Widerspruch!)
usw.
Der Drehimpuls eines Massenpunktes ist gleich dem Kreuzprodukt eines
Ortsvektors (r) und Impulses (ŵͼv) (senkrechte Komponenten tragen bei):
L ist gerichtet senkrecht zur Ebene von r und v!
Rechte-Hand-Regel*
m
L: ƌŚĂůƚƵŶŐƐŐƌƂƘĞ!
l=|L|=ƌͼŵ ͼǀсŵ ͼƌ ͼǀсŵ ͼƌ ͼrZ=m ͼr2 ͼZ
l=ŵͼr2 ͼZ
m: Masse des <ƂƌƉĞƌƐ/Teilchens;
Z: Kreisfrequenz;
r: Radius der Bahn
der Bahndrehimpuls
das magnetische Moment
(M oder P
P
e-(q,m)
ĨƺƌůĞŬƚƌŽŶ͗P und L sind
entgegengerichtet wegen
negativer Ladung des
Elektrons
&ƌĂŐĞ͗tĂƌƵŵďĞƐŝƚnjĞŶĚŝĞůĞŬƚƌŽŶĞŶĞŝŶĞƐƚŽŵƐͬDŽůĞŬƺůƐƌĞŚŝŵƉƵůƐ͍
s Ͷ sharp; p Ͷ principal;
9 Bahnenstruktur z.B.: H: 1s; He: 1s2; 126C: 1s22s22p2,....
d Ͷ diffuse; f Ͷ fundamental
!ABER!!!
¾ Bei s-Bahnen LсϬ;ƵŶĂďŚćŶŐŝŐǀŽŶĞƐĞƚnjƵŶŐƐnjĂŚů͖ŬƵŐĞůƐLJŵŵĞƚƌŝƐĐŚĞĂŚŶͿ
¾ Bei vollbesetzten weiteren Bahnen L=0, sonst ist LтϬ
&ƌĂŐĞ͗tĂƐĨƺƌtĞƌƚĞŬĂŶŶĚĞƌƌĞŚŝŵƉƵůƐďĞŝĂƚŽŵĂƌĞŶ^LJƐƚĞŵĞŶ
aufweisen?
An sehr kleinen physikalischen Systemen wie Atomen zeigt sich, dass der
Drehimpuls gequantelt ist. Sein Betrag kann nur ganz- oder halbzahlige
Vielfache, mL , des Planckschen Wirkungsquantums annehmen: Lz=mLͼŚ
q 2
Zr
2
e-(q,m)
M
L
P
q mZr 2
2 m
q
L
2m
&ƌĂŐĞ͗tĂƌƵŵďĞƐŝƚnjĞŶĚŝĞůĞŬƚƌŽŶĞŶĞŝŶĞƐƚŽŵƐͬDŽůĞŬƺůƐŵĂŐŶĞƚŝƐĐŚĞƐ
Moment?
9 Bahnenstruktur z.B.: H: 1s; He: 1s2; 126C: 1s22s22p2,....
!ABER!!!
¾ Bei s-Bahnen MсϬ;ƵŶĂďŚćŶŐŝŐǀŽŶĞƐĞƚnjƵŶŐƐnjĂŚů͕kugelsymmetrische Bahn)
¾ Bei vollbesetzten weiteren Bahnen MсϬ͕ƐŽŶƐƚDтϬ͊
Frage: Ist das magnetische Moment eines Elektrons auf einer Bahn
gequantelt?
9 Ja.
9 ĨƺƌĂŚŶĞŶ͗mL ist ganzzahlig!
9 ͊Z͊Ĩƺƌs-Bahnen ist es Null.
P
q
q
L
mL h
2m
2m
Frage: tĂƌƵŵďĞƐŝƚnjĞŶĚŝĞůĞŬƚƌŽŶĞŶͬEƵŬůĞŽŶĞŶĞŝŶĞƐƚŽŵƐͬDŽůĞŬƺůƐ
Drehimpuls?
9 ĂŚŶĞŶƐƚƌƵŬƚƵƌĨƺƌůĞŬƚƌŽŶĞŶ;Ɛ͘ŽďĞŶͿ
9 + Eigendrehimpuls
= SPIN
Der Spin ist gequantelt. Der Betrag seiner Projektion auf eine vorgegebene
Richtung kann nur ganz- oder halbzahlige Vielfache des Planckschen
Wirkungsquantums annehmen; seine Einheit ist :ͼƐ!!
&ƌĂŐĞ͗tĂƐĨƺƌĞŝŶĞŶ^ƉŝŶďĞƐŝƚnjĞŶĚŝĞͣĞůĞŵĞŶƚĂƌĞŶ͞dĞŝůĐŚĞŶ͍
Elektron, Positron, Proton, Neutron,... 1/2 {Js}
Photonen: 1
Frage: sĞƌŬŶƺƉĨƚƐŝĐŚĚĞƌ^ƉŝŶŵŝƚŵĂŐŶĞƚŝƐĐŚĞŵDŽŵĞŶƚ͍
9
9
9
9
Ja.
njƵƐćƚnjůŝĐŚ͗ŐĞƋƵĂŶƚĞůƚ͊
mS: Spin-Quantenzahl
mS: +1/2; -1/2
P
q
S
2m
q
mS h
2m
Frage: Wie setzt sich der Spin in Atomkernen
zusammen?
E
P
9 ŐĞƚƌĞŶŶƚĞ^ĐŚĂůĞŶƐƚƌƵŬƚƵƌĨƺƌWƌŽƚŽŶĞŶƵŶĚ
Neutronen.
9 njƵƐćƚnjůŝĐŚ͗ŐĞƋƵĂŶƚĞůƚ͊
9 mS: mS,P+mS,N
z.B.: mS,P+mS,N=1/2+1/2=1
Frage: Was bedeutet die Energieentartung?
&ƌĂŐĞ͗tĂƐŝƐƚĚĂƐ'ƌƵŶĚƉŚćŶŽŵĞŶĨƺƌDZd͍
ĨƺƌůĞŬƚƌŽŶĞŶĞŝŶĞƐƚŽŵƐ͗
9 ŽŚŶĞćƵƘĞƌĞtĞĐŚƐĞůǁŝƌŬƵŶŐͬŝŶǁŝƌŬƵŶŐŝƐƚĚŝĞŶĞƌŐŝĞ
durch die Haupt-, und Nebenquantenzahlen bestimmt;
9 ĚĞƌŶĞƌŐŝĞnjƵƐƚĂŶĚŝƐƚŝŶĚŝĞƐĞŵ&ĂůůƵŶĂďŚćŶŐŝŐǀŽŶ
weiteren Quantenzahlen!
ĨƺƌƚŽŵŬĞƌŶĞ͗
9 ƵŶĂďŚćŶŐŝŐǀŽŶ^ƉŝŶnjƵƐƚćŶĚĞŶ der Protonen und
Neutronen besitzt der Atomkern dieselbe Energie
Frage: Wie kann die Energieentartung aufgehoben werden?
Wenn sich die emittierende Materie in einem externen Magnetfeld befindet,
ŬƂŶŶĞŶĚŝĞ^ƉĞŬƚƌĂůůŝŶŝĞŶĂƵĨƐƉĂůƚĞŶ;ĞŽďĂĐŚƚƵŶŐǀŽŶW͘ĞĞŵĂŶ;ϭϴϵϲͿͿͶ
Zeemansche Aufspaltung.
ŝĞŶnjĂŚůĚĞƌƵŶƚĞƌƐĐŚŝĞĚůŝĐŚĞŶŶĞƌŐŝĞŶŝǀĞĂƵƐŚćŶŐƚǀŽŶĚĞƌ'ƌƂƘĞĚĞƌ
Magnetische- und Spinquantenzahl ab.
Im Allgemeinem, ist die Spinzahl gleich mS, ist die Anzahl der Energieniveaus
gleich (2mS+1). z.B: mS=1/2, Anzahl der Niveaus = 2; mSсϭїŶсϯ
In Richtung des Magnetfeldes ist der Spin (und auch der Bahndrehimpuls)
gequantelt!
N
Der Wasserstoffatomkern besteht aus einem Proton
mS,PсϭͬϮї;2mS+1ͿсϮїnE=2; E-1/2 und E+1/2;
im Magnetfeld tritt die Aufspaltung der entarteten Energieniveaus auf:
Grundniveau und Anregungsniveau
ĚŝĞ'ƌƂƘĞĚĞƌƵĨƐƉĂůƚƵŶŐŚćŶŐƚǀŽŶĚĞƌ&ĞůĚƐƚćƌŬĞĂď
njǁŝƐĐŚĞŶĚĞŶŶĞƌŐŝĞŶŝǀĞĂƵƐŬĂŶŶŵĂŶmďĞƌŐćŶŐĞĚƵƌĐŚĞƐƚƌĂŚůƵŶŐŵŝƚ
geeigneter elektromagnetischer Strahlung induzieren
E+1/2
E-1/2
&ƌĂŐĞ͗tŝĞŐƌŽƘŝƐƚĚŝĞŶĞƌŐŝĞĚŝĨĨĞƌĞŶnjnjǁŝƐĐŚĞŶnjǁĞŝEŝǀĞĂƵƐĨƺƌ
eine Spinquantenzahl von mS?
9 'H=konst*'mS*H
9 'mS darf nur Eins sein!
9 Aufgrund des Drehimpulserhaltungssatzes: 'l=0; das absorbierte Photon
ďĞƐŝƚnjƚĞŝŶĞŶƌĞŚŝŵƉƵůƐϭї
Zu Rechenaufgaben:
οߝ ൌ ்݃ ή ߤ ் ή ܪ
்݃ : Lande-Faktor eines Teilchens;
ߤ ் : Magneton des Teilchens;
s. Dia 15.
|ge|=2.002319; gP=5.5856912; |gN|=3.82608545
ߤே ൌ ͷǤͲͷͲͺͶͳͲିଶ ܬȀܶ
ߤ ൌ ͻǤʹͳͲିଶସ ܬȀܶ
ߤ௧௦௦ ൌ ߤெ௧
Kernmagneton
Bohr-Magneton: das Magneton des Elektrons
E+1/2
οߝ ൌ ݃ ή ߤே ή ܪ
'HP= ϱ͘ϱϴϱϲϵϭϮΎϱ͘ϬϱϬϴϰͼϭϬоϮϳ ܬ/ܶ*H(T)
'HP= 2.82124325ͼϭϬо26 ܬ/ܶ * H(T)
'H=konst*H
'HP(H=1T) = Ϯ͘ϴϮϭϮϰϯϮϱͼϭϬоϮϲ ܬ
E-1/2
'HP(H=1T) =
Ϯ͘ϴϮϭϮϰϯϮϱͼϭϬоϮϲܬ
Ǥήషૢ ࡶȀࢋࢂ
'HP(H=1T) =1.76327703ͼϭϬоϳ eV
=
H.Aufg.: Vergleich mit durchschnittlicher kinetischen Energie = (kT)
Wie groƘist die Frequenz?
ŚĂƌĂŬƚĞƌŝƐƚŝƐĐŚĞ'ƌƂƘĞŶ͗
Frequenzbereich
'HP=h*f= 2.82124325ͼϭϬо26 ܬ/ܶ * H(T)
f=
Ϯ͘ϴϮϭϮϰϯϮϱͼϭϬоϮϲܶͬܬ
* H(T)=42.5771175 MHz/T
ϲ͘ϲͼϭϬоϯϰܬήƐ
f=42.5771175 MHz/T* H(T)
Rechenaufgabe:
Bei einer Protonen-MRT-Untersuchung ist die benutzte magnetische FeldstćƌŬĞ 3,5 T.
a.) Wie ŐƌŽƘ muss die Radiowellenfrequenz sein?
b.) Wie ŐƌŽƘ ist die Energiedifferenz, in eV-Einheiten, zwischen den Grund- und
angeregten ƵƐƚćŶĚĞŶ der Zeemanschen Niveaus?
c.) Das Wievielfache der thermischen kinetischen Energie entspricht der oben
berechneten Anregungsenergie?
)HOGVWlUNHWHVOD
'H (J)
'H (eV)
40-200 MHz
~0,9 ² ~10
Â-26 ² Â-25
Â-7 ² Â-6
Besetzungsdifferenz bezogen
auf Besetzung des Grundniveau
ā-6 ²ā-5
gesamte absorbierte Energie (J)
im Falle einer
Populationsinversion
ā-15 ² ā-12
Frage: Wie kann man die Protonendichte bestimmen?
ܮ
DŝƚƚĞůƵŶŐƺďĞƌĂůůĞ^ƉŝŶƐnjƵĞŝŶĞŵĞŝƚƉƵŶŬƚ.
&ƌĂŐĞ͗tĂƐĨƺƌƚŽŵŬĞƌŶĞƐŝŶĚĨƺƌDZdŶŽĐŚŐĞĞŝŐŶĞƚ?
E
Atomkerne die von Null unterschiedlichen Spin besitzen
Ungepaarte Protonen und/oder Neutronen
z.B.: 2H, 13C, 15N, 17O, 19F, 23Na, 31P
E
E2
E(H=0)
' H
E1
H=0
molekulare Veranschaulichung des magnetischen Moments
z
z
magnetisches Moment ( M)
H
M=Mz=Meq
M=M z=0
P
P
P
y
M=6P i
P
P P P P
y
M=6
6P i
P P P P P
P
P
P
P
P
P
P P
P
P
P P P P P
P
P P P P
P
P
PP
x
x
H =0; M =0
&ƌĂŐĞ͗tŝĞŐƌŽƘŝƐƚĚŝĞŝĨĨĞƌĞŶnjŝŶĞƐĞƚnjƵŶŐ͍
9 Sie ist durch die Boltzmannsche Verteilung beschrieben.
H> 0; M> 0
Frage: Was ist die Konsequenz einer RF-Anregung
^ŝĞŚćŶŐƚǀŽŶĚĞƌĚƵƌĐŚĞŝŶĞŶZ&-/ŵƉƵůƐnjƵŐĞĨƺŚƌƚĞŶŶĞƌŐŝĞŵĞŶŐĞĂď
90o und 180o Impulse
Registrierung der Signale mit Empfangsspulen nach dem Impuls zu gewisser
Zeitspanne.
Signale werden beobachtet entlang x, y (und z) ZŝĐŚƚƵŶŐĞŶǁćŚƌĞŶĚĚĞƌ
Entspannung (Relaxation ) der angeregten Atomkerne
n2
n1
e 'H / kT
Rechenaufgabe:
Bei einer Protonen-MRT-Untersuchung ist die benutzte magnetische FeldstćƌŬĞ 1,5 T.
a.) Wie ŐƌŽƘ ist das ĞƐĞƚnjƵŶŐƐǀĞƌŚćůƚŶŝƐ der Grund- und angeregten Niveaus?
b.) Wie viele Protonen ǁćƌĞŶ im Angeregten Zustand, wenn die Anzahl der Protonen
im Grundzustand no=107 ist.
c.) Wie ŐƌŽƘ ist die Anzahl der Protonen im angeregten Zustand nach einer 90o-Puls?
Grundgrößen
Besetzung der Niveaus:
gP= 5.5856912
z
Anregung
z
E
E2
n1
n2
PN[J/T]= 5.05E-27
Gleichung zw. Energie und
Feldstärke
M=M xy
Beispiel:
H[T]= 1
y
E1
' H [J] = 2.8212E-26
Beispiel:
x
gleichzeitige Drehung
H[T]= 1
d(Schicht)[mm]= 2
r[cm]= 25
t[oC]= 37
kT= 4.27924E-21
'e[J]= 2.82E-26
A=(r^2*S)[cm2]= 1963.495408
e -'H/kT= 0.999993407
V(Schicht)[cm3]= 392.6990817
U Gew. [g/cm3] 1.04
m(Schicht)[g]= 408.407045
nP=NA*mSchicht/MH= 2.45861E+26
'n= 8.10465E+20
'n/2= 4.05232E+20
EBestrahlung[J]= 1.14E-05
PBestrahlung[kW]= 0.5
no=nP= 2.45861E+26 'tBestrahlung[Ps]=E/P= 0.0229
&ƌĂŐĞ͗tŽǀŽŶŚćŶŐƚĚŝĞZĞůĂdžĂƚŝŽŶ;szeit) ab?
&ƌĂŐĞ͗tĂƐŝƐƚĚĞƌ'ƌƵŶĚĨƺƌ^ŝŐŶĂůƵŶƚĞƌƐĐŚŝĞĚĞnjǁŝƐĐŚĞŶƵŶƚĞƌƐĐŚŝĞĚůŝĐŚĞŶ
Geweben
von Atomsorte
von Verbindungen in denen sich die untersuchten Atomkerne
befinden
9 ĐŚĞŵŝƐĐŚĞƵĨďĂƵ͕^ƚƌƵŬƚƵƌĚĞƌDŽůĞŬƺůĞ
9 Wechselwirkung mit eigenen und mit Elektronen der
ďĞŶĂĐŚďĂƌƚĞŶƚŽŵĞŶͬDŽůĞŬƺůĞŶ
W
ͻ ŝĞ&ĞůĚƐƚćƌŬĞĚĞƐĞdžƚĞƌŶĞŶŵĂŐŶĞƚŝƐĐŚĞŶ&ĞůĚĞƐǁŝƌĚĚƵƌĐŚĚŝĞůŽŬĂůĞŶ
tĞĐŚƐĞůǁŝƌŬƵŶŐĞŶǀĞƌćŶĚĞƌƚͶ lokales magnetisches Feld.
ͻ ŝĞŶƌĞŐƵŶŐƐĨƌĞƋƵĞŶnj͕ĚŝĞ^ŝŐŶĂůĂŵƉůŝƚƵĚĞŚćŶŐƚǀŽŶĚĞƌhŵŐĞďƵŶŐĚĞƐ
Protonenspins Ͷ von molekularen Zusammensetzung/Aufbau eines Gewebes
&ƌĂŐĞ͗tŝĞćŶĚĞƌƚƐŝĐŚĚĂƐ^ŝŐŶĂůŵŝƚĚĞƌZĞůĂdžĂƚŝŽŶƐnjĞŝƚ͍
ŬƺƌnjĞƌĞZĞůĂdžĂƚŝŽŶƐnjĞŝƚĨƺŚƌƚnjƵŬůĞŝŶĞƌĞŶ^ŝŐŶĂůĂŵƉůŝƚƵĚĞŶ
DƂŐůŝĐŚŬĞŝƚĨƺƌƉĂƌĂŵĂŐŶĞƚŝƐĐŚĞƵƐůƂƐĐŚƵŶŐͬsĞƌŵŝŶĚĞƌƵŶŐĚĞƌ
Signalamplitude
9 Kontrastverfahren mit Gd-ŚĂůƚŝŐĞŶDŽůĞŬƺůĞŶ
9 mit paramagnetischen (z.B. nitroxid-Typ) freien Radikalen
¾ Perfusion/Durchblutungsversuchen
¾ Angiographie
H
P
P
H
H
P H
H
P
P
H
choline-haltige Verbindungen (Cho)
z.B.: glycerophosphocholin, cholin, phosphatidylcholin͕͙
&ƌĂŐĞ͗tŝĞŬƂŶŶĞŶĚŝĞZĞůĂdžĂƚŝŽŶƐnjĞŝƚĞŶďĞƐƚŝŵŵƚǁĞƌĚĞŶ͍
z
E
H ist schon angelegt:
Aufspaltung der
Energieniveaus
E
E
E2
E2
t
Relaxation
E1
E2
E1
M=Mz
y
E1
z
x
z
M
M
y
y
90o-Impuls
x
Aufbau/Abbau von
Mz/Mxy sind XQDEKlQJLJ
² doch gleichzeitig
Mxy
t
E
E2
=HLWOLFKH$EKlQJLJNHLWGHUx-y Komponente
des Relaxationsprozesses; Spin-Spin
Relaxation; T2-Relaxationszeit
z
n1
n2
M=Mxy
y
E1
x
x
Mz
t
=HLWOLFKH$EKlQJLJNHLWGHU] Komponente
des Relaxationsprozesses; Spin-Gitter
Relaxation; T1-Relaxationszeit
Frage: Wie ŬƂŶŶĞŶ die Relaxationszeiten bestimmt werden?
9 Hauptmagnetfeld ist angelegt
9Anregung mit elektromagnetischem Impuls (90o oder 180o)
9Registrierung der Echo-Signale zu gewisser Zeit nach Anregung
9Wiederholung der Anregung/Registrierungsprozesse Ͷ MRT-Sequenzen
S ~ U eTE / T2 (1 eTR / T1 )
Frage: Sind immer die selben Puls(Anregungs)sequenzen und
Empfangssequenzen benutzt?
9 Nein Ͷ ŚćŶŐƚǀŽŶĚĞŶnjƵƵŶƚĞƌƐƵĐŚĞŶĚĞŶ'ĞǁĞďĞŶͬMessverfahren ab
9 Anregung mit elektromagnetischem Impuls (90o oder 180o) Ͷ
Repetitionszeit (TR)
9 Auslesen der Echo-Signale zu gewisser Zeit nach Anregung Ͷ Echozeit (TE)
S ~ U eTE / T2 (1 eTR / T1 )
TR: Repetitionszeit: Wiederholung einer bestimmten Sequenz von RF-Anregungen
und magnetischen Feldgradienten; Wie viele Spins sind umgeklappt?
TE: Echozeit, Auslesezeit der Signale; Wie viele Spins sind beim Echo noch in Phase?
ܶா ܶ بଶ ՜ ݁ ି்ಶ Τ்మ ՜ ݁ ିé
Protonendichte
ܶா ܶ اଶ ՜ ݁ ି்ಶ Τ்మ ՜ ݁ ି ൎ ͳ
kein Signal mehr
Auslese kurz nach Anregung;
maximale Signalamplitude
Kontrastverfahren aufgrund U, T2, T1 mit geeigneter Wahl Ĩƺƌ TE und TR;
TE und TR sind durch T2 und T1 beeinflusst.
Frage: Wie sieht eine MRI-Sequenz aus?
Protonendichte-Wichtung: TR lang; TE kurz
S ~ U eTE / T2 (1 eTR / T1 )
Hilfsgradienten
Protonendichte-Wichtung: TR lang; TE kurz
9 ŝŶĞůĂŶŐĞZĞƉĞƚŝƚŝŽŶƐnjĞŝƚĨƺŚƌƚnjƵŬĞŝŶĞŵŶĞŶŶĞŶƐǁĞƌƚĞŶEinfluss der T1-Zeit auf
das Bild. (Das zweite Glied ist ~1).
9 Eine kurze Echozeit bedeutet, dass auch kein beobachtbarer Einfluss der T2-Zeit
existiert. (Das erste Glied ist ~1).
9 Der einzige Unterschied besteht nunmehr in der 'ƌƂƘe der
Gleichgewichtsmagnetisierung. Gewebe mit unterschiedlicher
Protonenzahldichte sind somit bei dieser Parametereinstellung unterscheidbar.
T1-Relaxation
T1-Kontrast Ͷ maximal bei TR~=T1
TE<<T2 um T2 ďŚćŶŐŝŐŬĞŝƚnjƵŵŝŶŝŵŝĞƌĞŶ͖
TR kurz; TE kurz
topt.: ~ 600 ms
T1 [ms]
Fett: 240
weise Substanz:680
graue Substanz:809
Liquor: 2500
Fett hell
Liquor dunkel
Frage: Was ist die Rolle der magnetischen Feldgradienten
T2-Kontrast Ͷ maximal bei TE~=T2
TR>>T1 um T1 ďŚćŶŐŝŐŬĞŝƚnjƵŵŝŶŝŵŝĞƌĞŶ
TR lang; TE lang
H
hQ
1
z
0.9
T2 [ms]
Fett: 84
w. Subst.: 92
g. Subst.: 101
Liqu.: 1400
M xy/Mo
0.8
0.7
1
0 .9
0.6
Mz,Fett
Mz,w.S.
0 .8
Mz.g.S.
0 .7
0.5
Mz,Liq.
0 .6
0 .4
0 .3
0.3
hQ
H
Resonanz nur in dieser Schicht
0 .5
0.4
E
Die Amplitude des NMR-Signals ist proportional zur
Protonenkonzentration der gegebenen Schicht.
0 .2
0 .1
0.2
0
0
50
1 00
1 50
2 00
2 50
3 00
3 50
4 00
4 50
5 00
0.1
t [ms]
0
0
50
100
150
200
250
300
350
400
450
500
Anwendung eines entsprechenden magnetischen Feldgradienten entlang der x,y,z
Achsen Ͷ ƵŶĚƐĞŝŶĞƐĐŚƌŝƚƚǁĞŝƐĞsĞƌćŶĚĞƌƵŶŐͶ erlaubt die Bestimmung der
WƌŽƚŽŶĞŶĚŝĐŚƚĞŝŶũĞĚĞŵĞŝŶnjĞůŶĞŶsŽůƵŵĞŶĞůĞŵĞŶƚĞŝŶĞƐ<ƂƌƉĞƌƐххein Bild
gewichtet durch Protonendichte kann hergestellt werden.
Rechenaufgabe:
Bei einem Protonen-MRT Gerćƚ sei der Gz-Feldgradient 5 mT/m und die
Anregungsfrequenz 100 MHz.
a.) ĞƌĞĐŚŶĞŶ^ŝĞĚŝĞŵĂŐŶĞƚŝƐĐŚĞŶ&ĞůĚƐƚćƌŬĞŶĂŶĚĞŶZćŶĚĞƌŶĞŝŶĞƌϮ-mmDicken Gewebeschicht.
b.) Wie ŐƌŽƘ ist die Verschiebung in den Resonanzfrequenzen bei den ZćŶĚĞƌŶ?
c.) Geben Sie die relativen Frequenzverschiebungen (Gf/fo) an!
x
Gz
hQ
H
z
y
Ein Feldgradient entlang der z-Achse erlaubt die Auswahl einer Schicht
ŝĞĞƐƚƌĂŚůƵŶŐƐĨƌĞƋƵĞŶnjƵŶĚĚŝĞŵĂŐŶĞƚŝƐĐŚĞ&ĞůĚƐƚćƌŬĞďĞƐƚŝŵŵĞŶ
die Schicht wo die Protonen angeregt werden Ͷ Quelle der
registrierten Signale
Gx=GI
ŝŽƉŚLJƐŝŬĨƺƌDĞĚŝnjŝŶĞƌ
Boltzmann-Verteilung I/3.1.1
Drehmomente, Spins, magnetisches Moment, weitere Quantenerscheinungen
I/1.4.1, I/1.4.2
MRT-Methoden VIII/4.1
Relaxationsmechanismen am Ende von X/4.1
Weitere empfohlene Literatur:
http://ebookbrowse.com/luetticke-seminar-ss09-pdf-d295966112;
http://de.wikipedia.org/wiki/Magnetresonanztomografie;
http://de.wikipedia.org/wiki/Magnetresonanzangiographie;
http://de.wikipedia.org/wiki/Diffusions-TensorBildgebung/Diffusionsgewichtete_MRT-Sequenzen;
zu untersuchende Schicht
Gy=GZ
Vergleich mit Dia 32. !!!!
Ein weiterer (z.B.: Gx) Feldgradient ergibt eine
Phasenkodierung;
der andere Gradient (z.B. GyͿŝƐƚďĞŶƵƚnjƚǁćŚƌĞŶĚĚĞƌ
Auslese des Echo-Signals;
Die Koordinaten eines Punktes sind dadurch bestimmt
I
http://www.imaios.com/en/
Z
ŝŽƉŚLJƐŝŬĨƺƌDĞĚŝnjŝŶĞƌ
Boltzmann-Verteilung I/3.1.1
Drehmomente, Spins, magnetisches Moment, weitere Quantenerscheinungen
I/1.4.1, I/1.4.2
MRT-Methoden VIII/4.1
Relaxationsmechanismen am Ende von X/4.1
Weitere empfohlene Literatur:
http://ebookbrowse.com/luetticke-seminar-ss09-pdf-d295966112;
http://de.wikipedia.org/wiki/Magnetresonanztomografie;
http://de.wikipedia.org/wiki/Magnetresonanzangiographie;
http://de.wikipedia.org/wiki/Diffusions-TensorBildgebung/Diffusionsgewichtete_MRT-Sequenzen;
http://www.imaios.com/en/