Rekapitulation: Darstellung von Graphen

Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 319, Seite 77 im Skript)
Rekapitulation: Darstellung von Graphen
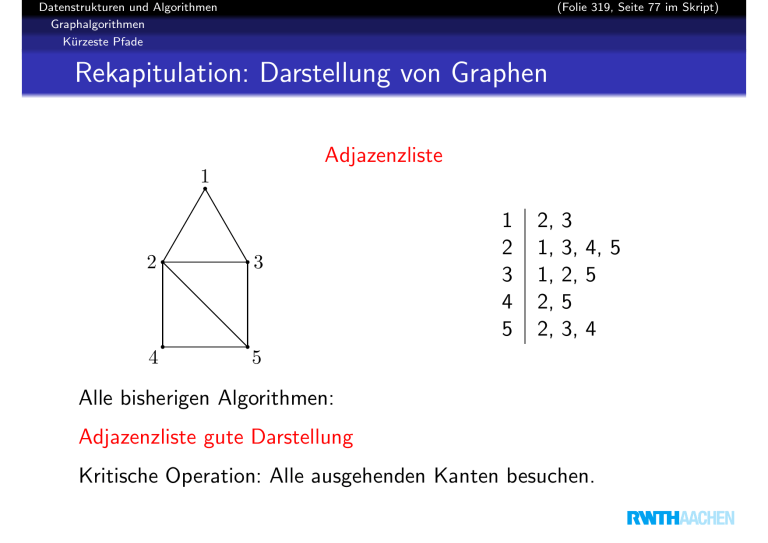
Adjazenzliste
1
2
3
4
5
1
2
3
4
5
2,
1,
1,
2,
2,
3
3, 4, 5
2, 5
5
3, 4
Alle bisherigen Algorithmen:
Adjazenzliste gute Darstellung
Kritische Operation: Alle ausgehenden Kanten besuchen.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 320, Seite 77 im Skript)
All Pairs Shortest Paths
Eingabe: Gerichteter Graph mit Kantengewichten
Ausgabe: Abstände und kürzeste Wege zwischen allen
Knotenpaaren
Laufzeit O((|V |2 + |V | · |E |) log |V |) mit Dijkstra.
→ Wende Dijkstra auf jeden Knoten an.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 321, Seite 77 im Skript)
Algorithmus von Floyd
Algorithmus
procedure Floyd1 :
for i = 1, ..., n do
for j = 1, ..., n do d[i, j, 0] := length[i, j] od
od;
for k = 1, ..., n do
for i = 1, ..., n do
for j = 1, ..., n do
d[i, j, k] := min{d[i, j, k − 1], d[i, k, k − 1] + d[k, j, k − 1]}
od
od
od
Der Abstand von i nach j ist in d[i, j, n] zu finden.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 322, Seite 77 im Skript)
Theorem
Die kürzesten Wege zwischen allen Knotenpaaren eines gerichteten
Graphen G = (V , E ) können in O(|V |3 ) Schritten gefunden
werden.
Beweis.
Per Induktion: d[i, j, k] enthält die Länge des kürzesten Pfades von
i nach j, wenn nur 1, . . . , k als Zwischenstationen erlaubt sind.
Dann enthält d[i, j, n] den wirklichen Abstand.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
Algorithmus von Floyd
Einfachere Version:
Algorithmus
procedure Floyd :
for i = 1, ..., n do
for j = 1, ..., n do d[i, j] := length[i, j] od
od;
for k = 1, ..., n do
for i = 1, ..., n do
for j = 1, ..., n do
d[i, j] := min{d[i, j], d[i, k] + d[k, j]}
od
od
od
(Folie 323, Seite 77 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 324, Seite 77 im Skript)
Spezialfall: Transitive Hülle – Algorithmus von Warshall
Frage: Zwischen welchen Knotenpaaren gibt es einen Weg?
Algorithmus
procedure Warshall :
for i = 1, ..., n do
for j = 1, ..., n do D[i, j] := A[i, j] od
od;
for k = 1, ..., n do
for i = 1, ..., n do
for j = 1, ..., n do
D[i, j] := D[i, j] || D[i, k] && D[k, j]
od
od
od
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 325, Seite 77 im Skript)
Transitive Hülle
Theorem
Wir können die transitive Hülle eines gerichteten Graphen
G = (V , E ), der k starke Zusammenhangskomponenten hat, in
O(|V | + |E 0 | + k 3 ) Schritten berechnen, wobei E 0 die Kanten der
transitiven Hülle sind.
Beweis.
1 Berechne die starken Zusammenhangskomponenten
2
Schrumpfe jede SCC X zu einem Knoten
3
Berechne die transitive Hülle H dieses Graphen
4
Für jede Kante (X , Y ) in H gib alle Kanten (x, y ) mit
x ∈ X , y ∈ Y aus.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 326, Seite 78 im Skript)
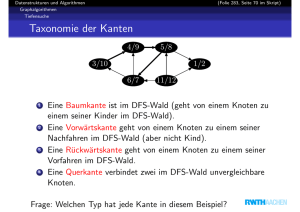
Breitensuche
7/
4/
8/
2/6
3/
1/5
Breitensuche ist das Gegenteil“ von Tiefensuche.
”
Tiefensuche: Aktive Knoten auf Stack
Breitensuche: Aktive Knoten in FIFO-Queue
Intelligente Suche: Weder Stack noch Queue
Breitensuchbaum enthält kürzeste Pfade (ungewichtet)
Discovery- und Finishzeiten wenig Anwendungen
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 327, Seite 78 im Skript)
Breitensuche
2
1
2
1
1
0
Knoten wird aktiv:
Abstand berechnen und Kante in BFS-Baum
Anwendung:
Alle Abstände und kürzesten Wege von s berechnen
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 328, Seite 78 im Skript)
Breitensuche – Größeres Beispiel
0
1
1
1
2
2
2
4
4
3
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
Java
(Folie 329, Seite 78 im Skript)
public void BFS(Node s, MaphNode, Nodei p) {
SimpleIterator hNodei it;
MaphNode, Integer i color = new HashtablehNode, Integer i();
QueuehNodei q = new QueuehNodei();
for(it = nodeiterator (); it.more(); it.step()) {
it.key ().weight = 1.0e10 ; color .insert(it.key (), 0); } // white
s.weight = 0.0; q.enqueue(s); color .insert(s, 1); // gray
while(!q.isempty ()) {
Node v = q.dequeue();
Iterator hNode, Edgei adj;
for(adj = neighbors.find(v ).iterator (); adj.more(); adj.step()) {
Node u = adj.key ();
if(color .find(u) ≡ 0) {
color .insert(u, 1); // gray
u.weight = v .weight + 1; p.insert(u, v ); q.enqueue(u);
}
}
color .insert(v , 2); // black
}
}
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 330, Seite 78 im Skript)
Breitensuche
Theorem
Gegeben sei ein gerichteter oder ungerichteter Graph G = (V , E )
und ein Knoten s ∈ V .
Die kürzesten Wege von s zu allen anderen Knoten und die
zugehörigen Abstände können in O(|V | + |E |) berechnet werden.
Beweis.
Wir verwenden Breitensuche.
Die Laufzeit ist offensichtlich linear.
Der Korrektheitsbeweis sei hier weggelassen (etwas lang und
technisch).
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
Beispiel
(Folie 331, Seite 78 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 332, Seite 78 im Skript)
Beispiel: DFS
51
50
45
44
41
40 139 141 142 143 151 150 152 153 154
52
49
46
43
42
39
53
48
47 137 138 122 37
54
55
60
61 123 121 120 131 117 33 149
136 56
59
62 124 125 119 118 116 32
135 57
58
63 127 126 132 110 111 112 30
134 69
68
64 128 129 130 109 114 113 29
133 70
67
65
98
99 100 108 104 115 28
38 140
36
144 145 146
35
34 148 147
31
72
71
77
66
97
96 101 102 103 107 27
73
75
76
78
79
95
94
93 105 106 26
25
81
80
82
83
87
88
19
20
23
24
5
6
84
85
86
89
18
21
22
7
8
92
91
90
17
16
9
10
11
12
13
14
74
4
2
1
3
15
158 159 161 163 164
155 156 157 160 162
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 333, Seite 78 im Skript)
Beispiel: BFS
77
73
59
57
53
50
47
52
56
58
71
68
72
76
80
91
88
90
94
96 100
81
69
61
55
51
48
46
49
62
60
63
65
75
78
82
84
86
93
97
99
83
66
64
45
44
43
42
70
67
79
85
87
41
74
40
39
89
98
92
95
54
37
36
38
35
34
5
7
4
6
8
2
3
18
9
10
1
17
15
13
11
12
14
16
33
32
31
26
27
30
25
28
29
23
21
24
19
20
22
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 334, Seite 78 im Skript)
Beispiel: LC
42
44
41
43
40
39
45
46
47
38
50
48
49
37
36
35
33
32
31
34
30
29
5
4
2
1
3
6
7
8
9
10
11
12
13
28
27
26
21
22
25
20
23
24
19
16
17
14
15
18
51
52
53
54
57
55
56
58
59
60
61