31.05.2011

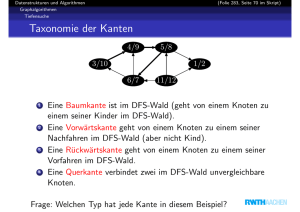
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 304, Seite 77 im Skript)
s-t Connectivity
Gegeben: Knoten s und t in gerichtetem Graph
Frage: Ist t von s erreichbar (durch einen gerichteten Pfad)?
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 305, Seite 77 im Skript)
s-t Connectivity
Führe eine DFS aus, starte bei s.
Pfad von s nach t ⇐⇒ f (t) < f (s).
19/20
7/14
8/13
17/22
3/4
9/12
18/21
15/16
10/11
1/6
2/5
Beweis: Wenn s schwarz wird, sind alle von s erreichbaren Knoten
schwarz.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 306, Seite 77 im Skript)
s-t Connectivity
Theorem
Gegeben sei ein gerichteter Graph G = (V , E ) und s ∈ V .
Wir können in linearer Zeit alle von s erreichbaren Knoten finden.
19/20
10/11
15/16
1/18
9/12
5/6
2/17
8/13
4/7
3/14
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 307, Seite 77 im Skript)
Single Source Shortest Paths
Gegeben ein gerichteter Graph G = (V , E ) mit nicht-negativen
Kantengewichten length : E → Q und ein Knoten s ∈ V , finde die
kürzesten Wege von s zu allen Knoten.
Wir lösen das Problem mit dynamischer Programmierung.
Menge F von Knoten, deren Abstand bekannt ist.
Anfangs ist F = {s}.
F wird in jeder Iteration größer.
Invariante: Kein Knoten v ∈
/ F hat kleineren Abstand zu s als
jeder Knoten in F .
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
1
1
1
(Folie 308, Seite 77 im Skript)
2
2
1
1
s 0
3
9
5
9
3
2
3
Grüne Knoten: F
1
∞
Roter Knoten aktiv,
relaxiert seine
Nachbarn
Weiße Knoten
enthalten Abstand zu
s über grüne Knoten.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 309, Seite 77 im Skript)
Korrektheit
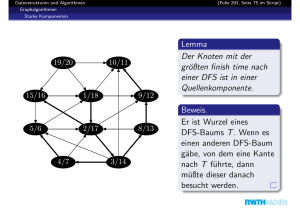
Lemma
Jeder grüne Knoten enthält den Abstand von s.
Jeder weiße Knoten enthält Abstand von s über grüne Knoten.
Beweis.
Sei v einer weißer Knoten, dessen Beschriftung minimal ist.
Betrachte einen kürzesten Pfad von s nach v und den ersten
weißen Knoten u auf diesem Pfad.
Es gilt u = v , da der Abstand von s zu u mindestens so groß ist
wie der Abstand von s zu v .
Wenn ein Knoten grün wird, garantiert die Relaxation, daß die
zweite Bedingung weiter gilt.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
Der Algorithmus von Dijkstra
Algorithmus
procedure Dijkstra(s) :
Q := V − {s};
for v ∈ Q do d[v ] := ∞ od;
d[s] := 0;
while Q 6= ∅ do
choose v ∈ Q with minimal d[v ];
Q := Q − {v };
forall u adjacent to v do
d[u] := min{d[u], d[v ] + length(v , u)}
od
od
Wie implementieren wir Q?
(Folie 310, Seite 77 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 311, Seite 77 im Skript)
Priority Queues (Prioritätswarteschlangen)
Operationen einer Prioritätswarteschlange Q:
1
2
3
Einfügen von x mit Gewicht w (insert)
Finden und Entfernen eines Elements mit minimalem Gewicht
(extract-min)
Das Gewicht eines Elements x auf w verringern
(decrease-weight)
5
9
22
17
11
25
Heap: alle Operationen in O(log n) Schritten
(n ist die aktuelle Anzahl von Elementen im Heap)
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 312, Seite 77 im Skript)
Algorithmus von Dijkstra – Laufzeit
Theorem
Der Algorithmus von Dijkstra berechnet die Abstände von s zu
allen anderen Knoten in O((|V | + |E |) log |V |) Schritten.
Beweis.
Es werden |V | Einfügeoperationen, |V | extract-mins und |E |
decrease-keys ausgeführt.
Verwenden wir einen Heap für die Prioritätswarteschlange, ergibt
sich die verlangte Laufzeit.
Ein Fibonacci-Heap benötigt für ein Einfügen und extract-min
O(log n) und für decrease-key nur O(1) amortisierte Zeit.
Dijkstra: O(|V | log |V | + |E |)
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 313, Seite 77 im Skript)
Java
public void dijkstra(Node s, MaphNode, Nodei pred) {
SimpleIterator hNodei it;
for(it = nodeiterator (); it.more(); it.step()) it.key ().weight = 1e10 ;
s.weight = 0.0;
HeaphNodei H = new HeaphNodei();
for(it = nodeiterator (); it.more(); it.step()) H.insert(it.key ());
while(!H.isempty ()) {
Node v = H.extract min();
Iterator hNode, Edgei inc;
for(inc = neighbors.find(v ).iterator (); inc.more(); inc.step())
if(inc.key ().weight > v .weight + inc.data().weight) {
pred.insert(inc.key (), v );
inc.key ().weight = v .weight + inc.data().weight;
H.decrease key (inc.key ());
}
}
}
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 314, Seite 77 im Skript)
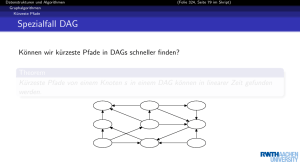
Spezialfall DAG
Können wir kürzeste Pfade in DAGs schneller finden?
Theorem
Kürzeste Pfade von einem Knoten s in einem DAG können in
linearer Zeit gefunden werden.
Beweis.
Relaxiere Knoten in topologischer Reihenfolge.
Laufzeit: O(|V | + |E |).
Korrektheit: Jeder Knoten, der relaxiert, kennt zu diesem
Zeitpunkt seinen echten Abstand.
Frage: Sind negative Gewichte hier erlaubt?
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 315, Seite 77 im Skript)
Kürzeste Wege mit negativen Kantengewichten
4
5
3
3
1
4
3
7
2
5
3
6
1
3
2
2
3
0
5
-4
3
5
4
∞
Dijkstra funktioniert nicht mit negativen Kantengewichten.
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
Der Algorithmus von Bellman und Ford
Idee:
Relaxiere alle Kanten
Wiederhole dies, bis keine Änderung
Warum korrekt?
Induktion über die Länge eines kürzesten Pfads.
(Also genügen n Wiederholungen)
Was passiert bei Kreisen mit negativem Gewicht?
→ Keine Terminierung.
(Folie 316, Seite 77 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
Der Algorithmus von Bellman und Ford
Algorithmus
function Bellman − Ford(s) boolean :
for v ∈ V do d[v ] := ∞ od;
d[s] := 0;
for i = 1 to|V | − 1 do
forall (u, v ) ∈ E do
d[u] := min{d[u], d[v ] + length(v , u)}
od
od;
forall (u, v ) ∈ E do
if d[u] > d[v ] + length(v , u) then return false fi
od;
return true
(Folie 317, Seite 77 im Skript)
Datenstrukturen und Algorithmen
Graphalgorithmen
Kürzeste Pfade
(Folie 318, Seite 77 im Skript)
Der Algorithmus von Bellman und Ford
Theorem
Gegeben sei ein gerichteter Graph G = (V , E ) mit
Kantengewichten E → R und ein Knoten s ∈ V .
Wir können in O(|V | · |E |) feststellen, ob ein Kreis mit negativem
Gewicht existiert, und falls nicht, die kürzesten Wege von s zu
allen Knoten berechnen.
Beweis.
Wir haben die Korrektheit bereits nachgewiesen.
Zur Laufzeit: Jeder Knoten wird |V | mal relaxiert, also wird auch
jede Kante |V | mal relaxiert (in konstanter Zeit).