Blatt04-Loesung - Institut für Informatik

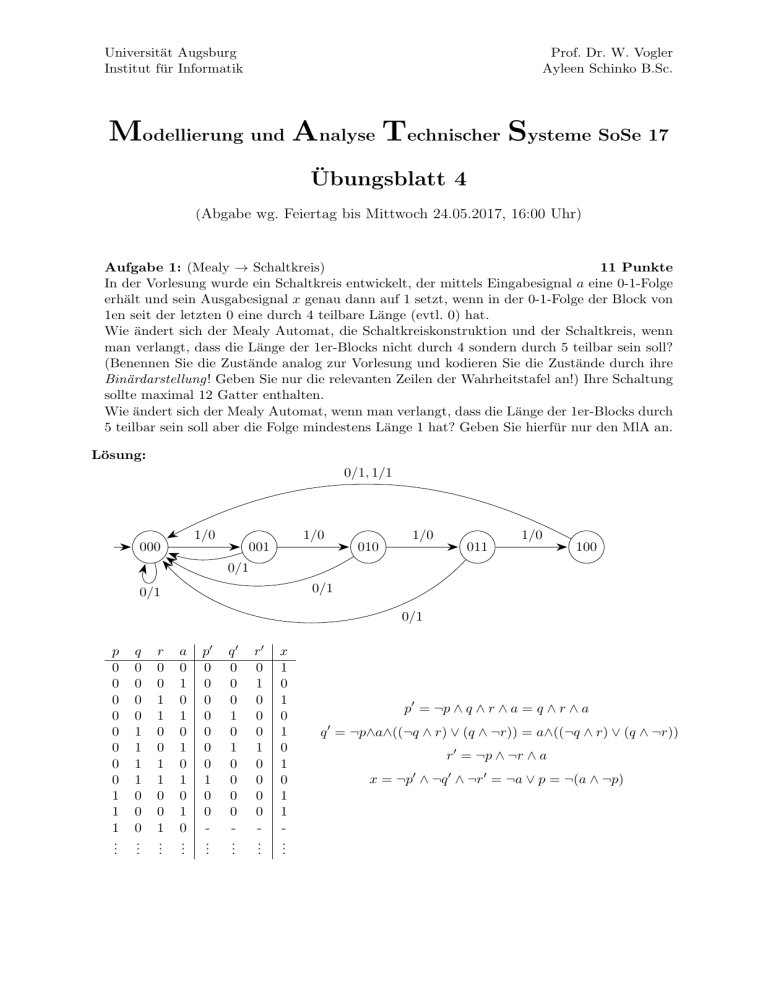
Universität Augsburg
Institut für Informatik
Prof. Dr. W. Vogler
Ayleen Schinko B.Sc.
Modellierung und Analyse Technischer Systeme SoSe 17
Übungsblatt 4
(Abgabe wg. Feiertag bis Mittwoch 24.05.2017, 16:00 Uhr)
Aufgabe 1: (Mealy → Schaltkreis)
11 Punkte
In der Vorlesung wurde ein Schaltkreis entwickelt, der mittels Eingabesignal a eine 0-1-Folge
erhält und sein Ausgabesignal x genau dann auf 1 setzt, wenn in der 0-1-Folge der Block von
1en seit der letzten 0 eine durch 4 teilbare Länge (evtl. 0) hat.
Wie ändert sich der Mealy Automat, die Schaltkreiskonstruktion und der Schaltkreis, wenn
man verlangt, dass die Länge der 1er-Blocks nicht durch 4 sondern durch 5 teilbar sein soll?
(Benennen Sie die Zustände analog zur Vorlesung und kodieren Sie die Zustände durch ihre
Binärdarstellung! Geben Sie nur die relevanten Zeilen der Wahrheitstafel an!) Ihre Schaltung
sollte maximal 12 Gatter enthalten.
Wie ändert sich der Mealy Automat, wenn man verlangt, dass die Länge der 1er-Blocks durch
5 teilbar sein soll aber die Folge mindestens Länge 1 hat? Geben Sie hierfür nur den MlA an.
Lösung:
0/1, 1/1
1/0
1/0
000
001
1/0
010
1/0
011
100
0/1
0/1
0/1
0/1
p
0
0
0
0
0
0
0
0
1
1
1
..
.
q
0
0
0
0
1
1
1
1
0
0
0
..
.
r
0
0
1
1
0
0
1
1
0
0
1
..
.
a
0
1
0
1
0
1
0
1
0
1
0
..
.
p0
0
0
0
0
0
0
0
1
0
0
..
.
q0
0
0
0
1
0
1
0
0
0
0
..
.
r0
0
1
0
0
0
1
0
0
0
0
..
.
x
1
0
1
0
1
0
1
0
1
1
..
.
p0 = ¬p ∧ q ∧ r ∧ a = q ∧ r ∧ a
q 0 = ¬p∧a∧((¬q ∧ r) ∨ (q ∧ ¬r)) = a∧((¬q ∧ r) ∨ (q ∧ ¬r))
r0 = ¬p ∧ ¬r ∧ a
x = ¬p0 ∧ ¬q 0 ∧ ¬r0 = ¬a ∨ p = ¬(a ∧ ¬p)
Übungsblatt 4 (Modellierung Technischer Systeme SoSe 17)
2
a
→
p
←
q
←
r
x
oder mit Vereinfachung von x (Vereinfachungen, dass man ¬p nicht berücksichtigen muss,
wurden nicht ausgeführt, da man das oberste UND-Gatter auf jeden Fall braucht):
Übungsblatt 4 (Modellierung Technischer Systeme SoSe 17)
3
a
→
p
←
q
←
r
x
Länge mindestens 1:
0/0, 1/1
1/0
000
1/0
001
1/0
010
1/0
011
100
0/0
0/0
0/0
0/0
Aufgabe 2: (bewerteter Term)
6 Punkte
Die Idee für die im folgenden auftretenden Terme ist, dass a, b für gerade Zahlen und c, d für
ungerade Zahlen stehen sollen; e und o sind einzelne Buchstaben.
Die Menge der bewerteten Terme bT ist die kleinste Menge mit
i) (a, e), (b, e), (c, o), (d, o) ∈ bT
ii) Seien (x, y), (x0 , y 0 ) ∈ bT .
a) Wenn entweder y = o oder y 0 = o, so auch ((x + x0 ), o) ∈ bT .
b) Andernfalls ((x + x0 ), e) ∈ bT .
iii) Seien (x, y), (x0 , y 0 ) ∈ bT .
a) Wenn y = e oder y 0 = e, so auch (x · x0 , e) ∈ bT .
b) Andernfalls (x · x0 , o) ∈ bT .
Bearbeiten Sie mit dieser Definition die folgenden Aufgaben:
Übungsblatt 4 (Modellierung Technischer Systeme SoSe 17)
4
1. Leiten sie mit den aufgeführten Regeln den bewerteten Term (((a · c + d) + d · c), e) ∈ bT
schrittweise her.
2. Was bedeutet es, wenn (x, e) ∈ bT bzw. (x, o) ∈ bT ? (Begründen Sie Ihre Aussage)
Lösung:
1. (1) (a, e), (b, e), (c, o), (d, o) ∈ bT , wegen i)
(2) (a · c, e) ∈ bT , wegen iii) a)
[mit (1)]
(3) (d · c, o) ∈ bT , wegen iii) b)
[mit (1)]
(4) ((a · c + d), o) ∈ bT , wegen ii) a)
[mit (2),(1)]
(5) (((a · c + d) + d · c), e) ∈ bT , wegen ii) b)
[mit (4),(3)]
2. (x, e) ∈ bT bedeutet, dass der Term x gerade ist, und (x, o) ∈ bT , dass der Term x
ungerade ist.
Begründung:
i) Für x = a, b, c, d gilt die Aussage aufgrund der angegebenen Idee.
ii) Die Addition zweier Zahlen ist genau dann ungerade, wenn genau eine der beiden
Zahlen ungerade ist.
iii) Die Multiplikation zweier Zahlen ist genau dann gerade, wenn mindestens einer der
beiden Faktoren gerade ist.
Aufgabe 3: (Schnitt regulärer Sprachen)
8 Punkte
1. Betrachten Sie die folgenden Automaten AQ und AP . Konstruieren Sie einen Automaten
A0 mit L(A0 ) = L(AP ) ∩ L(AQ ). Gehen Sie dabei nicht wie im Skript vor. Überlegen Sie
sich, wie die beiden Automaten gleichzeitig ein Wort lesen und akzeptieren. Konstruieren
Sie A0 systematisch auf Grundlage dieser Idee.
a
q1
a
AP
b
p1
b
b
AQ
p0
q0
a
q2
a
a
a, b
b
a
p2
p3
b
2. Seien nun A1 , A2 beliebige buchstabierende endliche Automaten über Σ. Geben Sie ein
direktes Konstruktionsverfahren für einen endlichen Automaten an, der L(A1 ) ∩ L(A2 )
entscheidet. ’Direkt’ bedeutet in diesem Fall unter anderem, dass Sie die Automaten
nicht zunächst deterministisch machen dürfen (Begrenzung der Zustandszahl).
Übungsblatt 4 (Modellierung Technischer Systeme SoSe 17)
Lösung:
5
1.
a
a
A0
q0 p 0
q2 p3
q1 p2
b
b
b
a
a
b
q2 p 2
a
q0 p2
a
a
b
q0 p3
2. Seien A1 = (Q1 , Σ, δ1 , q01 , F1 ) und A2 = (Q2 , Σ, δ2 , q02 , F2 ). Dann konstruieren wir
A = (Q, Σ, δ, q0 , F ) mit:
•
•
•
•
Q = Q1 × Q2
((q1 , q2 ), a, (p1 , p2 )) ∈ δ :⇔ (q1 , a, p1 ) ∈ δ1 ∧ (q2 , a, p2 ) ∈ δ2 für alle a ∈ Σ
q0 = (q01 , q02 )
F = F1 × F2