Mathematik IV (Stochastik) für Informatiker

Bausteine zur Vorlesung von Prof. Dr. Bernd Hofmann
Mathematik IV (Stochastik) für Informatiker
Fakultät für Mathematik der Technischen Universität Chemnitz
Sommersemester 2017
Dieser Text soll die Nacharbeit der Vorlesung erleichern und an Definitionen, Sätze, Zusammenhänge und Beispiele erinnern. Hinweise zu
Tippfehlern und Unstimmigkeiten werden gern entgegengenommen.
Textstand: 20.06.2017.
2
Inhaltsverzeichnis
1 Einführung in die Wahrscheinlichkeitsrechnung
1.1
1.2
1.3
1.4
1.5
5
Wahrscheinlichkeitsräume . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.1.1
Rechnen mit zufälligen Ereignissen . . . . . . . . . . . . . . . . . . . . .
6
1.1.2
Rechnen mit Wahrscheinlichkeiten . . . . . . . . . . . . . . . . . . . . .
8
1.1.3
Grundformeln der Kombinatorik . . . . . . . . . . . . . . . . . . . . . .
10
Bedingte Wahrscheinlichkeiten
. . . . . . . . . . . . . . . . . . . . . . . . . . .
11
1.2.1
Multiplikationsregel, totale Wahrscheinlichkeit, Satz von Bayes . . . . .
12
1.2.2
Stochastische Unabhängigkeit zufälliger Ereignisse . . . . . . . . . . . .
14
1.2.3
Methode der geometrischen Wahrscheinlichkeit . . . . . . . . . . . . . .
16
1.2.4
Ergänzende Beispiele zur Einführung von Wahrscheinlichkeiten . . . . .
16
Zufallsgrößen und Verteilungsfunktionen . . . . . . . . . . . . . . . . . . . . . .
19
1.3.1
Einführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
1.3.2
Diskrete Zufallsgrößen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
1.3.3
Stetige Zufallsgrößen . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
31
Das Gesetz der großen Zahlen und Grenzverteilungssätze . . . . . . . . . . . . .
43
1.4.1
Das Gesetz der großen Zahlen . . . . . . . . . . . . . . . . . . . . . . . .
43
1.4.2
Grenzverteilungssätze . . . . . . . . . . . . . . . . . . . . . . . . . . . .
44
Mehrdimensionale Verteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
1.5.1
Einführung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
48
1.5.2
Bedingte Verteilungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
53
1.5.3
Erwartungswertevektor, Kovarianzmatrix, Normalverteilung . . . . . . .
54
2 Einführung in die mathematische Statistik
56
2.1
Grundbegriffe . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
56
2.2
Punktschätzung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
57
2.3
Verteilungen wichtiger Stichprobenfunktionen . . . . . . . . . . . . . . . . . . .
59
2.3.1
Quantile . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
59
2.3.2
Weitere stetige Verteilungen . . . . . . . . . . . . . . . . . . . . . . . . .
60
2.3.3
Stichprobenfunktionen bei binomialverteilter Grundgesamtheit . . . . .
62
3
2.3.4
2.4
2.5
2.6
Stichprobenfunktionen bei normalverteilter Grundgesamtheit . . . . . .
62
Bereichsschätzung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
63
2.4.1
Konfidenzintervalle bei binomialverteilter Grundgesamtheit . . . . . . .
63
2.4.2
Konfidenzintervalle bei normalverteilter Grundgesamtheit . . . . . . . .
64
2.4.3
Einseitige Konfidenzintervalle . . . . . . . . . . . . . . . . . . . . . . . .
66
Tests . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
66
2.5.1
Allgemeines Schema für Parametertests . . . . . . . . . . . . . . . . . .
66
2.5.2
Parametertests bei binomialverteilter Grundgesamtheit . . . . . . . . . .
67
2.5.3
Parametertests bei normalverteilter Grundgesamtheit . . . . . . . . . . .
68
2.5.4
Vergleich zweier normalverteilter Grundgesamtheiten . . . . . . . . . . .
71
2.5.5
χ2 -Test . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
72
Spezielle Schätzverfahren . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
73
2.6.1
Maximum-Likelihood-Methode . . . . . . . . . . . . . . . . . . . . . . .
73
2.6.2
Momentenmethode . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
75
2.6.3
Methode der kleinsten Quadrate . . . . . . . . . . . . . . . . . . . . . .
76
4
1 Einführung in die
Wahrscheinlichkeitsrechnung
Ziel dieses Kapitels ist die Einführung in mathematische Modelle zur Behandlung von zufallsbeeinflussten Vorgängen (Zufallssituationen). Dazu betrachten wir zunächst zwei einfache
Beispiele.
Beispiel (Geburtstagsaufgabe). In einem Raum befinden sich n Personen. Wie groß ist die
Wahrscheinlichkeit, dass mindestens zwei der n Personen am selben Tag Geburtstag haben?
Wie muss n gewählt werden, damit die Wahrscheinlichkeit dafür größer als 12 ist? Wir werden
diese Aufgabe in Abschnitt 1.1.3 lösen.
Beispiel. Zwei Personen A und B spielen mehrere Runden eines Spiels mit Geldeinsatz, bei
dem jeder Spieler gleiche Gewinnchancen hat. Gesamtsieger ist, wer zuerst 4 Siege erreicht. Bei
einem Stand von 3 : 1 für A wird das Spiel abgebrochen und die beiden Spieler teilen das Geld
anhand der Wahrscheinlichkeit eines Gesamtsieges unter sich auf. Wie viel bekommt jeder?
Lösung: Um Gesamtsieger zu werden, müsste B die nächsten 3 Spiele gewinnen: 12 · 12 · 12 = 18 .
In allen anderen Fällen gewinnt A als erster 4 Spiele. Somit erhält Spieler A 87 und Spieler B
1
8 des Einsatzes.
Anwendung der Wahrscheinlichkeitsrechnung
• Statistische Qualitätskontrolle,
• Fehlerrechnung,
• Versicherungswesen,
• stochastische Finanzmathematik.
1.1 Wahrscheinlichkeitsräume
Zufallssituation: Eine Zufallssituation ist dadurch gekennzeichnet, dass sie (zumindest gedanklich) beliebig oft wiederholbar ist und das Ergebnis absolut nicht vorhersagbar ist.
Wahrscheinlichkeitsraum: Ein Wahrscheinlichkeitsraum ist die Zusammenfassung aller Teile
eines mathematischen Modells zur Beschreibung einer Zufallssituation. Verschiedene Zufallssituationen führen im Allgemeinen auch auf verschiedene Wahrscheinlichkeitsräume.
Versuch: Ein Versuch ist die Realisierung einer Zufallssituation.
Mit Ω bezeichnen wir die Ergebnismenge eines Versuchs, d.h. die Menge aller möglichen
Ergebnisse, und mit ω ein konkretes Ergebnis, also ω ∈ Ω. Dabei gehen wir davon aus, dass
jedem Ergebnis eines Versuchs eindeutig ein Element ω der Ergebnismenge Ω zugeordnet ist.
5
Beispiel. Beim Werfen eines idealen Würfels ist Ω = {1, 2, 3, 4, 5, 6} eine endliche Ergebnismenge mit 6 möglichen verschiedenen Ergebnissen.
Beispiel. Ein Fahrzeug kann mit einem begrenzten Treibstoffvorrat nur eine bestimmte Strecke
zurücklegen. Somit ist Ω = {ω ∈ R : ω ≥ 0} eine überabzählbar unendliche Ergebnismenge.
Beispiel. Es soll der Zustand von n elektrischen Geräten überprüft werden. Wir bezeichnen
den Zustand des i-ten Gerätes mit
{
1, Gerät in Ordnung
ωi =
.
0, Gerät defekt
{
}
Somit ist Ω = (ω1 , . . . , ωn ) ∈ Rn : ωi ∈ {0, 1} eine endliche Ergebnismenge mit n Elementen.
Beispiel. Bei der Bestimmung der Lebensdauer von n Lampen, wobei ωi die Lebensdauer der
i-ten Lampe bezeichnet, ist die Ergebnismenge Ω = {(ω1 , . . . , ωn ) ∈ Rn : ωi ≥ 0} überabzählbar
unendlich.
Definition 1.1.1. Ein zufälliges Ereignis ist eine Teilmenge A ⊂ Ω der Ergebnismenge. Man
sagt, dass das Ereignis A eingetreten ist, wenn das Versuchsergebnis ω in A liegt, d.h. wenn
ω ∈ A gilt.
Nicht jede Teilmenge A ⊂ Ω muss sich als zufälliges Ereignis betrachten lassen, aber alle
zufälligen Ereignisse sind Teilmengen von Ω.
Beispiel. Wir betrachten beim Würfeln mit einem idealen Würfel das Ereignis „gerade Zahl
gewürfelt“. Haben also A = {2, 4, 6}.
Beispiel. Für ein Fahrzeug mit begrenztem Treibstoffvorrat interessiert das Ereignis „fährt
mindestens 150 km“. Haben dann A = {ω ∈ R : ω ≥ 150}.
Beispiel. Bei der Überprüfung von n Geräten sollen „mindestens 2 in Ordnung“ sein, d.h.
A = {(ω1 , . . . , ωn ) ∈ Rn : ωi ∈ {0, 1} und ω1 + . . . + ωn ≥ 2}.
Beispiel. Die mittlere Brenndauer von n Lampen soll „zwischen 500 und 5000 Stunden“ ben
tragen, d.h. A = {(ω1 , . . . , ωn ) ∈ Rn : 500 ≤ ω1 +...+ω
≤ 5000}.
n
1.1.1 Rechnen mit zufälligen Ereignissen
Oder-Ereignis: Das Ereignis C = „A oder B“ tritt ein, wenn entweder A oder B oder beide
eintreten, d.h. C = A ∪ B.
Und-Ereignis: Das Ereignis C = „A und B“ tritt ein, wenn sowohl A als auch B eintritt, d.h.
C = A ∩ B.
Komplementärereignis (Gegenereignis): Das Ereignis C = A = „nicht A“ tritt ein, wenn A
nicht eintritt, d.h. C = Ω \ A.
Sicheres Ereignis: A = Ω.
Unmögliches Ereignis: A = Ω = ∅.
Elementarereignis: A = {ω}, d.h. A enthält genau ein Element der Ergebnismenge Ω.
6
Unvereinbare Ereignisse: A und B heißen unvereinbar, wenn A ∩ B = ∅ gilt.
Man kann „oder“ und „und“ auch auf endlich bzw. abzählbar unendlich viele Ereignisse anwenden:
n
n
∞
∞
∪
∩
∪
∩
Ai und
Ai
bzw.
Ai und
Ai .
i=1
i=1
i=1
i=1
Definition 1.1.2. Eine Menge A von Ereignissen, d.h. von Teilmengen der Ergebnismenge Ω,
heißt bezogen auf eine feste Zufallssituation Ereignisfeld (auch Ereignisalgebra oder σ-Algebra),
wenn die folgenden drei Bedingungen erfüllt sind:
• Ω∈A
(sicheres Ereignis gehört dazu),
• A ∈ A ⇒ A ∈ A ∀A ∈ A
• A1 , A2 , . . . ∈ A ⇒
∞
∪
(mit Ereignis gehört auch Komplementärereignis dazu),
Ai ∈ A ∀A1 , A2 , . . . ∈ A
(abzählbare Vereinigungen ebenfalls).
i=1
Satz 1.1.3 (Rechenregeln). Für zufällige Ereignisse A und B bzw. A1 , A2 , . . . gilt:
•
A∪B =B∪A
(Kommutativität),
A∩B =B∩A
•
(A ∪ B) ∪ C = A ∪ (B ∪ C)
(Assoziativität),
(A ∩ B) ∩ C = A ∩ (B ∩ C)
•
(A ∪ B) ∩ C = (A ∩ C) ∪ (B ∩ C)
(Distributivität),
(A ∩ B) ∪ C = (A ∪ C) ∩ (B ∪ C)
•
A∪B =A∩B
( De Morgan’sche Regeln),
A∩B =A∪B
n
∪
•
i=1
n
∩
Ai =
Ai =
i=1
n
∩
i=1
n
∪
Ai ,
Ai ,
i=1
∞
∪
i=1
∞
∩
∞
∩
Ai =
Ai =
i=1
• A ∪ ∅ = A,
A ∩ ∅ = ∅,
• A ∪ Ω = Ω,
A ∩ Ω = A.
i=1
∞
∪
Ai
(verallgemeinerte De Morgan’sche Regeln),
Ai
i=1
Falls ω ∈ A ⇒ ω ∈ B für alle ω ∈ A gilt, so sagen wir „A zieht B nach sich“ und schreiben
A ⊂ B. Dazu äquivalente mathematische Beschreibungen sind
A⊂B
⇔
A∩B =A
⇔
A∪B =B
⇔
A∩B =∅
⇔
Venn-Diagramme sind hilfreich bei der Illustration des Ereignis-Kalküls!
7
B ⊂ A.
1.1.2 Rechnen mit Wahrscheinlichkeiten
Definition 1.1.4. Sei A ∈ A ein festes Ereignis innerhalb einer Zufallssituation. Wir Bezeichnen dann mit n die Anzahl der ausgeführten Versuche, mit nA die Anzahl der Versuche, bei
denen A eingetreten ist, und mit
nA
Hn = Hn (A) =
n
die relative Häufigkeit für das Eintreten von A bei n Versuchen. Erfahrungsgemäß strebt Hn (A)
unter Verwendung eines speziell zugeschnittenen Grenzwertbegriffs gegen eine feste Zahl, die
Wahrscheinlichkeit P (A) für das Eintreten von A:
P (A) = lim Hn (A).
n→∞
Beispiel. Beim Werfen einer Münze wird das Ereignis A = „Kopf liegt oben“ betrachtet. Schon
in den vergangenen Jahrhunderten galten Münzexperimente als interessant. Sie wurden z.B. von
Comte de Buffon (1707-1788) und K. Pearson (1857-1936) durchgeführt.
Buffon
Pearson
n
4040
24000
nA
2048
12012
Hn (A)
0,5069
0,5005
P (A)
0,5
0,5
Eigenschaften der relativen Häufigkeit
• Offenbar ist 0 ≤ Hn (A) ≤ 1.
• Ebenfalls offenbar ist Hn (Ω) = 1.
• Für unvereinbare Ereignisse A und B, d.h. A∩B = ∅, addieren sich offenbar die relativen
Häufigkeiten:
Hn (A ∪ B) =
nA + nB
nA nB
nA∪B
=
=
+
= Hn (A) + Hn (B).
n
n
n
n
Diese Eigenschaften der relativen Häufigkeit bilden die Grundlage des Axiomensystems zum
Rechnen mit Wahrscheinlichkeiten nach Kolmogorov (veröffentlicht 1933 im Springer-Verlag
in seinem in deutscher Sprache verfassten Buch Grundbegriffe der Wahrscheinlichkeitsrechnung).
Definition 1.1.5 (Kolmogorov’sches Axiomensystem). Gegeben sei eine Zufallssituation,
die durch eine Ergebnismenge Ω und ein Ereignisfeld A beschrieben wird. Jedem A ∈ A ist dann
eindeutig eine reelle Zahl P (A), die Wahrscheinlichkeit für das Eintreten von A, zugeordnet.
Dabei gelten die folgenden Axiome.
A1: Es gelte 0 ≤ P (A) ≤ 1.
A2: Es gelte P (Ω) = 1.
A3: Für paarweise unvereinbare Ereignisse Ai ∈ A, d.h. Ai ∩ Aj = ∅ mit i ̸= j gelte stets
(∞ )
∞
∪
∑
P
Ai =
P (Ai ).
i=1
i=1
8
Folgerungen aus den Kolmogorov’schen Axiomen Für beliebige Ereignisse A, B ∈ A
gilt:
• P (∅) = 0.
Beweis. Seien A1 = ∅ und A2 = ∅ unvereinbare Ereignisse (A1 ∩ A2 = ∅). Haben dann
unter Verwendung von A1 ∪ A2 = ∅ und Axiom A3
P (A1 ∪ A2 ) = P (A1 ) + P (A2 )
⇒
P (∅) = 2P (∅) = 0.
• P (A) = 1 − P (A).
Beweis. Es gilt A ∪ A = Ω und A ∩ A = ∅. Axiom A3 liefert also P (Ω) = P (A) + P (A)
und aus Axiom A2 folgt somit 1 = P (A) + P (A).
• P (A ∩ B) = P (A) − P (A ∩ B).
Beweis. Es gilt A = A ∩ Ω = A ∩ (B ∪ B) = (A ∩ B) ∪ (A ∩ B). Aus Axiom A3 folgt
somit P (A) = P (A ∩ B) + P (A ∩ B).
• P (A ∪ B) = P (A) + P (B) − P (A ∩ B).
Beweis. Es gilt A ∪ B = (A ∩ B) ∪ B = (A ∩ A ∩ B) ∪ B und somit ist nach dem
vorhergehenden Punkt und Axiom A3
P (A ∪ B) = P (A ∩ A ∩ B) + P (B) = P (A) − P (A ∩ B) + P (B).
Methode der klassischen Wahrscheinlichkeit Für eine endliche Ergebnismenge Ω mit N
Elementen ω1 , . . . , ωN und
P ({ω1 }) = · · · = P ({ωN }) =
1
N
(Laplace-Annahme)
gilt mit A = {ωi1 , . . . , ωiM }
P (A) =
M
Anzahl der günstigen Fälle
=
.
N
Anzahl der möglichen Fälle
Beispiel. Beim Würfeln mit einem idealen Würfel wird das Ereignis A = „Primzahl gewürfelt“
betrachtet. Haben dann A = {2, 3, 5}, M = 3, N = 6 und somit P (A) = 36 = 12 .
Definition 1.1.6. Durch die Ergebnismenge Ω, das Ereignisfeld A und das Wahrscheinlichkeitsmaß P sei eine Zufallssituation gegeben. Das Tripel (Ω, A, P ) heißt Wahrscheinlichkeitsraum
dieser Zufallssituation.
9
1.1.3 Grundformeln der Kombinatorik
Aus einem Gefäß mit n Kugeln, die (z.B. durch Nummerierung) unterscheidbar sind, sollen
m Kugeln entnommen werden. Uns interessiert die Anzahl der möglichen Ergebnisse. Dabei
berücksichtigen wir, ob die Reihenfolge eine Rolle spielt und ob eine entnommene Kugel vor
der Entnahme der nächsten wieder zurückgelegt wird.
• Variationen (Reihenfolge wichtig):
m
Anzahl mit Zurücklegen1 = w V m
n =n ,
Anzahl ohne Zurücklegen = Vnm = n(n − 1)(n − 2) . . . (n − m + 1) =
• Kombinationen (Reihenfolge unwichtig):
Anzahl mit Zurücklegen = w C m
n =
Anzahl ohne Zurücklegen = Cnm =
(n+m−1)
m
(n)
m
=
n!
(n−m)! .
,
n!
m!(n−m)! .
Beispiel. In einem Raum befinden sich n Personen, von denen keine am 29. Februar Geburtstag
hat. An sei das Ereignis, dass mindestens 2 der n Personen am gleichen Tag Geburtstag haben,
wobei wir davon ausgehen, dass alle 365 möglichen Tage gleichwahrscheinlich sind. Wir betrachten An und berechnen dann P (An ) durch P (An ) = 1 − P (An ). Wir ziehen unter Beachtung der
Reihenfolge und mit Zurücklegen n Tage aus 365 und erhalten somit N = 365n mögliche Fälle.
Ziehen von n Tagen aus 365 ohne Zurücklegen und unter Beachtung der Reihenfolge ergibt
M = 365 · 364 · . . . · (365 − n + 1) günstige Ergebnisse. Haben somit
P (An ) =
M
365 · 364 · . . . · (366 − n)
=
.
N
365n
Für konkrete n erhalten wir die folgenden Wahrscheinlichkeiten.
n
1
2
3
4
5
10
P (An )
0
0,003
0,008
0,016
0,027
0,117
n
15
20
22
23
30
40
P (An )
0,253
0,411
0,476
0,507
0,706
0,891
n
50
60
70
80
90
100
P (An )
0,970
0,9941
0,99916
0,999914
0,9999938
0,99999969
Ab n = 23 Personen im Raum ist die Wahrscheinlichkeit, dass zwei am gleichen Tag Geburtstag
haben, also größer als 50 %.
Beispiel. Es werden 6 aus 49 nummerierten Kugeln ohne Zurücklegen und ohne Beachtung der
Reihenfolge gezogen. Zuvor wird ein Tipp abgegeben, welche Kugeln dies sein werden. Ak mit
k = 0, . . . , 6 bezeichne das Ereignis, dass genau k Kugeln richtig getippt wurden. Wir erhalten
(6)( 43 )
(6)( 43 )
günstige Fälle
k 6−k
P (Ak ) =
= (49) = k 6−k .
mögliche Fälle
13983816
6
Dies ergibt die folgenden Wahrscheinlichkeiten.
1
w steht für „mit Wiederholung“
10
k
0
1
2
3
günstige Fälle
6096454
5775588
1851150
246820
P (Ak )
0,436
0,413
0,132
0,018
günstige Fälle
13545
258
1
k
4
5
6
P (Ak )
0,0009686
0,00001845
0,000000072
1.2 Bedingte Wahrscheinlichkeiten
In bestimmten Zufallssituationen kann es vorkommen, dass sich die Wahrscheinlichkeit für
das Eintreten eines Ereignisses ändert, wenn man beachtet, dass ein anderes Ereignis bereits
eingetreten ist.
Als Motivation für die Einführung bedingter Wahrscheinlichkeiten betrachten wir die relative
Häufigkeit: Es werden n Versuche durchgeführt. Die relative Häufigkeit für das Eintreten von
Ereignis A als Folge des Eintretens von B berechnet sich durch
nA∩B
Hn (A|B) :=
=
nB
nA∩B
n
nB
n
=
Hn (A ∩ B)
.
Hn (B)
Definition 1.2.1. Sei (Ω, A, P ) ein Wahrscheinlichkeitsraum und seien A und B zwei zufällige
Ereignisse mit P (B) > 0. Dann heißt die Größe
P (A|B) :=
P (A ∩ B)
P (B)
bedingte Wahrscheinlichkeit für das Eintreten von Ereignis A unter der Bedingung, dass B
bereits eingetreten ist.
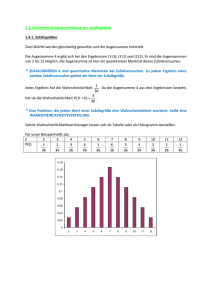
Beispiel. Mit einem idealen Würfel werden zwei Würfe ausgeführt. Wir betrachten die beiden
Ereignisse
A = „erster Wurf ist eine 6“ = {(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (6, 6)},
B = „Augensumme beider Würfe ist 8“ = {(6, 2), (5, 3), (4, 4), (3, 5), (2, 6)}.
Offensichtlich ist P (A) =
6
36
= 16 , P (B) =
5
36
und P (A ∩ B) =
1
36 .
Somit ist P (A|B) = 15 .
Rechenregeln für bedingte Wahrscheinlichkeiten
• P (A|C) = 1 − P (A|C).
Beweis.
P (A ∩ C) P (A ∩ C)
+
P (C)
P (C)
P ((A ∩ C) ∪ (A ∩ C))
P ((A ∪ A) ∩ (A ∪ C) ∩ (C ∪ A) ∩ (C ∪ C))
=
P (C)
P (C)
P (Ω ∩ (A ∪ C) ∩ (C ∪ A) ∩ C)
P (Ω ∩ C ∩ C)
P (C)
=
=
= 1.
P (C)
P (C)
P (C)
P (A|C) + P (A|C) =
=
=
11
• P (A ∪ B|C) = P (A|C) + P (B|C) − P (A ∩ B|C).
Beweis.
P ((A ∪ B) ∩ C)
P ((A ∩ C) ∪ (B ∩ C))
=
P (C)
P (C)
P (A ∩ C) + P (B ∩ C) − P (A ∩ B ∩ C)
=
P (C)
P (A ∩ C) P (B ∩ C) P ((A ∩ B) ∩ C)
=
+
−
P (C)
P (C)
P (C)
= P (A|C) + P (B|C) − P (A ∩ B|C).
P (A ∪ B|C) =
• P (C|C) = 1
Beweis.
P (C|C) =
P (C ∩ C)
P (C)
=
= 1.
P (C)
P (C)
Beispiel. Torsten durchsucht 7 gleichgroße CD-Stapel nach einer ganz bestimmten CD. Die
Wahrscheinlichkeit, dass die gesuchte CD überhaupt in einem der Stapel vorhanden ist, sei
4
5 . Er hat bereits 6 Stapel erfolglos durchsucht. Wie groß ist die Wahrscheinlichkeit, die CD
im 7. Stapel zu finden? Ai mit i = 1, . . . , 7 sei das Ereignis „CD im i-ten Stapel“, wobei
P (A1 ) = . . . = P (A7 ). Haben dann
1
1
1 4
4
P (Ai ) = (P (A1 ) + . . . + P (A7 )) = P (A1 ∪ . . . ∪ A7 ) = · =
7
7
7 5
35
und somit
P (A7 |A1 ∩ . . . ∩ A6 ) =
4
P (A7 ∩ A1 ∩ . . . ∩ A6 )
P (A7 )
35
=
=
1 − P (A1 ∪ . . . ∪ A6 )
1−6·
P (A1 ∩ . . . ∩ A6 )
4
35
=
4
.
11
1.2.1 Multiplikationsregel, totale Wahrscheinlichkeit, Satz von Bayes
Stellt man die Formel für die bedingte Wahrscheinlichkeit P (A|B) (siehe Definition 1.2.1) nach
P (A∩B) um, so erhält man die einfache Multiplikationsregel :
P (A ∩ B) = P (A|B)P (B) = P (B|A)P (A).
Beispiel. An einer Universität schließen 70 % eines Jahrgangs das Fach Mathematik wenigstens
mit der Note 3 ab (Ereignis B). Unter diesen Studenten erreichen 25 % sogar eine der Noten 1
oder 2 (Ereignis A). Mit welcher Wahrscheinlichkeit schließt ein beliebig ausgewählter Student
7
des Jahrgangs das Fach mit 1 oder 2 ab? Lösung: Mit P (B) = 10
und P (A|B) = 14 liefert die
Multiplikationsregel
P (A) = P (A ∩ B) = P (A|B)P (B) =
12
1 7
7
·
=
= 0,175.
4 10
40
Satz 1.2.2 (erweiterte Multiplikationsregel). Seien A1 , A2 , . . . , An Ereignisse aus dem Ereignisfeld A einer festen Zufallssituation mit P (A1 ∩ A2 ∩ . . . ∩ An−1 ) > 0. Dann gilt
P (A1 ∩ A2 ∩ . . . ∩ An ) = P (A1 )P (A2 |A1 )P (A3 |A1 ∩ A2 ) · · · P (An |A1 ∩ A2 ∩ . . . ∩ An−1 ).
Beweis. Der Satz folgt durch vollständige Induktion aus der einfachen Multiplikationsregel:
P (A1 ∩ . . . ∩ An ) = P (An |A1 ∩ . . . ∩ An−1 )P (A1 ∩ . . . ∩ An−1 )
P (A1 ∩ . . . ∩ An−1 ) = P (An−1 |A1 ∩ . . . ∩ An−2 )P (A1 ∩ . . . ∩ An−2 )
..
.
P (A1 ∩ A2 ∩ A3 ) = P (A3 |A1 ∩ A2 )P (A1 ∩ A2 )
P (A1 ∩ A2 ) = P (A2 |A1 )P (A1 ).
Definition 1.2.3. Eine Menge von Ereignissen B1 , B2 , . . . , Bn heißt vollständiges Ereignissystem, wenn gilt:
• B1 ∪ B2 ∪ . . . ∪ Bn =
n
∪
Bi = Ω,
i=1
• die Ereignisse sind paarweise unvereinbar (disjunkt), d.h. Bi ∩ Bj = ∅ für i ̸= j.
Satz 1.2.4 (Satz von der totalen Wahrscheinlichkeit). Sei die Menge der Ereignisse B1 , . . . , Bn
ein vollständiges Ereignissystem. Dann gilt für ein beliebiges (anderes) Ereignis A die Formel
P (A) =
n
∑
P (A|Bi )P (Bi ).
i=1
Beweis. Es gilt
A = A ∩ Ω = A ∩ (B1 ∪ . . . ∪ Bn ) = (A ∩ B1 ) ∪ . . . ∪ (A ∩ Bn )
und da die Ereignisse A ∩ Bi (i = 1, . . . , n) paarweise unvereinbar sind, können wir die Multiplikationsregel anwenden und erhalten
P (A) = P ((A ∩ B1 ) ∪ . . . ∪ (A ∩ Bn )) =
n
∑
P (A ∩ Bi ) =
i=1
n
∑
P (A|Bi )P (Bi ).
i=1
Satz 1.2.5 (Satz von Bayes). Sei die Menge der Ereignisse B1 , . . . , Bn ein vollständiges Ereignissystem. Dann gilt für ein beliebiges (anderes) Ereignis A mit P (A) > 0 und für j = 1, . . . , n
die Formel
P (Bj |A) =
P (A|Bj )P (Bj )
P (A|Bj )P (Bj )
= ∑n
P (A)
i=1 P (A|Bi )P (Bi )
( Bayes’sche Formel).
Beweis. Der Satz ist eine direkte Folgerung aus der Multiplikationsregel und aus dem Satz von
13
der totalen Wahrscheinlichkeit:
P (A ∩ Bj ) = P (A|Bj )P (Bj ) = P (Bj |A)P (A)
⇒
P (Bj |A) =
P (A|Bj )P (Bj )
.
P (A)
Beispiel. Aus der Jahresstatistik einer großen deutschen Pannenhilfsorganisation geht hervor,
dass bei vorgefundenen Schäden im Bereich der Motorausfälle die folgende Schadenstypenverteilung zu verzeichnen war:
• 50 % Störungen der Zündanlage (davon 50 % vor Ort behoben),
• 30 % Störungen der Kraftstoffzufuhr (davon 30 % vor Ort behoben),
• 20 % sonstige Störungen (davon 5 % vor Ort behoben).
Uns interessiert nun, wie viel Prozent der Motorausfälle vor Ort behoben werden konnten und
wie sich die vor Ort behobenen Motorausfälle auf die einzelnen Schadensarten verteilen.
Wir bezeichnen die Ereignisse einer Störung mit B1 (Zündanlage), B2 (Kraftstoffzufuhr)
und B3 (sonstige Störungen) und das Ereignis, dass ein Motorausfall vor Ort behoben werden
konnte mit A. Die Ereignisse B1 , B2 , B3 bilden ein vollständiges Ereignissystem. Aus dem Satz
von der totalen Wahrscheinlichkeit erhalten wir
P (A) = P (A|B1 ) P (B1 ) + P (A|B2 ) P (B2 ) + P (A|B3 ) P (B3 ) = 0,35,
| {z } | {z } | {z } | {z } | {z } | {z }
0,5
0,5
0,3
0,3
0,05
0,2
d.h. in 35 % aller Fälle konnte vor Ort geholfen werden. Die Aufteilung der vor Ort behobenen
Motorausfälle auf die einzelnen Schadensarten erhalten wir mit dem Satz von Bayes:
P (A|B1 )P (B1 )
= 0,714,
P (A)
P (A|B2 )P (B2 )
P (B2 |A) =
= 0,257,
P (A)
P (A|B3 )P (B3 )
= 0,029.
P (B3 |A) =
P (A)
P (B1 |A) =
1.2.2 Stochastische Unabhängigkeit zufälliger Ereignisse
Definition 1.2.6. Zwei Ereignisse A, B ∈ A heißen stochastisch unabhängig, wenn gilt
P (A ∩ B) = P (A)P (B).
Bemerkung. „Stochastisch unabhängig“ bedeutet also P (A|B) = P (A) und P (B|A) = P (B),
d.h. der Zufallscharakter der Ereignisse A und B beeinflusst sich nicht.
Satz 1.2.7. Wenn die Ereignisse A und B stochastisch unabhängig sind, so sind auch die
Ereignisse A und B stochastisch unabhängig.
Beweis. Es gilt
P (A ∩ B) = P (A) − P (A ∩ B) = P (A) − P (A)P (B) = P (A)(1 − P (B)) = P (A)P (B),
14
d.h. A und B sind stochastisch unabhängig, woraus analog die stochastische Unabhängigkeit
von A und B folgt.
Beispiel. Ein elektrisches Gerät besteht aus zwei Bauteilen T1 und T2 , bei denen unabhängig
voneinander Defekte auftreten können. Wir betrachten die stochastisch unabhängigen Ereignisse A1 = „Bauteil T1 funktioniert“ mit P (A1 ) = p1 und A2 = „Bauteil T2 funktioniert“ mit
P (A2 ) = p2 .
Eine Serienschaltung der beiden Bauteile funktioniert, wenn sowohl T1 als auch T2 funktioniert:
P (A1 ∩ A2 ) = P (A1 )P (A2 ) = p1 p2 .
Für das Zahlenbeispiel p1 = p2 = 0,9 ergibt dies eine Wahrscheinlichkeit für das Funktionieren
des Geräts von 0,81.
Eine Parallelschaltung funktioniert, wenn T1 oder T2 oder beide funktionieren:
P (A1 ∪ A2 ) = 1 − P (A1 ∪ A2 ) = 1 − P (A1 ∩ A2 ) = 1 − (1 − p1 )(1 − p2 ).
Für das Zahlenbeispiel p1 = p2 = 0,9 ergibt dies eine Wahrscheinlichkeit für das Funktionieren
des Geräts von 0,99.
Definition 1.2.8. Die Ereignisse A1 , . . . , An heißen vollständig stochastisch unabhängig, wenn
für jede Auswahl von k Ereignissen aus den n gegebenen gilt:
P (Ai1 ∩ Ai2 ∩ . . . ∩ Aik ) = P (Ai1 )P (Ai2 ) · · · P (Aik ).
Aus dieser Definition ergibt sich für vollständig stochastisch unabhängige Ereignisse der
folgende wichtige Zusammenhang:
P (A1 ∪ · · · ∪ An ) = 1 − P (A1 ∪ · · · ∪ An ) = 1 − P (A1 ∩ · · · ∩ An )
= 1 − (1 − P (A1 )) · · · (1 − P (An )).
Beispiel. Paarweise stochastisch unabhängige Ereignisse müssen nicht gleichzeitig vollständig
stochastisch unabhängig sein. Sei z.B. Ω = {1, 2, 3, 4} mit
P ({1}) = P ({2}) = P ({3}) = P ({4}) =
Dann ist P (A) = P (B) = P (C) =
1
2
1
4
und A = {1, 2}, B = {1, 3}, C = {2, 3}.
und
1
= P (A)P (B),
4
1
P (A ∩ C) = P ({2}) = = P (A)P (C),
4
1
P (B ∩ C) = P ({3}) = = P (B)P (C).
4
P (A ∩ B) = P ({1}) =
Also sind die Ereignisse A, B, C paarweise stochastisch unabhängig, aber
P (A ∩ B ∩ C) = P (∅) = 0 ̸=
1
= P (A)P (B)P (C),
8
d.h. die Ereignisse A, B, C sind nicht vollständig stochastisch unabhängig.
15
1.2.3 Methode der geometrischen Wahrscheinlichkeit
Die Methode der geometrischen Wahrscheinlichkeit ist ein Spezialfall der klassischen Wahrscheinlichkeit (siehe Abschnitt 1.1.2). Die Ergebnismenge Ω ist überabzählbar unendlich und
verkörpert ein geometrisches Objekt, d.h. eine Menge von Punkten in der Ebene oder im Raum,
wobei die folgenden zwei Bedingungen gelten:
• Ω lässt sich als geometrisches Objekt mit endlichem Inhalt darstellen,
• Teilmengen von Ω mit gleichem Inhalt sind gleiche Wahrscheinlichkeiten zugeordnet.
Exemplarisch kann das Schießen auf eine Dartscheibe Ω betrachtet werden. Das Ereignis A
tritt ein, wenn ein bestimmtes Feld (z.B. innerer Ring) getroffen wird, d.h. A ist die Fläche
dieses Feldes als Teilmenge von Ω. Dann gilt
P (A) =
günstige Fälle
Inhalt von A
=
.
mögliche Fälle
Inhalt von Ω
Dabei gibt es Ereignisse A mit Inhalt 0 (und damit P (A) = 0), die aber keine unmöglichen
Ereignisse sind, z.B. Kurvenstücke in der Ebene oder Flächenstücke im Raum.
Beispiel. Eine Funkstation sendet zu zwei zufälligen Zeiten t1 und t2 im Zeitintervall [0, T ] je
ein punktförmiges Signal aus. Ein Empfänger kann diese beiden Signale getrennt empfangen,
wenn für ihre Zeitdifferenz |t1 − t2 | ≥ τ > 0 gilt. Wie groß ist die Wahrscheinlichkeit, dass die
beiden Signale getrennt empfangen werden können? Wir haben
Ω = {(t1 , t2 ) ∈ [0, T ] × [0, T ]}
und betrachten das Ereignis
A = {(t1 , t2 ) ∈ Ω : |t1 − t2 | ≥ τ }.
t2
T
A
τ
0
Ω\A
τ
T
Dann gilt
Fläche von A
(T − τ )2
P (A) =
=
=
Fläche von Ω
T2
(
t1
T −τ
T
)2
(
τ )2
= 1−
.
T
1.2.4 Ergänzende Beispiele zur Einführung von Wahrscheinlichkeiten
Beispiel. In einem Rechnerpool befinden sich 75 Computer an festen Standorten. Genau einmal
im Jahr wird der Pool modernisiert. Jeder Computer wird regulär nach zwei Jahren durch
16
ein moderneres Modell ersetzt. Falls jedoch ein Computer im ersten Jahr durch mindestens
fünf erforderliche Reparaturen auffällt, so wird er bereits nach einem Jahr ausgetauscht. Das
Ereignis A = „Computer fällt im ersten Jahr auf“ habe die Wahrscheinlichkeit p und Ak =
„Computer wird im k-ten Jahr ausgetauscht“ habe die Wahrscheinlichkeit pk . Wie groß ist die
Wahrscheinlichkeit pk , dass an einem fixierten Standort im k-ten Jahr ein Computeraustausch
stattfindet?
Es gilt Ak = Ak−1 ∪ (Ak−1 ∩ A) und somit ist
pk = P (Ak ) = P (Ak−1 ) + P (Ak−1 ∩ A) = 1 − P (Ak−1 ) + P (A|Ak−1 ) P (Ak−1 )
| {z }
p
= 1 − pk−1 + ppk−1 = 1 − (1 − p)pk−1 = 1 + (p − 1)pk−1 .
Aus dieser Rekursionsvorschrift ergibt sich
p1 = p = 1 + (p − 1)
(ohne Rekursionsformel)
p2 = 1 + (p − 1) + (p − 1)2
p3 = 1 + (p − 1) + (p − 1)2 + (p − 1)3
..
.
pk =
k
∑
(p − 1)i
(endliche Summe einer geometrischen Reihe)
i=0
=
1 − (p − 1)k+1
1 − (p − 1)k+1
=
.
1 − (p − 1)
2−p
Für p = 0,1 ergeben sich die folgenden Wahrscheinlichkeiten.
k
pk
1
0,1
2
0,91
3
0,181
4
0,837
5
0,247
10
0,691
20
0,584
21
0,474
∞
0,526
Beispiel. Wir betrachten die Geschlechterverteilung bei der Geburt von Zwillingen. Dabei
sind die Ereignisse K1 ∩ K2 (zwei Knaben), K1 ∩ M2 (erst Knabe, dann Mädchen), M1 ∩ M2
(zwei Mädchen) und M1 ∩ K2 (erst Mädchen, dann Knabe) möglich. Es sind die folgenden
statistischen Informationen bekannt:
• Die Wahrscheinlichkeit, dass bei einer Geburt ein Knabe zur Welt kommt, beträgt 51 %,
d.h. P (K1 ) = P (K2 ) = 0,51.
• Bei Zwillingsgeburten ist die Wahrscheinlichkeit gleichgeschlechtlicher Zwillinge 64 %,
d.h. P ((K1 ∩ K2 ) ∪ (M1 ∩ M2 )) = 0,64.
• Bei einer Zwillingsgeburt sind K1 ∩ M2 und M1 ∩ K2 gleichwahrscheinliche Ereignisse,
d.h. P (K1 ∩ M2 ) = P (M1 ∩ K2 ).
Wie groß ist die Wahrscheinlichkeit, dass der zweite geborene Zwilling ein Knabe ist, wenn der
zuerst geborene Zwilling auch ein Knabe war?
Wir haben Ω = (K1 ∩ K2 ) ∪ (M1 ∩ M2 ) ∪ (K1 ∩ M2 ) ∪ (M1 ∩ K2 ). Zusammen mit der zweiten
und dritten statistischen Information folgt daraus
P (K1 ∩ M2 ) = P (M1 ∩ K2 ) =
17
1 − 0,64
= 0,18
2
und unter Verwendung von P (K1 ) = P ((K1 ∩ M2 ) ∪ (K1 ∩ K2 )) und der ersten statistischen
Information ergibt sich
P (K1 ∩ K2 ) = P (K1 ) − P (K1 ∩ M2 ) = 0,51 − 0,18 = 0,33.
Somit ist unsere gesuchte Wahrscheinlichkeit
P (K2 |K1 ) =
P (K1 ∩ K2 )
0,33
=
= 0,647.
P (K1 )
0,51
Weiterhin gilt
P (M2 |M1 ) = 0,633,
P (M2 |K1 ) = 0,353,
18
P (K2 |M1 ) = 0,367.
1.3 Zufallsgrößen und Verteilungsfunktionen
1.3.1 Einführung
Vielfach sind die Ergebnisse von Zufallsversuchen Zahlenwerte. Häufig möchte man aber auch in
den Fällen, wo dies nicht so ist, Zahlenwerte zur Charakterisierung der Ergebnisse von Zufallssituationen verwenden. Dies geschieht mit Hilfe von Zufallsgrößen X, indem jedem Ergebnis ω
aus der Ergebnismenge Ω eine relle Zahl X(ω) als Wert der Zufallsgröße zugeordnet wird.
Definition 1.3.1. Sei (Ω, A, P ) ein Wahrscheinlichkeitsraum zu einer festen Zufallssituation.
Dann heißt eine Abbildung X : Ω 7→ R Zufallsgröße oder Zufallsvariable über (Ω, A, P ), wenn
für alle Intervalle I ⊂ R gilt:
{ω ∈ Ω : X(ω) ∈ I} ∈ A.
Für die Wahrscheinlichkeit P ({ω ∈ Ω : X(ω) ∈ I}) schreiben wir verkürzt P (X ∈ I).
Beispiel. In einer Hühnerhaltung wird das Gewicht von Eiern in Gramm ermittelt. Das Gewicht ω eines Eies ist eine zufällige positive reelle Zahl. Die Zufallsgröße X = X(ω) ordnet den
Eiern eine der drei Gewichtsklassen 1, 2 oder 3 zu:


1, ω ≤ 40
X(ω) := 2, 40 < ω ≤ 60 .


3, ω > 60
Beispiel. Beim Werfen zweier idealer Würfel erhält man die Ergebnismenge
{
}
Ω = (i, j) : i, j ∈ {1, 2, 3, 4, 5, 6} .
Die Augensumme X(ω) := i + j ist dann eine Zufallsgröße.
Beispiel. Es wird die Lebensdauer von n Glühlampen betrachtet, wobei ωi die Brenndauer
der i-ten Glühlampe in Stunden bezeichnet. Haben also
Ω = {ω = (ω1 , . . . , ωn ) : ωi ≥ 0}
als Ergebnismenge. Sowohl X(ω) := ωk (Lebensdauer der k-ten Glühlampe) als auch X(ω) :=
ω1 +...+ωn
(mittlere Lebensdauer der Glühlampen) stellen Zufallsgrößen dar.
n
1.3.2 Diskrete Zufallsgrößen
Definition 1.3.2. Eine Zufallsgröße X heißt diskret, wenn sie nur endlich oder abzählbar
unendlich viele Werte annehmen kann.
Definition 1.3.3. Sei X eine diskrete Zufallsgröße mit den Werten x1 , x2 , . . . (endlich oder
abzählbar unendlich viele) und pi := P (X = xi ). Dann heißt die Zuordnung xi 7→ pi Wahrscheinlichkeitsfunktion der Zufallsgröße X.
Eine diskrete Zufallsgröße wird vollständig durch ihre Wahrscheinlichkeitsfunktion bestimmt.
Beispiel. Beim Werfen eines idealen Würfels ist die Anzahl der möglichen Augenzahlen xi
endlich. Somit kann man die Wahrscheinlichkeitsfunktion als Tabelle darstellen.
19
i
xi
pi
1
1
2
2
3
3
4
4
5
5
6
6
1
6
1
6
1
6
1
6
1
6
1
6
Eigenschaften der Wahrscheinlichkeitsfunktion
• 0 ≤ pi ≤ 1,
∑
•
pi = 1,
i
• P (a ≤ X < b) =
∑
pi .
a≤xi <b
Definition 1.3.4. Sei X eine Zufallsgröße. Dann heißt die Funktion F (x) := P (X < x)
Verteilungsfunktion von X. Für eine diskrete Zufallsgröße X mit den Werten x1 , x2 , . . . gilt also
∑
F (x) =
pi .
xi <x
Bei diskreten Zufallsgrößen ist die Verteilungsfunktion immer eine reine Treppenfunktion.
Die Punkte xi kennzeichnen die Sprungpunkte und die Werte pi die zugehörigen Sprunghöhen.
Eigenschaften der Verteilungsfunktion
•
lim F (x) = 0,
x→−∞
• lim F (x) = 1,
x→∞
• x1 < x2 ⇒ F (x1 ) ≤ F (x2 ), d.h. F ist monoton wachsend (nicht notwendigerweise streng),
•
lim F (x) = F (x0 ), d.h. F ist linksseitig stetig.
x→x0 −0
Bekannte Zahlenreihen Wir setzen die folgenden drei Zahlenreihen als bekannt voraus und
werden sie im Weiteren benutzen:
∞
∑
xi =
i=0
∞
∑
für |x| < 1,
(1.3.1)
ixi−1 =
1
(1 − x)2
für |x| < 1,
(1.3.2)
i(i − 1)xi−2 =
2
(1 − x)3
für |x| < 1.
(1.3.3)
i=1
∞
∑
1
1−x
i=2
1.3.2.1 Erwartungswert und Varianz
Beispiel. Eine neue Maschine zur Produktion elektronischer Bauteile wird über eine Dauer
von n Tagen getestet, um herauszufinden, wie viele fehlerfreie Teile sie im Durchschnitt am
20
Tag liefert. Dabei bezeichne ni die
∑ Anzahl der Tage, an denen genau i funktionstüchtige Teile
hergestellt wurden. Es gilt also ∞
i=0 ni = n und wir erhalten als Ergebnis
∞
∞
∞
∑
∑
ni ∑
n→∞
i =
iHn (X = i) −−−−→
iP (X = i).
n
i=0
i=0
i=0
Definition 1.3.5. Ist pi = P (X = xi ) die Wahrscheinlichkeitsfunktion einer diskreten Zufallsgröße X, so wird
∑
EX :=
xi pi
i
Erwartungswert oder Mittelwert der Zufallsgröße X genannt. Der Erwartungswert ist eine endliche reelle Zahl, falls gilt
∑
|xi |pi < ∞.
i
Beispiel. Beim Würfeln mit einem idealen Würfel sei X die gewürfelte Augenzahl. Dann ist
6
∑
1
EX =
i = 3,5,
6
i=1
d.h. im Mittel wird die Augenzahl 3,5 erreicht.
Neben dem Erwartungswert für eine Zufallsgröße X kann auch der Erwartungswert von
Funktionen g(X) einer Zufallsgröße X betrachtet werden, z.B. für g(X) = X 2 oder g(X) =
sin(X).
Definition 1.3.6. Ist pi = P (X = xi ) die Wahrscheinlichkeitsfunktion einer diskreten Zufallsgröße X, so wird
∑
Eg(X) :=
g(xi )pi
i
Erwartungswert der Funktion g(X) genannt. Der Erwartungswert einer Funktion ist eine endliche reelle Zahl, falls gilt
∑
|g(xi )|pi < ∞.
i
Definition 1.3.7. Die Größe
σ 2 := D2 X := E(X − EX)2
heißt Varianz (oder Streuung oder Dispersion) der Zufallsgröße X und gibt die mittlere quadratische
Abweichung der Zufallsgröße X von ihrem Erwartungswert EX an. Die Größe σ :=
√
2
D X heißt Standardabweichung der Zufallsgröße X.
Beispiel. Wir betrachten nochmals das Würfeln mit einem idealen Würfel (siehe vorhergehendes Beispiel). Haben also EX = 3,5. Setzen wir g(X) := (X − EX)2 , so erhalten wir als
Varianz der Zufallsgröße X
D2 X = E(X − EX)2 = Eg(X) =
6
∑
1
i=1
21
6
1∑
(i − 3,5)2 = 2,92.
6
6
g(i) =
i=1
Die Standardabweichung beträgt somit σ = 1,71.
Hilfssatz 1.3.8. Für eine Zufallsgröße X gilt mit a, b ∈ R:
E(aX + b) = aEX + b.
Beweis (für diskrete Zufallsgrößen).
∑
∑
∑
∑
∑
pi = aEX + b.
E(aX + b) =
(axi + b)pi =
axi pi +
bpi = a
xi pi +b
i
i
i
| i {z }
| i{z }
EX
1
Hilfssatz 1.3.9. Für zwei Funktionen f (X) und g(X) einer Zufallsgröße X gilt:
E(f (X) + g(X)) = Ef (X) + Eg(X).
Beweis (für diskrete Zufallsgrößen).
∑
∑
∑
E(f (X) + g(X)) =
(f (xi ) + g(xi ))pi =
f (xi )pi +
g(xi )pi = Ef (X) + Eg(X).
i
i
i
Hilfssatz 1.3.10. Für eine Zufallsgröße X gilt mit a, b ∈ R:
D2 (aX + b) = a2 D2 X.
Beweis.
D2 (aX + b) = E(aX + b − E(aX + b))2 = E(aX − aEX)2 = a2 E(X − EX)2 = a2 D2 X.
| {z }
aEX+b
Satz 1.3.11. Für eine Zufallsgröße X gilt:
D2 X = EX 2 − (EX)2 .
Beweis.
D2 X = E(X − EX)2 = E(X 2 − 2XEX + (EX)2 )
= EX 2 − E(2XEX) +(EX)2 = EX 2 − (EX)2 .
| {z }
2(EX)2
Definition 1.3.12. Die Größen
mk = EX k
für k = 1, 2, . . . heißen k-te Momente der Zufallsgröße X und die Größen
µk = E(X − EX)k
22
für k = 1, 2, . . . heißen k-te zentrale Momente der Zufallsgröße X.
Offensichtlich ist m1 = EX und µ2 = E(X − EX)2 = D2 X. Weiterhin gilt µ1 = E(X −
EX) = EX − EX = 0 und nach Satz 1.3.11 ist µ2 = m2 − m21 . Häufig wird für den Erwartungswert m1 = EX ebenfalls das Symbol µ verwendet.
Definition 1.3.13. Eine Folge von Zufallsgrößen X1 , X2 , . . . , Xn heißt vollständig unabhängig,
wenn sich der zufällige Charakter aller beteiligten Zufallsgrößen nicht beeinflusst.
Hilfssatz 1.3.14. Seien X1 , . . . , Xn n Zufallsgrößen mit endlichen Erwartungswerten EXi und
endlichen Streuungen D2 Xi . Dann gilt für beliebige reelle Zahlen ai :
E(a1 X1 + · · · + an Xn ) = a1 EX1 + · · · + an EXn .
Falls die Zufallsgrößen X1 , . . . , Xn vollständig unabhängig sind, gilt außerdem:
D2 (a1 X1 + · · · + an Xn ) = a21 D2 X1 + · · · + a2n D2 Xn .
Satz 1.3.15 (Tschebyscheff’sche Ungleichung). Für alle ε > 0 gilt:
P (|X − EX| > ε) <
Setzt man k :=
√ ε
D2 X
D2 X
.
ε2
= σε , so erhält man:
P (|X − EX| > kσ) <
1
.
k2
Beweis (für diskrete Zufallsgrößen). Sei M := {i : |xi − EX| > ε}. Dann gilt
∑
∑
∑
D2 X =
(xi − EX)2 pi ≥
(xi − EX)2 pi > ε2
pi = ε2 P (|X − EX| > ε)
i
i∈M
i∈M
und somit ist
P (|X − EX| > ε) <
D2 X
.
ε2
Nachweis der schwachen Konvergenz der relativen Häufigkeit Wir werden nun die Tschebyscheff’sche Ungleichung zum Nachweis der schwachen Konvergenz (Konvergenz im Sinne
der Wahrscheinlichkeit) der relativen Häufigkeit eines Ereignisses gegen die Wahrscheinlichkeit
dieses Ereignisses nutzen.
Dazu realisieren wir n unabhängige Versuche zu einer Zufallssituation mit dem Wahrscheinlichkeitsraum (Ω, A, P ). Hn (A) sei die relative Häufigkeit des Eintretens eines Ereignisses
A ∈ A. Zu zeigen ist nun, dass Hn (A) in einem gewissen Sinn gegen die Wahrscheinlichkeit
p := P (A) strebt. Wir setzen
{
1, wenn A im i-ten Versuch eintritt
Xi =
0, wenn A im i-ten Versuch nicht eintritt
23
und erhalten somit eine Zufallsgröße
X̄n := Hn (A) =
X1 + . . . + Xn
.
n
Aus P (Xi = 1) = p und P (Xi = 0) = 1 − p folgt
EXi = 1p + 0(1 − p) = p,
EXi2 = 12 p + 02 (1 − p) = p,
D2 Xi = EXi2 − (EXi )2 = p − p2 = p(1 − p)
und nach Hilfssatz 1.3.14 gilt
EX̄n =
1
1
1
EX1 + · · · + EXn = n · p = p = P (A)
n
n
n
und ebenfalls nach Hilfssatz 1.3.14 ist
D2 X̄n =
1 2
1
1
p(1 − p)
D X1 + · · · + 2 D2 Xn = n · 2 p(1 − p) =
.
2
n
n
n
n
Die Tschebyscheff’sche Ungleichung liefert somit
P (|Hn (A) − P (A)| > ε) = P (|X̄n − EX̄n | > ε) <
D2 X̄n
p(1 − p)
=
2
ε
nε2
und daraus erhalten wir
lim P (|Hn (A) − P (A)| > ε) ≤ lim
n→∞
n→∞
p(1 − p)
= 0,
nε2
d.h. Hn (A) strebt für n → ∞ gegen P (A) (Konvergenz im Sinne der Wahrscheinlichkeit):
stoch
Hn (A) −−−−→ P (A).
n→∞
1.3.2.2 Geometrische Verteilung
Als erste diskrete Wahrscheinlichkeitsverteilung wollen wir die recht einfache geometrische Verteilung und ihre Kenngrößen betrachten und an ihr die Verwendung der obigen Begriffe demonstrieren.
Als Standardbeispiel für die geometrische Verteilung dient ein Automat, der sofort anhält,
wenn er ein fehlerhaftes Teil produziert hat, wobei die Qualität der einzelnen Teile von den
anderen Teilen unabhängig ist. Wir verwenden die folgenden Bezeichnungen:
Wahrscheinlichkeit p – Wahrscheinlichkeit, dass ein Teil fehlerhaft ist;
Zufallsgröße X – Anzahl der produzierten fehlerfreien Teile;
Ereignis Ai – i-tes produziertes Teil ist defekt.
24
Also ist P (Ai ) = p und P (Ai ) = 1 − p. Somit ergibt sich
P (X = 0) = P (A1 ) = p,
P (X = 1) = P (A1 ∩ A2 ) = (1 − p)p,
P (X = 2) = P (A1 ∩ A2 ∩ A3 ) = (1 − p)2 p,
P (X = 3) = P (A1 ∩ A2 ∩ A3 ∩ A4 ) = (1 − p)3 p,
..
.
und allgemein erhalten wir als Wahrscheinlichkeitsfunktion
P (X = i) = p(1 − p)i
(i = 0, 1, 2, . . .).
Definition 1.3.16. Ein diskrete Zufallsgröße X mit der obigen Wahrscheinlichkeitsfunktion
heißt geometrisch verteilt mit dem Parameter p.
Wie bereits am Anfang des Abschnitts über diskrete Zufallsgrößen∑erwähnt, muss für diskrete
Zufallsgrößen zum einen 0 ≤ P (X = xi ) ≤ 1 und zum anderen i P (X = xi ) = 1 gelten.
Ersteres ist offensichtlich bei der geometrischen Verteilung erfüllt:
0 ≤ p(1 − p)i ≤ 1.
Und auch die zweite Eigenschaft gilt:
∞
∑
p(1 − p) = p ·
i
i=0
∞
∑
(1 − p)i = p ·
|i=0 {z
}
p
1
= = 1.
1 − (1 − p)
p
geometrische
Reihe
P (X = x)
0
1
2
3
4
5
6
7
x
Beispiel. Für das Zahlenbeispiel p = 0,01 ist die Wahrscheinlichkeit dafür gesucht, dass wenigstens 50 fehlerfreie Teile produziert werden. Wir erhalten
P (X ≥ 50) =
∞
∑
i=50
p(1 − p) = p(1 − p)
i
50
∞
∑
(1 − p)
i−50
= p(1 − p)
i=50
1
= p(1 − p)50
= (1 − p)50 = 0,9950 = 0,605.
1 − (1 − p)
25
50
∞
∑
j=0
(1 − p)j
Erwartungswert Wir berechnen nun den Erwartungswert einer geometrisch verteilten Zufallsgröße:
EX =
∞
∑
iP (X = i) =
i=0
∞
∑
ip(1 − p)i
i=0

= p(1 − p) 0(1 − p)−1 +
| {z }
i=0
= p(1 − p)
=
1−p
.
p
1
(1 − (1 − p))2
∞
∑

i(1 − p)i−1 
i=1
(nach Formel (1.3.2))
Beispiel. Für p = 0,01 produziert die Maschine also im Mittel
0,99
0,01
= 99 fehlerfreie Teile.
Für die Berechnung der Varianz benötigen wir neben EX auch noch die Größe EX 2 :
2
EX =
∞
∑
∞
∞
∑
∑
2
i
i p(1 − p) =
(i − i)p(1 − p) +
ip(1 − p)i
2
i
i=0
i=0
|i=0
{z
}
EX

= p(1 − p)2 0(1 − p)−2 + 0(1 − p)−1 +
| {z } | {z }
i=0
i=1
∞
∑

i(i − 1)(1 − p)i−2  + EX
i=2
2
+ EX
(nach Formel (1.3.3))
p3
(p − 1)(p − 2)
2(1 − p)2 1 − p
=
=
+
.
p2
p
p2
= p(1 − p)2
Varianz Die Varianz einer geometrisch verteilten Zufallsgröße ist somit:
D2 X = EX 2 − (EX)2 =
(p − 1)(p − 2) (1 − p)2
1−p
−
=
.
p2
p2
p2
1.3.2.3 Binomialverteilung
Beispiel. Ein Automat erzeugt nacheinander Teile mit einer Ausschusswahrscheinlichkeit von
jeweils p = 0,01. Die Produktionsqualität ist von Teil zu Teil unabhängig. Gesucht ist die
Wahrscheinlichkeit, dass unter n = 10 kontrollierten Teilen genau ein fehlerhaftes Teil ist.
Die Zufallsgröße X sei die Anzahl der Ausschussteile unter den n kontrollierten Teilen. Sie
kann also die Werte 0, 1, 2, . . . , n annehmen. Mit Ai bezeichnen wir das Ereignis, dass das i-te
Teil fehlerhaft ist. Dann gilt:
(
)
P (X = 1) = P (A1 ∩ A2 ∩ · · · ∩ A10 ) ∪ (A1 ∩ A2 ∩ · · · ∩ A10 ) ∪ · · · ∪ (A1 ∩ A2 ∩ · · · ∩ A10 )
= 10p(1 − p)9 = 0,091.
26
Verallgemeinerung Sei (Ω, A, P ) ein Wahrscheinlichkeitsraum zu einer Zufallssituation und
A ∈ A sei ein festes Ereignis. Wiederholen wir einen dieser Situation entsprechenden Versuch
(unabhängig) n mal und bezeichnen wir mit der Zufallsgröße X die Anzahl der Versuche, bei
denen A eintritt, dann gilt mit P (A) = p:
( )
n k
P (X = k) =
p (1 − p)n−k
(k = 0, 1, . . . , n).
(1.3.4)
k
Definition 1.3.17. Eine Zufallsgröße X mit der obigen Wahrscheinlichkeitsfunktion heißt binomialverteilt mit den Parametern n (Zahl der Freiheitsgrade) und p (Fehlerrate). Ist X binomialverteilt, so schreiben wir X ∼ B(n, p).
P (X = k)
0
1
2
3
4
5
6
7
k
Beispiel. Ein idealer Würfel wird n = 20 mal geworfen. Gesucht ist die Wahrscheinlichkeit,
dass mindestens zweimal eine 6 gewürfelt wird. Die Zufallsgröße X ist die Anzahl der geworfenen
Sechsen und A sei das Ereignis, dass eine 6 gewürfelt wird. Dann ist p = P (A) = 16 und
X ∼ B(20, 16 ). Wir erhalten somit als Ergebnis
P (X ≥ 2) = 1 − P (X ≤ 1) = 1 − P (X = 0) − P (X = 1)
( ) ( )0 ( )20 ( ) ( )1 ( )19
5
20
1
5
20
1
−
= 0,8696.
=1−
6
6
1
6
6
0
Erwartungswert Der Erwartungswert für X ∼ B(n, p) beträgt:
( )
n
n
∑
∑
n k
n(n − 1)(n − 2) · · · (n − k + 1) k
k
p (1 − p)n−k =
EX =
p (1 − p)n−k
k
(k − 1)!
k=0
= np
k=1
n
∑
(n − 1)(n − 2) · · · ((n − 1) − (k − 1) + 1)
k=1
(k − 1)!
)
n (
∑
n − 1 k−1
= np
p (1 − p)n−k
k−1
k=1
n−1
∑ (n − 1)
= np
pj (1 − p)(n−1)−j
j
pk−1 (1 − p)n−k
(binomischer Satz)
j=0
= np(p + (1 − p))n−1 = np · 1n−1
= np.
27
Um die Varianz zu berechnen, berechnen wir zunächst EX 2 (analog zu EX):
( )
( )
n
∑
n k
n k
n−k
k
p (1 − p)
=
k(k − 1)
p (1 − p)n−k + EX
EX =
k
k
k=0
k=2
(
)
n
∑ n−2
= n(1 − n)p2
pk−2 (1 − p)n−k + EX
k−2
k=2
n−2
∑ (n − 2)
2
= n(n − 1)p
pj (1 − p)(n−2)−j + EX
j
2
n
∑
2
j=0
= n(n − 1)p (p + (1 − p))n−2 + np = n(n − 1)p2 + np.
2
Varianz Die Varianz für X ∼ B(n, p) beträgt:
D2 X = EX 2 − (EX)2 = n(n − 1)p2 + np − n2 p2 = np − np2
= np(1 − p).
Beispiel. Im obigen Würfelbeispiel ist EX = 20 · 16 = 3,33. Es werden also bei 20 Würfen
im Mittel 3 bis 4 Sechsen gewürfelt. Die Varianz beträgt D2 X = 20 · 61 · 56 = 25
9 = 2,78.
Nun interessiert uns noch, mit welcher Wahrscheinlichkeit die tatsächlich erreichte Anzahl von
Sechsen um mehr als 3 vom Mittelwert abweicht. Dazu nutzen wir die Tschebyscheff’sche
Ungleichung:
1 25
1
= 0,31.
P (|X − EX| > 3) < D2 X = ·
9
9 9
Somit tritt in durchschnittlich 31 % aller Fälle eine so große Abweichung vom Mittelwert auf.
Wenn wir diese Wahrscheinlichkeit exakt berechnen, so erhalten wir:
P (X = 0) + P (X = 7) + P (X = 8) + · · · + P (X = 20) = 0,063.
Es sind also in Wirklichkeit nur reichlich 6 % aller Fälle, bei denen eine Abweichung von mehr
als 3 vom Mittelwert auftritt. Die Tschebyscheff’sche Ungleichung liefert insofern eine recht
grobe Abschätzung.
Rekursionsformel Für eine binomialverteilte Zufallsgröße X ∼ B(n, p) gilt:
P (X = k + 1) =
n−k
p
·
· P (X = k).
k+1 1−p
∑
Somit ist nk=m P (X = k) von der unteren Indexgrenze beginnend leicht mit einem Taschenrechner auszuwerten.
28
1.3.2.4 Poisson-Verteilung
Als Referenzmodell für die Poisson-Verteilung dient eine Telefonzentrale: Innerhalb eines Zeitintervalls der Länge t kommen Xt Anrufe (= Ereignisse) an und es gelten die sogenannten
Poisson’schen Voraussetzungen:
• Stationarität: Die Wahrscheinlichkeit für das Eintreten einer bestimmten Anzahl von
Ereignissen im betrachteten Zeitintervall hängt nur von der Intervalllänge und nicht von
der Lage des Intervalls auf der Zeitachse ab.
• Homogenität: Die Ereignisfolge ist nachwirkungsfrei, d.h. die Anzahl von Ereignissen im
Zeitintervall [t0 , t1 ] hat keinen Einfluss auf die Anzahl von Ereignissen in einem späteren
Zeitintervall [t2 , t3 ], wobei t1 < t2 .
• Ordinarität: Die Ereignisse treten für hinreichend kleine Zeitintervalle einzeln auf, d.h. für
genügend kleine ∆t gilt entweder X∆t = 0 oder X∆t = 1. Zudem gilt P (X∆t = 1) = µ∆t
mit 0 < µ < ∞. Der Parameter µ heißt Intensität.
Unter diesen Voraussetzungen gilt:
P (Xt = k) =
(µt)k −µt
e
k!
(1.3.5)
(k = 0, 1, 2, . . .).
Diese Formel erhalten wir, indem wir die beschriebene Verteilung als Grenzfall der Binomialverteilung auffassen: Wir teilen das Zeitintervall der Länge t in n hinreichend kleine Teilintervalle mit Länge ∆t = nt und betrachten den Fall n → ∞. Für endliches n ist Xt binomialverteilt (k Teilintervalle mit einem Anruf, n − k Teilintervalle mit null Anrufen) und mit
p = P (X∆t = 1) = µ∆t erhalten wir aus Formel (1.3.4):
( )
( ) ( )k (
)
n
n
µt
µt n−k
k
n−k
P (Xt = k) =
(µ∆t) (1 − µ∆t)
=
1−
k
k
n
n
( )k (
)n−k
n!
µt
µt
=
1−
k!(n − k)! n
n
(
) (
)
k
µt n
µt −k
(µt) n(n − 1) · · · (n − k + 1)
·
1−
1−
=
k
k!
n
n
n
|
{z
}|
{z
}|
{z
}
→1
−−−−→
n→∞
(µt)k
k!
→e−µt
→1
e−µt .
Definition 1.3.18. Eine Zufallsgröße Xt mit der Wahrscheinlichkeitsfunktion (1.3.5) heißt
Poisson-verteilt und wir schreiben Xt ∼ πµt . Oft wird λ := µt gesetzt. Ist Xt Poisson-verteilt
mit dem Parameter λ, so schreiben wir Xt ∼ πλ .
Die Wahrscheinlichkeiten πλ (k) = P (Xt = k) findet man für übliche Parameterwerte λ in
Tabellen.
29
P (X = k)
0
1
2
3
4
5
6
7
k
Beispiel. Wir betrachten die Anzahl der eingehenden Anrufe in einer Telefonzentrale. Wir
rechnen in Minuten und setzen µ = 13 , d.h. mit einer Wahrscheinlichkeit von 13 kommt innerhalb einer Minute genau ein Anruf an. Gesucht ist die Wahrscheinlichkeit dafür, dass in einer
Viertelstunde wenigstens 3 und höchstens 7 Anrufe ankommen. Unsere Zufallsgröße Xt ist also
die Anzahl der innerhalb von t = 15 Minuten eingehenden Anrufe und λ = µt = 5. Da Xt ∼ π5 ,
erhalten wir:
7
7
∑
∑
(15µ)k −15µ
π5 (k) =
e
= 0,742.
P (3 ≤ Xt ≤ 7) =
k!
k=3
k=3
Rekursionsformel Für eine Poisson-verteilte Zufallsgröße Xt ∼ πλ gilt:
P (Xt = k + 1) =
λ
λk
λ
λk+1 −λ
e =
· e−λ =
P (Xt = k).
(k + 1)!
k + 1 k!
k+1
∑
Somit ist nk=m P (Xt = k) von der unteren Indexgrenze beginnend leicht mit einem Taschenrechner auszuwerten.
Erwartungswert Der Erwartungswert für Xt ∼ πλ beträgt:
∞
∞
∞
∑
∑
∑
λk−1
λj
λk −λ
−λ
−λ
k e = λe
= λe
= λe−λ eλ = λ.
EXt =
k!
(k − 1)!
j!
j=0
k=1
k=0
t
Somit gibt der Parameter µ = λt = EX
t die mittlere Ereignisanzahl pro Zeiteinheit an. Um die
Varianz zu berechnen, benötigen wir noch EXt2 :
EXt2
=
∞
∑
k
k
2 λ −λ
k=0
= λ2 e−λ
k!
e
=
∞
∑
k=0
∞
∑
λj
j=0
j!
∞
∑ λk−2
λk
k(k − 1) e−λ + EXt = λ2 e−λ
+ EXt
k!
(k − 2)!
k=2
+ EXt = λ2 E −λ eλ + EXt = λ2 + λ.
Varianz Die Varianz für Xt ∼ πλ beträgt:
D2 Xt = EXt2 − (EXt )2 = λ2 + λ − λ2 = λ.
30
1.3.2.5 Hypergeometrische Verteilung
Als Referenzmodell dient die bereits bekannte Urne mit N Kugeln, von denen M Kugeln
schwarz und N − M Kugeln weiß sind. Wir ziehen ohne Zurücklegen n Kugeln, wobei unsere
Zufallsgröße X die Anzahl der entnommenen schwarzen Kugeln ist. Dann gilt:
(M )(N −M )
P (X = m) =
m
,
(Nn−m
)
n
wobei max(0, n − (N − M )) ≤ m ≤ min(n, M ) ist.
Definition 1.3.19. Eine Zufallgröße X mit der obigen Wahrscheinlichkeitsfunktion heißt hypergeometrisch verteilt und wir schreiben X ∼ H(n, N, M ).
P (X = m)
0
1
2
3
4
5
6
7
m
Erwartungswert Der Erwartungswert für X ∼ H(n, N, M ) beträgt:
EX = n
M
.
N
Varianz Die Varianz für X ∼ H(n, N, M ) beträgt:
(
)
M N −n
M
2
D X=n
1−
.
N
N N −1
1.3.3 Stetige Zufallsgrößen
Im Abschnitt über Wahrscheinlichkeitsräume haben wir bereits die Brenndauer einer Glühlampe und die Reichweite eines Fahrzeugs bei begrenztem Treibstoffvorrat als Beispiele für stetige
Zufallsgrößen betrachtet. Da stetige Zufallsgrößen überabzählbar unendlich viele Werte besitzen und somit deren Werte ganze Intervalle der reellen Achse ausfüllen können, ist es nicht mehr
möglich, die Wahrscheinlichkeit für jeden einzelnen Wert in einer Wahrscheinlichkeitsfunktion
auszudrücken. Jedoch kann man mit Hilfe sogenannter Dichtefunktionen die Verteilung der
Wahrscheinlichkeitsmasse auf der reellen Achse angeben und so die Wahrscheinlichkeit dafür
charakterisieren, dass der Wert der Zufallsgröße in einem gegebenen Intervall liegt.
31
Definition 1.3.20. Eine Zufallsgröße X heißt stetig, wenn es eine integrierbare reelle Funktion
f gibt, so dass für beliebige reelle Zahlen a ≤ b gilt:
∫b
P (a ≤ X ≤ b) =
f (x) dx.
a
Die Funktion f heißt Dichtefunktion der Zufallsgröße X.
Eigenschaften von Dichtefunktionen
• f (x) ≥ 0 für alle x ∈ R,
•
∫∞
f (x) dx = 1.
−∞
Das Integral ist dabei im Sinne von Riemann oder Lebesgue zu verstehen. Als Dichtefunktionen f treten vorzugsweise stetige und stückweise stetige Funktionen auf, die auch schwache
Polstellen besitzen dürfen. Die Fläche unter dem Graphen von f bleibt mit dem Wert 1 jedoch
stets endlich. Wegen
∫a
P (X = a) = P (a ≤ X ≤ a) =
f (x) dx = 0
a
ist die Wahrscheinlichkeit, dass X genau einen festen Wert annimmt, immer gleich Null.
Definition 1.3.21. Die durch
∫x
F (x) = P (X < x) =
f (t) dt
−∞
definierte reelle Funktion F heißt Verteilungsfunktion der stetigen Zufallsgröße X.
Eigenschaften der Verteilungsfunktion
•
lim F (x) = 0.
x→−∞
• lim F (x) = 1.
x→∞
• x1 < x2 ⇒ F (x1 ) ≤ F (x2 ), d.h. F ist monoton wachsend (nicht notwendigerweise streng).
• P (a ≤ X ≤ b) = F (b) − F (a).
• F ist stetig in allen Punkten x ∈ R.
• Falls die Dichtefunktion f in x0 stetig ist, so ist F in x0 differenzierbar und es gilt
F ′ (x0 ) = f (x0 ).
32
1.3.3.1 Erwartungswert und Varianz
Definition 1.3.22. Der Erwartungswert einer stetigen Zufallsgröße X ist gegeben durch
∫∞
EX :=
xf (x) dx.
−∞
EX ist eine endliche Zahl, wenn gilt
∫∞
|x|f (x) dx < ∞.
−∞
Definition 1.3.23. Sei X eine stetige Zufallsgröße. Der Erwartungswert einer Funktion g(X)
ist gegeben durch
∫∞
Eg(X) :=
g(x)f (x) dx.
−∞
Eg(X) ist eine endliche Zahl, wenn gilt
∫∞
|g(x)|f (x) dx < ∞.
−∞
Definition 1.3.24. Die Varianz (oder Streuung) einer stetigen Zufallsgröße X ist wie im
diskreten Fall definiert durch
σ 2 := D2 X := E(X − EX)2 .
Die folgenden Sätze aus Abschnitt 1.3.2.1 gelten auch für stetige Zufallsgrößen:
• Hilfssatz 1.3.8: E(aX + b) = aEX + b.
• Hilfssatz 1.3.10: D2 (aX + b) = a2 D2 X.
• Satz 1.3.11: D2 X = EX 2 − (EX)2 .
• Satz 1.3.15 (Tschebyscheff’sche Ungleichung): Für ε > 0 gilt:
P (|X − EX| > ε) <
D2 X
.
ε2
Beweis. Sei M := {x : |x − EX| > ε}. Dann gilt:
∫∞
∫
(x − EX) f (x) dx ≥
2
(x − EX)2 f (x) dx
2
D X=
−∞
M
∫
f (x) dx = ε2 P (M ) = ε2 P (|x − EX| > ε).
> ε2
M
33
1.3.3.2 Gleichverteilung
Als erste stetige Wahrscheinlichkeitsverteilung betrachten wir die recht einfache Gleichverteilung. Wir nennen eine Zufallsgröße X gleichverteilt auf dem Intervall [a, b], wenn X nur Werte
aus dem Intervall annehmen kann und diese gleichwahrscheinlich über das Intervall verteilt
sind. Für die Dichtefunktion ergibt sich also:
{
c, x ∈ [a, b]
f (x) =
,
0, x ̸∈ [a, b]
wobei c = const eine Konstante ist. Wegen
∫b
c(b − a) =
∫b
c dx =
a
erhalten wir c =
∫∞
f (x) dx =
f (x) dx = 1
−∞
a
1
b−a .
Definition 1.3.25. Ein stetige Zufallsgröße X mit der Dichtefunktion
{
1
, x ∈ [a, b]
f (x) = b−a
0,
x ̸∈ [a, b]
heißt gleichverteilt mit den beiden Parametern a und b.
f (x)
a
b
x
Die Verteilungsfunktion F nimmt offensichtlich für x < a den Wert 0 und für x > b den Wert 1
an. Für a ≤ x ≤ b ergibt sich:
∫x
F (x) =
∫x
f (t) dt =
−∞
a
t x x − a
1
=
dt =
,
b−a
b − a a
b−a
34


0,
also ist
F (x) =
x−a
,
 b−a

1,
x<a
a≤x≤b.
x>b
Erwartungswert Für den Erwartungswert einer gleichverteilten stetigen Zufallsgröße X erhalten wir:
b
∫∞
∫b
x
x2 b 2 − a2
a+b
EX =
xf (x) dx =
dx =
=
=
.
b−a
2(b − a) a 2(b − a)
2
−∞
a
Zur Berechnung der Varianz benötigen wir noch EX 2 .
∫b
2
EX =
a
b
x2
x3 b3 − a3
a2 + ab + b2
dx =
=
=
.
b−a
3(b − a) a 3(b − a)
3
Varianz Für die Varianz einer gleichverteilten stetigen Zufallsgröße X erhalten wir also:
D2 X = EX 2 − (EX)2 =
a2 + ab + b2 a2 + 2ab + b2
a2 − 2ab + b2
(a − b)2
−
=
=
.
3
4
12
12
1.3.3.3 Exponentialverteilung
Definition 1.3.26. Besitzt eine stetige Zufallsgröße X die Dichtefunktion
{
0,
x≤0
f (x) =
,
−λx
λe
, x>0
so nennen wir X exponentialverteilt mit dem Parameter λ > 0 und schreiben X ∼ Ex(λ).
f (x)
0
x
Aus der Dichtefunktion f erhält man die Verteilungsfunktion
{
0,
x≤0
F (x) =
.
−λx
1−e
, x>0
35
Zusammenhang zwischen Exponential- und Poisson-Verteilung Im Unterabschnitt über
die Poisson-Verteilung haben wir als Modell eine Telefonzentrale betrachtet, wobei die Zufallsgröße Xt die Anzahl der Anrufe in einem Zeitintervall der Länge t beschrieb. Xt war Poissonverteilt mit dem Parameter µ. Dabei gab µ die durchschnittliche Anrufanzahl pro Zeiteinheit
an. Dieses Modell können wir auch nutzen, um die Exponentialverteilung zu veranschaulichen.
Betrachten wir als Zufallsgröße T die Länge des Zeitintervalls zwischen zwei eingehenden Anrufen, so ist T exponentialverteilt mit demselben Parameter µ wie bei der Poisson-Verteilung.
Beispiel. In einer Telefonzentrale kommen im Mittel 20 Anrufe pro Stunde an. Gesucht ist
die Wahrscheinlichkeit, dass zwischen zwei Anrufen 3 bis 6 Minuten vergehen. Rechnen wir in
1
Minuten, so ist µ = 20
60 = 3 . Wir erhalten dann:
(
) (
)
P (3 ≤ T ≤ 6) = F (6) − F (3) = 1 − e−6µ − 1 − e−3µ = e−1 − e−2 = 0,2325.
Exponentialverteilung als Lebensdauerverteilung Wartezeiten, Reparaturzeiten und die Lebensdauer von Bauelementen können als exponentialverteilt angenommen werden. Wie die
folgende Überlegung zeigt, muss dabei jedoch beachtet werden, dass keine Alterungseffekte
modelliert werden können: Für X ∼ Ex(λ) gilt
F (x0 + x) − F (x0 )
P (x0 ≤ X ≤ x0 + x)
=
P (X ≥ x0 )
1 − F (x0 )
(
)
(
)
1 − e−λ(x0 +x) − 1 − e−λx0
e−λx0 − e−λ(x0 +x)
=
=
1 − (1 − e−λx0 )
e−λx0
P (X ≤ x0 + x|X ≥ x0 ) =
= 1 − e−λx = P (X ≤ x),
d.h. wenn wir als Zufallsgröße X die Lebensdauer eines Bauelements betrachten, so ist die
Wahrscheinlichkeit, dass das Bauelement innerhalb einer Zeitdauer x eine Störung aufweist,
unabhängig davon, ob es bereits über eine Zeitdauer x0 in Betrieb war oder ob es neu ist.
Erwartungswert Der Erwartungswert für X ∼ Ex(λ) beträgt:


∫∞
∫∞
∫∞
(
)
1
1
1
∞
te−t dt =  t −e−t 0 + e−t dt = .
EX = xλe−λx dx =
λ
λ
λ
0
0
In ähnlicher Weise berechnet man EX 2 =
0
2
.
λ2
Varianz Die Varianz für X ∼ Ex(λ) beträgt:
D2 X = EX 2 − (EX)2 =
1
1
2
− 2 = 2.
2
λ
λ
λ
Beispiel. Als Zufallsgröße X betrachten wir die Zeitdauer für eine PKW-Inspektion in einer
Werkstatt. Im Mittel dauert eine Inspektion 2 Stunden. Wie groß ist die Wahrscheinlichkeit,
dass eine Inspektion länger als 3 Stunden dauert? Als Einheit für unsere Berechnung wählen
wir Stunden und es sei X ∼ Ex(λ). Somit erhalten wir aus EX = 2 den Parameter λ = 12 . Es
36
ergibt sich
(
)
3
P (X > 3) = P (X ≥ 3) = P (3 ≤ X < ∞) = F (∞) − F (3) = 1 − 1 − e−3λ = e− 2 = 0,223,
d.h. in durchschnittlich 22,3 % aller Fälle dauert die Inspektion länger als 3 Stunden.
1.3.3.4 Normalverteilung
Die Normalverteilung (oder auch Gauß’sche Verteilung) ist die wichtigste stetige Verteilung,
da sie in der Praxis eine Vielzahl von Anwendungen hat.
Definition 1.3.27. Besitzt eine stetige Zufallsgröße X die Dichtefunktion
−(x−µ)2
1
f (x) = √
e 2σ2 ,
2πσ
so nennen wir X normalverteilt mit den Parametern µ und σ 2 (σ > 0) und schreiben X ∼
N(µ, σ 2 ).
Interpretation der Parameter Die Dichtefunktion der Normalverteilung wird aufgrund ihrer
Form als Glockenkurve bezeichnet. Glockenkurven sind symmetrische, eingipfelige Kurven mit
Wendestellen bei x = µ ± σ und einem auf der Symmetrieachse liegenden Maximum (Top der
1
Glocke) von √2πσ
. Wir nennen µ ∈ R den Lageparameter, da µ die Lage der Symmetrieachse
2
angibt, und σ > 0 den Formparameter, da σ 2 den Breitenverlauf der Glockenkurve festlegt.
Bei großem σ ist die Glockenkurve breit gezogen, bei kleinem σ ist sie nadelförmig.
f (x)
µ−σ
µ+σ
µ
x
Verteilungsfunktion Die Verteilungsfunktion F einer normalverteilten Zufallsgröße ist gegeben durch
∫x
∫x
−(t−µ)2
1
√
F (x) =
f (t) dt =
e 2σ2 dt.
2πσ
−∞
−∞
F ist nicht durch einen geschlossenen analytischen Ausdruck darstellbar. Die Funktionswerte
müssen mittels numerischer Integration oder durch andere Techniken näherungsweise bestimmt
werden. Weiter unten werden wir sehen, dass es genügt, die Werte der Verteilungsfunktion für
µ = 0 und σ = 1 zu kennen. Diese sind in Tabellen erfasst.
37
Erwartungswert und Varianz Für X ∼ N(µ, σ 2 ) ist der Erwartungswert EX = µ und die
Varianz beträgt D2 X = σ 2 .
Standardisierung einer Zufallsgröße Die lineare Transformation
X − EX
Y := √
D2 X
einer Zufallsgröße X heißt Standardisierung von X. Aufgrund der Linearität dieser Transformation besitzt Y die gleiche Verteilungsart wie X. Für den Erwartungswert von Y erhalten
wir
X − EX
1
EY = E √
= 2 (EX − EX) = 0
2
D X
D X
und die Varianz beträgt
D2 Y = EY 2 = E
(X − EX)2
1
1
= 2 E(X − EX)2 = 2 D2 X = 1.
2
D X
D X
D X
Standardisierung einer normalverteilten Zufallsgröße Wenden wir das beschriebene Standardisierungsverfahren auf eine Zufallsgröße X ∼ N(µ, σ 2 ) an, so erhalten wir die entsprechende
standardisiert normalverteilte Zufallsgröße Y ∼ N(0, 1) mit Y = X−µ
σ . Als Dichtefunktion der
standardisierten Normalverteilung ergibt sich
x2
1
φ(x) = √ e− 2
2π
und somit ist die Verteilungsfunktion
∫x
Φ(x) =
−∞
t2
1
√ e− 2 dt.
2π
Für x ≥ 0 sind die Funktionswerte von Φ tabelliert. Für x < 0 nutzt man den aus der Symmetrie
der Glockenkurve resultierenden Zusammenhang Φ(−x) = 1 − Φ(x).
Berechnung von Wahrscheinlichkeiten In der Praxis müssen oft Wahrscheinlichkeiten des
Typs P (a ≤ X ≤ b) mit einer Zufallsgröße X ∼ N(µ, σ 2 ) berechnet werden. Durch Ausnutzung
der Standardisierung einer Zufallsgröße führt man solche Berechnungen auf die Berechnung
einer Differenz zweier Werte der Verteilungsfunktion Φ der standardisierten Normalverteilung
zurück, da diese Werte in Tabellen erfasst sind:
(
)
(
)
a−µ
X −µ
b−µ
a−µ
b−µ
P (a ≤ X ≤ b) = P
≤
≤
=P
≤Y ≤
σ
σ
σ
σ
σ
(
)
(
)
b−µ
a−µ
=Φ
−Φ
.
σ
σ
Anwendung normalverteilter Zufallsgrößen Stetige Fehlergrößen (Messfehler usw.) können
im Allgemeinen in guter Näherung als normalverteilt angenommen werden. Die Normalverteilung ist insbesondere dann für die Beschreibung von stochastischen Modellen geeignet, wenn
38
sich die betrachtete Zufallsgröße als Summe einer großen Anzahl von unabhängigen Einflüssen
ergibt (z.B. als Summe zahlreicher kleiner Fehler oder Störungen).
Satz 1.3.28 (Additionssatz). Seien Xi ∼ N(µi , σi2 ) für i = 1, 2, . . . , n vollständig unabhängige
normalverteilte Zufallsgrößen. Dann gilt
)
( n
n
n
∑
∑
∑
2
Z :=
Xi ∼ N
µi ,
σi ,
i=1
i=1
i=1
d.h. die Summe Z ist wieder eine normalverteilte Zufallsgröße.
Beispiel. Der Kern eines Transformators bestehe aus 25 Blechen und 24 zwischen diesen Blechen liegenden Isolierschichten. Für die Dicken (in Millimeter) Xi der Bleche und Yj der Isolierschichten gelte Xi ∼ N(0,8; 0,042 ) und Yj ∼ N(0,2; 0,032 ). Uns interessieren die folgenden
beiden Fragen:
1. Wie groß ist die Wahrscheinlichkeit, dass zwei Bleche und eine Isolierschicht zusammen
dicker als 1,85 mm sind?
2. Die Spulenöffnung sei 25,3 mm breit. Wie groß ist die Wahrscheinlichkeit, dass der Kern
zu dick ist?
Wir wissen aus dem vorhergehenden Satz, dass Z := X1 + Y1 + X2 ∼ N(1,8; 0,0041) ist. Somit
erhalten wir als Antwort auf Frage 1:
)
(
Z − 1,8
1,85 − 1,8
= 1 − Φ(0,7809) = 0,2174.
P (Z > 1,85) = P √
≥ √
0,0041
0,0041
Mit Z :=
25
∑
i=1
Xi +
24
∑
Yj ∼ N(24,8; 0,0616) ergibt sich für Frage 2:
j=1
(
P (Z > 25,3) = P
Z − 24,8
25,3 − 24,8
√
≥ √
0,0616
0,0616
)
= 1 − Φ(2,015) = 0,022.
1.3.3.5 Schiefe und Exzess
Wir betrachten neben der Varianz σ 2 = D2 X, d.h. neben dem zweiten zentralen Moment µ2
(siehe Definition 1.3.12), nun auch die dritten und vierten zentralen Momente µ3 = E(X −EX)3
und µ4 = E(X − EX)4 einer Zufallsgröße X.
Definition 1.3.29. Sei X eine Zufallsgröße. Dann heißen
γ1 :=
µ3
µ3
= (√ )3
3
σ
µ2
und
γ2 :=
µ4
−3
σ4
Schiefe von X und Exzess von X.
Die Schiefe γ1 ist ein Maß für die Asymmetrie der Verteilung, also für die Abweichung des
Verhaltens der Zufallsgröße X von dem einer symmetrischen Verteilung. Da bei einer symmetrischen stetigen Zufallsgröße X für alle x ∈ R f (µ − x) = f (µ + x) gilt, wobei x = µ = EX
39
die Symmetrieachse der (symmetrischen) Dichtefunktion f ist, erhalten wir
∫∞
µ3 = E(X − EX) =
∫µ
(x − µ) f (x) dx =
3
3
−∞
−∞
∫∞
=−
∫∞
(x − µ) f (x) dx + (x − µ)3 f (x) dx
3
µ
∫∞
x3 f (µ − x) dx +
0
x3 f (µ + x) dx = 0
0
und somit ist die Schiefe γ1 einer symmetrischen Zufallsgröße gleich Null.
Der Exzess γ2 ist ein Maß für die Abweichung der Zufallsgröße X von der Normalverteilung.
Den Quotienten σµ44 nennt man Wölbung. Der Exzess ist also die um 3 verminderte Wölbung.
Wie wir weiter unten sehen werden, gilt für eine normalverteilte Zufallsgröße µ4 = 3σ 4 . Somit
ist der Exzess einer normalverteilten Zufallsgröße gleich Null.
Satz 1.3.30. Schiefe und Exzess einer Zufallsgröße X bleiben bei Standardisierung unverändert,
d.h. mit Y := X−µ
gilt γ1 (X) = γ1 (Y ) und γ2 (X) = γ2 (Y ).
σ
Beweis. Da Y eine standardisierte Zufallsgröße ist, gilt EY = 0 und D2 Y = 1. Somit erhalten
wir
(
)
X − µ 3 E(X − EX)3
E(Y − EY )3
µ3
3
γ1 (Y ) = (√
=
= 3 = γ1 (X).
)3 = EY = E
3
σ
σ
σ
D2 Y
Der Beweis für γ2 erfolgt analog.
Satz 1.3.31. Existieren für eine Zufallsgröße X die ersten vier zentralen Momente, so gilt
γ2 ≥ γ12 − 2.
Satz 1.3.32. Sei X ∼ N(µ, σ 2 ) eine normalverteilte Zufallsgröße. Dann gilt für k = 1, 2, . . .
µ2k−1 = 0,
µ2k =
(2k)! 2k
σ
2k k!
und γ1 = γ2 = 0.
1.3.3.6 Die charakteristische Funktion
Zur Charakterisierung der Verteilung einer Zufallsgröße X kann neben der Verteilungsfunktion F (x) auch die (komplexwertige) charakteristische Funktion φX (t) verwendet werden. Wir
betrachten dies für stetige Zufallsgrößen X.
Definition 1.3.33. Sei X eine stetige Zufallsgröße. Dann heißt
φX (t) := EeitX
(t ∈ R)
∫∞
=
eitx f (x)dx
−∞
charakteristische Funktion von X. Dabei bezeichnet f (x) die Dichtefunktion von X.
40
Bemerkung.
a) Aus der trigonometrischen Darstellung einer komplexen Zahl folgt
φX (t) = E(cos tX + i sin tX) = E
| cos
{z tX} +i E
| sin
{z tX}
Realteil
=⇒ |φX (t)| ≤
∫∞
−∞
=
|eitx |
| {z }
√
∫∞
f (x)dx =
Imaginärteil
∀t ∈ R
f (x)dx = 1
−∞
cos2 φ+sin2 φ=1
b) φX (t) = φX (−t) = E cos tX + iE sin tX
c) Sei Y = aX + b. Dann ist φY (t) = Eeit(aX+b) = eitb EeitaX = eitb φX (at)
µit
Speziell bei der Standardisierung: b = − σµ , a = σ1 : ⇒ φY (t) = e− σ φX ( σt )
d) φX (t) ist eine gleichmäßig stetige Funktion, d. h. es gilt
|φX (t) − φX (t′ )| < ε, sobald |t − t′ | < δ(ε)
Beispiel. Sei X ∼ N(0, 1). Unter Benutzung des komplexen Integrals
gilt
∫∞
φX (t) =
−∞
x2
1
1
eitx √ e− 2 dx = √
2π
2π
1
=√
2π
∫∞
e−
(x−it)2
2
∫∞
eitx−
x2
2
∫∞
−∞ e
−
(x−it)2
2
dx =
dx
−∞
t2
e− 2 dx
−∞
2
=e
− t2
Daraus berechnet man die charakteristische Funktion für X̃ ∼ N(µ, σ), X̃ = σX + µ:
φX̃ (t) = eitµ φX (σt)
= eitµ e−
= eitµ−
σ 2 t2
2
σ 2 t2
2
(reellwertig für µ)
Die charakteristische Funktion wird zudem zur Berechnung von Momenten genutzt:
∫∞
eitx f (x)dx
φX (t) =
φ′X (t) =
−∞
∫∞
ixeitx f (x)dx
−∞
∫∞
φ′X (0) = i
xf (x)dx = iEX
−∞
41
⇒ m1 = EX =
φ′X (0)
i
√
2π
Analog folgt:
[
(k)
φ (0)
mk = EX k = X k
i
]
(k = 1, 2, . . .)
Bemerkung.
)2
φ′′X (0) ( ′
− φX (0)
2
i
]
D2 X = m2 − m21 =
[
D2 X = −φ′′X (0) + (φ′X (0))2
Beispiel. Sei X ∼ N(µ, σ) eine normalverteilte Zufallsgröße. Die zugehörige charakteristische
Funktion ist
φX (t) = eitµ−
σ 2 t2
2
und die erste Ableitung ist
φ′X (t) = (iµ − σ 2 t)eitµ−
σ 2 t2
2
.
Mit obiger Formel berechnet sich der Erwartungswert durch
EX =
φ′X (0)
iµ
=
= µ
i
i
sowieso analog die Varianz als D2 X = σ 2 .
Die charakteristische Funktion ist auch interessant für Summen von Zufallsgrößen:
Satz 1.3.34. Seien X und Y stochastisch unabhängige Zufallsgrößen mit den charakteristischen
Funktionen φX (t) und φY (t). Dann gilt für die charakteristische Funktion der Zufallsgröße
Z =X +Y
φZ (t) = φX (t)φY (t).
2 ) und Y ∼ N(µ , σ 2 ) normalverteilte Zufallsgrößen mit den
Beispiel. Seien X ∼ N(µX , σX
Y
Y
charakteristischen Funktionen φX (t) = eiµX t−
2 t2
σX
2
und φY (t) = eiµY t−
φZ (t) = ei(µX +µY )t−
2 +σ 2 )t2
(σX
Y
2
2
⇒ Z ∼ N(µX + µY , σX
+ σY2 ).
Satz 1.3.35. Existieren alle Momente, so gilt
φX (t) = 1 +
∞
∑
mk
k=1
k!
(it)k =
42
∞
(k)
∑
φ (0)
X
k=0
k!
tk ,
2 t2
σY
2
. Dann folgt
falls die charakteristische Funktion in t0 = 0 in eine Potenzreihe entwickelt werden kann.
Bemerkung. Die charakteristische Funktion ist die Fourriertransformierte der Dichtefunktion.
Die Rücktransformation ist möglich:
fX (x) =
1
2π
∫∞
e−itx φX (t)dt.
−∞
1.4 Das Gesetz der großen Zahlen und Grenzverteilungssätze
In vielen Anwendungen, vor allem in der mathematischen Statistik, treten Folgen von Zufallsgrößen X1 , X2 , . . . , Xn und deren Linearkombinationen
Yn := a1 X1 + a2 X2 + · · · + an Xn
auf. Dabei gilt nach Hilfssatz 1.3.14
EYn =
n
∑
ai EXi
i=1
und, falls X1 , . . . , Xn vollständig unabhängig sind,
D2 Yn =
n
∑
a2i D2 Xi .
i=1
Definition 1.4.1. Die Zufallsgrößen X1 , . . . , Xn heißen unabhängig und identisch verteilt oder
vom Typ i.i.d. (von „independent and identically distributed“), wenn sie vollständig unabhängig
sind, identische Verteilungen aufweisen und die Erwartungswerte und Streuungen existieren. Es
gilt also
EX1 = · · · = EXn =: µ ∈ R,
D2 X1 = · · · = D2 Xn =: σ 2 < ∞.
Sind X1 , . . . , Xn Zufallsgrößen vom Typ i.i.d. und ist
X̄n =
X1 + · · · + Xn
n
ihr arithmetisches Mittel, so gilt
EX̄n =
n
∑
1
µ = µ,
n
D2 X̄n =
n
∑
1 2 σ2
σ =
.
n2
n
(1.4.1)
i=1
i=1
1.4.1 Das Gesetz der großen Zahlen
Satz 1.4.2 (schwaches Gesetz der großen Zahlen). Sind X1 , . . . , Xn Zufallsgrößen vom Typ
i.i.d. und ist µ = EX̄n = EXi deren einheitlicher Erwartungswert, so gilt für alle ε > 0
(
)
lim P |X̄n − µ| ≤ ε = 1,
n→∞
43
d.h. das arithmetische Mittel X̄n konvergiert für wachsendes n im Sinne der Wahrscheinlichkeit
gegen den einheitlichen Erwartungswert der Zufallsgrößen X1 , . . . , Xn .
Beweis. Mit σ 2 = D2 X1 = · · · = D2 Xn erhalten wir aus der Tschebyscheff’schen Ungleichung und den Formeln (1.4.1):
(
)
(
)
D2 X̄n
σ2
P |X̄n − µ| ≤ ε = 1 − P |X̄n − EX̄n | > ε > 1 −
=
1
−
.
ε2
nε2
Für n gegen unendlich ergibt sich also:
)
(
σ2
1 − 2 = 1.
n→∞
nε
(
)
1 ≥ lim P |X̄n − µ| ≤ ε ≥ lim
n→∞
Am Ende von Abschnitt 1.3.2.1 haben wir die Aussage des obigen Satzes bereits verwendet,
um zu zeigen, dass die relative Häufigkeit Hn (A) = X̄n eines Ereignisses A für wachsendes n
(Versuchsanzahl) gegen die Wahrscheinlichkeit p = P (A) strebt. Dabei waren X1 , . . . , Xn mit
{
1, wenn A im i-ten Versuch eintritt
Xi =
0, wenn A im i-ten Versuch nicht eintritt
Zufallsgrößen vom Typ i.i.d. und es galt µ = EX̄n = p und σ 2 = D2 X̄n =
obigem Satz
lim P (|Hn (A) − p| ≤ ε) = 1.
p(1−p)
n .
Also ist nach
n→∞
Beispiel. Uns interessiert, wie viele Versuche zu einer Zufallssituation durchgeführt werden
müssen, damit mit einer Wahrscheinlichkeit von mindestens 95 % die relative Häufigkeit Hn (A)
und die Wahrscheinlichkeit p = P (A) eines Ereignisses A bis zwei Stellen nach dem Komma
übereinstimmen. Wir setzen also ε = 0,005 und erhalten mit p(1 − p) = −(p − 21 )2 + 41 ≤ 14
analog zum obigen Beweis:
P (|Hn (A) − p| ≤ ε) > 1 −
p(1 − p)
1
10000
D2 (Hn (A))
.
=1−
≥1−
=1−
ε2
nε2
4nε2
n
Wenn für ein n die Gleichung 1 − 10000
= 0,95 erfüllt ist, so können wir also sicher sein, dass
n
P (|Hn (A) − p| ≤ ε) ≥ 0,95 gilt. Wir erhalten somit als Lösung n = 200000 (oder größer). Wie
wir weiter unten sehen werden, ist diese Abschätzung sehr grob.
1.4.2 Grenzverteilungssätze
1.4.2.1 Zentraler Grenzverteilungssatz
Das schwache Gesetz der großen Zahlen liefert nur eine Aussage über den stochastischen Grenzwert des arithmetischen Mittels X̄n einer Folge von Zufallsgrößen X1 , . . . , Xn . In vielen Anwendungen wird aber auch die Grenzverteilung des standardisierten arithmetischen Mittels
X̄n − EX̄n
X̄n − µ
X̄n − µ √
Ȳn = √
=
=
n.
σ
√
σ
D2 X̄n
n
benötigt.
44
Satz 1.4.3 (Zentraler Grenzverteilungssatz von Lindeberg/Levy). Sei X̄n das arithmetische
Mittel einer Folge X1 , . . . , Xn von Zufallsgrößen vom Typ i.i.d., µ = EXi ∈ R und 0 < σ 2 =
√
D2 X < ∞. Weiter sei Fn (x) die Verteilungsfunktion der Zufallsgröße Ȳn = X̄nσ−µ n, d.h.
(
Fn (x) = P
X̄n − µ √
n<x
σ
)
(
=P
)
X1 + · · · + Xn − nµ
√
<x
nσ 2
für alle x ∈ R. Dann gilt für alle x ∈ R
lim Fn (x) = Φ(x),
n→∞
wobei Φ die Verteilungsfunktion der standardisierten Normalverteilung bezeichnet. Die Standardisierung Ȳn von X̄n ist also asymptotisch N(0, 1)-verteilt (Schreibweise: X̄n ≈ N(0, 1)).
Anwendung Das arithmetische Mittel einer Folge von Zufallsgrößen kann also in guter Näherung als normalverteilt angenommen werden. Somit motiviert der zentrale Grenzverteilungssatz
die Annahme, dass eine durch Überlagerung zahlreicher unabhängiger Einzeleinflüsse entstehende Zufallsgröße (z.B. Messfehler) als normalverteilt aufgefasst werden kann.
1.4.2.2 Grenzverteilungssatz von Moivre/Laplace
Wir betrachten nun einen Spezialfall des zentralen Grenzverteilungssatzes. Zu einer Zufallssituation werden n Versuche durchgeführt, wobei die Zufallsgrößen Xi angeben, ob das Ereignis A im
i-ten Versuch eingetreten ist (Xi = 1) oder nicht (Xi = 0). Wir setzen p = P (A) = P (Xi = 1)
und Yn = X1 +· · ·+Xn . Die Zufallsgröße Yn gibt also an, wie oft das Ereignis A bei n Versuchen
eingetreten ist. Es gilt Yn ∼ B(n, p) und somit EYn = np und D2 Yn = np(1 − p). Für genügend
n
= Ynn aus dem zentralen Grenzverteilungssatz die
große n erhalten wir mit X̄n = X1 +···+X
n
Beziehung
X̄n − p √
Yn − np
Yn − EYn
X̄n − EX̄n √
n= √
n= √
= √ 2
,
N(0, 1) ≈ √
D Yn
p(1 − p)
np(1 − p)
D2 X̄n
d.h. Yn ≈ N(np, np(1 − p)). Damit haben wir die Aussage des Grenzverteilungssatzes von
Moivre/Laplace hergeleitet.
Satz 1.4.4 (Grenzverteilungssatz von Moivre/Laplace). Sei X ∼ B(n, p) eine binomialverteilte Zufallsgröße und Fn (x) die Verteilungsfunktion der standardisierten Zufallsgröße
Y = √X−np . Dann gilt für alle x ∈ R
np(1−p)
lim Fn (x) = Φ(x),
n→∞
wobei Φ die Verteilungsfunktion der standardisierten Normalverteilung bezeichnet. Die binomialverteilte Zufallsgröße X ist also asymptotisch N (np, np(1 − p)) verteilt.
Faustregel Der Grenzverteilungssatz von Moivre/Laplace ist in guter Näherung anwendbar, wenn np(1 − p) > 9 gilt. Selbst für np(1 − p) > 4 erhält man noch eine brauchbare
Näherung.
45
Anwendung Die Berechnung von Wahrscheinlichkeiten ist bei binomialverteilten Zufallsgrößen extrem rechenaufwändig. Mit Hilfe des obigen Satzes kann man diese aufwändigen Rechnungen auf die einfacher handhabbare Normalverteilung zurückführen.
Beispiel. Nun haben wir eine weitere Möglichkeit zur Lösung des Problems aus dem vorhergehenden Beispiel. Gesucht war die Versuchsanzahl n, die benötigt wird, damit mit einer
Wahrscheinlichkeit von mindestens 95 % die relative Häufigkeit Hn (A) und die Wahrscheinlichkeit p = P (A) eines Ereignisses A bis zwei Stellen nach dem Komma übereinstimmen. Wir
suchen also ein n, so dass P (|Hn (A) − p| ≤ ε) ≥ 0,95 gilt, wobei ε = 0,005 ist. Unter Verwendung des Grenzverteilungssatzes von Moivre/Laplace und den Bezeichnungen aus dessen
Herleitung erhalten wir zunächst:
P (|Hn (A) − p| ≤ ε) = P (|X̄n − p| ≤ ε) = P (|Yn − np| ≤ nε)
(
)
Y − np nε
n
= P √
≤ √
np(1 − p) np(1 − p)
(
)
−nε
Yn − np
nε
=P √
≤√
≤√
np(1 − p)
np(1 − p)
np(1 − p)
)
(
)
( √
)
( √
√
− nε
nε
nε
−Φ √
= 2Φ √
− 1.
=Φ √
p(1 − p)
p(1 − p)
p(1 − p)
(
Es muss also 2Φ
√
√
√ nε
p(1−p)
)
(
− 1 ≥ 0,95 gelten, d.h. Φ
√
√ nε
p(1−p)
)
≥ 0,975. Dies ist äquivalent
zu √ nε ≥ 1,96. Da p(1 − p) = −(p − 12 )2 + 41 ≤ 14 , ist letztere Beziehung erfüllt, wenn
√ p(1−p)
2 nε ≥ 1,96 gilt. Als Ergebnis erhalten wir also n = 38416 (oder größer). Diese Abschätzung ist
deutlich besser als die vorhergehende, die wir mit Hilfe der Tschebyscheff’schen Ungleichung
erhalten hatten.
Methode der Stetigkeitskorrektur Mit der hier vorgestellten Methode erhält man bessere
numerische Ergebnisse bei Verwendung des Grenzverteilungssatzes von Moivre/Laplace zur
näherungsweisen Berechnung von Wahrscheinlichkeiten der Form P (a ≤ Yn ≤ b) einer binomialverteilten Zufallsgröße Yn ∼ B(n, p), wobei a und b positive ganze Zahlen sind. Es gilt also
Yn ≈ N(np, np(1 − p)). Die Idee der Methode der Stetigkeitskorrektur ist, die Grenze a um 12
zu verringern und b um 21 zu erhöhen. Wir erhalten also:
(
)
(
)
1
1
b
+
−
np
a
−
−
np
P (a ≤ Yn ≤ b) ≈ P (a − 12 ≤ Yn ≤ b + 21 ) = Φ √ 2
−Φ √ 2
.
np(1 − p)
np(1 − p)
Beispiel. Wir wollen nun die Verbesserung der Ergebnisse durch die Methode der Stetigkeitskorrektur an konkreten Zahlen demonstrieren. Sei dazu Yn ∼ B(100; 0,25), a = 15 und b = 30.
Da np(1 − p) = 18,75 > 9 gilt, ist der Grenzverteilungssatz von Moivre/Laplace in guter
Näherung anwendbar. Es gilt also Yn ≈ N(25; 18,75). Als exaktes, aber sehr rechenaufwändiges
Ergebnis erhalten wir:
P (15 ≤ Yn ≤ 30) =
)
30 (
∑
100
0,25k 0,75100−k = 0,8908.
k
k=15
46
Ohne Stetigkeitskorrektur liefert die standardisierte Normalverteilung:
(
)
(
)
15 − 25
30 − 25
P (15 ≤ Yn ≤ 30) ≈ Φ √
−Φ √
= 0,8645.
18,75
18,75
Unter Verwendung der Methode der Stetigkeitskorrektur erhalten wir:
(
)
(
)
14,5 − 25
30,5 − 25
P (14,5 ≤ Yn ≤ 30,5) ≈ Φ √
−Φ √
= 0,8903.
18,75
18,75
Wir sehen also deutlich, dass durch die Methode der Stetigkeitskorrektur eine bessere Näherung
erreicht wird.
1.4.2.3 Grenzverteilungssatz von Poisson
Wir haben bereits zur Herleitung der Wahrscheinlichkeitsfunktion der Poisson-Verteilung
einen Zusammenhang zwischen Binomial- und Poisson-Verteilung hergestellt. Allgemeiner erhalten wir den folgenden Satz.
Satz 1.4.5 (Grenzverteilungssatz von Poisson). Gegeben sei eine Folge von binomialverteilten
Zufallsgrößen Yn ∼ B(n, pn ) mit pn → 0 und npn → λ > 0 für n → ∞. Dann gilt
lim P (Yn = k) = πλ (k),
n→∞
d.h. die Zufallsgrößen Yn sind asymptotisch Poisson-verteilt mit dem Parameter λ.
Beweis. Es gilt
( )
n k
lim P (Yn = k) = lim
pn (1 − pn )n−k
n→∞
n→∞ k
n(n − 1) · · · (n − k + 1) (npn )k (
npn )n
1
= lim
1
−
k
k
n→∞
n
k!
n
(1
−
|
{z
} | {z } |
{z
} | {zpn ) }
→1
=
λk
k!
k
→ λk!
e−λ
→1
e−λ = πλ (k).
Faustregel Den Grenzverteilungssatz von Poisson kann man ohne Bedenken anwenden, wenn
die Ungleichungen np ≤ 10 und 1500p ≤ n erfüllt sind.
Anwendung Wie der Grenzverteilungssatz von Moivre/Laplace, so verringert auch der
Grenzverteilungssatz von Poisson den Rechenaufwand bei einer binomialverteilten Zufallsgröße erheblich. Sollte der Parameter p der Binomialverteilung zu klein sein, um mit dem
Grenzverteilungssatz von Moivre/Laplace eine ausreichend gute Näherung zu erzielen, so
kann der Grenzverteilungssatz von Poisson genutzt werden.
Beispiel. Für eine binomialverteilte Zufallsgröße X ∼ B(100; 0,01) soll die Wahrscheinlichkeit
P (2 ≤ X ≤ 10) berechnet werden. Wegen np(1 − p) = 0,99 < 4 sollte der Grenzverteilungssatz von Moivre/Laplace nicht genutzt werden. Jedoch liefert der Grenzverteilungssatz von
47
Poisson eine gute Näherung, da np = 1 ≤ 10 und 1500p = 15 ≤ 100 = n. Wir erhalten somit
als Näherung
10
∑
P (2 ≤ X ≤ 10) =
π1 (k) = 0,264241.
k=2
Exakte Rechnung ergibt
)
10 (
∑
100
P (2 ≤ X ≤ 10) =
0,01k 0,99100−k = 0,264238.
k
k=2
1.4.2.4 Bemerkung zur hypergeometrischen Verteilung
Es lassen sich auch Grenzverteilungssätze für eine hypergeometrisch verteilte Zufallsgröße X ∼
H(n, N, M ) formulieren. Wenn z.B. N → ∞, M → ∞ und M
N → p für n → ∞ gilt, so nutzt
man die Näherung
(M )(N −M ) ( )
n k
P (X = k) = k (Nn−k
≈
p (1 − p)n−k ,
)
k
n
d.h man ersetzt die hypergeometrische Verteilung näherungsweise durch eine entsprechende
Binomialverteilung. Es gibt jedoch keine handhabbaren Faustregeln für die Nutzung dieser
Approximation. Um die so erhaltene Binomialverteilung auszuwerten, kann man dann den
Grenzverteilungssatz von Moivre/Laplace oder den Grenzverteilungssatz von Poisson verwenden.
1.5 Mehrdimensionale Verteilungen
Bisher wurden ausschließlich reellwertige, d.h. eindimensionale, Zufallsgrößen betrachtet. Wir
haben also stets nur ein Merkmal des zu beobachtenden Objekts bei unseren Untersuchungen
berücksichtigt. Häufig sind aber bei praktischen Modellierungsproblemen mehrere Merkmale
der Beobachtungsobjekte gleichermaßen von Interesse. Somit benötigen wir mehrdimensionale
Zufallsgrößen.
1.5.1 Einführung
Definition 1.5.1. Sei X = (X1 , X2 , . . . , Xn ) eine Zusammenfassung von n Zufallsgrößen
X1 , X2 , . . . , Xn . Dann heißt das Objekt X n-dimensionale Zufallsgröße oder zufälliger Vektor.
Definition 1.5.2. Die durch
F (x1 , . . . , xn ) := P (X1 < x1 , . . . , Xn < xn )
für alle Vektoren (x1 , . . . , xn ) ∈ Rn definierte reelle Funktion F heißt Verteilungsfunktion des
zufälligen Vektors X = (X1 , . . . , Xn ).
Wir werden im Folgenden nicht immer den allgemeinen Fall X = (X1 , . . . , Xn ) betrachten,
sondern uns auf n = 2, d.h. X = (X, Y ), beschränken, wenn dies das Verständnis erleichtert.
Ein Großteil der Aussagen gilt dann analog für allgemeines n.
48
Definition 1.5.3. Für einen zufälligen Vektor X = (X, Y ) heißen die Funktionen
FX (x) := lim F (x, y)
y→∞
und
FY (y) := lim F (x, y)
x→∞
Randverteilung von X bzw. Y . Die zu einer Randverteilung gehörende Wahrscheinlichkeitsbzw. Dichtefunktion bezeichnen wir ebenfalls als Randverteilung.
Eigenschaften der Verteilungsfunktion
• 0 ≤ F (x, y) ≤ 1 ∀x, y ∈ R.
•
lim F (x, y) = 0 ∀y ∈ R,
x→−∞
lim F (x, y) = 0 ∀x ∈ R.
y→−∞
• Die Randverteilungen FX und FY sind die Verteilungsfunktionen der eindimensionalen
Zufallsgrößen X und Y , d.h.
FX (x) = P (X < x) ∀x ∈ R
und
FY (y) = P (Y < y) ∀y ∈ R.
• x→∞
lim F (x, y) = 1.
y→∞
• F (x, y) ist in beiden Komponenten monoton wachsend, d.h.
x1 < x2 ⇒ F (x1 , y) ≤ F (x2 , y) ∀y ∈ R,
y1 < y2 ⇒ F (x, y1 ) ≤ F (x, y2 ) ∀x ∈ R.
• F (x, y) ist in beiden Komponenten linksseitig stetig, d.h.
lim F (x − h, y) = F (x, y) = lim F (x, y − h) ∀x, y ∈ R.
h→0
h>0
h→0
h>0
1.5.1.1 Kovarianz und Korrelationskoeffizient
Für einen zufälligen Vektor (X, Y ) bezeichnen wir mit µX := EX den Erwartungswert und mit
2 := D2 X die Varianz der Randverteilung von X. Analog µ := EY und σ 2 := D2 Y für die
σX
Y
Y
Randverteilung von Y .
Definition 1.5.4. Seien X und Y zwei Zufallsgrößen. Dann heißt die Größe
σXY := Cov(X, Y ) := E(X − EX)(Y − EY )
Kovarianz der Zufallsgrößen X und Y . Die Kovarianz ist ein Maß für das stochastische Verhalten der Zufallsgrößen zueinander. Die Zufallsgrößen X und Y heißen unkorreliert, wenn
Cov(X, Y ) = 0 gilt.
Eigenschaften der Kovarianz
• Cov(X, Y ) = E(XY ) − EXEY = Cov(Y, X),
• Cov(a + bX, c + dY ) = bdCov(X, Y ),
49
• Cov(X, X) = D2 X.
Satz 1.5.5. Existieren die zweiten Momente der Randverteilungen von X und Y , so existiert
auch die Kovarianz Cov(X, Y ).
Definition 1.5.6. Besitzen die beiden Zufallsgrößen X und Y endliche Streuungen, so heißt
die Größe
σXY
ρXY :=
σX σY
Korrelationskoeffizient von X und Y .
Satz 1.5.7. Für den Korrelationskoeffizienten zweier Zufallsgrößen X und Y gilt
−1 ≤ ρXY = ρY X ≤ 1.
Der Korrelationskoeffizient ρXY zweier Zufallsgrößen X und Y ist also ein normiertes Maß
für das stochastische Verhalten beider Zufallsgrößen zueinander. X und Y sind offensichtlich
genau dann unkorreliert, wenn ρXY = 0 gilt. ρXY ≈ −1 drückt starke negative Korrelation und
ρXY ≈ 1 starke positive Korrelation aus.
1.5.1.2 Diskrete Verteilungen
Definition 1.5.8. Ein zufälliger Vektor X = (X1 , . . . , Xn ) heißt diskret verteilt, wenn alle
eindimensionalen Randverteilungen diskrete Verteilungen sind.
Die Komponenten eines diskret verteilten zufälligen Vektors X = (X1 , . . . , Xn ) nehmen die
Werte X1 = x1i1 , . . . , Xn = xnin an, wobei für endliches Xj ij ∈ {1, . . . , lj } =: IXj mit lj ∈ N
und für abzählbar unendliches Xj ij ∈ N =: IXj gilt. Die Wahrscheinlichkeitsfunktion von X
lässt sich als n-dimensionales Feld schreiben:
pi1 ...in = P (X1 = x1i1 , . . . , Xn = xnin ).
Im Fall n = 2 bezeichnen wir die Werte der beiden Komponenten X und Y des zufälligen
Vektors X mit xj und yk , wobei j ∈ IX und k ∈ IY . Die Wahrscheinlichkeitsfunktion von X
lässt sich dann als endliche oder unendliche Matrix mit Einträgen der Form
pjk = P (X = xj , Y = yk )
schreiben. Für die Randverteilungen von X und Y erhalten wir
∑
∑
pj· =
pjk
und
p·k =
pjk .
j∈IX
k∈IY
Für Erwartungswert, Varianz und Kovarianz von X und Y gilt:
∑
∑
• EX = µX =
xj pj· ,
EY = µY =
yk p·k ,
j∈IX
2 =
• D2 X = σX
∑
k∈IY
(xj − µX )2 pj· ,
j∈IX
• Cov(X, Y ) = σXY =
∑ ∑
D2 Y = σY2 =
∑
k∈IY
(xj − µX )(yk − µY )pjk .
j∈IX k∈IY
50
(yk − µY )2 p·k ,
Beispiel. In einer Urne befinden sich 12 Lose: 2 Geldgewinne, 4 Freilose und 6 Nieten. Es
werden ohne Zurücklegen 2 Lose gezogen. Wir bezeichnen mit X die Anzahl der gezogenen
Geldgewinne und mit Y die Anzahl der gezogenen Freilose. Gesucht werden die Wahrscheinlichkeitsfunktion pjk = P (X = xj , Y = yk ) des zufälligen Vektors (X, Y ) und die zugehörigen
Randverteilungen pj· und p·k seiner Komponenten X und Y . Aus kombinatorischen Überlegungen ergibt sich:
 2 4
6
 (xj )(yk )(2−xj −yk )
, 0 ≤ x j + yk ≤ 2
(12
pjk =
.
2)

0,
x j + yk > 2
Die Wahrscheinlichkeitsfunktion lässt sich zusammen mit den Randverteilungen wie folgt als
Tabelle darstellen:
0
yj
5
22
4
11
1
11
15
22
0
1
2
pj· →
xk
1
2
11
4
33
p·k
↓
2
1
66
0
0
0
10
33
1
66
∑
14
33
16
33
1
11
=1
Die Randverteilung pj· bzw. p·k von X bzw. Y erhält man dabei aus den Spalten- bzw. Zeilensummen der 3 × 3-Matrix. Da die Randverteilungen eindimensionale Wahrscheinlichkeitsfunktionen sind, sind die Summen der Werte der Randverteilungen stets 1.
1.5.1.3 Stetige Verteilungen
Definition 1.5.9. Ein zufälliger Vektor X = (X1 , . . . , Xn ) heißt stetig verteilt mit der Verteilungsfunktion F , wenn es eine integrierbare Dichtefunktion f gibt mit
∫x1
∫xn
···
F (x1 , . . . , xn ) = P (X1 < x1 , . . . , Xn < xn ) =
−∞
f (t1 , . . . , tn ) dt1 · · · dtn .
−∞
Definition 1.5.10. Sei g eine reelle Funktion von n reellen Veränderlichen und sei X =
(X1 , . . . , Xn ) eine stetig verteilte n-dimensionale Zufallsgröße. Dann ist der Erwartungswert
Eg(X) gegeben durch
∫∞
∫∞
···
Eg(X) :=
−∞
g(x1 , . . . , xn )f (x1 , . . . , xn ) dx1 · · · dxn .
−∞
Definition 1.5.11. Sei (X, Y ) ein stetig verteilter zufälliger Vektor und f seine Dichtefunktion.
Dann heißen die Funktionen
∫∞
fX (x) =
∫∞
f (x, y) dy
und
−∞
fY (y) =
f (x, y) dx
−∞
Randdichten der Komponenten X und Y .
51
Die Randdichten sind eindimensionale Dichtefunktionen. Für Erwartungswert, Varianz und
Kovarianz von X und Y erhalten wir:
• EX = µX =
∫∞
−∞
2 =
• D2 X = σX
xfX (x) dx,
∫∞
−∞
EY = µY =
(x − µX )2 fX (x) dx,
• Cov(X, Y ) = σXY =
∫∞ ∫∞
−∞ −∞
∫∞
−∞
yfY (y) dy,
D2 Y = σY2 =
∫∞
−∞
(y − µY )2 fY (y) dy,
(x − µX )(y − µY )f (x, y) dx dy.
Beispiel. Als Beispiel für eine mehrdimensionale Verteilung betrachten wir die zweidimensionale Normalverteilung. Ein zufälliger Vektor (X, Y ) ist normalverteilt, wenn er die Dichtefunktion
(
[(
)2
(
)(
) (
)2 ])
x−µX
x−µX
y−µY
y−µY
−1
exp 2(1−ρ2 )
− 2ρ σX
+ σY
σX
σY
√
f (x, y) =
2πσX σY 1 − ρ2
mit den Parametern σX > 0, σY > 0 und −1 < ρ < 1 besitzt. Als Randdichten ergeben sich
die Funktionen
(
)
(
)
1
(x − µX )2
1
(y − µY )2
√
√
fX (x) =
exp −
und
fY (y) =
exp −
,
2
2σX
2σY2
2πσX
2πσY
d.h. die Randverteilungen sind eindimensionale Normalverteilungen. Der Parameter ρ = ρXY =
σXY
σX σY ist der Korrelationskoeffizient und somit ist Cov(X, Y ) = σXY = ρσX σY . Ist ρ = 0, so
sind X und Y also unkorreliert und für die Dichtefunktion f gilt die Produktdarstellung
(
)
1
(x − µX )2 (y − µY )2
f (x, y) =
exp −
−
= fX (x)fY (y).
2
2πσX σY
2σX
2σY2
1.5.1.4 Stochastische Unabhängigkeit
Definition 1.5.12. Zwei Zufallsgrößen X und Y heißen stochastisch unabhängig, wenn für den
zufälligen Vektor (X, Y ) gilt:
F (x, y) = FX (x)FY (y) ∀x, y ∈ R.
Bemerkung. Handelt es sich bei den stochastisch unabhängigen Zufallsgrößen X und Y um
diskrete Verteilungen, so gilt
pjk = pj· p·k ∀x, y ∈ R.
Im stetigen Fall gilt analog
f (x, y) = fX (x)fY (y) ∀x, y ∈ R.
Satz 1.5.13. Seien X und Y stochastisch unabhängige Zufallsgrößen mit D2 X < ∞ und
D2 Y < ∞. Dann gilt Cov(X, Y ) = 0, d.h. aus der stochastischen Unabhängigkeit folgt stets
die Unkorreliertheit.
52
Beweis (für stetige Zufallsgrößen). Da X und Y stochastisch unabhängig sind, gilt:
∫∞ ∫∞
(x − µX )(y − µY )f (x, y) dx dy
Cov(X, Y ) =
−∞ −∞
∫∞ ∫∞
(x − µX )(y − µY )fX (x)fY (y) dx dy
=
−∞ −∞
∫∞
∫∞
(x − µX )fX (x) dx
=
−∞
(y − µY )fY (y) dx
−∞
= (E(X − µX ))(E(Y − µY )) = (µX − µX )(µY − µY ) = 0
Wie wir am vorhergehenden Beispiel gesehen haben, folgt im Falle einer zweidimensionalen Normalverteilung aus der Unkorreliertheit der beiden Komponenten deren stochastische
Unabhängigkeit. Zusammen mit dem vorhergehenden Satz erhalten wir also die nachfolgende
Aussage.
Satz 1.5.14. Sei (X, Y ) ein (zweidimensional) normalverteilter zufälliger Vektor. Dann sind
die Komponenten X und Y genau dann stochastisch unabhängig, wenn sie unkorreliert sind.
1.5.2 Bedingte Verteilungen
In diesem Abschnitt betrachten wir nur den Fall n = 2, d.h. zufällige Vektoren der Form
X = (X, Y ). X und Y seien dabei stetig verteilte Zufallsgrößen.
Bei bedingten Verteilungen wird nur eine der beiden Komponenten eines zufälligen Vektors
betrachtet, d.h. die andere Komponente bleibt konstant. Wir erhalten also z.B. Aussagen über
die Verteilung der Zufallsgröße X, wenn Y einen festen Wert hat.
Definition 1.5.15. Seien X und Y stetig verteilte Zufallsgrößen mit den Randdichten fX und
fY , wobei fX (x) > 0 und fY (y) > 0 für alle x, y ∈ R. Dann heißen die Funktionen
fX|Y =y (x) =
f (x, y)
fY (y)
und
fY |X=x (y) =
f (x, y)
fX (x)
bedingte Dichten.
Bemerkung. fX|Y =y (x) ist eine eindimensionale Dichtefunktion, da fX|Y =y (x) ≥ 0 und
∫∞
∫∞
fX|Y =y (x) dx =
−∞
−∞
f (x, y)
1
dx =
fY (y)
fY (y)
∫∞
f (x, y) dx =
−∞
fY (y)
= 1.
fY (y)
fX|Y =y ist also die Dichtefunktion der Zufallsgröße X unter der Bedingung Y = y. Analoges
gilt für fY |X=x (y)
53
Definition 1.5.16. Die Größe
∫∞
E(X|Y = y) =
xfX|Y =y (x) dx
−∞
heißt bedingter Erwartungswert der Zufallsgröße X unter der Bedingung, dass Y den Wert y
annimmt.
Beispiel. Wir betrachten nochmals einen normalverteilten Zufallsvektor (X, Y ). Als bedingte
Dichte haben wir

(
) 2 

σX
f (x, y)
1
 1 x − µX + ρ σY (y − µY )  
√
√
exp − 
fX|Y =y (x) =
=√
.
fY (y)
2
2πσX 1 − ρ2
σX 1 − ρ2
Daraus ergibt sich der bedingte Erwartungswert
E(X|Y = y) = µX + ρ
σX
(y − µY ).
σY
Die Gerade x = E(X|Y = y) heißt Regressionsgerade im (x, y)-Koordinatensystem und gibt
für jedes y den Wert (x, y) des Zufallsvektors an, für den X den Erwartungswert unter der
Bedingung Y = y annimmt. Ist ρ = 0, d.h. X und Y sind unkorreliert und damit stochastisch
unabhängig, so ist die Regressionsgerade x = µx parallel zur y-Achse und es gilt fX|Y =y (x) =
fX (x).
1.5.3 Erwartungswertevektor, Kovarianzmatrix, Normalverteilung
Da wir in diesem Abschnit mit Matrizen rechnen, schreiben wir Vektoren immer als Spaltenvektoren. Wir betrachten den n-dimensionalen Fall, d.h.
 
X1
 .. 
X =  . .
Xn
Definition 1.5.17. Den Vektor

 

µ1
EX1
  

µ = EX =  ...  =  ... 
µn
EXn
der Erwartungswerte der Komponenten X1 , . . . , Xn eines zufälligen Vektors X nennen wir Erwartungswertevektor von X.
Definition 1.5.18. Sei X ein zufälliger Vektor mit den Komponenten X1 , . . . , Xn . Dann heißt
die Matrix
(
)
Σ = CovX = Cov(Xi , Xj )
= E(X − EX)(X − EX)T
i,j=1...n
Kovarianzmatrix von X.
54
Satz 1.5.19. Existiert die Kovarianzmatrix Σ des Zufallsvektors X, so ist sie symmetrisch,
d.h. Σ = ΣT , und positiv semidefinit, d.h. für alle v ∈ Rn gilt ⟨Σ v, v⟩ = v T Σ v ≥ 0.
Beweis. Die Symmetrie der Kovarianzmatrix folgt direkt aus Cov(Xi , Xj ) = Cov(Xj , Xi ) und
es gilt
(
)
(
)2
v T Σ v = v T E(X − EX)(X − EX)T v = E v T (X − EX) ≥ 0.
Definition 1.5.20. Ein Zufallsvektor X mit den Komponenten X1 , . . . , Xn heißt nichtsingulär
n-dimensional normalverteilt mit den Parametern µ = EX und Σ = Cov(X), geschrieben
X ∼ N(µ, Σ), wenn Σ symmetrisch und positiv definit ist und die Dichtefunktion f die Form
√
f (x) =
|Σ−1 |
(2π)
n
2
(
)
exp − 21 (x − µ)T Σ−1 (x − µ)
besitzt, wobei |Σ−1 | die Determinante der Inversen der Kovarianzmatrix bezeichnet.
Falls für X ∼ N(µ, Σ) die Komponenten Xi ∼ N(µi , σi2 ) paarweise disjunkt sind, d.h.


Σ=
σ12
0
..
so gilt
|Σ−1 | =
1
σ1 ···σn

,
σn2
0
√
.

und
(
)
1
(xi − µi )2
√
f (x) =
exp −
.
2σi2
2πσi
i=1
n
∏
Die Dichte f des Zufallsvektors X ist also in diesem Fall gleich dem Produkt der Randdichten
seiner Komponenten Xi .
55
2 Einführung in die mathematische Statistik
Die Hauptaufgabe der mathematischen Statistik ist es, anhand der Eigenschaften eines Teils
einer Menge von Objekten auf die Eigenschaften aller Objekte in dieser Menge zu schließen.
Diese Objekte können zum Beispiel Glühlampen sein und wir betrachten deren Lebensdauer.
Jeder Glühlampenhersteller möchte natürlich wissen, wie lang seine Glühlampen brennen. Um
dies exakt herauszubekommen, müsste man die Lebensdauer jeder Lampe bestimmen. Auf
Grund der hohen Anzahl (z.B. Tagesproduktion), aber auch weil die Glühlampen dabei zerstört
werden, ist dies nicht möglich. Stattdessen wählt man zufällig einige Glühlampen aus und
schließt aus deren Brenndauer mit Hilfe der Methoden der mathematischen Statistik auf die
durchschnittliche Lebensdauer. Weiter unten werden wir dieses Beispiel genauer betrachten.
2.1 Grundbegriffe
Grundgesamtheit: Eine Menge von gleichartigen Objekten, die hinsichtlich einer bestimmten
Eigenschaft untersucht werden sollen, nennen wir Grundgesamtheit. Diese Eigenschaft beschreiben wir dabei durch eine Zufallsgröße X. Die Verteilungsfunktion von X bezeichnen
wir mit Fϑ , d.h. Fϑ (x) = P (X < x), wobei ϑ für einen oder mehrere noch zu bestimmende
Parameter der Verteilung steht.
Stichprobe: Seien X1 , . . . , Xn n Realisierungen der Zufallsgröße X, d.h. X1 , . . . , Xn und X
sind unabhängig und weisen identische Verteilungen auf, kurz: sie sind vom Typ i.i.d.
Dann bezeichnen wir den zufälligen Vektor (X1 , . . . , Xn ) als Stichprobe vom Umfang n.
Auch ein konkreter Wert (x1 , . . . , xn ) ∈ Rn dieses Vektors wird als (konkrete) Stichprobe
bezeichnet.
Stichprobenraum: Sei (X1 , . . . , Xn ) eine Stichprobe vom Umfang n. Dann bezeichnen wir mit
Xn die Menge aller möglichen Werte dieses zufälligen Vektors. Diese Menge heißt Stichprobenraum und es gilt Xn ⊂ Rn .
Parameterraum: Die Menge aller möglichen Parameterwerte ϑ der Verteilungsfunktion Fϑ der
Zufallsgröße X heißt Parameterraum und wird mit Θ bezeichnet.
Stichprobenfunktion: Eine Funktion Tn : Xn → R heißt Stichprobenfunktion. Es handelt sich
also um eine Funktion, die einer konkreten Stichprobe eine reelle Zahl Tn (x1 , . . . , xn )
zuordnet.
Beispiel. Nachdem wir nun die grundlegenden Begriffe der mathematischen Statistik kennen,
wollen wir nochmals auf das obige Beispiel der Glühlampenproduktion eingehen. Als Grundgesamtheit betrachten wir die an einem festen Tag hergestellten Glühlampen. Deren zufällige Lebensdauer bezeichnen wir mit X. Uns interessiert nun, wie die Lebensdauer der Lampen verteilt
ist, d.h. wir suchen die Verteilungsfunktion Fϑ von X. Dazu wählen wir zufällig n Glühlampen
aus und bestimmen deren Lebensdauer, wir entnehmen also eine Stichprobe (X1 , . . . , Xn ) vom
56
Umfang n. Der Stichprobenraum Xn umfasst somit alle n-dimensionalen Vektoren mit nichtnegativen Komponenten. Ist die Art der Verteilung bekannt (z.B. X ∼ N(µ, σ 2 ) und somit
ϑ = (µ, σ 2 ) ∈ Θ = R × R), können wir den Parameter mit Hilfe einer konkreten Stichprobe
(x1 , . . . , xn ) schätzen. Wie dies genau funktioniert, behandeln wir weiter unten.
Beispiel. Als weiteres einführendes Beispiel betrachten wir analog zum obigen Beispiel die
Produktion von elektrischen Sicherungen. Als Grundgesamtheit wählen wir die Tagesproduktion
und untersuchen die Zufallsgröße
{
1, Sicherung defekt
X=
,
0, Sicherung funktioniert
deren Verteilungsfunktion Fϑ gesucht ist. X ∼ B(1, p) ist eine binomialverteilte Zufallsgröße
mit dem Parameter ϑ = p ∈ Θ = (0, 1), wobei p die Wahrscheinlichkeit für einen Defekt angibt.
Es ist also P (X = 1) = p und P (X = 0) = 1 − p. Als Stichprobenraum erhalten wir
{
}
Xn = (x1 , . . . , xn ) ∈ Rn : xi = 1 ∨ xi = 0 .
Ein Beispiel für eine Stichprobenfunktion ist das arithmetische Mittel X̄n = n1 (X1 + · · · + Xn ).
Im Folgenden bezeichnen wir mit ϑ̂ den Schätzwert eines Parameters ϑ. Um die Parameter
einer Verteilung zu schätzen, gibt es zwei grundlegende Herangehensweisen, die wir in den
folgenden Abschnitten behandeln werden:
Punktschätzung: Aus einer Stichprobe (x1 , . . . , xn ) wird ein konkreter Wert ϑ̂ für den Parameter ϑ berechnet.
Bereichsschätzung: Aus einer Stichprobe (x1 , . . . , xn ) werden zwei Zahlen U (x1 , . . . , xn ) und
O(x1 , . . . , xn ) berechnet, so dass für ein kleines gegebenes α der wirkliche Parameter ϑ
mit einer Wahrscheinlichkeit von 1 − α im Intervall [U (x1 , . . . , xn ), O(x1 , . . . , xn )], dem
sogenannten Konfidenz- oder Vertrauensintervall, liegt.
2.2 Punktschätzung
Eine Stichprobenfunktion Tn : Xn → Θ mit Werten im Parameterraum bezeichnen wir als
Schätzfunktion. Ziel der Punktschätzung ist es, auf Grundlage einer solchen Schätzfunktion für
den unbekannten Parameter ϑ ∈ Θ der Grundgesamtheit (genauer: der Verteilungsfunktion
der in Zusammenhang mit der Grundgesamtheit betrachteten Zufallsgröße X) einen möglichst
guten Schätzwert ϑ̂ = Tn (X1 , . . . , Xn ) zu bestimmen. Wann eine Schätzung „gut“ ist, müssen
wir noch näher untersuchen.
Häufig wird nicht der Parameter ϑ selbst geschätzt, sondern eine Funktion τ (ϑ). Für X ∼
N(µ, σ 2 ) und ϑ = (µ, σ 2 ) können wir zum Beispiel durch getrennte Betrachtung von µ = τ1 (ϑ)
und σ 2 = τ2 (ϑ) die Schätzung in die zwei Schätzprobleme τˆ1 (ϑ) und τˆ2 (ϑ) zerlegen.
Eine Schätzfunktion Tn für den Parameter ϑ ist als Funktion der einzelnen Komponenten
X1 , . . . , Xn einer Stichprobe (X1 , . . . , Xn ) selbst wieder eine Zufallsgröße. Somit können wir
den Erwartungswert ETn und die Varianz D2 Tn betrachten.
57
Definition 2.2.1. Eine Schätzfunktion Tn für eine Funktion τ (ϑ) des unbekannten Parameters
ϑ heißt erwartungstreu, wenn für jeden Parameterwert ϑ ∈ Θ gilt:
ETn = τ (ϑ).
Satz 2.2.2. Existieren in einer Grundgesamtheit X sowohl der Erwartungswert EX als auch
die Varianz D2 X und ist (X1 , . . . , Xn ) eine Stichprobe, so gilt:
a) Eine erwartungstreue Schätzfunktion für τ (ϑ) = EX ist
1∑
X̄n =
Xi .
n
n
i=1
b) Eine erwartungstreue Schätzfunktion für τ (ϑ) = D2 X ist
1 ∑
=
(Xi − X̄n )2 .
n−1
n
Sn2
i=1
Beweis.
a) Es gilt
(
EX̄n = E
1∑
Xi
n
n
)
1∑
1
=
EXi = · n · EX = EX = τ (ϑ).
n
n
n
i=1
i=1
b) Für i = 1, . . . , n gilt
E(Xi − X̄n )2 = E(Xi − X̄n − (EX − EX))2 = E(Xi − X̄n − (EXi − X̄n ))2
= E(Xi − X̄n − E(Xi − X̄n ))2 = D2 (Xi − X̄n )
n
1 ∑ 2
n
n−1 2
= D2 Xi − 2
D Xk = D2 X − 2 D2 X =
D X
n
n
n
k=1
und somit ist
(
ESn2
=E
1 ∑
(Xi − X̄n )2
n−1
n
i=1
)
1 ∑
=
E(Xi − X̄n )2
n−1
n
i=1
1
n−1 2
=
·n·
D X = D2 X = τ (ϑ).
n−1
n
Bei der Konstruktion von Sn2 sind wir davon ausgegangen, dass der Erwartungswert EX
unbekannt ist. Sollte der Erwartungswert µ = EX jedoch bekannt sein, so kann man an Stelle
von Sn2 als Schätzfunktion für τ (ϑ) = D2 X auch
1∑
(Xi − µ)2
n
n
Vn2 =
i=1
58
verwenden. Vn2 ist ebenfalls erwartungstreu (Beweis: Übung!).
Definition 2.2.3. Eine Schätzfunktion Tn für eine Funktion τ (ϑ) des unbekannten Parameters
ϑ heißt konsistent, wenn für alle ϑ ∈ Θ und beliebig kleines reelles ε > 0 gilt:
lim = P (|Tn (X1 , . . . , Xn ) − ϑ| > ε) = 0.
n→∞
Satz 2.2.4. Die Schätzfunktion X̄n für τ (ϑ) = EX ist konsistent. Gilt EX 4 < ∞, so ist auch
die Schätzfunktion Sn2 für τ (ϑ) = D2 X konsistent.
Bemerkung. Für X̄n folgt die Behauptung unmittelbar aus dem Gesetz der großen Zahlen. Für
normalverteiltes X ∼ N(µ, σ 2 ) ist EX 4 < ∞ erfüllt.
Definition 2.2.5. Besitzt die erwartungstreue Schätzfunktion Tn unter allen erwartungstreuen
Schätzfunktionen für τ (ϑ) die kleinste Varianz, so heißt Tn wirksamste Schätzfunktion.
Satz 2.2.6. Ist X ∼ N(µ, σ 2 ) normalverteilt, so ist X̄n die wirksamste Schätzfunktion für
τ (ϑ) = EX.
2.3 Verteilungen wichtiger Stichprobenfunktionen
Bevor wir einige wichtige Stichprobenfunktionen betrachten, führen wir zunächst neben den
schon bekannten stetigen Verteilungen Gleich-, Exponential- und Normalverteilung noch drei
weitere stetige Verteilungen und den Begriff des Quantils ein.
2.3.1 Quantile
Definition 2.3.1. Sei X eine stetige Zufallsgröße mit der Dichtefunktion f und α ∈ (0, 1).
Dann heißt die Zahl qα α-Quantil zur Zufallsgröße X, wenn gilt:
∫qα
f (x) dx = α.
−∞
Bemerkung. α-Quantile werden in der Literatur manchmal auch als α-Fraktile bezeichnet. Zudem sind in einigen Büchern und Tabellen die Größen qα und q1−α vertauscht.
Beispiel. Für α = 0,5 ist das α-Quantil q0,5 gleich dem Median der Zufallsgröße X, d.h. es gilt
P (X < q0,5 ) = P (X > q0,5 ).
Im Fall einer symmetrischen Verteilung liegt der Median auf der Symmetrieachse.
Bemerkung. Das α-Quantil der Normalverteilung wird mit zα bezeichnet.
59
2.3.2 Weitere stetige Verteilungen
2.3.2.1 χ2 -Verteilung
Zur Definition der χ2 -Verteilung (Chi-Quadrat-Verteilung) benötigen wir die Gammafunktion
∫∞
Γ(x) =
tx−1 e−t dt.
0
Für n = 0, 1, 2, . . . gilt Γ(n + 1) = n!.
Definition 2.3.2. Besitzt die stetige Zufallsgröße X die Dichtefunktion

0,
x≤0
n
x
fn (x) =
,
1
−1
−
 n n x2 e 2, x > 0
2 2 Γ( 2 )
so nennen wir X χ2 -verteilt mit n Freiheitsgraden oder kurz χ2n -verteilt und schreiben X ∼ χ2n .
fn (x)
0
x
Bemerkung. Die α-Quantile der χ2 -Verteilung werden mit χ2n,α bezeichnet.
Die χ2 -Verteilung wird später bei der Bestimmung der Varianz einer normalverteilten Zufallsgröße eine wichtige Rolle spielen.
60
2.3.2.2 t-Verteilung
Definition 2.3.3. Besitzt die stetige Zufallsgröße X die Dichtefunktion
Γ( n+1
2 )
√
fn (x) =
Γ( n2 ) πn
(
)− n+1
2
x2
1+
,
n
so nennen wir X t-verteilt mit n Freiheitsgraden und schreiben X ∼ tn . Die t-Verteilung wird
auch als Student-Verteilung 1 bezeichnet.
fn (x)
x
0
Bemerkung. Die α-Quantile der t-Verteilung werden mit tn,α bezeichnet.
Die t-Verteilung wird später bei der Bestimmung des Erwartungswertes einer normalverteilten Zufallsgröße eine wichtige Rolle spielen.
2.3.2.3 F-Verteilung
Zur Definition der F-Verteilung benötigen wir die Betafunktion
∫1
ta−1 (1 − t)b−1 dt =
B(a, b) =
Γ(a)Γ(b)
.
Γ(a + b)
0
Für k, l ∈ N gilt B(k, l) =
(k−1)!(l−1)!
(k+l−1)! .
Definition 2.3.4. Besitzt die stetige Zufallsgröße X die Dichtefunktion

0,
x≤0
fm,n (x) = ( m ) m2 ·x m2 −1 (
,
m+n
)
− 2
m
 n m n
1
+
x
,
x
>
0
n
B( , )
2
2
so nennen wir X F-verteilt mit den Parametern m und n und schreiben X ∼ Fm,n . Die
F-Verteilung wird auch als Fisher’sche Verteilung bezeichnet.
1
Diese Verteilung wurde vom Mathematiker Gosset unter dem Pseudonym Student veröffentlicht
61
fn (x)
0
x
Bemerkung. Die α-Quantile der F-Verteilung werden mit Fm,n,α bezeichnet und es gilt
Fm,n,α =
1
Fm,n,1−α
.
2.3.3 Stichprobenfunktionen bei binomialverteilter Grundgesamtheit
Im Folgenden sei X ∼ B(1, p) eine binomialverteilte Grundgesamtheit und (X1 , . . . , Xn ) eine
Stichprobe. Xi und X sind also Zufallsgrößen vom Typ i.i.d. für i = 1, . . . , n. Dann gilt
Tn(0) =
n
∑
Xi ∼ B(n, p)
i=1
(0)
und für hinreichend großes n ist nach dem Grenzverteilungssatz von Moivre/Laplace Tn ≈
N(np, np(1 − p)) und somit
(
)
n
1∑
p(1 − p)
Xi ≈ N p,
.
n
n
Tn(1) = X̄n =
i=1
(1)
Durch Standardisierung von Tn
erhalten wir
X̄n − p √
Tn(2) = √
n ≈ N(0, 1).
p(1 − p)
2.3.4 Stichprobenfunktionen bei normalverteilter Grundgesamtheit
Sei X ∼ N(µ, σ 2 ) eine normalverteilte Grundgesamtheit und (X1 , . . . , Xn ) eine Stichprobe. Xi
und X sind also Zufallsgrößen vom Typ i.i.d. für i = 1, . . . , n. Dann gilt
X̄n =
(
)
n
1∑
σ2
Xi ∼ N µ,
n
n
i=1
und durch Standardisierung erhalten wir
Tn(3) =
X̄n − µ √
n ≈ N(0, 1).
σ
62
Weiter gilt
Tn(4) =
n
1 ∑
(Xi − µ)2 ∼ χ2n
σ2
i=1
und
Tn(5) =
Mit Sn =
√
n
(n − 1)Sn2
1 ∑
2
(X
−
X̄
)
=
∼ χ2n−1 .
i
n
σ2
σ2
i=1
Sn2 ist
Tn(6) = √
√
X̄n − µ
X̄n − µ √
n=
n ∼ tn−1
∑
n
Sn
1
2
(X
−
X̄
)
i
n
i=1
n−1
Allgemein gilt für stochastisch unabhängige Zufallsgrößen X ∼ N(0, 1) und Y ∼ χ2n
X
Tn(7) = √ ∼ tn .
Y
n
Sind X ∼ N(µ1 , σ12 ) und Y ∼ N(µ2 , σ22 ) stochastisch unabhängige, normalverteilte Grundgesamtheiten und (X1 , . . . , Xn1 ) und (Y1 , . . . , Yn2 ) entsprechende Stichproben, so ist
Tn1 ,n2 =
σ22 Sn21
∼ Fn1 −1,n2 −1 .
σ12 Sn22
2.4 Bereichsschätzung
Ziel der Bereichsschätzung ist es, mit Hilfe einer Stichprobe (X1 , . . . , Xn ) zur Grundgesamtheit
X mit der Verteilungsfunktion Fϑ zwei Schätzfunktionen U : Xn → Θ und O : Xn → Θ für den
unbekannten Parameter ϑ ∈ Θ der Verteilung von X zu finden, so dass ϑ mit einer Wahrscheinlichkeit von mindestens 1 − α im Intervall [U (X1 , . . . , Xn ), O(X1 , . . . , Xn )], dem sogenannten
Konfidenz- oder Vertrauensintervall, liegt. Dabei heißt die Zahl α ∈ (0, 1) Irrtumswahrscheinlichkeit und der Wert 1 − α heißt Konfidenzniveau. Als Formel ausgedrückt soll also gelten:
(
)
P U (X1 , . . . , Xn ) ≤ ϑ ≤ O(X1 , . . . , Xn ) ≥ 1 − α.
Die Irrtumswahrscheinlichkeit α ist dabei stets vorzugeben. Typische Werte sind zum Beispiel
α = 0,05 und α = 0,01.
2.4.1 Konfidenzintervalle bei binomialverteilter Grundgesamtheit
Im Folgenden sei X ∼ B(1, p) eine mit dem Parameter ϑ = p = P (X = 1) ∈ Θ = (0, 1) binomialverteilte Grundgesamtheit und (X1 , . . . , Xn ) eine Stichprobe. Wir suchen nun die Grenzen eines Konfidenzintervalls für das Konfidenzniveau 1 − α. Dazu nutzen wir die für hin(2)
reichend großes n standardnormalverteilte Stichprobenfunktion Tn ≈ N(0, 1) aus Abschnitt
2.3.3 und das Quantil z1−α/2 der Standardnormalverteilung. Unter Verwendung der Beziehung
63
Φ(za−α/2 ) = 1 −
(
P
−z1−α/2
α
2
ergibt sich daraus zunächst
X̄n − p √
n ≤ z1−α/2
≤√
p(1 − p)
)
= Φ(z1−α/2 ) − Φ(−z1−α/2 ) = 2Φ(z1−α/2 ) − 1 = 1 − α.
Durch Umrechnung in die Form
(
)
P U (X1 , . . . , Xn ) ≤ p ≤ O(X1 , . . . , Xn ) = 1 − α
erhalten wir für die Grenzen des Konfidenzintervalls:
]
[
√
2
z1−α/2
n
X̄n (1 − X̄n ) ( z1−α/2 )2
,
U (X1 , . . . , Xn ) =
X̄n +
− z1−α/2
+
2
2n
n
2n
n + z1−α/2
[
]
√
2
z1−α/2
n
X̄n (1 − X̄n ) ( z1−α/2 )2
O(X1 , . . . , Xn ) =
X̄n +
+ z1−α/2
+
.
2
2n
n
2n
n + z1−α/2
Beispiel. Aus der laufenden Produktion von Sicherungen wird eine Stichprobe vom Umfang
n = 100 entnommen und überprüft. Dabei erweisen sich 2 Sicherungen als defekt, also ist
2
p̂ = X̄n = 100
= 0,02. Gesucht wird ein Konfidenzintervall zum Konfidenzniveau 1 − α =
0,95. Aus einer Tabelle entnehmen wir z1−α/2 = z0,975 = 1,96 und somit erhalten wir durch
Einsetzen in die beiden Formeln das Intervall [0,0055; 0,0700]. Bei einer Stichprobe vom Umfang
n = 1000 mit 20 defekten Sicherungen ist p = X̄n = 0,02 und für 1 − α = 0,95 ergibt sich das
Konfidenzintervall [0,0130; 0,0304]. Wir sehen, dass mit steigendem n die Länge des Intervalls
abnimmt, d.h. je größer die Stichprobe, desto genauer die Schätzung.
2.4.2 Konfidenzintervalle bei normalverteilter Grundgesamtheit
Im Folgenden sei X ∼ N(µ, σ 2 ) eine normalverteilte Grundgesamtheit und (X1 , . . . , Xn ) eine
Stichprobe. Wir suchen Konfidenzintervalle zum Konfidenzniveau 1−α für die beiden Parameter
µ und σ 2 der Normalverteilung.
2.4.2.1 Konfidenzintervall für µ bei bekanntem σ 2
(3)
Wir verwenden die aus Abschnitt 2.3.4 bekannte Stichprobenfunktion Tn
Quantil z1−α/2 der Standardnormalverteilung. Aus
P
ergibt sich dann
mit
∼ N(0, 1) und das
(
)
X̄n − µ √
n ≤ z1−α/2 = 1 − α
−z1−α/2 ≤
σ
(
)
P U (X1 , . . . , Xn ) ≤ µ ≤ O(X1 , . . . , Xn ) = 1 − α
σ
U (X1 , . . . , Xn ) = X̄n − z1−α/2 √ ,
n
σ
O(X1 , . . . , Xn ) = X̄n + z1−α/2 √ .
n
64
2.4.2.2 Konfidenzintervall für µ bei unbekanntem σ 2
Der Parameter σ 2 sei unbekannt und mittels Sn2 geschätzt. Wir verwenden die aus Abschnitt
(6)
2.3.4 bekannte Stichprobenfunktion Tn ∼ tn−1 und das Quantil tn−1,1−α/2 der t-Verteilung.
Aus
(
)
X̄n − µ √
P −tn−1,1−α/2 ≤
n ≤ tn−1,1−α/2 = 1 − α
Sn
ergibt sich dann
(
)
P U (X1 , . . . , Xn ) ≤ µ ≤ O(X1 , . . . , Xn ) = 1 − α
mit
Sn
U (X1 , . . . , Xn ) = X̄n − tn−1,1−α/2 √ ,
n
Sn
O(X1 , . . . , Xn ) = X̄n + tn−1,1−α/2 √ .
n
2.4.2.3 Konfidenzintervall für σ 2 bei bekanntem µ
(4)
Wir verwenden die aus Abschnitt 2.3.4 bekannte Stichprobenfunktion Tn ∼ χ2n und die Quantile χn,1−α/2 und χn,α/2 der χ2 -Verteilung. Aus
(
P
χn,α/2
n
1 ∑
≤ 2
(Xi − µ)2 ≤ χn,1−α/2
σ
)
=1−α
i=1
ergibt sich dann
(
)
P U (X1 , . . . , Xn ) ≤ σ 2 ≤ O(X1 , . . . , Xn ) = 1 − α
mit
U (X1 , . . . , Xn ) =
1
χ2n,1−α/2
n
∑
(Xi − µ) ,
2
O(X1 , . . . , Xn ) =
i=1
1
n
∑
χ2n,α/2
i=1
(Xi − µ)2 .
2.4.2.4 Konfidenzintervall für σ 2 bei unbekanntem µ
Der Parameter µ sei unbekannt und mittels X̄n geschätzt. Wir verwenden die aus Abschnitt
(5)
2.3.4 bekannte Stichprobenfunktion Tn ∼ χ2n−1 und die Quantile χn−1,1−α/2 und χn−1,α/2 der
χ2 -Verteilung. Aus
(
)
(n − 1)Sn2
P χn−1,α/2 ≤
≤ χn−1,1−α/2 = 1 − α
σ2
ergibt sich dann
(
)
P U (X1 , . . . , Xn ) ≤ σ 2 ≤ O(X1 , . . . , Xn ) = 1 − α
mit
U (X1 , . . . , Xn ) =
(n − 1)Sn2
,
χ2n−1,1−α/2
O(X1 , . . . , Xn ) =
65
(n − 1)Sn2
.
χ2n−1,α/2
2.4.3 Einseitige Konfidenzintervalle
In manchen Fällen sind nur einseitige Konfidenzintervalle gesucht, d.h. es interessiert die Wahrscheinlichkeit
(
)
(
)
P U (X1 , . . . , Xn ) ≤ ϑ = 1 − α
oder
P ϑ ≤ O(X1 , . . . , Xn ) = 1 − α.
Um solche einseitigen Konfidenzintervalle zu berechnen, nutzt man die Formel für die entsprechende Intervallgrenze mit α statt α2 .
2.5 Tests
Wir betrachten eine Grundgesamtheit X mit der uns unbekannten Verteilungsfunktion Fϑ und
eine entsprechende Stichprobe (X1 , . . . , Xn ). Sinn und Zweck von Tests ist es nun, anhand der
Stichprobe Aussagen über die Art der Verteilung der Grundgesamtheit (parameterfreie Tests)
oder, bei bekannter Verteilungsart, über den Parameter ϑ ∈ Θ der Verteilung (Parametertests)
zu überprüfen. Es wird also getestet, ob die aufgestellte Behauptung über die Grundgesamtheit bzw. über deren Verteilungsparameter in signifikanter Weise von den aus der Stichprobe
gewonnenen Informationen abweicht oder nicht. Daher heißen solche Tests auch Signifikanztests.
2.5.1 Allgemeines Schema für Parametertests
Jeder Parametertest wird nach dem folgenden Schema durchgeführt:
1. Wir formulieren unsere Behauptung über den unbekannten Parameter ϑ der Verteilung
der Grundgesamtheit X als sogenannte Nullhypothese H0 und stellen die entsprechende Alternativhypothese H1 auf; diese ist das Komplement der Nullhypothese H0 . Für
bekanntes ϑ0 kommen zum Beispiel die folgenden Hypothesen in Frage:
H0 : ϑ = ϑ0
H0 : ϑ ≤ ϑ0
H0 : ϑ ≥ ϑ0
und H1 : ϑ ̸= ϑ0 ,
und H1 : ϑ > ϑ0 ,
und H1 : ϑ < ϑ0 .
Wir möchten nun wissen, ob die Behauptung H0 mit den in der Stichprobe (X1 , . . . , Xn )
enthaltenen Informationen vereinbar ist oder ob wir H0 ablehnen müssen und somit H1
für richtig befinden.
2. Wir wählen eine sogenannte Irrtumswahrscheinlichkeit α. Dies ist die Wahrscheinlichkeit
dafür, dass H0 auf Grund der Stichprobe abgelehnt wird, obwohl H0 richtig ist.
3. Wir wählen eine Stichprobenfunktion Tn (Testfunktion), deren Verteilung bei Gültigkeit
von H0 bekannt ist. Mit Hilfe dieser Testfunktion erhalten wir in Form einer reellen
Zahl Informationen über die Stichprobe. (Im Folgenden werden wir für die Zufallsgröße
Tn (X1 , . . . , Xn ) und die konkreten Funktionswerte Tn (x1 , . . . , xn ) zur besseren Übersicht
kurz Tn schreiben.)
4. Wir wählen einen kritischen Bereich K für die Werte der Testfunktion Tn , so dass
PH0 (Tn ∈ K) ≤ α gilt. D.h. falls die Nullhypothese H0 richtig ist, soll die Wahrscheinlichkeit dafür, dass der Wert der Testfunktion im kritischen Bereich liegt, kleiner oder gleich
der Irrtumswahrscheinlichkeit sein.
66
5. Sollte für die konkrete, zum Zwecke des Tests entnommene Stichprobe der Funktionswert der Testfunktion Tn in den kritischen Bereich fallen, so müssen wir H0 ablehnen.
Andernfalls spricht die Stichprobe nicht gegen die Hypothese H0 . In Formeln:
• Tn ̸∈ K ⇒ H0 wird angenommen,
• Tn ∈ K ⇒ H0 wird abgelehmt.
Da das Ergebnis eines Parametertests nur auf Stichproben beruht, können die zwei folgenden
Fehler auftreten.
Fehler 1. Art: Die Hypothese H0 ist richtig, wird aber auf Grund der Stichprobe abgelehnt.
Die Wahrscheinlichkeit für diesen Fehler beträgt α.
Fehler 2. Art: Die Hypothese H0 ist falsch, wird aber nicht abgelehnt, da die Stichprobe für
H0 spricht. Die Wahrscheinlichkeit für das Auftreten dieses Fehlers ist im Allgemeinen
unbekannt.
2.5.2 Parametertests bei binomialverteilter Grundgesamtheit
Sei X ∼ B(1, p) eine mit dem Parameter p binomialverteilte Grundgesamtheit und sei der
Wert p0 gegeben. Als Beispiel für einen Parametertest möchten wir anhand einer Stichprobe
(X1 , . . . , Xn ) vom Umfang n die Hypothese
H0 : p ≤ p0
überprüfen. Die entsprechende Alternativhypothese ist H1 : p > p0 . α sei die Irrtumswahrscheinlichkeit. Eine geeignete Testfunktion ist die uns bereits bekannte Stichprobenfunktion
Tn(0) =
n
∑
Xi ∼ B(n, p).
i=1
Entscheidend für das Testergebnis ist nun die Wahrscheinlichkeit
PH0 (Tn(0)
≥ c) = 1 −
PH0 (Tn(0)
< c) = 1 −
c−1
∑
PH0 (Tn(0)
k=0
c−1 ( )
∑
n k
p (1 − p0 )n−k .
= k) = 1 −
k 0
k=0
Ist diese kleiner oder gleich α, so müssen wir H0 ablehnen; ist sie größer als α, so können wir
davon ausgehen, dass H0 richtig ist.
Beispiel. Wir betrachten nochmals die Produktion von Sicherungen, d.h. X ∼ B(1, p), wobei p
die Wahrscheinlichkeit für einen Defekt angibt. Unsere Hypothese sei H0 : p ≤ p0 mit p0 = 0,01.
Wir setzen α = 0,05 und entnehmen eine Stichprobe (x1 , . . . , x100 ) vom Umfang n = 100
(0)
mit c = Tn (x1 , . . . , x100 ) = 2; es sind also zwei Sicherungen defekt in unserer Stichprobe.
Sprechen zwei defekte Sicherungen bei 100 überprüften für unsere Hypothese H0 oder nicht?
Durch Einsetzen der gegebenen Werte in obige Gleichung erhalten wir
(
)
(
)
100
100
(0)
0
100
PH0 (Tn ≥ 2) = 1 −
0,01 · 0,99 −
0,011 · 0,9999 = 0,264238 > 0,05 = α.
0
1
67
Somit können wir die Hypothese p ≤ 0,01 als richtig annehmen. Analog können wir die Rechnung für Stichproben mit c = 3 oder c = 4 usw. durchführen. Ab c = 4 müssen wir die
Hypothese dann jedoch ablehnen.
Gehen wir nach dem oben beschriebenen allgemeinen Schema für Parametertests vor, so
können wir zum Test der drei Hypothesen




p
=
p
0
p ̸= p0

mit
H1 : p > p0
H0 : p ≤ p0




p < p0
p ≥ p0
bei hinreichend großem n die Testfunktion
X̄n − p0 √
Tn(2) = √
n ≈ N(0, 1)
p0 (1 − p0 )
und den kritischen Bereich


|Tn | > z1−α/2
K = Tn > z1−α


Tn < −z1−α
verwenden.
2.5.3 Parametertests bei normalverteilter Grundgesamtheit
Sei X ∼ N(µ, σ 2 ) eine normalverteilte Grundgesamtheit und (X1 , . . . , Xn ) eine Stichprobe und
sei die Irrtumswahrscheinlichkeit α vorgegeben. Wir betrachten im Folgenden Hypothesen über
den Erwartungswert µ bei bekannter und unbekannter Varianz σ 2 und über die Varianz bei unbekanntem Erwartungswert. Auf Hypothesen über die Varianz bei bekanntem Erwartungswert
gehen wir nicht ein.
2.5.3.1 Hypothesen über µ bei bekanntem σ 2
Sei σ 2 bekannt und der Wert µ0 vorgegeben. Wir testen drei verschiedene Nullhypothesen H0
mit der jeweiligen Alternativhypothese H1 :




̸ µ0
µ =
µ = µ0
und
H1 : µ > µ0 .
H0 : µ ≤ µ0




µ < µ0
µ ≥ µ0
Als Testfunktion wählen wir
Tn(3) (X1 , . . . , Xn ) =
X̄n − µ0 √
n ∼ N(0, 1).
σ
68
Als kritischer Bereich ergibt sich


{x : |x| > z1−α/2 }
K = {x : x > z1−α }


{x : x < −z1−α }
,
da gilt:

)
(
X̄n −µ0 √ 
n
≤
z
1
−
P

σ

 (
) 1−α/2
X̄n −µ0 √
n > z1−α
PH0 (Tn ∈ K) = P

( σ √
)


P X̄n −µ0 n < −z1−α
σ




2 − 2Φ(z1−α/2 )
α
= α
= α .




1 − Φ(z1−α )
α


1 − (Φ(zα/2 ) − Φ(−z1−α/2 ))
= 1 − Φ(z1−α )


Φ(−z1−α )
2.5.3.2 Hypothesen über µ bei unbekanntem σ 2
Sei σ 2 unbekannt und durch Sn2 geschätzt und der Wert µ0 vorgegeben. Wir testen drei verschiedene Nullhypothesen H0 mit der jeweiligen Alternativhypothese H1 :




µ ̸= µ0
µ = µ0
und
H1 : µ > µ0 .
H0 : µ ≤ µ0




µ < µ0
µ ≥ µ0
Als Testfunktion wählen wir
Tn(6) (X1 , . . . , Xn ) =
X̄n − µ0 √
n ∼ tn−1 .
Sn
Als kritischer Bereich ergibt sich


{x : |x| > tn−1,1−α/2 }
K = {x : x > tn−1,1−α }


{x : x < −tn−1,1−α }
.
Beispiel. Zur Beurteilung der Qualität eines neuen Streckenmessgeräts wird eine 1 km lange
Referenzstrecke n = 10 mal gemessen. Das Messgerät liefert dabei für x1 , . . . , xn die folgenden
Werte (in Meter):
998,0;
1001,0;
1003,0;
1000,5;
999,0;
997,5;
1000,0;
999,5;
996,0;
998,5.
Wir nehmen die Zufallsgröße „gemessene Länge“ als normalverteilt an. Aus den Messwerten
erhalten wir
X̄n = 999,3 m,
s2n = 3,9 m2 ,
sn = 1,975 m.
Uns interessiert nun, ob das Gerät im Mittel die korrekte Entfernung liefert, d.h. wir testen die
69
Hypothese H0 : µ = µ0 = 1000 m. Die Alternativhypothese ist H1 : µ ̸= µ0 . Die Irrtumswahrscheinlichkeit sei α = 0,05 und als kritischen Bereich haben wir
K = {x : |x| > t9;0,975 = 2,262} = (−∞; −2,262) ∪ (2,262; ∞).
Die Testfunktion liefert
Tn(6) (x1 , . . . , xn ) =
X̄n − µ0 √
999,3 − 1000 √
n=
10 = −1,12 ̸∈ K.
sn
1,975
Die Messwerte sprechen also nicht gegen unsere Behauptung. Wir können somit annehmen,
dass das Messgerät im Mittel korrekt arbeitet.
2.5.3.3 Hypothesen über σ 2 bei unbekanntem µ
Sei µ unbekannt und durch X̄n geschätzt und der Wert σ02 vorgegeben. Wir testen drei verschiedene Nullhypothesen H0 mit der jeweiligen Alternativhypothese H1 :


2
2
2
2


σ ̸= σ0
σ = σ 0
und
H1 : σ 2 > σ02 .
H0 : σ 2 ≤ σ02


 2
 2
σ < σ02
σ ≥ σ02
Als Testfunktion wählen wir
Tn(5) (X1 , . . . , Xn ) =
n
1 ∑
(n − 1)Sn2
2
(X
−
X̄
)
=
∼ χ2n−1 .
i
n
σ2
σ2
i=1
Als kritischer Bereich ergibt sich

2
2

{x : x < χn−1,α/2 ∨ x > χn−1,1−α/2 }
K = {x : x > χ2n−1,1−α }


{x : x < χn−1,α }
.
Beispiel. Wir betrachten nochmals das vorhergehende Beispiel des Streckenmessgeräts. Wir
möchten nun weitere Aussagen über die Qualität des Geräts machen, indem wir die Hypothese
H0 : σ 2 ≥ σ02 = 4 m testen. Dann ist H1 : σ 2 < σ02 und mit α = 0,05 und
K = {x : x < χ29;0,05 = 3,325} = (0; 3,325)
liefert die Testfunktion
Tn(5) (x1 , . . . , xn ) =
(n − 1)Sn2
9 · 3,9
=
= 8,775 ̸∈ K,
σ2
4
d.h. die Messwerte sprechen nicht gegen die Hypothese. Aus praktischer Sicht ist die hohe
Varianz ein Merkmal für schlechte Messqualität.
70
2.5.4 Vergleich zweier normalverteilter Grundgesamtheiten
Wir betrachten die zwei normalverteilten Grundgesamtheiten X (1) ∼ N(µ1 , σ12 ) und X (2) ∼
(1)
(1)
(2)
(2)
N(µ2 , σ22 ). Die zufälligen Vektoren (X1 , . . . , Xn1 ) und (X1 , . . . , Xn2 ) seien entsprechende Stichproben. Wir gehen davon aus, dass σ12 = σ22 gilt und möchten wissen, ob die Erwartungswerte der beiden Grundgesamtheiten übereinstimmen, d.h. wir testen die Hypothese
H0 : µ1 = µ2 . Die Alternativhypothese ist H1 : µ1 ̸= µ2 und α sei die Irrtumswahrscheinlichkeit.
Wir verwenden als Testfunktion
√
X̄n1 − X̄n2
n1 · n2
(1)
(2)
(2)
√
)
=
,
.
.
.
,
X
,
X
Tn (X1 , . . . , Xn(1)
∼ tn1 +n2 −2
n2
1
1
2 +(n −1)S 2
(n2 −1)Sn
n
2
n2
1 + n2
1
n1 +n2 −2
und als kritischen Bereich
K = {x : |x| > tn1 +n2 −2,1−α/2 }.
Beispiel. Ein TV-Gerätehersteller bezieht Transistoren von zwei verschiedenen Lieferanten.
Die gelieferten Transistoren sollen einen Stromverstärkungsfaktor von 100 haben. Uns interessiert nun, ob die Mittelwerte µ1 und µ2 der Stromverstärkungsfaktoren bei beiden Lieferanten
übereinstimmen, wenn wir davon ausgehen, dass σ12 = σ22 gilt. Es sei α = 0,05 und die beiden
Stichproben liefern
n1 = 36, x̄n1 = 108,1, s2n1 = 13,6,
n2 = 28, x̄n2 = 99,8, s2n2 = 16,7.
Der kritische Bereich ist
K = {x : |x| > t62;0,975 = 1,999} = (−∞; -1,999) ∪ (1,999; ∞)
und aus der Testfunktion erhalten wir
Tn = 8,519 ∈ K.
Somit wird die Hypothese abgelehnt, d.h. die Erwartungswerte der Stromverstärkungsfaktoren
beider Lieferanten stimmen nicht überein.
Beim Test der Erwartungswerte der beiden Grundgesamtheiten auf Gleichheit haben wir die
Gleichheit der beiden Streuungen vorausgesetzt. Auch dies können wir als Hypothese verwenden, d.h. wir testen H0 : σ12 = σ22 mit der entsprechenden Alternativhypothese H1 : σ12 ̸= σ22 .
Als Testfunktion nutzen wir
(1)
(2)
Tn (X1 , . . . , Xn(1)
, X1 , . . . , Xn(2)
)=
1
2
Sn21
∼ Fn1 −1,n2 −1
Sn22
und als kritischen Bereich
K = {x : x < Fn1 −1,n2 −1,α/2 ∨ x > Fn1 −1,n2 −1,1−α/2 }.
Beispiel. Für das vorhergehende Beispiel erhalten wir beim Test auf Streuungsgleichheit mit
α = 0,1
K = {x : x < F35;27;0,05 ∨ x > F35;27;0,95 } = (0; 0,553) ∪ (1,857; ∞)
71
und
Tn = 0,814 ̸∈ K.
Wir können somit davon ausgehen, dass die Streuungen bei beiden Lieferanten gleich sind. Für
α = 0,05 erhält man K = (0; 0,493) ∪ (2,097; ∞).
2.5.5 χ2 -Test
Beim χ2 -Test (Chi-Quadrat-Test) handelt es sich um einen parameterfreien Test, d.h. wir testen
anhand einer Stichprobe (X1 , . . . , Xn ), ob die Verteilungsfunktion F einer Grundgesamtheit X
mit einer vorgegebenen Verteilungsfunktion F0 übereinstimmt. Das Testschema für Parametertests kann mit geringen Anpassungen auch für parameterfreie Tests verwendet werden. Als
Nullhypothese haben wir H0 : F (x) = F0 (x) mit der Alternativhypothese H1 : F (x) ̸= F0 (x).
Hauptproblem bei parameterfreien Tests ist das Finden einer geeigneten Testfunktion.
Vorgehensweise. Als ersten Schritt unterteilen wir die reellen Zahlen in r paarweise disjunkte
Intervalle I1 , . . . , Ir :
R = I1 ∪ · · · ∪ Ir = (−∞, a1 ) ∪ [a1 , a2 ) ∪ · · · ∪ [ar−2 , ar−1 ) ∪ [ar−1 , ∞).
Dann bestimmen
wir für jedes Intervall die Anzahl yi der Stichprobenelemente im Intervall Ii
∑
(es gilt ri=1 yi = n) und die „ideale“ Anzahl yi0 von Stichprobenelementen im Intervall Ii , d.h.
die der vorgegebenen Verteilung F0 entsprechende Anzahl. Unter der Annahme, dass H0 richtig
ist, gilt also yi0 = n · PH0 (X ∈ Ii ). Als Testfunktion verwenden wir
T =
r
∑
(yi − y 0 )2
i
i=1
yi0
∼ χ2r−1−m ,
wobei m die Anzahl der unbekannten und somit zu schätzenden Parameter der angenommenen
Verteilung ist. Bezeichnen wir mit α die Irrtumswahrscheinlichkeit, so erhalten wir als kritischen
Bereich
K = {x : x > χ2r−1−m,1−α }.
Bemerkung. Um den bei dieser Vorgehensweise gemachten Fehler gering zu halten, sollte die
Faustregel yi0 ≥ 5 beachtet werden.
Beispiel. Beim maschinellen Zuschnitt von Holzleisten wird anhand einer Stichprobe die Abweichung der tatsächlichen Länge vom Nennmaß untersucht. Wir vermuten, dass es sich bei
der Zufallsgröße „Betrag der Abweichung vom Nennmaß“ um eine normalverteilte Zufallsgröße
handelt. Die Nullhypothese ist also
)
(
X −µ
H0 : F (x) = Φ
σ
und wir haben m = 2 (die Parameter µ und σ 2 sind unbekannt und müssen geschätzt werden).
Aus der Stichprobe erhalten wir die folgenden Daten:
n = 150,
µ ≈ x̄n = 40,48,
72
σ ≈ sn = 5,71.
Wir wählen als Irrtumswahrscheinlichkeit α = 0,1 und zerlegen die reellen Zahlen in r = 8
Intervalle wie in der Tabelle angegeben:
i
1
2
3
4
5
6
7
8
Ii
0 – 30,5
30,5 – 33,5
33,5 – 36,5
36,5 – 39,5
39,5 – 42,5
42,5 – 45,5
45,5 – 48,5
48,5 – ∞
yi
5
13
23
22
29
29
16
13
yi0
6,03
10,59
19,81
28,35
30,94
25,81
16,44
12,01
Der kritische Bereich ist
K = {x : x > χ2r−1−m,1−α = χ25;0,9 = 9,27} = (9,27; ∞)
und die Testfunktion liefert
T =
8
∑
(yi − y 0 )2
i
i=1
yi0
= 3,27 ̸∈ K.
Wir können also davon ausgehen, dass die betragsmäßige Abweichung vom Nennwert normalverteilt ist.
2.6 Spezielle Schätzverfahren
2.6.1 Maximum-Likelihood-Methode
Im Folgenden sei X eine Grundgesamtheit mit der Verteilungsfunktion Fϑ und (X1 , . . . , Xn )
eine Stichprobe. Der Parameter ϑ ∈ Θ der Verteilung der Grundgesamtheit ist unbekannt
und soll geschätzt werden. Ziel der Maximum-Likelihood-Schätzung (kurz: MLS) ist es, den
Schätzwert ϑ̂M L für ϑ so zu wählen, dass die zur Schätzung verwendete Stichprobe unter allen
denkbaren Stichproben die höchste Wahrscheinlichkeit aufweist.
Dazu drückt man die Wahrscheinlichkeit der Stichprobe als Funktion von ϑ aus und sucht
das Maximum. Eine solche Funktion heißt Likelihood-Funktion und wird mit like(ϑ) bezeichnet.
Meist ist es einfacher, das Maximum der Funktion L(ϑ) := ln like(ϑ) zu bestimmen. Da die
Logarithmusfunktion streng monoton wachsend ist, ändert sie nichts an den Extremwerten. Die
Maximierung erfolgt wie üblich durch Nullsetzen der ersten Ableitung L′ (ϑ).
Eigenschaften der Maximum-Likelihood-Schätzung
• Alle MLS sind konsistent.
• Existiert eine wirksamste Schätzfunktion, so erhält man diese durch die MLS.
• MLS sind asymptotisch normalverteilt mit dem Erwartungswert ϑ.
73
2.6.1.1 Diskreter Fall
Sei (x1 , . . . , xn ) eine konkrete Stichprobe. Verwenden wir die Bezeichnung pxi (ϑ) = P (X = xi ),
so ist die Likelihood-Funktion gegeben durch
like(ϑ) = P (X1 = x1 , . . . , Xn = xn ) =
n
∏
pxi (ϑ).
i=1
Beispiel. Der Parameter ϑ = p ∈ (0, 1) einer binomialverteilten Grundgesamtheit X ∼ B(1, p)
ist zu bestimmen. In der dazu entnommenen Stichprobe (x1 , . . . , xn ) vom Umfang n tritt l mal
die 1 und n − l mal die 0 auf. Somit ist
like(p) = pl (1 − p)n−l
und
L(p) = ln(pl (1 − p)n−l ) = l ln p + (n − l) ln(1 − p).
Daraus erhalten wir
L′ (p) =
l
n−l
−
=0
p 1−p
⇔
l(1 − p) = p(n − l)
⇔
p=
l
= x̄n =: p̂M L .
n
Die Maximum-Likelihood-Methode liefert uns also als Schätzung die bereits bekannte erwartungstreue und konsistente Schätzfunktion X̄n .
2.6.1.2 Stetiger Fall
Sei (x1 , . . . , xn ) eine konkrete Stichprobe. Ist f = f (x, ϑ) die vom unbekannten Parameter
ϑ abhängige Dichtefunktion der stetig verteilten Grundgesamtheit X, so ist die LikelihoodFunktion
n
∏
like(ϑ) =
f (xi , ϑ)
i=1
und durch Logarithmieren erhalten wir
L(ϑ) = ln like(ϑ) =
n
∑
ln f (xi , ϑ).
i=1
Beispiel. Für eine normalverteilte Grundgesamtheit X ∼ N(µ, ϑ) ist anhand der Stichprobe
(x1 , . . . , xn ) der Parameter ϑ = (µ, σ 2 ) der Verteilung zu bestimmen. Es ist
)
(
n
1
1 ∑
2
2
like(µ, σ ) =
(xi − µ)
exp − 2
2σ
(2πσ 2 )n/2
i=1
und
n
n
1 ∑
2
L(µ, σ ) = − ln(2πσ ) − 2
(xi − µ)2 .
2
2σ
2
i=1
74
Daraus erhalten wir zum einen
n
∂L(µ, σ 2 )
1 ∑
= 2
(xi − µ) = 0
∂µ
σ
⇔
n
∑
−nµ +
i=1
1∑
xi = x̄i =: µ̂M L ,
n
n
xi = 0
⇔
µ=
i=1
i=1
d.h. die Maximum-Likelihood-Methode liefert für µ die bereits bekannte Schätzfunktion X̄n ,
und zum anderen (σ 2 ist hier als Symbol zu verstehen)
n
∂L(µ, σ 2 )
n
1 ∑
=− 2 + 4
(xi − µ)2 = 0
∂σ 2
2σ
2σ
i=1
⇔
n
n
1∑
1∑
2
2
2
(xi − µ) =
(xi − x̄n )2 =: σ̂M
σ =
L.
n
n
i=1
i=1
Diese Schätzung ist im Gegensatz zur schon bekannten Schätzfunktion Sn2 für die Varianz nicht
erwartungstreu.
2.6.2 Momentenmethode
Sei X eine Grundgesamtheit mit der Verteilungsfunktion Fϑ und (X1 , . . . , Xn ) eine Stichprobe.
Der unbekannte Parameter ϑ ist zu schätzen. Neben dem bereits bekannten k-ten Moment
mk = EX k der Zufallsgröße X führen wir noch das sogenannte k-te Stichprobenmoment
1∑ k
Xi
n
n
Mk =
i=1
ein. Die Schätzung nach der Momentenmethode besteht darin, die Momente von X mit den
Stichprobenmomenten gleichzusetzen. Besteht ϑ = (ϑ1 , ϑ2 ) zum Beispiel aus zwei einzelnen
Parametern, so löst man das Gleichungssystem m1 = M1 und m2 = M2 für eine konkrete
Stichprobe (x1 , . . . , xn ) und erhält daraus eine Schätzung ϑ̂M M für den gesuchten Parameter
ϑ. Bei Bedarf können auch die k-ten zentralen Momente µk = E(X − EX)k von X mit den
entsprechenden Schätzungen M̃k verwendet werden.
Beispiel. Sei X ∼ πλ eine mit dem Parameter ϑ = λ Poisson-verteilte Grundgesamtheit und
(x1 , . . . , xn ) eine Stichprobe. Dann ist
1∑
M1 =
xi .
n
n
m1 = EX = λ
und
i=1
Setzen wir m1 = M1 , so erhalten wir die Schätzung
1∑
xi .
n
n
λ̂M M =
i=1
Beispiel. Sei X eine auf dem Intervall [a, b] gleichverteilte Grundgesamtheit und (x1 , . . . , xn )
eine Stichprobe. Wir möchten aus dieser Stichprobe die Parameter a und b bestimmen. Dazu
75
verwenden wir
m1 = EX =
a+b
,
2
1∑
xi = x̄n ,
n
n
M1 =
µ2 = D2 X =
i=1
(b − a)2
,
12
M̃2 = s2n .
Aus dem Gleichungssystem m1 = M1 und µ2 = M̃2 ergeben sich die Schätzungen
√
√
âM M = x̄n − 3sn
und
b̂M M = x̄n + 3sn .
2.6.3 Methode der kleinsten Quadrate
Gegeben sei eine Funktion ϕ = ϕ(t, β) (z.B. Temperatur einer Flüssigkeit) mit einem frei
wählbaren Parameter t (z.B. Zeit) und einem unbekannten Parameter β = (β1 , . . . , βr ). Der Typ
der Funktion (z.B. linear) sei bekannt. Um β zu bestimmen werden für n verschiedene Werte
t1 , . . . , tn von t durch Messung die entsprechenden Funktionswerte yi bestimmt, wobei n ≫ r ist.
Bei den Messungen treten Messfehler auf, d.h. es gibt bei jeder Messung eine Abweichung ηi =
ϕ(ti , β) − yi zwischen Funktionswert und Messwert. Dabei gilt η = (η1 , . . . , ηn ) ∼ N(0, Covη).
Sinn und Zweck der Methode der kleinsten Quadrate ist es nun, den Parameter β der Funktion
ϕ so zu wählen, dass die Summe der Quadrate der Abweichungen ηi möglichst klein ist. Es soll
also eine Schätzung β̂ M KQ für β gefunden werden, für die
n
∑
(ϕ(ti , β) − yi )2
i=1
minimal wird.
76