1.4. Wahrscheinlichkeitsverteilung von Zufallsgrößen

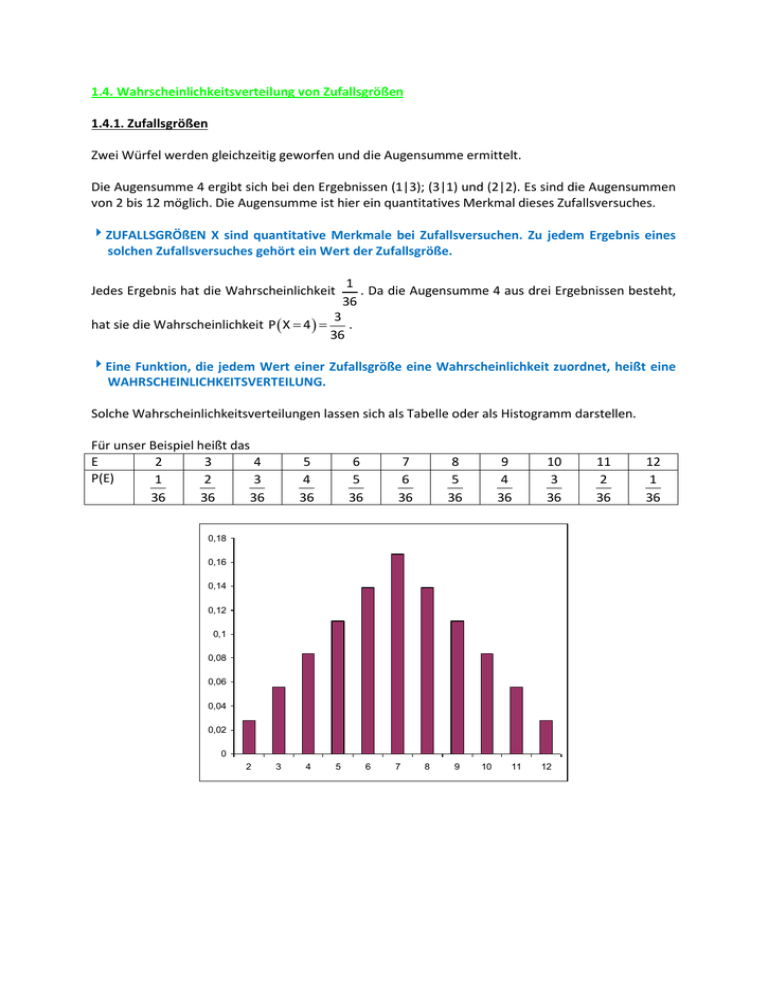
1.4. Wahrscheinlichkeitsverteilung von Zufallsgrößen
1.4.1. Zufallsgrößen
Zwei Würfel werden gleichzeitig geworfen und die Augensumme ermittelt.
Die Augensumme 4 ergibt sich bei den Ergebnissen (1|3); (3|1) und (2|2). Es sind die Augensummen
von 2 bis 12 möglich. Die Augensumme ist hier ein quantitatives Merkmal dieses Zufallsversuches.
ZUFALLSGRÖßEN X sind quantitative Merkmale bei Zufallsversuchen. Zu jedem Ergebnis eines
solchen Zufallsversuches gehört ein Wert der Zufallsgröße.
1
. Da die Augensumme 4 aus drei Ergebnissen besteht,
36
Jedes Ergebnis hat die Wahrscheinlichkeit
hat sie die Wahrscheinlichkeit P  X  4  
3
.
36
Eine Funktion, die jedem Wert einer Zufallsgröße eine Wahrscheinlichkeit zuordnet, heißt eine
WAHRSCHEINLICHKEITSVERTEILUNG.
Solche Wahrscheinlichkeitsverteilungen lassen sich als Tabelle oder als Histogramm darstellen.
Für unser Beispiel heißt das
E
2
3
4
P(E)
1
2
3
36
36
36
5
4
36
6
5
36
7
6
36
8
5
36
9
4
36
10
3
36
0,18
0,16
0,14
0,12
0,1
0,08
0,06
0,04
0,02
0
2
3
4
5
6
7
8
9
10
11
12
11
2
36
12
1
36