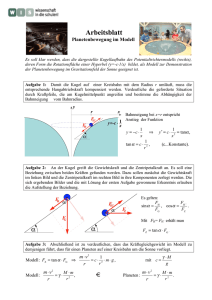
Mechanik 1. Kräfte und geradlinige Bewegungen

Mechanik
Buch: Dorn-Bader PHYSIK 11
1. Kräfte und geradlinige Bewegungen
i
1.1. Trägheitsgesetz
Dorn-Bader S. 6/7
Versuch: Schüler beschleunigen und verzögern einen PKW
Sieht man von den Reibungskräften ab, dann lässt sich der PKW ohne große Anstrengung auf der horizontalen Straße verschieben.
Schieben die Schüler mit großer Kraft, dann beschleunigen sie das Auto. Überlassen
sie nach einiger Zeit das Fahrzeug sich selbst, so würde es - könnte man den Einfluss der Reibung ausschließen - immer gleich schnell geradeaus weiterfahren. Soll
das Auto wieder in den Stillstand gebracht werden, dann müssen die Schüler wieder mit großer Kraft gegen die Fahrtrichtung ziehen. Das Auto widersetzt sich jeder
Veränderung der Geschwindigkeit, es ist träge.
vgl. Abbildung B3 und B4, Dorn-Bader S. 6/7
Die Kraft, die zum Beschleunigen oder
Verzögern eines Körpers nötig ist, kann
viel größer als dessen Gewichtskraft sein.
Wenn man mit der Stativstange ruckartig
Kraftmesser
Faden
10 N
das Massestück nach unten zieht, reißt der
untere Faden, da die Kraft, um das Massestück so stark zu beschleunigen, viel gröFaden
ßer als die Zugfestigkeit des Fadens ist.
Massestück
Massestück
Der Kraftmesser wird kaum zusätzlich be0,5 kg
0,5 kg
lastet. Zieht man langsam am Faden, dann
reißt der obere Faden, da an ihm dann
Faden
Faden
die Zugkraft und die Gewichtskraft ankurze Stativstange kurze Stativstange
greifen. Am unteren Faden greift nur die
Gewichtskraft an.
Die Trägheit eines Körpers tritt auch im schwerelosen Weltraum auf. Auch dort brauchen Raumschiffe zum Schnellerwerden, Abbremsen oder zur Richtungsänderung
die Kraft ihrer Raketentriebwerke. Ohne Raketenmotor würde sich ein Raumschiff,

das weitab von Himmelskörpern ist, mit immer gleicher Geschwindigkeit geradeaus
fliegen.
Ohne äßere Kraft ändert ein Körper seinen Bewegungszustand nicht, d. h. er bleibt
in Ruhe oder er behält seine Bewegung mit konstanter Geschwindigkeit in immer
gleicher Richtung bei. Die Richtungsänderung beim Autofahren ist nur durch die
Haftkraft zwischen den Reifen und der Straße möglich. Bei Glatteis fehlt diese äßere
Kraft weitgehend! Dann beharrt das Auto wegen seiner Trägheit auf Geradeausfahrt.
Weitere Beispiele zur Trägheit
• Die Endolymphe in den Bogengängen des Innenohrs reagiert auf Beschleunigungen und reizt dabei Sinneszellen. vgl. Abbildung B6 Dorn-Bader i S. 7
• Gitarrenspiel, Hammerschläge, ...
Aufgabe: Nenne weitere Beispiele, in denen Trägheit eine Rolle spielt.
Körper, auf die keine äßere Kraft wirkt, verharren in ihrem Bewegungszustand:
Körper sind träge.
Werden sie schneller oder langsamer oder ändern sie ihre Bewegungsrichtung, so
müssen äßere Kräfte wirken.
1.2. Gleichgewicht der Kräfte
Dorn-Bader S. 8 Bild B1
Greift an einem ruhenden Körper nur eine Kraft an, so setzt er sich in Bewegung.
Wirken auf ein und denselben Körper zwei entgegengesetzt gerichtete, gleich große
Kräfte, dann bleibt er in Ruhe, es herrscht Kräftegleichgewicht. Die resultierende
Kraft ist null.
Damit der Körper kein Drehmoment erF2
F1
fährt, müssen die Kräfte in derselben WirWirkungslinie
kungslinie angreifen.
Ist die Resultierende aller an einem Körper angreifenden Kräfte
gleich null, so herrscht am Körper Kräftegleichgewicht. Ist der Körper in Ruhe, so bleibt er in Ruhe. Er kann höchstens verformt oder
gedreht werden.
Ist ein Körper in Bewegung, so bleibt er nur dann gleich schnell in
geradliniger Bewegung, wenn an ihm Kräftegleichgewicht besteht.
Ist die resultierende Kraft an einem Körper ungleich null, so wird
sein Bewegungszustand geändert.

1.3. Kraftmessung - Kraftvektoren
Für Kraftmessungen werden meistens Federkraftmesser verwendet, die in der Krafteinheit 1 Newton geeicht sind. (vgl. Dorn-Bader Abb. B 1) Bei den in Kraftmessern
verwendeten Stahlfedern ist die Kraft F und die Verlängerung s innerhalb eines gewissen Bereichs einander proportional (F ∼ s). Die Kraft F und die Auslenkung s
erfüllen das hookesche Gesetz F = D · s. Man nennt D Federkonstante. Ihre Einheit
N
.
ist [ D ] = 1 m
Gewichtskraft:
Körpern schreibt man als Maß für das Schwersein eine Masse zu. Zwei Körper haben
dieselbe Masse, wenn sie am gleichen Ort die gleiche Gewichtskraft erfahren. Es gilt
der wichtige Zusammenhang zwischen Gewichtskraft G und Masse m: G = m · g mit
N
g als Ortsfaktor. Für Mitteleuropa beträgt er etwa 9,81 kg
.
1.4. Addition und Zerlegung von Kräften
Darstellung: Kraftpfeil
F
A
Angriffspunkt
Die Länge des Kraftpfeils entspricht der Größe
oder dem Betrag der Kraft (z. B. 5 N).
Bei Kräften spielt der Angriffspunkt und die
Richtung eine wichtige Rolle.
Die Variablennamen von Kräften werden häufig mit einem darübergesetzten Pfeilzeichen
(→) gekennzeichnet. Im Folgenden wird aber
dennoch meistens auf diese Kennzeichnung
verzichtet.
Versuch: Resultierende Kraft

A
90◦
A kann sowohl allein durch
die resultierende Kraft ~F als
auch durch die Komponenten
F1 und F2 in die gleiche Position gebracht.
Aufgabe
Konstruiere das Kräfteparallelogramm (1 cm =
b 0,5 N)!
~2
F
~1
F
~F
250 g
500 g
Hinweis: vgl. Dorn-Bader Abb. B3 S. 11
Liegen die Kräfte auf einer Geraden, dann kann man mit den Größen der Kräfte wie
mit reellen Zahlen rechnen. Man vereinbart z. B.: Kräfte nach rechts erhalten positive,
solche nach links negative Werte.
Merke:
Die resultierende Kraft F zweier Kräfte F1 und F2 ergibt sich aus der
Diagonalen des Kräfteparallelogramms mit den Seiten F1 und F2 .
Umgekehrt kann auch eine gegebene Kraft F in zwei Komponenten
F1 und F2 zerlegt werden. Die Richtungen der Komponenten werden
nach physikalischen Gesichtspunkten gewählt.
Versuch: Zerlegung in Komponenten Abb. B3: Straßenlaterne
Aufgabe A3 S. 12
Merke:
Bei der Untersuchung der Kräfte muss man zwischen Kräftedreieck und Längendreieck unterscheiden. Meistens lassen sich Winkelgrößen aus dem Längendreieck
ermitteln, welches ähnlich zum Kräftedreieck ist.
Kraftkomponenten an der schiefen Ebene Dorn-Bader S. 12 Bild B2
Welche Kraft beschleunigt ein Fahrrad bei der Talfahrt?

FH
Hangabtriebskraft:
Normalkraft:
α
FN
α
G
Aufgaben: Buch S. 12 A1, A2, A4
Schülerarbeit: vgl. Dorn-Bader S. 13
Informiere dich über moderne Messmethoden zur Kräftemessung.

FH = G · sin α
FN = G · cos α
2. Kinematik (Wiederholung)
2.1. Gleichförmige Bewegung
Bei einer gleichförmigen Bewegung werden in gleichen Zeitabschnitten ∆t stets die
gleichen Strecken ∆s zurückgelegt.
s
s
s
Abb. 1
Abb. 2
Abb. 3
∆s
∆s
∆t
s
∆s
∆t
∆t
t
t
s
∆s
v= =
t
∆t
t
v=
t
∆s
∆t
v=
∆s
∆t
A BB .1
Das Zeit-Weg-Diagramm ist eine Gerade. Die Geschwindigkeit v einer gleichförmi∆s
. Sie ist kongen (geradlinigen) Bewegung ergibt sich aus dem Quotienten v =
∆t
stant. Misst man den Weg s und die Zeit t von einem gemeinsamen Nullpunkt aus,
s
so gilt bei der gleichförmigen Bewegung zudem v = .
t
v
v
Abb. 1
v
Abb. 2
t
t
Abb. 3
t
A BB .2
m
s
Bei einer gleichförmigen Bewegung ist die Geschwindigkeit konstant. Das Zeit-GeschwindigkeitsDiagramm ist somit eine horizontale Gerade.
Einheit der Geschwindigkeit: [v] = 1
Beispiel Dorn-Bader S. 19

Hinweis:
• Betrachtet man die Fläche unter der horizontalen v-Geraden im t-v-Diagramm
(vgl. Dorn-Bader Abb. B1 und Abb. B3 S. 18), so erkennt man, dass der Flächeninhalt des zugehörigen Rechtecks den in der Zeit t zurückgelegten Weg angibt.
• Bei einer Bewegung gegen die festgelegte positive Richtung liegen die v-Kurve
und die Fläche im negativen Bereich.
Übungen Dorn-Bader S. 19 Nr. A1, A2, A3, A4
2.2. Beschleunigte Bewegung
Nimmt die Geschwindigkeit in einer Bewegung mit der Zeit t zu, dann ist die Bewegung beschleunigt. Nimmt die Geschwindigkeit in einer Bewegung mit der Zeit t ab,
dann ist die Bewegung verzögert.
v
v
v
1
2
∆v
2
1
v
∆t
2
3
∆v v
4
∆t
t
t
t
t
∆t
3
∆v
t
A BB .3
(1)
(3)
gleichmäßig beschleunigte Bewegung
gleichmäßig verzögerte Bewegung
(2)
(4)
gleichförmige Bewegung
ungleichmäßig beschleunigte Bewegung
Aufgaben
• Wie lassen sich die zurückgelegten Wege bestimmen?
• Zeichne mögliche t-s-Diagramme dazu.
Merke:
Es gilt allgemein:
Im t-v Schaubild wird der zurückgelegte Weg s stets durch den Flächeninhalt unter
der t-v-Kurve angegeben.
Begründung: Dorn-Bader S. 20 (Vertiefung)
Die Fläche lässt sich aus schmalen Rechtecken mit der Grundseite ∆t und der Höhe v
zusammensetzen.

2.3. Momentangeschwindigkeit
Die Geschwindigkeit ist definiert als v =
tervall ∆t.
∆s
, d. h. als die Wegänderung ∆s im Zeitin∆t
Wie kann aber die Geschwindigkeit in einem Zeitpunkt angegeben werden?
Gleichförmige Bewegung vgl. Abb. ?? und Abb. ??
Hier kann jedes Zeitintervall zur Bestimmung der Geschwindigkeit v gewählt wer∆s
den, da
unabhängig von der Größe des betrachteten Zeitintervalls ∆t ist.
∆t
Beschleunigte Bewegung
v
s
P (t)
∆s
∆s
∆t
∆t
t
t
Wächst die Geschwindigkeit mit t, dann ist das t-s-Diagramm keine Gerade mehr
∆s
ändert sich in Abhängigkeit von ∆t und von t. Um die Geschwindigkeit in
und
∆t
∆s
einem Zeitpunkt zu ermitteln, muss
für sehr kleine Zeitintervalle ∆t bestimmt
∆t
werden. Damit entspricht die Geschwindigkeit im Zeitpunkt t der Steigung der Tangente im Punkt P(t) des t-s-Schaubildes.
Nimmt die Geschwindigkeit v einer Bewegung gleichmäßig mit der Zeit t zu, d. h.
v ∼ t, dann gilt für das t-v-Gesetz v = a · t, falls die Bewegung aus dem Stand
beschleunigt wird.
Für das entsprechende Geschwindigkeits-Zeit-Diagramm ergibt sich eine Ursprungsgerade. Man erkennt, dass in gleichen Zeitabschnitten ∆t die Geschwindigkeitszu∆v
v
heißt Beschleunigung.
nahme ∆v ebenfalls gleichbleibt. a = =
t
∆t

m
.
s2
Bewegungen mit konstanter Beschleunigung nennt man gleichmäßig beschleunigt.
m
Die vom Anfahrpunkt (t = 0 s;v = 0 ) aus gemessene Wegstrecke lässt sich aus
s
dem t − v-Schaubild ermitteln.
1
Es ergibt sich das Zeit-Weg-Gesetz: s = a · t2
2
Einheit: [ a] = 1
Gleichförmige Bewegung
v = konstant;
Gleichmäßig
beschleunigte Bewegung
Sonderfall:
s = v·t
a = konstant
v = a·t
s=
1 2
at
2
Dorn-Bader S. 46/47
Freier Fall
v = g·t
s=
1 2
gt
2
Übungen Dorn-Bader
S. 23 Nr. A2, A3
S. 27 Nr. A2 - A6
S. 47 Nr. A1, A2, A3, A5

mit
g = 9,81
m
s2
3. Newtonsches Grundgesetz
Dorn-Bader: Physik 11, S. 30 ff
Die nötige Kraft beim Anfahren eines Fahrzeugs hängt von der gewünschten Beschleunigung, aber auch vom Fahrzeug und seiner Beladung ab.
Diese Abhängigkeiten sollen getrennt untersucht werden.
Wie hängt die nötige Kraft F bei ein und demselben Fahrzeug von der gewünschten Beschleunigung ab?
Versuch
Zur Beschleunigung werden Massestücke von m B =10 g, m B =20 g und m B =30 g
eingesetzt. Die beschleunigende Kraft F ergibt sich aus der Gewichtskraft der Massestücke. F = G = m B · g
Damit stets dieselbe Gesamtmasse beschleunigt wird, belädt man den Luftkissengleiter der Masse mw jeweils mit den restlichen Wägestücken. Die gesamte beschleunigte
Masse m ergibt sich somit durch m = mw + m B = 230 g und bleibt konstant. Mit
einem Bewegungsaufnehmer wird über den Computer (CASSY) direkt der Weg s in
Abhängigkeit von der Zeit t aufgenommen. Das Programm kann aus diesen Daten
∆s
∆v
auch gleich die Geschwindigkeit v =
und die Beschleunigung a =
ermitteln.
∆t
∆t

Versuchshinweise zum CASSY von Leybold:
• Beispiel m = konstant laden
• Gegebenenfalls das Vorzeichen der Wegmessung invertieren (s = −s)
• Wegnullpunkt definieren (→ 0 ← in Einstellungen sA1)
• Messung mit F9 starten und am Ende wieder mit F9 stoppen.
• Bei der ersten Messung ist darauf achten, dass alte Messungen gelöscht werden.
Anschließend sollen die weiteren Messungen hinzugefügt werden.
• Neben dem s-t-Diagramm sind auch die v-t und a-t-Diagramme vorhanden.
Ergebnis:
Die Beschleunigung a, die ein bestimmter Körper erfährt, ist der an ihm angreifenden
Kraft F proportional: F ∼ a .
Wie hängt die Kraft F vom Fahrzeug und seiner Beladung ab, wenn sich die Beschleunigung nicht ändern soll?
Versuchshinweise
• Es wird das gleiche CASSY-Programm verwendet.
•
1. Beschleunigung eines leeren Wagens (mw = 100 g) mit m B =10 g, d. h. F =
0,098 N.
m
m = 110 g =⇒ a = 0,86 2
s
2. Beschleunigung eines mit einer Scheibe (m = 100 g) beschwerten, d.h. doppelt so schweren Wagens durch 20 g, d. h. F = 0,196 N.
m = 220 g =⇒ a = 0,86
m
s2
Ergebnis:
Die Kraft F, die man zu einer bestimmten Beschleunigung braucht, ist der Masse m
des zu beschleunigenden Körpers proportional: F ∼ m .
Aus den obigen Messergebnissen folgt: F ∼ m · a =⇒ F = k · m · a.
k lässt sich aus einem Messbeispiel ermitteln:
m = 0,23 kg
F = 0,2 N
a = 0,83
m
kgm
=⇒ m · a ≈ 0,2 2 =⇒ k = 1
2
s
s
Diese Übereinstimmung ist kein Zufall. Die Kraft von 1 N hat man bereits als jene
verKraft definiert, welche einer Masse von m =1 kg eine Beschleunigung a = 1 m
s2
m
m
leiht, d. h. in 1 s von v = 0 auf v = 1 s beschleunigt.
s

t So wie die Krafteinheit 1 N werden in der Mechanik alle Einheiten auf die drei Basiseinheiten 1 m, 1 kg und 1 s zurückgeführt.
Merke: Grundgleichung der Mechanik:
F = m·a
Hinweis: Die beschleunigende Kraft im Newtonschen Grundgesetz ist die Resultierende der von außen einwirkenden Kräfte.
Beispiele: Dorn-Bader S. 33, Musteraufgaben a, b
Aufgaben: Dorn-Bader S. 33 Nr. A2 - A6
4. Kraft und Gegenkraft - Actio und Reactio
Dorn-Bader S. 34
Versuch
Seil
A
FB auf A
B
FA auf B
Zwei Personen (P1 , P2 ) nehmen
auf zwei Wagen Platz und ziehen sich mit einem Seil gleichmäßig gegenseitig an. Die Kraft, welche jeweils an einer Person angreift, wird durch einen Kraftmesser (20 N) angezeigt.
Ergebnis:
Die dazwischengeschalteten Kraftmesser zeigen immer die gleich großen Kräfte an.
Merke:
Greift der Körper A mit der Kraft F~A am Körper B an, so übt B auf A die Gegenkraft (reactio) F~B aus. Sie hat den gleichen Betrag wie F~A , aber die entgegengesetzte
Richtung: F~A = − F~B
Kraft und Gegenkraft (actio und reactio) greifen an verschiedenen Körpern an.
Übungen Dorn-Bader S. 35 A1, A2
Anwendungsbeispiele
Dorn-Bader S. 35
• Zu Lande
• In der Luft
• Im Wasser
• Im Weltraum

5. Reibung
Dorn-Bader S. 36 ff
Vollbremsung mit dem Auto
Das Auto übt auf die Straße eine Kraft nach vorne aus. Die Reactio der Straße wirkt
als Reibungskraft FR der Bewegung des Autos entgegen.
Bei sanftem Abbremsen, tritt Gleitreibung zwischen den Bremsbacken und der Felge
auf. Die Gleitreibungskraft ist umso größer, je stärker die Bremsbacken gegen die
Felge gedrückt werden.
Versuch Dorn-Bader S. 36 V1
• Wird die Normalkraft FN vergrößert, dann vergrößert sich proportional zur FN
die Gleitreibungskraft Fgl :
Merke:
Fgl ∼ FN
Fgl = f gl FN
( f gl ist die Gleitreibungszahl)
• Bei gleicher Normalkraft hängt die Gleitreibungskraft kaum von der Größe der
reibenden Flächen ab, wohl aber von deren Beschaffenheit.
Versuch Dorn-Bader Abbildung B2
Wir ziehen vorsichtig mit einem Kraftmesser an einem Klotz. Der Klotz bewegt sich
nicht. Die an ihm - und damit am Tisch - angreifende Kraft wird größer, aber entsprechend wächst die Reactio des Tisches, die den Klotz zurückhält. Dies ist die Haftkraft.
Sie erreicht irgendwann ihren größten Wert: maximale Haftkraft Fh,max . Ziehen wir
noch etwas stärker, so beginnt der Klotz zu gleiten. Die Reibungskraft geht wieder
auf die Gleitreibungskraft Fgl zurück.

vF
R
Fh,max
Fgl
t
Für die Haftkraft Fh gelten die gleichen Gesetzmäßigkeiten wie für die Gleitreibungskraft
Merke:
Fh ∼ FN
Fh = f h FN
( f h ist die Haftszahl)
Beispiele für f h und f gl : Dorn-Bader S. 37 Tabelle T1
Hinweis:
• Mikroskopische Erklärung:
Auch glattpolierte Oberflächen zeigen - mikroskopisch betrachtet - Unebenheiten. Die reibenden Körper berühren sich nur an diesen mikroskopisch kleinen
Unebenheiten. An diesen Mikrokontaktflächen sind die Moleküle der beiden
Körper so nahe beieinander, dass manche „Höcker“ miteinander verschweißen (Adhäsion). Reiben zwei Körper aneinander, dann müssen solche winzigen Verschweißungen aufgebrochen werden. Bei größerer Normalkraft werden
die Höckeroberflächen stärker verformt. Die Größe der Kontaktflächen wächst
dabei proportional zur Normalkraft.
• Haft- und Gleitreibungskräfte können durch Schmieren und Ölen deutlich verringert werden. Die für trockene Berührflächen gefundenen Gesetze gelten dann
aber nicht mehr.
• Die Rollreibungskraft ist wesentlich kleiner als Haft- oder Gleitreibungskraft.
Übungen
Dorn-Bader S. 37 A1 - A5

6. Verkehrsphysik 1
vgl. Dorn-Bader S. 38 ff
6.1. Kräfte beim Bremsen
Zum Abbremsen aus einer (positiven) Geschwindigkeit werden (negative) Kräfte benötigt. Wie groß sie sein müssen, hängt von der Masse des abzubremsenden Körpers und der gewünschten negativen Beschleunigung (Verzögerung) ab. Wird z. B.
ein Körper der Masse m = 70 kg mit der negativen Beschleunigung a = 6,4 m/s2 abgebremst, dann wirkt auf ihn eine Kraft von F = m · a = 70 kg · (6,4 m/s2 ) = 448 N
gegen die Bewegungsrichtung.
6.2. Brems- und Anhalteweg
Fahrzeug A soll mit der Geschwindigkeit v A = 36 km/h und das Fahrzeug B doppelt
schnell mit der Geschwindigkeit v B = 72 km/h fahren. Beide Fahrzeuge müssen
plötzlich eine Vollbremsung durchführen.
Vergleiche die Bremswege, wenn folgende Bedingungen gelten:
Haftzahl f h = 0,65, damit erhält man eine Verzögerung von a = 6,4 m/s2 .
Der Bremsvorgang setzt nach einer „Schrecksekunde“ ein.
6.3. Bedeutung des ABS
ABS sorgt durch Sensoren dafür, dass beim Bremsen stets die optimale Haftkraft zwischen Rad und Straße wirkt. Diese ist immer größer als die dortige Gleitreibungskraft
bei blockierten Rädern.
Achtung:
Auch die Haftkraft ist von der Straßenbeschaffenheit abhängig; d. h. bei Glatteis wächst
der Bremsweg um ein Vielfaches!
Vorteil des ABS:
Das Nichtblockieren erhält die Lenkfähigkeit der Vorderräder. Das Fahrzeug gerät
nicht so schnell ins Schleudern.
Übungen Dorn-Bader S. 39 Nr. A1 - A7

6.4. Crash
Dorn-Bader S. 40
Zeige, dass für die Bremsverzögerung a bei einer Geschwindigkeit v und einem Bremsv2
weg s gilt: a = .
2s
Fährt man mit 50 km/h gegen einen Baum, dann fliegen die nicht angeschnallten Insassen ungebremst gegen das Armaturenbrett solange das Auto zerknautscht. Dort erst
beginnt der Bremsvorgang. Es bleibt nur noch eine kurze Bremsstrecke (z. B. 5 cm).
Daraus resultieren eine Bremsverzögerung von a = 2000 m/s2 und bei einer Körpermasse von 70 kg eine Bremskraft der Größe 1,4 · 105 N. Diese Kraft ist i.A. tödlich.
Knautschzone und Sicherheitsgurt
Der Vorderteil des Autos wird - als Knautschzone - zusammengedrückt (z. B. 60 cm).
Der Gurt dehnt sich zusätzlich um eine bestimmte Strecke (z. B. 20 cm). Damit ergibt
sich ein größerer Bremsweg: s ≈ 0,8 m. Die Bremsverzögerung errechnet sich dann zu
v2
a=
= 120 m/s2 . Der Brustkorb muss dann eine verzögernde Kraft von F = ma =
2s
70 kg · 120 m/s2 = 8400 N aushalten. Dies ist mehr als die 12-fache Gewichtskraft.
Schutzwirkung eines Sturzhelmes
Ein Sturzhelm schützt nicht nur vor spitzen Gegenständen und Abschärfungen. Er
verteilt vor allem die einwirkende Kraft F auf eine größere Fläche A. Damit wird der
F
kleiner. Bei einem Sturz vergrößert er außerdem den Bremsweg von
Druck p =
A
ein bis zwei Millimetern auf einige Zentimeter.
Übungen Dorn-Bader S. 44 Nr. A1 - A13
7. Vektoraddition bei Bewegungen
Versuch
Ein Spielzeugauto fährt in Fahrtrichtung oder gegen die Fahrtrichtung einer Rolltreppe oder „überquert“ eine Rolltreppe (simuliert durch eine Tapete, die über den Tisch
gezogen wird).
Die Bewegung des Spiezeugautos wird vom außenstehenden Beobachter und vom
Fahrer im Auto unterschiedlich gesehen. Bewegungen werden relativ zum gewählten
Bezugssystem beschrieben.

∆s
s Es liegt nahe, ganz allgemein Geschwindigkeiten wie Kräfte als Vektoren aufzufassen. Man kann aus Geschwindigkeitskomponenten eine Resultierende Geschwindigkeit bilden.
v~1
v~1
~v
v~2
~v
v~2
Beispiele
km
eine Strecke
h
km
s = 1200 km von West nach Ost und zurück. Es herrscht Ostwind mit −60
.
h
Wie lange dauert der Flug?
a) Ein Flugzeug fliegt mit der Eigengeschwindigkeit von v1 = 540
Würde bei Windstille der Flug gleich lange dauern?
b) Du willst mit einem Kahn ans andere Ufer eines Flusses der Breite AB = 36 m.
Die Strömungsgeschwindigkeit des Wassers relativ zum Ufer hat den Betrag v0 =
m
m
3 . Der Kahn hat senkrecht zum Ufer eine Geschwindigkeit vk = 4 .
s
s
Welche resultierende Geschwindigkeit hat der Kahn relativ zum Ufer?
Welche Fahrstrecke relativ zum Ufer wird zurückgelegt?
Nach welcher Zeit erreichst du das gegenüberliegende Ufer?
Wie lange bräuchtest du, wenn du auf dem kürzesten Weg über den Fluss gelangen möchtest?
8. Waagerechter Wurf
Dorn-Bader S. 58 ff
Versuch

(t)
Abschussrichtung
re
age
Wa
Freier Fall
x
e
cht
urf
rW
y
Während die rechte Kugel horizontal abgeschossen wird, fällt
die linke Kugel gleichzeitig frei
nach unten.
Ergebnis
Die beiden Kugeln schlagen
gleichzeitig auf dem Boden auf.
Dabei spielt es keine Rolle, wie
hoch über dem Boden, die Kugelbewegungen beginnen. In
einer Stroboskopaufnahme (vgl.
Dorn-Bader S. 58) kann deutlich
erkannt werden, dass die Kugeln
ständig in gleicher Höhe sind;
d. h. auch die waagerecht abgeschossene Kugel fällt ständig
nach dem Gesetz des freien Falls.
Die Bewegung beim waagerechten Wurf kann als Überlagerung einer gleichförmigen
Bewegung in horizontaler Richtung und einer gleichförmig beschleunigten Fallbewegung in vertikaler Richtung gedeutet werden.
Ein außenstehender Beobachter beschreibt Ort und Geschwindigkeit mit den folgenden Gleichungen, wenn er den Koordinatenursprung in den Startpunkt, die x-Achse
in Richtung der waagerecht abgeschossenen Kugel und die y-Achse nach unten in
Richtung der frei fallenden Kugel legt.
Bahnkoordinaten: x = v0 · t
1
y = gt2
2
Geschwindigkeitskomponenten: v x = v0
vy = g · t
In jedem Punkt der Bahnkurve gilt für den Winkel ϕ des Geschwindigkeitsvektors
vy
g·t
=
. Die momentane (resultierende) Ge~v gegen die Horizontale: tan ϕ =
v x q v0
schwindigkeit errechnet sich nach v =
v2x + v2y . Aus der Koordinatendarstellung
der Wurfbahn kann durch Elimination der Zeitvariablen t die Gleichung der sogeg
x
=⇒ y = 2 · x2
nannten Wurfparabel bestimmt werden: t =
v0
2v0
Übungen
Dorn-Bader S. 63 A1, A2

9. Energieerhaltung
9.1. Energieformen
Elektrische Energie, chemische Energie (Benzin, Kohle), Kernenergie, Sonnenenergie,
Wärmeenergie; Höhen- oder Lage- oder potentielle Energie (Stausee), Spannenergie
(Trampolin, Bogenschießen), Bewegungsenergie (fahrendes Auto).
Energie ist in ganz verschiedenen Formen vorhanden und kann sich vielfältig umwandeln.
Wir befassen uns im Folgenden nur mit mechanischen Energieformen.
Versuche
Dorn-Bader S. 66/67
Versuch V1:
Eine Kugel hängt von der Decke
herab und wird aus der Gleichgewichtslage A nach B ausgelenkt, z. B. direkt bis vor die Nasenspitze eines „Versuchskaninchens“. Die Kugel ist jetzt gegenüber A um die Strecke h angehoben. Lässt man die Kugel los, so
schwingt sie zur GleichgewichtsC
lage zurück und steigt dann auf
v=0
B
der anderen Seite (fast) gleich
A
h
hoch bis C und kommt wieder
NN
(fast) nach B zurück. Es besteht
h=0
keine Gefahr für das „Versuchskaninchen“.
Man sagt, die Kugel habe in B und C gegenüber dem Niveau von A Höhenenergie
(auch Lageenergie oder potentielle Energie genannt). Wie bei der Angabe einer Höhe bezieht man die Lageenergie auf ein Ausgangsniveau (Nullniveau, NN).
In Punkt A hat die Kugel maximale Geschwindigkeit, ist aber gegenüber dem Nullniveau nicht angehoben, hat also keine Lageenergie. Die Kugel hat in A nur Bewegungsenergie (kinetische Energie). Zwischen B und A bzw. zwischen A und C besitzt die Kugel sowohl Lage- als auch Bewegungsenergie. Es finden während der Pendelschwingung laufend Energieumwandlungen statt.
Versuch V2:

v
0
unbelastete
Feder
Gleichgewichtslage
Nullniveau
C
A
B
Wird die Kugel im tiefsten Punkt B losgelassen, so hat sie dort keine Geschwindigkeit. Man legt sinnvollerweise in den Punkt B auch das Nullniveau der Lageenergie.
Die Kugel hat in B weder Lage- noch Bewegungsenergie. Die Energie steckt vollständig in der gespannten Feder als Spannenergie. Beim Auf- und Abschwingen der
Kugel wandeln sich laufend Spannungsenergie, Bewegungsenergie und Lageenergie
ineinander um.
Merke:
Lageenergie, Bewegungsenergie und Spannenergie bezeichnet man als mechanische
Energieformen oder mechanische Energien.
9.2. Energieerhaltung im abgeschlossenen System
Gedankenspiel:
Auf einer vollständig abgeschlossenen Insel soll eine bestimmte Geldmenge im Umlauf zwischen Einwohnern und Banken sein. Die Geldsumme ist immer konstant!
Wie bei dieser eingeschlossenen Geldmenge können wir bei den Versuchen V1 und
V2 einen Bereich eingeben, in dem alle Körper sind, die während des Versuchs Energie austauschen. Welche Körper müssen z. B. beim Fadenpendel berücksichtigt werden?
Um diesen Bereich kann man in Gedanken eine Hülle legen, die nichts durchlässt.
Dieses Gebilde nennt man ein energetisch abgeschlossenes System.
Bei den Schwingungen kommen die Pendelkörper infolge der Reibungsvorgänge allmählich zur Ruhe. Warum?
Versuch V4
Auf einem Luftkissengleiter werden kleine Stahlkugeln transportiert, die fest am Boden haften. Nach einem vollelastischen Stoß hat der Gleiter betragsmäßig dieselbe
Geschwindigkeit wie vor dem Stoß.

Sind gleich viele Stahlkugeln frei beweglich in einer Schale auf dem Luftkissengleiter, so bewegt sich nach dem Stoß der Gleiter merklich langsamer. Dafür schwirren
die Kugeln regellos in den Schalen herum. Die Kugeln haben einen Teil der Energie
übernommen. Auch die Kugeln kommen zur Ruhe. Die Energie „versickert“ in einer verstärkten Bewegung der Moleküle. Die innere Energie der Körper ist größer
geworden.
Merke:
1. Energie kann ihre Form wandeln. Mechanische Energieformen sind Lageenergie, Bewegungsenergie und Spannenergie.
2. Ein Bereich, der mit seiner Umgebung keine Energie austauscht, nennt man ein
energetisch abgeschlossenes System.
3. In einem abgeschlossenen System bleibt die Energie erhalten.
9.3. Messen und Berechnen von Energie
Gedankenexperiment:
An einem Gebäude sind zwei
Kräne im Einsatz, die mit
Diesel betrieben werden. Die
Menge an verbrauchtem Dieselöl kann man als Maß für
die Lageenergie der angehobenen Last ansehen (auch
wenn ein bestimmter Teil der
Ölenergie als Wärme abgeführt wird).
• Hebt nur einer der Kräne einen Eisenträger (G = 50000 N) in den 1. Stock, dann
benötigt er eine bestimmte Menge Öl.
• Hebt dieser Kran dieselbe Last in den 4. statt in den 1. Stock, dann braucht er
die 4fache Ölmenge.
Die Lageenergie ist im 4. Stock 4-mal so groß wie im 1. Stock. Die Lageenergie WL ist
proportional zur Höhe h: WH ∼ h. Als Nullniveau NN, das man beliebig festlegen
kann, ist der Erdboden gewählt.
• Wird ein doppelt so schwerer Eisenträger (G = 100000 N) von zwei Kränen in

den 1. Stock gehoben, dann benötigen sie für die doppelte Gewichtskraft auch
die doppelte Menge an Öl. Der doppelt so schwere Eisenträger besitzt im 1.
Stock auch die doppelt so große Höhenenergie: WL ∼ G
Nach diesen Überlegungen kann die Höhenenergie zu WL = G · h = mgh festgelegt
werden.
Merke:
1. Die Lageenergie eines Körpers mit der Gewichtskraft G in der Höhe h über dem
Nullniveau ist WL = G · h = mgh.
2. Die Einheit der Energie ist 1 Joule (1 J).
Lässt man einen Körper aus der Höhe h frei fallen, dann verliert er ständig Höhenenergie, gewinnt aber Bewegungsenergie. Fällt er um die Strecke h, so nimmt seine
1
1
1
Höhenenergie um m · g · h = m · g · g · t2 = m · ( g · t)2 = m · v2 ab. aus der
2
2
2
verschwundenen Höhenenergie WL ist Bewegungsenergie WB entstanden.
Merke:
Ein Körper der Masse m und der Geschwindigkeit v hat die Bewegungsenergie WB =
1 2
mv .
2
Unterscheide zwischen Energie und Kraft!
Je höher der Kran die Last hebt, desto mehr Energie wird aus Dieselöl in Höhenenergie umgesetzt. Stellt der Kranfahrer den Motor ab und legt eine Sperrklinke ein, so
bleibt die Last in einer bestimmen Höhe hängen, ohne dass weiter Energie umgesetzt
wird. Trotzdem muss der Kran Kraft aufwenden, um die Last auf gleicher Höhe zu
halten!
Beispiel einer Energiebilanz:

Fgl
h/ m
WL = 4500 J WB = 0 J
WL = 4000 J WB = 500 J
40
30
WL = 2500 J WB = 2000 J
20
10
1
2
3
WL = 0 J WB = 4500 J
t/ s
1
Ein Körper fällt frei aus 45 m Höhe. Die Summe WL + WB = mgh + mv2 bleibt kon2
stant.
Merke:
Wenn in einem abgeschlossenen System nur Höhen- und Bewegungsenergie auftreten, bleibt die Summe WL + WB immer konstant und gibt die Energie des Systems
an.
Versuch Dorn-Bader S. 69 V1
Messwerte:
Kugeldurchmesser:
d = ∆s = 5 cm
Kugelmasse:
m = 500 g
HÃöhenunterschied: h = 76 cm − 16 cm = 60 cm
Dunkelzeit:
∆t = 0,0145 s
∆s
m
Geschwindigkeit:
v=
≈ 3,45
∆t
s
Lageenergie:
WL = mgh = 0,5 · 9,8 · 0,60 J ≈ 2,94 J
1
Bewegungsenergie:
WB = mv2 = 2,98 J
2
Ergebnis:
Im Rahmen der Messfehler ist WL = WB .
Übungen Dorn-Bader S. 71 Nr. A1 - A5
9.4. Spannenergie
Versuch

∆t
F = Ds0
Gleichgewichtslage
C
s0
unbelastete
Feder
A
G
Nullniveau
B
s = 2s0
0
Wir hängen an eine entspannte Feder mit
der Federkonstanten D ein Wägestück der
Masse m und lassen es vorsichtig in die
Gleichgewichtslage absinken. Die Feder
ist dann um die Strecke s0 gedehnt und die
Federkraft F = Ds0 (vgl. Kap ??) hält der
Gewichtskraft G = mg das Gleichgewicht.
Es gilt mg = Ds0 .
Hängen wir das Wägestück an die entspannte Feder und lassen es fallen, dann
schwingt es bis zum unteren Umkehrpunkt durch. Dabei wird die Feder um s =
2s0 ausgelenkt.
Legen wir in den unteren Umkehrpunkt das Nullniveau der Höhenenergie, so ist
dort die gesamte Höhenenergie WL = mgh = mgs in Spannenergie WSp der Feder umgewandelt worden. Da die Energie erhalten bleibt, gilt für die Spannenergie:
1
WSp = mgs = Ds0 · s = D · s2
2
Merke:
Dehnt man eine Feder mit der Federkonstanten D aus der entspannten Lage um die
Strecke s, dann hat sie die Spannenergie
WSp =
1 2
Ds
2
Der Energieerhaltungssatz der Mechanik lautet damit:
Merke:
Die Summe aus Lage-, Bewegungs- und Spannungsenergie ist bei reibungsfrei verlaufenden mechanischen Vorgängen in einem abgeschlossenen System konstant:
1
1
WL + WB + WSp = mgh + mv2 + Ds2 = konstant
2
2
Versuch Dorn-Bader V2 S. 71 Bild B1
An eine Feder mit der Federkonstanten D wird ein Körper der Masse m aus Eisen
gehängt und nach unten gezogen. Dort wird er von einem Elektromagneten festgehalten (Zustand I). Hierbei ist die Feder um s1 verlängert. In diesen Zustand I legen
wir das Nullniveau der Lageenergie. Schaltet man den Magnetstrom aus, dann wird
der Körper von der Feder nach oben beschleunigt. In einer beliebigen Höhe h2 über
dem Nullniveau NN ist eine Lichtschranke befestigt, deren Lichtstrahl von einem
seitlich an den Körper angebrachten Flügel der Höhe ∆s = 0,02 m während der Zeit

∆t unterbrochen wird. Dadurch kann die Geschwindigkeit des Körpers in der Höhe
h2 (= Zustand II) bestimmt werden. Die Feder ist dabei um s2 = s1 − h2 verlängert.
Mit diesen Daten kann man die einzelnen Energiebeträge der Höhen- (WL ), Bewegungs(WB ) und der Spannenergie (WSp ) im Zustand II ermitteln und mit der Energie im
Zustand I vergleichen.
Messergebnisse
Körpermasse:
Federkonstante:
Frage: Wie kann man D messen?
m = 0,5 kg
N
D = 22
m
Zustand I
Verlängerung der Feder:
s1 = 0,42 m
Gesamtenergie:
WI = WSp =
Zustand II
Höhe über NN:
Unterbrechungszeit des Lichtstrahls:
Höhe der Fahne:
Geschwindigkeit:
Bewegungsenergie:
Lageenergie:
Spannenergie:
Gesamtenergie:
1 2
Ds = 1,94 J
2 1
h2 = 0,13 m
∆t = 0,0159 s
∆s = 0,02 m
m
∆s
≈ 1,26
v=
∆t
s
1 2
WB = mv = 0,4 J
2
WL = mgh2 = 0,64 J
1
WSp = Ds22 = 0,93 J
2
WI I = WB + WL + WSp = 1,97 J
Im Rahmen der Messgenauigkeit findet man, dass die Energiesummen WL + WB +
WSp in beiden Zuständen gleich sind!
9.5. Lösung von Problemen mit Hilfe des Energieerhaltungssatzes
Oft lassen sich physikalische Probleme leichter mit Hilfe des Energieerhaltungssatzes, d. h. durch ein Bilanzdenken lösen als durch Bestimmung der Kräfte.
Beispiel Dorn-Bader S. 71 und S. 72!!
Übungen Dorn-Bader S. 73 A1 bis A9

s
9.6. Energieübertragung durch Arbeit
Arbeitsauftrag Dorn-Bader S. 74 a) bis d)
Untersuche die Energieübertragung bei den verschiedenen Varianten der Beladung
des LKW.
Auch wenn z. B. ein Auto der Masse m durch eine (konstante) Kraft F beschleunigt
wird, gilt:
1 2
1
1
Fs · s = (m a) ·
at = ma2 t2 = mv2
2
2
2
d. h. das Produkt Fs · s aus der in Wegrichtung am Auto angreifenden Kraft Fs und
dem Weg s ist genauso groß wie die Zunahme der Bewegungsenergie des Autos.
Merke:
Arbeit ist die mithilfe einer Kraft von einem System auf ein anderes übertragene
Energiemenge W.
Ist die in Richtung des Verschiebungsweges s wirkende Kraft Fs konstant, so ist die
Arbeit das Produkt aus Fs und s: W = Fs · s.
Wenn die Kraft F, welche an einem Körper
angreift, und der Weg s, entlang dem sich
der Körper bewegt, verschiedene Richtungen haben, dann zerlegt man die Kraft F in
eine Komponente Fs in Wegrichtung und
F2
eine Komponente F2 senkrecht dazu. Den
F
Körper beschleunigt nur die Komponente
ϕ
Fs
Fs . Nur mit dieser Kraft Fs wird Energie
auf den Körper übertragen.
Es gilt: W = Fs · s = F · s cos ϕ, wenn ϕ
der Winkel zwischen den Richtungen von
F und s ist.
Wie berechnet man die Arbeit, wenn Fs nicht konstant ist?
Wird eine Feder mit der Federkonstante D um die Strecke s gedehnt, dann steckt
1
in ihr die Spannenergie WSp = Ds2 . Berechnet man die an der Feder verrichtete
2
Arbeit mit der Formel W = F · s, so erhält man mit F = D · s (hookesches Gesetz) das
Ergebnis W = D · s2 . Da hier die Kraft nicht konstant ist, sondern proportional zu s,
darf die Arbeit nicht einfach mit W = F · s berechnet werden.

v
t Fs
Fs
W
Stellt man die Kraft Fs und den
Weg s in einem Fs − s-Diagramm
dar, dann wird deutlich, dass die
Fläche unter der Fs − s-Kurve der
verrichteten Arbeit entspricht!
W
s
s
9.7. Erhöhung der inneren Energie durch Reibungskräfte
Beispiel:
Ein Autofahrer bremst sein Fahrzeug bei der Geschwindigkeit v0 durch Blockieren
der Räder ab und bringt es zum Stillstand. Die konstante Reibungskraft FR = Fgl
bremst das Auto auf dem Bremsweg S ab. Sie verrichtet die Arbeit FR · S. Dabei wird
1
die Bewegungsenergie aufgezehrt: FR · S = mv20 .
2
Berechnung des Bremsweges
m
v1
v2 = 0
FR = Fgl
s
S
1
W1 = WB = mv21
W2 = 0 J
2
Auf der Bremsstrecke wirkt die (konstante) Reibungskraft FR . Damit wird am Auto
die Arbeit WR = FR · S verrichtet. WR gibt an, welche Energie das Auto durch die
1
Reibung verliert. Es gilt mv21 = FR · S. Mit FR = Fgl = f gl · FN = f gl · m · g auf einer
2
mv21
v2
horizontalen Straße gilt für den Bremsweg S =
= 1 .
2 f gl mg
2 f gl g
Wird das Auto am Hang abgebremst, dann muss die Normalkraft FN = mg cos α
verwendet werden, wenn α die Neigung des Hangs angibt.
Merke: Reibung mit der konstanten Kraft FR entzieht dem System längs des Reibungsweges s die mechanische Energie WR = FR · s und wandelt diese in innere
Energie des Systems um.
Berechnung der Dauer des Bremsvorgangs
Mit Energiebilanzen lässt sich die Dauer des Bremsvorgangs nicht bestimmen. Hier
1
müssen wir die Bewegungsgesetze (s = at2 ; v = at) und die Newtonsche Grund2
gleichung F = m · a verwenden!

Die Bremsdauer entspricht der Zeit, die benötigt würde, um dem Fahrzeug in umgekehrter Richtung mit der Kraft FR = Fgl auf der Bremsstrecke S wieder die Anfangsgeschwindigkeit v1 zu geben. Es wäre eine gleichförmig beschleunigte Bewegung mit
FR
v
v ·m
a=
. Daraus folgt v1 = a · t =⇒ t = 1 = 1
. Die Bremsdauer kann auch mit
m
a
FR
Hilfe des Kraftstoßes F · ∆t = m · ∆v bestimmt werden (vgl. Kapitel Impuls!)
Beispiel Dorn-Bader S. 77
Übungen Dorn-Bader S. 76 Nr. A3, A4, A5; S. 77 Nr. A6 bis A12
9.8. Leistung
In einem KFZ-Schein steht: 85 kW bei 5400 min− 1; d. h. der Motor liefert in der Zeit
∆t = 1 s die Energie ∆W = 85 kJ bei 5400 Umdrehungen pro Minute. Die Leistung
beschreibt also, wie schnell z. B. eine Maschine Energie abgibt. Geschieht dies un∆W
und Mogleichmäßig, so unterscheidet man zwischen mittlerer Leistung P =
∆t
∆W
mentanleistung P = lim
= Ẇ (Ableitung von W nach der Zeit t). Die Einheit
∆t→0 ∆t
J
der Leistung ist 1 Watt: 1 W = 1 . 1 kW = 1 · 103 W. Aus der Leistungseinheit 1 kW
s
folgt die häufig verwendete Energieeinheit 1 kWh = 3,6 MJ.
Ein Motor großer Leistung muss nicht unbedingt auch eine große Kraft ausüben.
∆W
Fs · ∆s
∆s
=
= Fs ·
= Fs · v.
∆t
∆t
∆t
In einem hinreichend kleinen Zeitintervall ∆t können wir die mittlere Geschwindigkeit v durch die Momentangeschwindigkeit v und damit die mittlere Leistung
P durch die Momentanleistung P ersetzen. Somit gilt: P = Fs · v.
Es gilt: P =
Arbeitsauftrag: Dorn-Bader S. 78/79
Erkläre den Zusammenhang P = Fs · v beim Autofahren.
Wieviel Energie braucht ein Mensch pro Tag?
Wie wird der Wirkungsgrad η einer Maschine gemessen?
Merke: Wird die Energie ∆W durch eine Kraft Fs in Richtung der Geschwindigkeit v
übertragen, so ist die Leistung P das Produkt der Kraft Fs und der Geschwindigkeit
v: P = Fs · v.

9.9. Luftwiderstand und cw -Wert
Ein Auto mit der Querschnittsfläche A muss bei der Geschwindigkeit v in der Zeit ∆t
die Luft vom Volumen V = A · ∆s = A · v · ∆t, also der Masse m = ρ · V = ρ · A ·
v · ∆t beiseite schieben. Wir nehmen vereinfacht an, dass alle Luftteilchen die gleiche
Geschwindigkeit u erhalten. Je nach Form des Autos kann man dann annehmen, dass
1
1
die Bewegungsenergie der Luftmasse durch mu2 = m · cw · v2 (Hinweis: u ∼ v ⇒
2
2
u2 ∼ v2 ⇒ u2 = cw v2 ; cw := Widerstandsbeiwert) ausgedrückt werden kann. Ersetzt
man noch die Luftmasse m durch das vom Auto überstrichene Volumen V und die
1
1
Dichte ρ der Luft, dann gilt: WLu f t = cw · ρ · A · ∆t · v3 = cw · ρ · A · v2 · ∆s. Die
2
2
Luftwiderstandskraft FL , gegen welche das Auto ankämpfen muss, errechnet sich
1
somit durch FL = cw · ρ · A · v2 . Der cw -Wert für PKW liegt bei 0,3 bis 0,4.
2
Übungen Dorn-Bader S. 79 Nr. A1 - A5

10. Impulserhaltung
10.1. Beispiele für Stoßvorgänge
• Huckepackflummies
Ein kleiner und ein großer Superball erreichen, wenn sie aus der
gleichen Höhe fallen, nach dem
Aufprall nahezu wieder die Ausgangshöhe.
Legt man den kleinen Ball oben
auf den großen und lässt die Bälle im Huckepack gemeinsam fallen,
so springt der kleine Ball sehr viel
höher zurück als vorher.
• Elastischer Stoß
m2
m1
m1
m2
h
h
m
). Auf diesen lassen wir einen
s
Gleiter gleicher Masse m1 = m2 mit einer Geschwindigkeit v1 stoßen.
m
Ergebnis: Der stoßende Gleiter kommt beim Stoß zum Stehen u1 = 0 . Der
s
gestoßene Wagen fährt mit u2 = v1 weiter.
Auf der Luftkissenbahn ruht ein Gleiter (v2 = 0
Bei einem vollelastischen Stoß gilt die Erhaltung der mechanischen Energie:
1
1
1
1
m1 v21 + m2 v22 = m1 u21 + m2 u22
2
2
2
2
Hinweis:
Wir bezeichnen die Geschwindigkeiten vor dem Stoß mit vi und nach dem Stoß
mit ui .
Der Energiesatz sagt nichts darüber aus, warum z. B. der 1. Gleiter nicht nur
die Hälfte seiner Energie abgibt. Mit dem Energiesatz allein lassen sich die Geschwindigkeiten u1 und u2 nach dem Stoß nicht eindeutig bestimmen.
• Unelastischer Stoß
Auf der Luftkissenbahn werden zwei Gleiter gleicher Masse mit gleich großen
Geschwindigkeiten v1 und v2 gegeneinandergestoßen und bleiben aneinander
haften (= unelastischer Stoß). Beide Wagen kommen nach dem Stoß zur Ruhe
m
u1 = u2 = 0 . Die Knetmasse zwischen den Wagen führt alle mechanische
s
Energie als Wärme ab. Die mechanische Energie bleibt nicht mehr erhalten!

FR
F 10.2.
Herleitung des Impulserhaltungssatzes
F1 auf 2
m2
Bei einem zentralen Stoß gilt in jedem Augenblick das Gesetz actio = reactio. Wählen wir die Richtung der Kräfte oder Geschwindigkeiten nach rechts positiv und
nach links negativ, dann gilt stets
F2 auf 1
m1
F2au f 1 = − F1au f 2
∆v1
∆v
m1 ·
= − m2 · 2
∆t
∆t
m1 · ∆v1 = −m2 · ∆v2
∆v
folgt
∆t
Nach Multiplikation mit der Stoßdauer ∆t
mit F = m · a = m ·
aus ∆v1 = u1 − v1 und ∆v2 = u2 − v2 folgt
geordnet nach u und v
m 1 · ( u1 − v 1 ) = − m 2 · ( u2 − v 2 )
m 1 u1 + m 2 u2 = m 1 v 1 + m 2 v 2
In dieser Gleichung kommen nur noch die Produkte Masse mal Geschwindigkeit vor.
Dem Produkt p = m · v gibt man den Namen Impuls. Die Einheit des Impulses ist
m
= 1 Ns.
dann 1 kg ·
s
Merke:
Impulserhaltungssatz für gerade Stöße:
Die Impulssumme p = m1 v1 + m2 v2 zweier Körper vor dem Stoß ist gleich ihrer
Impulssumme p = m1 u1 + m2 u2 nach dem Stoß.
Der Gesamtimpuls p bleibt beim Stoß erhalten.
Der Impuls darf nicht mit der Bewegungsenergie verwechselt werden. Während der
Impuls sowohl bei einem elastischen wie auch unelastischen Stoß erhalten bleibt,
sinkt die Summe der Bewegungsenergien, wenn der Stoß nicht vollkommen elastisch
ist.
Der Impuls ~p = m ·~v ist ein Vektor in Richtung des Geschwindigkeitsvektors. Auf die
Vektorschreibweise können wir verzichten, wenn wir (oBdA) die Geschwindigkeiten
oder Impulse nach rechts mit positiven Zahlenwerten, nach links mit negativen Zahlenwerten versehen.
Übungen Dorn-Bader S. 82 Nr. A1, A2; S. 83 Nr. A3
10.3. Bestätigungsversuche
Die Bestätigungsversuche werden im Praktikum durchgeführt.

vt 10.4.
Kraftstoß
Beispiel
Wir schieben ein Auto an und versuchen dabei, die
Kraft konstant zu halten. Je größer unsere Kraft ist
und je länger wir schieben, desto größer wird die
Geschwindigkeit des Autos.
Nach der Newtonschen Grundgleichung
∆v
gilt nach Multiplikation mit
F = m·a = m·
∆t
∆t: F · ∆t = m · ∆v = ∆p.
Merke:
Wird ein Körper während der Zeit ∆t durch eine konstante Kraft F beschleunigt, dann
erfährt er die Impulsänderung ∆p = F · ∆t.
Das Produkt F · ∆t nennt man Kraftstoß.
F/N
400
300
200
∆t′
100
1
2
3
4
5
6
7
8
Wenn die Kraft beim Anschieben des Autos nicht
konstant ist, dann können wir die Impulsänderung
aus dem t − F-Diagramm ermitteln. Während eines kleinen Zeitintervalls ∆t′ ist die Kraft F hinreichend konstant und das Auto erfährt den Kraftstoß
F · ∆t′ . Die getönte Rechtecksfläche gibt den Kraftstoß F · ∆t′ an. Die Fläche des t-F-Diagramms kann
aus lauter solchen Streifen zusammengesetzt werden. Die gesamte Fläche unter dem t-F-Diagramm
t/s
entspricht also der gesamten Impulszunahme ∆p
des Autos.
Berechne die Impulsänderung des Autos. Welche Geschwindigkeit hat das Auto (Masse 600 kg),
wenn es aus dem Stand beschleunigt wurde?
Arbeitsauftrag Buch S. 87; Sportunterricht!
Wie kann ein Sportler aus dem Stand beim senkrechten Sprung eine maximale Höhe
erreichen?
10.5. Kraftberechnung mit Hilfe der Impulsänderung
∆p
ermittelt werden. Man braucht also nur zu wissen,
∆t
um wie viel sich der Impuls p der betrachteten Materie während der Zeit ∆t insgesamt ändert. Welche Beschleunigungen dabei die einzelnen Masseteilchen erfahren,
braucht nicht bekannt zu sein.
Die Kraft kann auch mit F =

Beispiele 1, 3 Dorn-Bader S. 88/89
Übungen Dorn-Bader S. 89 Nr. A1 - A6, S. 94 Nr. A1 - A5, A8, A9
11. Kreisbewegungen
Dorn-Bader S. 95 ff
11.1. Kreisbewegungen in unserer Umgebung
Volksfest: Kettenkarusell, Rotor, Loopingbahn (S. 95, 102, 103)
Verkehr: Kurvenfahren
Sport: Hammerwurf, Skateboard
Merke
Wir beschränken uns auf Kreisbewegungen von Körpern, deren Ausdehnung gegenüber dem Radius r der Kreisbahn klein ist.
11.2. Grundbegriffe
Versuch
Ein Tischtennisball an einem Faden kreist gleichmäßig in einer senkrechten Kreisbahn. Im abgedunkelten Raum wird der Ball mit einem Stroboskop in gleichen Zeitabschnitten ∆t beleuchtet. Man sieht, dass er gleichgroße Kreisbögen ∆s durchläuft.
Also ist der Betrag der Geschwindigkeit v =
gleichförmigen Kreisbewegung.
∆s
konstant. Man spricht von einer
∆t
Die Zeit für einen Umlauf auf der Kreisbahn nennt man Umlaufdauer T.
Je kürzer die Umlaufdauer T des gleichförmig kreisenden Balls ist, desto häufiger
durchläuft er in einer Sekunde den Kreis.
n
Zahl der Umläufe
1
Seine Drehfrequenz f = =
= wird größer.
t
Zeit
T
Der Betrag der Geschwindigkeit v lässt sich damit auch durch folgende Terme aus∆s
2πr
drücken: v =
=
= 2πr f
∆t
T

2π
∆ϕ
=
= 2π f
∆t
T
eingeführt. Sie beschreibt die Geschwindigkeit eines Massenpunktes auf dem Einheitskreis (vgl. Bogenmaß des Winkels!). Damit gilt für den Betrag der Geschwindigkeit v eines Massenpunktes auf einem Kreis mit dem Radius r: v = ω · r!
Bei Kreisbewegungen wird häufig die Winkelgeschwindigkeit ω =
Merke:
1. Die Kreisbewegung eines Massenpunktes heißt gleichförmig, wenn der
Betrag v seiner Geschwindigkeit konstant ist.
2. Die Zeit, die der Massenpunkt für einen Umlauf auf der Kreisbahn benötigt, nennt man Umlaufdauer T.
3. Für die Drehfrequenz f gilt
n
Zahl der Umläufe
1
f = =
=
t
Zeit
T
∆ϕ
2π
4. Für die Winkelgeschwindigkeit gilt ω =
=
= 2π f . Sie be∆t
T
schreibt den Betrag der Geschwindigkeit eines Massenpunktes auf dem
Einheitskreis.
2πr
∆s
=
=
5. Formeln für den Betrag v der Geschweindigkeit: v =
∆t
T
2πr f = ω · r
11.3. Zentripetalkraft
Die Bewegungsrichtung des rotierenden Tischtennisballs ändert sich ständig. Der Geschwindigkeitsvektor ~v zeigt in jedem Punkt der Kreisbahn in die Richtung der jeweiligen Bahntangente und gibt die momentane Bewegungsrichtung des Körpers an.
Merke:
Bei einer gleichförmigen Kreisbewegung bleibt nur der Betrag der Geschwindigkeit
gleich. Die Richtung der Geschwindigkeit steht immer senkrecht zum Radius und
ändert sich dauernd.
Schleudert man einen Ball an einer Schnur im Kreis herum, dann spürt man, dass auf
den Ball ständig eine Kraft zum Kreismittelpunkt hin wirken muss, damit der Ball
auf einer Kreisbahn bleibt. Man nennt diese Kraft Zentripetalkraft Fz .
Versuch V1 Dorn-Bader S. 96
Wir zwingen einen an einen Faden gebundenen Gummistopfen auf eine Kreisbahn.
Schneiden wir den Faden mit einer Rasierklinge durch, dann fliegt der Gummistopfen tangential weg! Es fehlt die äußere Kraft, die den Stopfen auf die Kreisbahn
zwingt.
Problem: Wie groß ist die Zentripetalkraft Fz ?

∆tWenn wir annehmen, dass auch für Fz die Grundgleichung der Mechanik: Fz = m · az
gilt, dann müssen wir die Beschleunigung az bestimmen.
~v
a~z
~r
~v
~r
~v
~r
~v
~v
a~z
a~z
~v
~v
~r
a~z
~v
Wir beschreiben die gleichförmige Kreisbewegung eines Massenpunktes mit einem
rotierenden Radiusvektor ~r. Während eines Umlaufs rotiert der Radiusvektor ~r um
2π. Da der Geschwindigkeitsvektor ~v in jedem Punkt der Kreisbahn senkrecht zum
Radiusvektor ~r ist, durchläuft auch er gerade einen ganzen Kreis. Wenn der Geschwindigkeitsvektor ~v die zeitliche Änderung des Radiusvektors ~r angibt, dann ergibt sich der Vektor der Zentralbeschleunigung a~z aus der zeitlichen Änderung des
Geschwindigkeitsvektors ~v . Während der Umlaufdauer T dreht sich ~r und ~v gerade
2πv
v2
2πr
und a =
=⇒ a = .
einmal im Kreis; d. h. v =
T
T
r
Für den Betrag der Zentripetalkraft Fz ergibt sich damit Fz =
mv2
.
r
Versuch
Abbildung Dorn-Bader S.99 (V1)
Ein Wagen kann sich auf einer Schiene bewegen und ist mit einem Faden über eine
Umlenkrolle an einem Kraftmesser befestigt. Lässt man die Schiene gleichförmig rotieren, so beschreibt der Wagen eine Kreisbahn. An der Schiene kann man den Radius
r der Kreisbahn und am Kraftmesser die Zentripetalkraft Fz ablesen.
Messwerte:

Wagenmasse
Kreisradius
m
r
= 0,15 kg
= 0,16 m
20 Umläufe
20 · T = 22,7 s ⇒ T = 1,14 s und v =
Zentripetalkraft (exp.)
Zentripetalkraft (theor.)
Fzex = 0,75 N
Fzth = 0,74 N
2rπ
T
Merke:
1. Die gleichförmige Kreisbewegung ist eine beschleunigte Bewegung,
für die die Grundgleichung der Mechanik gilt.
2. Zentripetalbeschleunigung az und Zentripetalkraft Fz sind in jedem
Punkt der Bahn zum Kreismittelpunkt hin gerichtet.
v2
mv2
3. Es gilt: az =
und Fz = m · az =
r
r
11.4. Zentrifugalkraft
In der Umgangssprache wird bei Kreisbewegungen meistens die Zentrifugalkraft erwähnt. Wenn man mit dem Auto in die Kurve fährt, wird man nach außen gedrückt.
Wir verspüren als mitbeschleunigter Beobachter eine Zentrifugalkraft. Der außenstehende Beobachter ist in einem sogenannten Inertialsystem, stellt fest, dass der Autofahrer auf die Kreisbahn durch eine Zentripetalkraft gezwungen wird. Beide Kräfte
haben denselben Betrag! Welche Kraft betrachtet wird, hängt letztlich vom Bezugssystem ab. Wir verwenden in der Regel nur die Zentripetalkraft.
Übungen Dorn-Bader S. 99 Nr. A1 - A7
11.5. Verkehrsphysik 2
Dorn-Bader S. 100/101
Arbeitsauftrag
• Fahrzeuge in einer nicht überhöhten Kurve
Wie groß darf die Geschwindigkeit v eines Autos höchstens sein, damit es eine
nicht überhöhte Kurve durchfahren kann?
Bedingung: Fz 6 Fh,max
• Fahrzeuge in einer überhöhten Kurve
Beachte die allgemein gültige Regel:
Bildet man die Summe aller am Fahrzeug angreifenden äußeren Kräfte, so muss
die Zentripetalkraft Fz entstehen!

• Schneiden einer Kurve - Bremsen in der Kurve
Übungen S. 101 Nr. A1 - A4
11.6. Physik auf dem Volksfest
Dorn-Bader S. 102/103
• Kettenkarussell
ϕ
ℓ
ϕ
r0
F
x
Fz
G
Der Sitz des Kettenkarussells
rotiert auf einer Kreisbahn vom
Radius: r = r0 + x, wobei x =
ℓ · sin ϕ vom Auslenkungswinkel ϕ abhängt. Die schräg nach
oben gerichtete Kraft F, welche
die Kette aufbringt, und die Gewichtskraft G bringen die Zentripetalkraft Fz auf. F ist so groß,
dass Fz waagrecht verläuft. Aus
dem Kräftedreieck kann man
eine Beziehung zwischen der
Gewichtskraft G und der Zentripetalkraft Fz ablesen.
Fz
mv2
v2
tan ϕ =
=
=
G
rmg
rg
• Rotor

Fh
FN
Fz
G
In der Trommel des um seine
vertikale Achse rotierenden Rotors bleibt ein Körper an der
Wand hängen, wenn die Haftkraft Fh,max mindestens so groß
wie die Gewichtskraft G ist.
Die Wand übt auf den Körper die Zentripetalkraft Fz aus.
Der Körper reagiert mit einer
gleichgroßen Normalkraft FN
auf die Wand. Damit ergibt sich
eine Haftkraft Fh,max = f h · FN .
Der Körper bleibt also hängen,
wenn gilt:
mg 6 f h · FN oder mg 6 f h · Fz =
• Loopingbahn oder rotierende Milchkanne
vo
Damit die Kanne samt Milch
auf einer Kreisbahn läuft, muss
sie andauernd in Richtung auf
den Kreismittelpunkt hin beschleunigt werden. Macht man
die Rotationsgeschwindigkeit
so groß, dass die notwendige
Zentripetalkraft gerade so groß
wie die Gewichtskraft ist, dann
muss man im oberen Punkt der
Kreisbahn keine zusätzliche
Kraft zum Kreismittelpunkt
hin aufbringen. Im untersten
Punkt der Kreisbahn muss man
allerdings außer der Zentripetalkraft Fz auch noch die
Gewichtskraft G aufbringen.
G
Fz
F
M
F
Fz
vu
G
Übungen S. 103 Nr. A1 - A4; S. 104 Nr. A1 - A7

f h mv2
r
12. Gravitation und Planetenbewegung
Dorn-Bader S. 105 ff
12.1. Vermessung von Sonne, Erde und Mond
Arbeitsauftrag
• Wie groß ist die Erde?
• Welchen Abstand hat der Mond von der Erde?
• Welchen Abstand hat die Erde von der Sonne?
Merke:
Der Erdradius beträgt R = 6400 km
Der Mond ist vom Erdmittelpunkt 60 Erdradien = 384 000 km entfernt.
Die Sonne ist 150 · 106 km von der Erde entfernt.
12.2. Newtonsches Gravitationsgesetz
Newton hatte die revolutionäre Idee, dass der Mond für seine Kreisbahn genauso
eine Zentripetalkraft braucht wie irdische Körper.
Gedankenexperiment:
Da wir die Mondmasse nicht kennen, berechnen wir die Zentripetalkraft FZ für einen Stein der
Masse m = 1 kg, der als Minimond im Abstand r = 60 R um
die Erde kreist. Sie müsste den Be4π 2 mr
m · v2
=
=
trag FZ =
r
T2
0,00272 N haben (Umlaufdauer
des Mondes T = 27,3 Tage). Diese Kraft ist in Richtung auf den
Erdmittelpunkt gerichtet. Es handelt sich um eine Anziehungskraft durch die Erde.
m = 1 kg
60 R
FZ
m = 1 kg
R
Erde
Mondbahn
Bekanntlich zieht die Erde an ihrer Oberfläche, d. h. im Abstand R, einen Stein der
Masse 1 kg mit 9,81 N an. Diese Kraft ist etwa 3600 = 602 mal größer. Newton schloss

daraus, dass die Kraft umgekehrt proportional zum Quadrat des Abstandes der Mas1
mv2
senmittelpunkte ist: F ∼ 2 . Weiterhin folgerte er aus FZ =
, dass diese Anzier
r
m
hungskraft auch proportional zur Masse m des kreisenden Körpers ist: F ∼ 2 .
r
Stellen wir in Gedanken neben die Erde eine zweite, genau gleiche, dann dürfen wir
erwarten, dass beide zusammen (doppelte Masse M) auf den Mond auch die doppelte Kraft F ausüben. Die Anziehungskraft ist daher auch proportional zu der Masse M
m·M
. Dieses Gesetz wird dann allgemein zwischen zwei
des Zentralkörpers: F ∼
r2
Massen gelten.
Damit ergibt sich das
Newtonsches Gravitationsgesetz:
Alle Körper üben aufeinander Gravitationskräfte aus. Zwei kugelförmige
Körper der Masse m und M, deren Mittelpunkte voneinander den Abstand r
haben, ziehen sich mit der Gravitationskraft F an:
m·M
F=γ 2
r
m3
γ heißt Gravitationskonstante. Sie hat den Wert γ = 6,67 · 10−11
kgs2
Der Wert der Gravitationskonstanten lässt sich bestimmen, wenn man die Anziehungskraft zwischen zwei Massen m und M misst. Dies kann man mit der Gravitationsdrehwaage machen.
Versuch Dorn-Bader S. 109
Übungen Dorn-Bader S. 108 Nr. A1 - A4; Beispiel S. 108, Nr. 1 und 2!
12.3. Die Kepler Gesetze
Aus präzisen Messungen des Dänen Tycho Brahe (1546 - 1601) fand Kepler (1571 1630), dass die Planeten um die Sonne auf Ellipsenbahnen laufen, in deren einem
Brennpunkt die Sonne steht. Er formulierte drei Gesetze.

Erstes Kepler-Gesetz:
Planeten bewegen sich auf Ellipsen, in deren einem Brennpunkt die Sonne
steht.
Zweites Kepler-Gesetz:
Der Fahrstrahl Planet - Sonne überstreicht in gleichen Zeiten gleiche Flächen.
Drittes Kepler-Gesetz:
Die Quadrate der Umlaufdauern T1 und T2 zweier Planeten um die Sonne
verhalten sich wie die dritten Potenzen der großen Halbachsen a1 und a2 .
a31
T12
=
T22
a32
Die Keplergesetze gelten entsprechend für beliebige Trabanten um Zentralkörper.
Übungen Dorn-Bader S. 113 Beispiele 1 und 2, Übungen A1 - A9
Computersimulationen und Projekte Dorn-Bader S. 114 - 117
Hintergrundinfos Dorn-Bader S. 123 - 127
