Kennlinien elektrischer Leiter

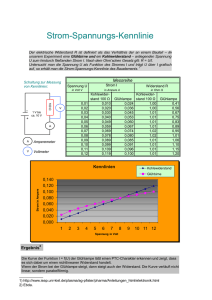
Anleitung zum Physikpraktikum
für Oberstufenlehrpersonen
Kennlinien elektrischer Leiter (KL)
Frühjahrssemester 2018
Physik-Institut der Universität Zürich
Inhaltsverzeichnis
10 Kennlinien elektrischer Leiter (KL)
10.1 Einleitung . . . . . . . . . . . . . . .
10.1.1 Ziel des Versuches . . . . . .
10.2 Theoretischer Teil . . . . . . . . . .
10.2.1 Metallische Leiter . . . . . .
10.2.2 Halbleiter . . . . . . . . . . .
10.2.3 Lichtabhängige Widerstände
10.3 Experimenteller Teil . . . . . . . . .
10.3.1 Aufgabenstellung . . . . . . .
10.3.2 Durchführung . . . . . . . . .
10.3.3 Auswertung . . . . . . . . . .
10.4 Anhang . . . . . . . . . . . . . . . .
10.4.1 Einfluss der Innenwiderstände
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
. . . . . . . . . . . . .
von Messinstrumenten
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
10.1
10.1
10.2
10.2
10.2
10.2
10.5
10.5
10.5
10.5
10.7
10.9
10.9
10
4.2
4.2.1
4.2.2
10.1
Kennlinien elektrischer Leiter (KL)
Vorlesungsabschnitt 4, Elektrizität und Magnetismus
Stationäre elektrische Ströme
Bewegte Ladungen - Ströme
Spannungsquellen, Strom - Spannungscharakteristiken, Kirchhoff’sche Gesetze
Einleitung
Legen wir an einen elektrischen Leiter eine Spannung V an, so fliesst ein Strom I. Als Widerstand
des Leiters wird der Quotient aus Spannung und Strom definiert:
R = V /I
Einheit: 1 V/1A = 1 Ohm = 1 Ω
(10.1)
Der Widerstand hängt vom Material und von der Geometrie des Leiters ab. Im einfachsten Fall
ist der Strom proportional zur angelegten Spannung, der Widerstand also konstant. In diesem
Fall redet man von einem “Ohm’schen” Widerstand, es gilt das Ohm’sche Gesetz:
R = konst.
bei konstanter Temperatur T
(10.2)
In Wirklichkeit ist diese einfache Proportionalität nie exakt vorhanden, sondern der Strom hängt
in viel komplizierterer Weise von der angelegten Spannung ab. Die Eigenschaften solcher Leiter
werden grafisch, in Form von Kennlinien oder sog. Charakteristiken, welche den Strom als
Funktion der Spannung darstellen, gegeben.
I(V)
I(V)
I2
I1
V1
V2
V
V
Abbildung 10.2: Kennlinie für einen Leiter
mit konstantem “Ohm’schen” Widerstand.
Abbildung 10.1: Kennlinie eines elektrischen Leiters.
In der in Abbildung 10.1 dargestellten Kennlinie ist R = V /I nicht konstant, es gilt R1 =
V 1/I1 > R2 = V 2/I2. Der Widerstand nimmt mit zunehmender Spannung ab. Ist die Kennlinie
eine Gerade durch den Nullpunkt, wie in Abbildung 10.2 dargestellt, so ist R = konstant
(Ohm’sches Gesetz).
10.1
10.1.1
Ziel des Versuches
In diesem Versuch wollen wir Kennlinien verschiedener Leitertypen kennen lernen. Ihre Form
liefert Informationen über die dabei vorkommenden Leitungsmechanismen. Dabei geht es um:
• Elektrische Stromkreise
• die Regeln von Kirchhoff
• den elektrischen Widerstand verschiedener Elemente
• das Ohm’sche Gesetz
• Messen von Spannung und Strom
• Kennlinien verschiedener Elemente
10.2
10.2.1
Theoretischer Teil
Metallische Leiter
Die Leitfähigkeit von Metallen und ihren Legierungen kommt durch die freien Elektronen, die
im Ionengitter leicht beweglich sind, zustande. Bei konstanter Temperatur ist der Widerstand
unabhängig von der Spannung und es gilt das Ohm’sche Gesetz. Wird aber die Temperatur
nicht durch Kühlung konstant gehalten, so bewirkt die beim Stromdurchgang erzeugte Wärme
Q = I · V · t eine Temperaturerhöhung des Leiters (vgl. Toaster). Dabei nimmt der Widerstand
im Allgemeinen zu.
Im einfachsten Fall hängt R linear von der
Temperatur ab. Ist T die absolute Temperatur,
dann gilt:
R
R = R0 (1 + αT )
Der Temperaturkoeffizient
α=
1 dR
·
R0 dT
(10.3)
gibt die relative Widerstandsänderung pro Grad
Temperaturänderung an.
T
Abbildung 10.3: Lineare Abhängigkeit
des Widerstandes von der Temperatur.
Für reine Metalle ist α = 1/273 pro Grad ≃ 0.4% pro Grad. Durch Verwendung von Legierungen
kann α auf etwa 0.002% pro Grad gesenkt werden.
10.2.2
Halbleiter
Die Leitfähigkeiten von Halbleitern liegen zwischen denjenigen von Isolatoren und Metallen. Die
moderne Technik der Herstellung von Halbleitern aus verschiedenen Materialien und Schichten
ermöglicht es sowohl die Zahl der Leitungselektronen als auch ihre Beweglichkeit in weiten
Grenzen zu variieren. Durch Zugabe von Fremdatomen (Verunreinigungen, Dotierungen) kann
die Leitfähigkeit eines Halbleiters stark erhöht werden.
10.2
n-Material
Ins Gitter eines aus 4-wertigen Atomen bestehenden Halbleiterkristalls (z.B. Silizium oder Germanium) werden Atome eines 5-wertigen Elementes eingebaut. In der äussersten Schale dieser
Fremdatome ist ein Elektron zu viel vorhanden. Dieses Elektron ist fast frei beweglich und trägt
zur Leitfähigkeit bei. Man nennt diese Fremdatome Donatoren.
p-Material
Ins Kristallgitter werden Atome eines 3-wertigen Elementes eingebaut. In der äussersten Schale
der Fremdatome fehlt jetzt ein Elektron. Dieses “Loch” ist bestrebt, ein Elektron aufzunehmen.
Wird das Loch durch ein Gitterelektron aufgefüllt, entsteht an anderer Stelle ein Loch; man
spricht von Löcherwanderung. Diese Fremdatome nennt man Akzeptoren.
Anwendungsbeispiele:
Thermistoren
Der Widerstand von Thermistoren ist stark temperaturabhängig. Die sog. NTC (Negative Temperature Coefficient)-Widerstände bestehen aus Oxiden von Cr, Mn, Fe etc.. In Fe2 03 z.B. ist
ein Teil der Fe3+ -Ionen durch Fe2+ - oder Ti4+ -Ionen ersetzt. Mit zunehmender Temperatur
wird das überzählige Elektron des Fe2+ -Iones frei und zum Leitungselektron (n-Material); der
Widerstand des Materials sinkt. Solche Widerstände können zur Temperaturmessung verwendet
werden, da ihre Temperaturkoeffizienten zwischen -2% und -6% pro Grad liegen. Abbildung 10.4
zeigt einige Kennlinien und die Temperaturabhängigkeit eines NTC-Widerstandes.
I(V)
R
T3
T2
T1
T1 < T2 < T3
V
T
Abbildung 10.4: Linkes Bild: Kennlinien eines Thermistors für verschiedene Temperaturen. Rechtes Bild: Abhängigkeit des Widerstandes von der Temperatur.
Halbleiter-Dioden
Eine Halbleiterdiode besteht aus einer p-Material- und einer n-Material-Schicht. Der Kontakt
zwischen p-leitendem und n-leitendem Halbleitermaterial erzeugt den pn-Übergang, welcher
typisch ist für die grosse Gruppe der Halbleiterdioden. Diese finden ihren Einsatz ganz allgemein
in der Gleichrichtung von Spannungen unterschiedlicher Polarität. Eine Kennlinie einer Halbleiterdiode zeigt Abbildung 10.5. Während der Strom in Durchlassrichtung schon bei kleiner Span10.3
I(V)
nung rasch ansteigt, ist er in Sperrrichtung sehr klein, bis zur maximal
zulässigen Sperrspannung, die je nach
Bauart zwischen -10 V und -10 kV liegen kann.
Vz
V
Abbildung 10.5: Kennlinie einer Diode. Vz ist die maximale Sperrspannung.
Durchlassgebiet
Sperrgebiet
Erklärung:
Durchlassrichtung
_
+++_
_ __ _
++
+p + _ n _
I
+ _
V0
Die Löcher des p-Materials werden in die
n-Schicht, die freien Elektronen des n-Materials
in die p-Schicht getrieben, d.h. es fliesst dauernd ein Strom durch die Grenzschicht. Der
Widerstand der Trennschicht ist sehr klein.
Abbildung 10.6: Diode in Durchlassrichtung.
Löcher der p-Schicht und Elektronen der
n-Schicht wandern von der Grenzschicht weg,
d.h. Ladungsträger beider Vorzeichen werden
aus der Grenzschicht entfernt. Es entsteht eine
nichtleitende Zone. Nach dem Aufbau der sog.
Sperrschicht fliesst kein Strom mehr.
Sperrrichtung
+ + + __ __ __
+
+ p++ _ n _
_ +
V0
Abbildung 10.7: Diode in Sperrrichtung.
Für Dioden verwendet man die in der Abbildung 10.8 gezeichneten Symbole. Die Diode leitet,
wenn die Dreiecksspitze in Richtung des Spannungsabfalls zeigt:
+
+
Sperrrichtung
Durchlassrichtung
Abbildung 10.8: Symbol für Diode in Durchlass- und in Sperrrichtung.
10.4
V
Anwendung: Dioden werden z.B. zur
Gleichrichtung von Wechselströmen
benützt.
Abbildung 10.9: Diode als Gleichrichter.
10.2.3
t
R
~
V = V0 sin ω t
I
I
t
Lichtabhängige Widerstände
Lichtabhängige Widerstände bestehen z.B. aus CdS, einem Material in welchem einfallendes
Licht Elektronen freisetzt und so eine Verkleinerung des Widerstandes bewirkt.
10.3
Experimenteller Teil
10.3.1 Aufgabenstellung
1. Die Kennlinien folgender Elemente sollen aufgenommen werden:
• Ohm’scher Widerstand
• Glühlampe
• Diode
2. Qualitative Beobachtung der Widerstandsänderung an einem lichtempfindlichen Widerstand
3. Temperaturabhängigkeit des Widerstands eines Thermistors
10.3.2 Durchführung
Bemerkung: Während einer Mess-Serie sollte der Messbereich der Instrumente nicht geändert
werden. Achtung: Maximalstrom 200 mA nicht überschreiten, sonst brennt die Sicherung durch!
Kennlinien
Ohm’scher Widerstand: Berechnen Sie für den gegebenen Widerstand R den maximalen
Strom Imax für die maximale Spannung Vmax und wählen Sie dann auf dem Ampèremeter den
passenden Messbereich.
Glühlampe: Die maximal zulässige Spannung und der maximale Strom sind angegeben. Wählen
Sie die passenden Messbereiche der Instrumente.
Bemerkung: Die Kennlinien des Ohm’schen Widerstandes und der Glühlampe werden in
Schritten von 5 V aufgenommen. Zu jedem Spannungswert liest man den zugehörigen Strom
ab.
Diode: Die Kennlinie der Diode wird für positive und für negative Spannungen ausgemessen
(Diode umpolen). Der Bereich, in dem die Diode zu leiten beginnt, wird in möglichst kleinen
Schritten (0.02V) ausgemessen.
10.5
Achtung: Der Strom in der Diode steigt plötzlich an. Der maximal zulässige Strom ist angegeben.
Eine Kennlinie wird mit der in Abbildung 10.10 skizzierten Schaltung
aufgenommen. Am Potentiometer
Rp kann eine Spannung zwischen
0 und V0 abgegriffen werden. (Das
Potentiometer ist im Spannungsgerät
eingebaut).
I
V0
RP
RL =
RL
V
- Ohm'scher Widerstand
- Glühlampe
- Diode
Abbildung 10.10: Anordnung zur Messung der Kennlinien.
Stellen Sie die Messwerte in einer übersichtlichen Tabelle zusammen.
Fotowiderstand
Prüfen Sie qualitativ, wie bei fester Spannung (V = 5 V) der Widerstand von der Intensität
des einfallenden Lichtes abhängt, indem Sie den Widerstand verschieden stark mit der Hand
abdecken und den Strom jeweils ablesen.
Thermistor
Bei fester Spannung (V = 10 V) soll der Widerstand aus Strom und Spannung als Funktion der
Temperatur bestimmt werden. Die Versuchsanordnung ist in der Abbildung 10.11 skizziert.
Thermometer
I
NTC
V0
V
Wasser
Dewar
Abbildung 10.11: Anordnung zur Messung der Kennlinie des Thermistors.
Temperaturen: Wählen Sie 5 verschiedene Wassertemperaturen zwischen ca. 10◦ C und 90◦ C.
Wichtig: Vor dem Ablesen des Thermometers muss das Temperaturgleichgewicht abgewartet
werden.
10.6
10.3.3
Auswertung
Kennlinien
• Die drei Kennlinien werden auf Millimeterpapier aufgezeichnet.
• Für jeden Messpunkt (V ,I) wird der Widerstand R = V /I berechnet und R in Funktion
von V grafisch dargestellt (10.12).
I
R
V
Ri = i
Ii
Ii
Ri
Vi
Vi
V
V
Abbildung 10.12: Auswertung der Kennlinien.
Thermistor
• Aus den Strom- und Spannungswerten wird für die 5 Temperaturen der Widerstand berechnet und in Funktion der Temperatur auf Millimeterpapier aufgezeichnet.
• Der Widerstand des verwendeten Thermistors berechnet sich aus
B
R(T ) = Ae T
A und B sind Konstanten
(10.4)
T = Temperatur in Kelvin
Bestimmung von A und B:
Wir logarithmieren obigen Ausdruck (Vergleiche auch Versuch Kapazitäten (C)) :
B
(10.5)
T
Diese Gleichung stellt eine Gerade mit der Steigung B dar, wenn man ln R gegen 1/T aufträgt.
Der Achsenabschnitt ist dann ln A.
ln R = ln A +
ln A kann aus der Abbildung 10.13 herausgelesen oder, bei bereits bestimmtem B, an
einem Punkt R(T ) aus Gleichung (10.4) berechnet werden. Man bestimmt B mit:
ln R
ln A
∆ 1/T
∆ ln R
B=
1/T
∆ ln R
∆1/T
Abbildung 10.13: Steigung der Geraden.
10.7
Bestimmen des Temperaturkoeffizienten α:
Der Temperaturkoeffizient α entspricht der relativen Widerstandsänderung pro Grad Temperaturänderung. Er kann aus dem Widerstand für den Thermistor (10.4) berechnet werden (siehe
auch Gleichung 10.3). Durch Ableiten nach der Temperatur T folgt aus:
B
R = Ae T
dR
dT
1 dR
·
R dT
= Ae
= −
B
T
(
)
1
·B· − 2
T
B
T2
Für den Temperaturkoeffizienten α gilt also:
α=
1 dR
·
R dT
= −
Diese Grösse α soll für T = 300 K berechnet werden.
10.8
B
T2
(10.6)
10.4
10.4.1
Anhang
Einfluss der Innenwiderstände von Messinstrumenten
Jedes Messinstrument hat einen Innenwiderstand. Unter Berücksichtigung dieser Innenwiderstände
erhält man für die Aufnahme einer Kennlinie von kleinen Widerständen, d.h. wenn RiA gegen
R nicht zu vernachlässigen ist, die folgende Schaltung:
RiA
K
I
V0
RP
I
Der gemessene Strom teilt sich im Punkt K
in I1 und I2 auf:
I2
I1
RL
V
RiV
I
= I1 + I2
V
= I1 RiV = I2 RL
Also:
I1 = I2
RL
→0
RiV
falls RiV ≫ RL
Abbildung 10.14: Anordnung zur Messung
kleiner Widerstände RL .
Damit I2 ≃ I wird, muss I1 sehr klein sein, d.h. der Innenwiderstand des Voltmeters muss viel
grösser als R sein. Ein gutes Voltmeter hat einen grossen Innenwiderstand (107 − 108 Ω).
Um grosse Widerstände zu messen, d.h. wenn RiV gegen R nicht zu vernachlässigen ist, verwendet man eine andere Schaltung:
RiA
RL = Element für Kennlinie
I
I
V0
RP
V
RL
RiV
Abbildung 10.15: Anordnung zur Messung
grosser Widerstände RL .
Die gemessene Spannung setzt sich aus dem Spannungsabfall am Ampèremeter und dem Spannungsabfall an RL zusammen:
V = IRiA + IRL
Also:
V
V
− RiA ≃
für RiA ≪ RL
I
I
d.h. der Innenwiderstand des Ampèremeters soll möglichst klein sein. Beim verwendeten Instrument beträgt er etwa 1Ω bei 200 mA Messbereich.
RL =
10.9