Ubungsaufgaben

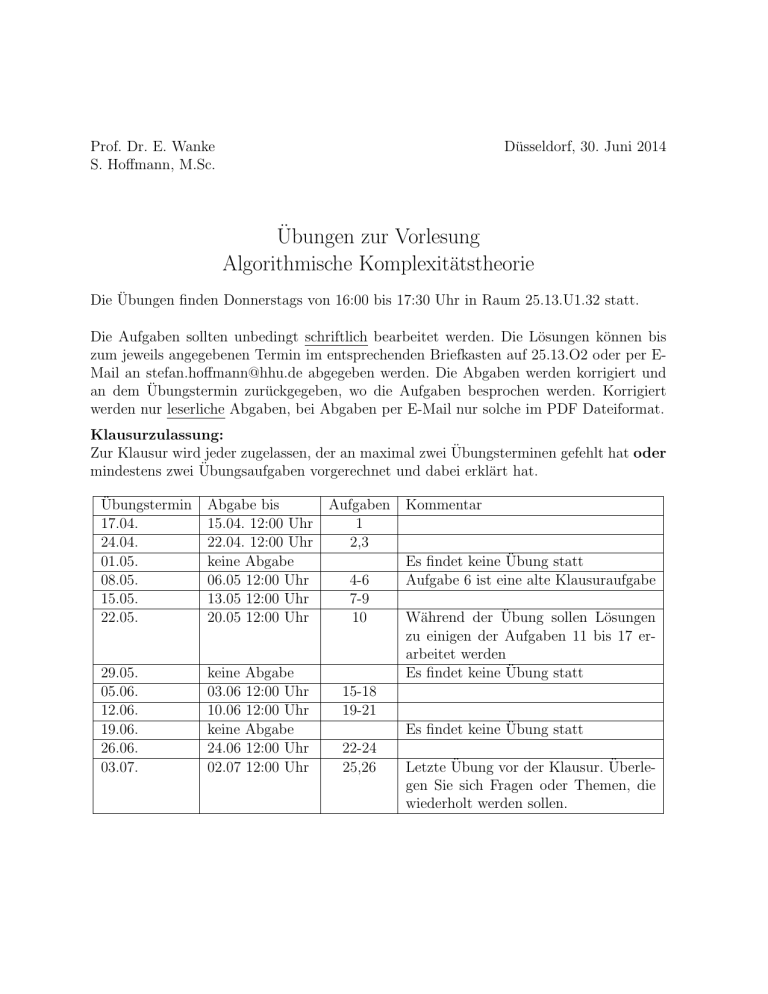
Prof. Dr. E. Wanke
S. Hoffmann, M.Sc.
Düsseldorf, 30. Juni 2014
Übungen zur Vorlesung
Algorithmische Komplexitätstheorie
Die Übungen finden Donnerstags von 16:00 bis 17:30 Uhr in Raum 25.13.U1.32 statt.
Die Aufgaben sollten unbedingt schriftlich bearbeitet werden. Die Lösungen können bis
zum jeweils angegebenen Termin im entsprechenden Briefkasten auf 25.13.O2 oder per EMail an [email protected] abgegeben werden. Die Abgaben werden korrigiert und
an dem Übungstermin zurückgegeben, wo die Aufgaben besprochen werden. Korrigiert
werden nur leserliche Abgaben, bei Abgaben per E-Mail nur solche im PDF Dateiformat.
Klausurzulassung:
Zur Klausur wird jeder zugelassen, der an maximal zwei Übungsterminen gefehlt hat oder
mindestens zwei Übungsaufgaben vorgerechnet und dabei erklärt hat.
Übungstermin
17.04.
24.04.
01.05.
08.05.
15.05.
22.05.
Abgabe bis
15.04. 12:00 Uhr
22.04. 12:00 Uhr
keine Abgabe
06.05 12:00 Uhr
13.05 12:00 Uhr
20.05 12:00 Uhr
29.05.
05.06.
12.06.
19.06.
26.06.
03.07.
keine Abgabe
03.06 12:00 Uhr
10.06 12:00 Uhr
keine Abgabe
24.06 12:00 Uhr
02.07 12:00 Uhr
Aufgaben
1
2,3
4-6
7-9
10
Kommentar
Es findet keine Übung statt
Aufgabe 6 ist eine alte Klausuraufgabe
Während der Übung sollen Lösungen
zu einigen der Aufgaben 11 bis 17 erarbeitet werden
Es findet keine Übung statt
15-18
19-21
Es findet keine Übung statt
22-24
25,26
Letzte Übung vor der Klausur. Überlegen Sie sich Fragen oder Themen, die
wiederholt werden sollen.
Aufgabe 1:
Geben Sie eine deterministische Turingmaschine (Q, Σ, δ, s) an, die zu einer gegebenen Zahl
n ∈ N in Binärdarstellung eins addiert, wenn
1. die Bits in aufsteigender Reihenfolge ihrer Wertigkeit von links nach rechts hinter
dem initialen Symbol stehen (Initialkonfiguration (s, ., 001) für n = 4).
2. die Bits in absteigender Reihenfolge ihrer Wertigkeit von links nach rechts hinter
dem initialen Symbol stehen (Initialkonfiguration (s, ., 100) für n = 4).
Aufgabe 2:
M
Definieren Sie die Relation 7−→ für deterministische k-Band-Turingmaschinen.
Aufgabe 3:
Seien M1 = (Q1 , Σ, δ1 , s1 ) und M2 = (Q2 , Σ, δ2 , s2 ) deterministische 1-BandTuringmaschinen. Geben Sie eine deterministische 2-Band-Turingmaschine M an, so dass
für alle x ∈ Σ∗ gilt: M (x) = yes genau dann wenn M1 (x) = yes oder M2 (x) = yes.
Aufgabe 4:
Sei Σ := {a, b, c} und L := {an bm cn | n, m ∈ N} ⊂ Σ∗ eine Sprache über dem Alphabet Σ.
1. Geben Sie eine deterministische 2-Band-Turingmaschine M an, die L in einer minimalen Anzahl an Schritten akzeptiert.
2. Geben Sie eine möglichst gute, obere Zeitschranke f : N0 → N0 für M an.
3. Gibt es eine deterministische 1-Band-Turingmaschine, die L mit der Zeitschranke f
akzeptiert? Begründen Sie Ihre Antwort.
Aufgabe 5:
Sei A ⊂ N die Menge aller natürlichen Zahlen, die keine Primzahlen sind. Beschreiben Sie
mögliche Arbeitsweisen einer
1. deterministischen
2. nichtdeterministischen
Turingmaschine, um A zu akzeptieren. Wo liegt der Vorteil des Nichtdeterminismus?
Aufgabe 6 (alte Klausuraufgabe):
Gegeben sei das Alphabet Σ := {0, 1, 2}. Definiere die Sprache L ⊂ Σ∗ durch
L := {u2v | u, v ∈ {0, 1}∗ ∧ u ist ein zusammenhängender Teilstring von v}.
Geben Sie eine nichtdeterministische Turingmaschine M an, die L akzeptiert. Erläutern
Sie kurz die Arbeitsweise von M .
Aufgabe 7:
Geben Sie eine nichtdeterministische 2-Band Turingmaschine M = (Q, Σ, ∆, s) an, die für
jede Eingabe x ∈ Σ∗ eine |x|-stellige Binärzahl auf das Ausgabeband schreibt und dann in
Zustand h hält.
Die geschriebene Binärzahl soll nichtdeterministisch “geraten” werden, es soll also für jede
mögliche, |x|-stellige Binärzahl n einen Berechnungspfad in M geben, bei dem n geschrieben
wird. Formal soll also Folgendes erfüllt sein:
∀x ∈ Σ∗
∀n ∈ {0, . . . , 2|x| − 1} :
M∗
(s, ., x, ., ) 7−→ (h, .x, , .n, )
Aufgabe 8:
Definiere für eine gegebene Sprache L ⊂ Σ∗ über dem Alphabet Σ die Komplementsprache
L := Σ∗ \ L.
1. Zeigen Sie: Für jede deterministische Komplexitätsklasse C gilt
L∈C
⇔
L∈C
2. Gilt die Äquivalenz aus 1. auch für nichtdeterministische Komplexitätsklassen?
Begründen Sie Ihre Antwort.
3. Sei Q ⊂ {−, 0, . . . , 9}∗ die Menge aller ganzen Zahlen in Dezimaldarstellung, die
Quadratzahlen sind. Was enthält dann Q?
Aufgabe 9:
Definieren Sie, äquivalent zur NP-Vollständigkeit, den Begriff der P-Vollständigkeit. Hierzu ist es notwendig Reduktionen auf logarithmischen Platz zu definieren. Erläutern Sie
ebenfalls, warum ≤p zu diesem Zweck unzureichend ist.
Aufgabe 10:
Sei A ein beliebiges, NP-vollständiges Problem. Zeigen Sie:
A∈P
⇒
P = NP
Aufgabe 11 (Teil einer alten Klausuraufgabe):
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
4-Omni-Sat
Gegeben:
Frage:
Eine Menge von Boolschen Variablen X und eine Menge C von Klauseln
über X, so dass
1. ∀c ∈ C
|c| = 4 und
2. ∃x ∈ X
∀c ∈ C
(x ∈ c
∨
x ∈ c).
Ist C erfüllbar?
Aufgabe 12:
Sei X eine Menge von Boolschen Variablen und C eine Menge von Klauseln über X. Der
Klausel-Variablen-Graph G(X,C) hat einen Knoten x für jede Variable x ∈ X und einen
Knoten c für jede Klausel c ∈ C. Es gibt eine Kante {x, c} zwischen einem Variabelknoten
x und Klauselknoten c genau dann wenn c das Literal x oder x enthält.
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Connected Sat
Gegeben:
Frage:
Eine Menge von Boolschen Variablen X und eine Menge von Klauseln C
über X, so dass G(X,C) zusammenhängend ist.
Ist C erfüllbar?
Aufgabe 13:
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Traveling Salesman Problem (TSP) / Rundreiseproblem
Gegeben:
Frage:
Ein vollständiger Graph Kn = (V, E) mit n Knoten (d.h. |V | = n und
E = {{u, v} | u, v ∈ V ∧ u 6= v}), eine Bewertung der Kanten c : E → R+
und eine maximale Rundreiselänge l ∈ R+ .
Gibt es einen Hamilton Kreis v1 , . . . , vn , so dass
c({vn , v1 }) +
n−1
X
c({vi , vi+1 })
≤l
?
i=1
Aufgabe 14:
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Set Cover / Mengenüberdeckungsproblem
Gegeben:
Frage:
Eine endliche Menge U , eine Familie von n Teilmengen
S := {Si | 1 ≤ i ≤ n ∧ Si ⊆ U } und eine natürliche Zahl
S k ∈ N.
Gibt es eine Teilmenge C ⊆ S mit |C| ≤ k und U = S∈C S?
Aufgabe 15:
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Exact Cover by 3-Sets (X3C)
Gegeben:
Frage:
Zahlen n, k ∈ N, eine Menge U mit |U | = 3 · k,
und eine Familie von n dreielementigen Teilmengen
S := {Si | 1 ≤ i ≤ n ∧ Si ⊆ U ∧ |Si | = 3}. S
Gibt es eine Teilmenge C ⊆ S mit |C| = k und U = S∈C S?
Aufgabe 16:
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Degree Constrained Spanning Tree (DCST)
Gegeben:
Frage:
Ein ungerichteter, zusammenhängender Graph G = (V, E) und eine Zahl
k ∈ N.
Gibt es einen Teilgraphen T = (V, ET ) von G, so dass T ein Baum ist und
jeder Knoten in T einen Knotengrad (=Anzahl der inzidenten Kanten)
von höchstens k hat?
Aufgabe 17:
Sei G = (V, E) ein ungerichteter Graph und U ⊆ V eine Teilmenge der Knoten. U ist eine
dominierende Menge für G genau dann, wenn
∀v ∈ V :
v∈U
∨
(∃u ∈ U : {u, v} ∈ E).
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Dominating Set (DS)
Gegeben: Ein ungerichteter Graph G = (V, E) und eine Zahl k ∈ N.
Frage:
Gibt es eine dominierende Menge U für G mit |U | ≤ k?
Aufgabe 18:
Seien L1 und L2 zwei Sprachen über einem Alphabet Σ mit L1 ⊂ L2 . Zeigen oder widerlegen
Sie folgende Aussagen:
1. Wenn L1 NP-schwer ist, dann ist auch L2 NP-schwer.
2. Wenn L2 NP-schwer ist, dann ist auch L1 NP-schwer.
3. Wenn L1 ∈ P , dann auch L2 ∈ P .
4. Wenn L2 ∈ P , dann auch L1 ∈ P .
Aufgabe 19:
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Hitting Set
Gegeben:
Frage:
Eine Menge U , eine Familie von Teilmengen S := {S | S ⊆ U } und eine
natürliche Zahl k ∈ N.
Gibt es eine Teilmenge C ⊆ U mit |C| ≤ k und ∀S ∈ S : S ∩ C 6= ∅?
Aufgabe 20:
Für eine natürliche Zahl k ∈ N sei das Entscheidungsproblem k-Colorability wie folgt
definiert:
k-Colorability
Gegeben: Ein ungerichteter Graph G = (V, E)
Frage:
Gibt es eine Abbildung c : V → {1, . . . , k}, so dass
∀{u, v} ∈ E : c(u) 6= c(v)?
Untersuchen Sie die Zeitkomplexität der Probleme 2-Colorability und 3-Colorability.
Was können Sie anhand dieser Erkenntnisse über das folgende Problem aussagen?
Chromatic Number
Gegeben: Ein ungerichteter Graph G = (V, E) und eine Zahl k ∈ N
Frage:
Gibt es eine Abbildung c : V → {1, . . . , k}, so dass
∀{u, v} ∈ E : c(u) 6= c(v)?
Aufgabe 21:
Für eine natürliche Zahl k ∈ N definieren wir die k-te Scheibe des Clique Problems als
das folgende Entscheidungsproblem:
k-Clique
Gegeben: Ein ungerichteter Graph G = (V, E)
Frage:
Enthält G einen vollständigen Teilgraphen mit mindestens k Knoten?
Untersuchen Sie die Zeitkomplexität von k-Clique für alle natürlichen Zahlen k.
Aufgabe 22 (alte Klausuraufgabe):
Es ist bekannt, dass das Problem Partition NP-vollständig ist.
Partition
Gegeben:
Frage:
Eine Menge M = {m1 , . . . , mk } mit k Objekten und eine Gewichtung
c : M → N.
Gibt
A ∪ B = M mit A ∩ B = ∅ und
P es eine Partition
P
c(m)
=
c(m)
?
m∈A
m∈B
Betrachten Sie einen pseudopolynomiellen
Algorithmus für Partition, der für i = 0, . . . , k
P
und j = 0, . . . , s mit s =
c(m)
einen
Wert w(i, j) ∈ {0, 1} berechnet, so dass
m∈M
w(i, j) = 1 genau dann, wenn es eine Teilmenge A ⊆ {m1 , . . . , mi } gibt mit
X
c(m) = j.
m∈A
Initialisiert werden die Werte w(0, 0) = 1 und w(0, j) = 0 für j = 1, . . . , s.
1. Beschreiben Sie das Berechnungsverfahren für w(i, j) mit i > 0.
2. Wie kann mit Hilfe der berechneten w(i, j) Werte die Antwort ermittelt werden?
Aufgabe 23:
Formulieren Sie die Optimierungsprobleme Minimum Vertex Cover und Maximum
Knapsack, indem Sie jeweils folgendes angeben:
1. Die Menge aller zulässigen Eingaben D,
2. die Menge aller Lösungen S(I) für eine Instanz I ∈ D und
3. eine Bewertungsfunktion f , die jedem s ∈ S(I) einen positiven Wert zuordnet.
Aufgabe 24:
Führen Sie den FIRST-FIT Algorithmus mit den folgenden Instanzen für das Optimierungsproblem Minimum Bin Packing durch und bestimmen Sie jeweils den Wert RF F (I).
(
1
, wenn i gerade
1. I = (U, g) mit U := {o1 , . . . , o16 } und g(oi ) := 18
, wenn i ungerade
2


0.15, wenn 1 ≤ i ≤ 6
2. I = (U, g) mit U := {o1 , . . . , o18 } und g(oi ) := 0.34, wenn 7 ≤ i ≤ 12


0.51, wenn 13 ≤ i ≤ 18
Aufgabe 25:
Zeigen Sie, dass das folgende Problem NP-vollständig ist.
Disjoint Sets
Gegeben:
Frage:
Eine endliche Menge U , eine Familie von Teilmengen S = {S | S ⊆ U }
und eine Zahl k ∈ N.
Gibt es eine Teilmenge C ⊆ S, so dass C mindestens k Mengen enthält,
die alle paarweise disjunkt sind?
Aufgabe 26:
Zeigen Sie: Wenn es einen polynomiellen Approximationsalgorithmus mit additivem Fehler
für das Problem Maximum Clique gibt, dann gilt P = N P .
Definition (Wiederholung):
Sei X = {x1 , . . . , xn } eine Menge Boolescher Variablen.
Eine Belegung für X ist eine Abbildung t : X → {T, F }.
Für eine Variable x ∈ X sei x das positive und x das negative Literal.
Das Literal x ist wahr unter t, falls t(x) = T , das Literal x ist wahr, falls t(x) = F .
Eine Klausel C über X ist eine Menge von Literalen über X.
Klausel C wird von einer Belegung t für X erfüllt, wenn C mindestens ein Literal enthält,
das unter t wahr ist. Eine Menge F von Klauseln über X ist erfüllbar, wenn es eine Belegung
t für X gibt, die jede Klausel erfüllt.
Aufgabe ??:
Zeigen Sie, dass folgende Probleme in P liegen, d.h. geben Sie deterministische Algorithmen
an, die die Probleme in polynomieller Zeit entscheiden. Die formale Angabe von Turingmaschinen ist nicht notwendig.
HORN-SAT
Gegeben:
Frage:
Eine Menge Boolscher Variablen X und eine Menge F von Klauseln über
X, so dass jede Klausel höchstens ein positives Literal enthält.
Ist F erfüllbar?
2-SAT
Gegeben:
Frage:
Eine Menge Boolscher Variablen X und eine Menge F von Klauseln über
X, so dass jede Klausel genau zwei Literale enthält.
Ist F erfüllbar?