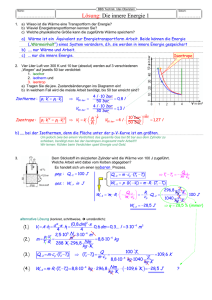
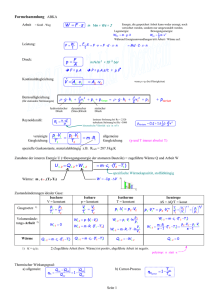
U m c T T

BBS Technik Idar-Oberstein
Name:
Thermodynamik III:
Datum:
Innere Energie
Um den Zustand eines Gases zu ändern, muss ein Energietransport (über die Systemgrenzen hinein oder heraus)
stattfinden. Dies kann nur durch die Energietransport formen Arbeit und/oder Wärme geschehen.
(Wärme und Arbeit sind also keine Zustands-, sondern Prozessgrößen.)
z.B. bei konstantem Druck
bei beliebigem Druckverlauf
a) Die Wärme Q ist eine Energieform, die allein auf Grund
von unterschiedlichen Temperaturen übertragen wird.
b) Die Arbeit W (=Kraft ⋅ Weg) geschieht durch die Volumenänderung des Gases mittels Kraftanwendung.
Die Zuführung von Arbeit oder/und Wärme in ein abgeschlossenes Gas erhöht die Energie des Systems.
Minus-Zeichen kennzeichnet die Richtung:
Arbeit geht hinaus (-) oder hinein (+)
Die zugeführten Energien können also einzig und allein nur als Bewegungsenergie der Moleküle gespeichert sein. Diese
Speicherform der Energie nennt man
U1−2 = Q1−2 +W1−2
innere Energie
in J
Die innere Energie U ist die Energie, die ein Stoff auf Grund seiner
Molekularbewegungen hat. Sie äußert sich nach außen über die Temperatur.
Sie ist eine Zustandsgröße.
Am einfachsten berechnet man die innere Energie eines bestimmten
Zustandes mit der Wärmemenge, die man zur isochoren Änderung benötigt.
(denn dann ist keine Arbeit mit im Spiel; U1−2 = m ⋅ cv ⋅ (T2 −T1 )
gilt allgemein!
Energieaustausch bei den jew. Sonderfällen:
a) Isochore
Beim Überführen des Gases vom Zustand 1
nach Zustand 2 wird keine Arbeit verrichtet.
∆U = Q1-2 + W 1-2 Somit kommt es zu einer
vollständigen Umwandlung von Wärme in
innere Energie. ∆U = Q1-2
W 1-2 = 0
Q1-2 = m⋅cv⋅T2-T1)
b) Isobare
Die Arbeit W 1-2 = -p⋅∆V = p⋅ (V1-V2); Sie ist
laut Definition negativ, wenn das Gas
expandiert und somit Arbeit abgeführt wird.
p⋅V1 ist laut Gasgesetz m⋅Ri⋅T1 ; also kann
man die Arbeit auch aus m⋅Ri⋅ (T1-T2) berechnen.
W 1-2 = p⋅ (V1-V2)
W 1-2 = m⋅Ri⋅ (T1-T2)
Q1-2 = m⋅cp⋅ (T2-T1)
c) Isotherme
Die (Volumenänderungs-)Arbeit ist hier
schwieriger zu bestimmen, da sich die Kraft
längs des Weges ändert. Die Arbeit ist die
Summe aller Flächenelemente unter der p-VLinie: Die durch die Verdichtungsarbeit W 1-2
zugeführte Energie, muss, damit U und T
nicht ansteigen, sofort wieder in Form von Wärme abgeführt
werden!!!
∆U = Q1-2 + W 1-2 .= 0 Q1-2 = -W 1-2 .
d) Isentrope (keine Wärme kann fließen)
Wenn beim Verdichten keine Wärme
abgeführt wird, so steigt die innere Energie
und somit die Temperatur an. Deshalb
verläuft (laut Gasgleichung) die Zustandslinie
im p-V-Diagramm steiler als die der Isothermen.
Wenn Q=0, dann folgt aus der allg. Gleichung
∆U = W1-2 = m⋅cv⋅ (T2-T1).
∆U = Q1-2 + W 1-2
W 1-2 = p1⋅V1⋅ ln(V1/V2)
W 1-2 = m⋅Ri⋅T ⋅ ln(V1/V2)
ohne Herleitung:
Q1-2 = -W 1-2
κ=cp/cv
Isentropenexponent
W 1-2 = m⋅cv⋅ (T2-T1)
e) allgemeinster Fall: Meistens tritt dennoch etwas Wärme auf; statt κ verwendet man dann n
Q1-2 = 0
Polytropen exponent
BBS Technik Idar-Oberstein
Name:
Datum:
Innere Energie
Thermodynamik III:
1. a) Wieso ist die Wärme eine Transportform der Energie?
b) Wie viel Energietransportformen kennen Sie?
c) Welche physikalische Größe kann die zugeführte Wärme speichern?
a) Wärme ist ein Äquivalent zur Energietransportform Arbeit. Beide können die Energie
(„Wärmeinhalt“) eines System verändern, d.h. sie werden in innere Energie gespeichert
b) .... nur Wärme und Arbeit.
c) ... nur die innere Energie.
Isentrope
2. Vier Liter Luft von 300 K und 10 bar (absolut) werden auf 3 verschiedenen
„Wegen“ auf jeweils 50 bar verdichtet:
1. isochor
2. isotherm und
3. isentrop
a) Tragen Sie die jew. Zustandsänderungen ins Diagramm ein!
b) In welchem Fall wird die meiste Arbeit benötigt, bis 50 bar erreicht sind?
⇒ V50 bar =
Isotherme : p1 ⋅V1 = p2 ⋅V2
V30 bar =
4 l ⋅ 10 bar
= 0, 8 l
50 bar
4 l ⋅ 10 bar
= 1,3 l
30 bar
1
1
Isentrope :
κ
κ
p1 ⋅V1 = p2 ⋅V2
p κ
⇒ V2 = V1 ⋅  1 
 p2 
V50 bar
 10 bar  1402,
=4 l ⋅
= 1,27 l

 50 bar 
b) .... bei der Isothermen, denn die Fläche unter der p-V-Kurve ist am größten.
Um jedoch (wie bei einem Verdichter) das gesamte Gas bei 50 bar aus dem Zylinder zu
schieben, benötigt man bei der Isentropen insgesamt mehr Arbeit!!!
Wir lernen: Kühlen beim Verdichten spart Energie und Geld.
3.
Dem Stickstoff im skizzierten Zylinder wird die Wärme von 100 J zugeführt.
Welche Arbeit wird dabei vom Kolben abgegeben?
Es handelt sich um einen isobaren Prozess.
geg . : Q1−2 = 100 J
Q1−2 = m ⋅ cp ⋅ (T2 −T1)
ges . : W1−2 in J
W1−2 = p ⋅ (V1 −V2) = m ⋅ Ri ⋅ (T1 −T2)
W1 −2
⇒T1 −T2 = −
Q1−2
m ⋅ cp
296,8 J
kg ⋅ K
 Q1−2 
Ri
= m ⋅ Ri ⋅  −
= − ⋅ Q1−2 = −
⋅ 100 J

m
c
⋅
c
p
p 

1040 J
kg ⋅ K
W1−2 = −28,5 J
⇒ η = 28,5 % (immer )
alternative Lösung (konkret, schrittweise, umständlich):
2
1.
2.
3.
4.
2
(0,8dm) ⋅π
V1 = A ⋅h1 = d ⋅π ⋅h1 =
⋅ 0,6dm = 0,3... l = 3⋅10 −4 m 3
4
4
5 N
−4
3
p1 ⋅V1 2,5 ⋅10 m 2 ⋅3⋅10 m
=
= 8,8 ⋅10 −4 kg
m=
T1 ⋅Ri 288 K ⋅296,8 Nm
kg ⋅ K
100 J
Q
Q1−2 = m ⋅cp ⋅(T2 −T1) ⇒ (T2 −T1) = m ⋅c =
= 109,6 K
p
8,8 ⋅10 −4 kg ⋅1040 J
kg ⋅K
−4
Nm
⋅ ( −109,6 K ) = −28,5 J
W1−2 = m ⋅Ri ⋅(T1 −T2) = 8,8⋅10 kg ⋅ 296,8
kg ⋅ K
immer ?
BBS Technik Idar-Oberstein
Name:
Datum:
Innere Energie
Thermodynamik III:
4. Streichen Sie die falschen Aussagen durch (u. kreuzen Sie die richtigen an)!
Das allgemeine Gasgesetz gilt nur für ideale Gase.
Zwischen den Molekülen des idealen Gases wirken keine Kraftfelder.
Wärme ist eine von vielen Speicherformen der Energie.
Innere Energie kann je nach Prozess in Wärme oder Arbeit abgeführt werden.
Eine isotherme Expansion ist nur möglich, wenn das System 100%-ig wärmeisoliert ist.
In einem eingeschlossenen Gas kann die zugeführte Energie einzig und allein nur in innerer Energie vorliegen.
5. Füllen Sie die Tabelle aus!
(ankreuzen und p-V-Diagramm zeichnen)
6. Warum ist eine Verdichtung nur dann isotherm, wenn sie entweder nur sehr langsam abläuft oder gekühlt wird?
Durch die Kompression wird Arbeit (=-Σp⋅∆V) verrichtet. Diese würde die innere Energie (~T) des
Systems erhöhen, wenn nicht gleichzeitig die gesamte zugeführte Arbeit als Wärme sofort wieder
abgeführt würde (W=-Q)
7. Wie kann man den (für Physik und Technik sehr bedeutsamen) Energieerhaltungssatz math. knapp formulieren?
U1−2 =Q1−2 +W1−2
That’s all.
8. Der rechts skizzierte Kompressor erzeugt im Druckbehälter von 24 Liter einen
Druck von 8 bar.
a) Wie hoch wäre die Temperatur der verdichteten Luft im Kompressor, wenn
keine Kühlung stattfinden würde? (Reibung vernachlässigbar)
8 bar
278 oC
b) Skizzieren Sie die beiden Verdichtungsprozesse in ein p-V-Diagramm ein!
geg . : p1 = 1 bar
p2 = 9 bar
T1 = 293 K
ges . : T2 in K
b)
T1  p1 
=
T2  p2 
κ −1
κ
κ −1
p κ
⇒T2 =T1 ⋅  2  = 293 K ⋅ 9
 p1 
= 551 K = 278 oC
0,402
1,4
=
größere Verdichtungsarbeit, störende Temperatur,
im Kessel: Druckabfall durch Abkühlung
9. Leo bedient den Presslufthammer seiner Teerstraßenausbesserungsbrigade ganz virtuos. Er kann sich aber bis
heute nicht erklären, warum die zum Antrieb benötigte Pressluft so kalt aus dem Auspuff entweicht (an manchen
Tagen vereist er sogar), wo doch die Temperatur im Druckluftkessel etwa 20 oC beträgt. Erklären Sie’s ihm!
Die im Druckkessel gespeicherte Energie liegt nur als innere Energie vor. Verrichtet das Gas nun
Arbeit, fällt die innere Energie (∆U = m⋅cv⋅∆T) und somit die Temperatur.