GM3 SB LOES.indd - Bildungsverlag Lemberger

1
1 Mein Wissen aus der 2. Klasse
1
▶ Olympiade nennt man den Zeitraum zwischen zwei Olympischen Spielen, den Zeitraum der Spiele zu Beginn
der Olympiade mit eingeschlossen.
▶ 90 Service wurden trainiert.
▶ Sommerspiele: 1960, Rom, Italien
Winterspiele: 1976, Örnsköldsvik, Schweden
Klammerrechnung vor Punktrechnung vor Strichrechnung
2
a) 0,8 • 2 = 1,6
3
a) 1, 2, 4, 5, 10, 20
c) 1, 2, 3, 6, 9, 18
4
a)
b) 4,1 • 0,3 = 1,23
b) 1, 2, 3, 4, 6, 9, 12, 18, 36
d) 1, 2, 4, 5, 10, 20, 25, 50, 100
24 2
60
12 2
30
6 2
15
3 3
5
1
1
ggT(24, 60) = 2 • 2 • 3 = 12
c)
12 2
6 2
3 3
1
c) 3,2 + 4,83 = 8,03
b)
2
2
3
5
30 2
15 3
5 5
1
d)
5
45, 54, 63, …
6
a)
8 2
10 2
4 2
5 5
2 2
1
1
kgV(8, 10) = 2 • 5 • 2 • 2 = 40
b)
c)
8 2
14 2
4 2
7 7
2 2
1
1
kgV(8, 14) = 2 • 7 • 2 • 2 = 56
d)
a)
•2
27 3
9 3
3 3
1
54
27
9
3
1
ggT(27, 54) = 3 • 3 • 3 = 27
6 2
3 3
1
8 2
4 2
2 2
1
kgV(6, 8) = 2 • 2 • 2 • 3 = 24
5 5
1
c)
__
​ 46 ​ = __
​ 69 ​
​  23 ​ = __
•2
•3
•3
•3
a) __
​  23 ​
b) __
​  13 ​
c) __
​  78 ​
d) __
​  12 ​
e) 2
9
a) 0,05
b) 0,27
c) 0,5
d) 0,75
40
  ​  =
e) ___
​  100
1
1
6
3
9
​ 79 ​ = __
​ 15
  ​ = 1 __
​ 69 ​ = 1 __
​ 23 ​ c) ​ __
  ​ – __
​ 10
  ​ = __
​ 10
  ​
a) ​ __89 ​ + __
9
10
e) ​ __4 ​ • __
​ 3 ​ = __
​ 1 ​
93 8 2 6
b) __
​  23 ​ + __
​ 23 ​ = __
​ 43 ​ = 1 __
​ 13 ​
3
f) __
​  25 ​ • __
​ 34 ​ = __
​ 10
  ​
2
14
GM3 SB LOES.indd 14
7 7
1
9
__
​ 68 ​ = __
​ 12
  ​
​ 34 ​ = __
•2
8
10
2
3
3
3
kgV(5, 7) = 5 • 7 = 35
b)
•3
​ __12 ​ = __
​ 24 ​ = __
​ 36 ​
•2
21 3
7 7
1
ggT(14, 21) = 7
ggT(12, 30) = 2 • 3 = 6
7
14 2
7 7
1
d) 1 ​ __23 ​ – __
​ 13 ​ = 1 __
​ 13 ​
1
7
f) __
​  10
  ​
__
​ 25 ​
25
f) ​ ___
  ​  =
100
__
​ 14 ​
1
2
8
g) __
​  54 ​ • __
​ 10
  ​ = __
​ 22 ​ = 1
2
1
2
1
​  37 ​ • __
​ 14
  ​ = __
​ 22 ​ = 1
h) __
6
1
2
Genial! Mathematik 3 – Lösungen
19.07.12 11:02
1
1 Mein Wissen aus der 2. Klasse
11
a)
b)
b6
c 3
c 5
f 2
g7
y
6
5
4
3
2
1
0
C
D
A
B
1 2 3 4 5 6
12
0° < α < 90° spitzer W.
β = 90° rechter W.
13
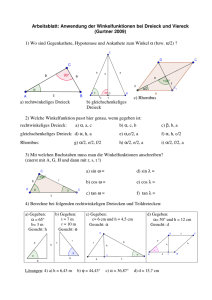
Nach den Seitenlängen: gleichseitig, gleichschenkelig, ungleichseitig
Nach den Winkelarten: stumpfwinkelig, rechtwinkelig, spitzwinkelig
14
Gleichseitiges Dreieck: a = b = c; α = β = γ = 60°; u = 3 • a
Gleichschenkeliges Dreieck: a = b; α = β; u = 2 • a + c
Rechtwinkeliges Dreieck: ein rechter Winkel
Stumpfwinkeliges Dreieck: ein stumpfer Winkel
15
a) ungleichseitiges rechtwinkeliges Dreieck
a = 6 cm; b = 10 cm; c = 8 cm
10
9
8
7
6
5
4
3
2
1
90° < γ < 180° stumpfer W.
δ = 180° gestreckter W.
y
b
a
B
c
A
x
1 2 3 4 5 6 7 8 9 10
0
10
9
8
7
6
5
4
3
2
1
0
16
y
C
b
A
a
c
B
x
1 2 3 4 5 6 7 8 9 10
y
B
a
C
c
b
x
A
1 2 3 4 5 6 7 8 9 10
0
c) gleichschenkeliges spitzwinkeliges Dreieck
a ≈ 7,6 cm; b ≈ 7,6 cm; c = 6 cm
180° < ε < 360° erhabener W.
ρ = 360° voller W.
b) gleichschenkeliges stumpfwinkeliges Dreieck
a ≈ 5,8 cm; b ≈ 5,8 cm; c = 10 cm
10
9
8
7
6
5
4
3
2
1
C
x
d) ungleichseitiges rechtwinkeliges Dreieck
a ≈ 9,2 cm; b = 6 cm; c = 7 cm
10
9
8
7
6
5
4
3
2
1
0
y
C
a
b
A
c
B x
1 2 3 4 5 6 7 8 9 10
H Höhenschnittpunkt: Schnittpunkt der Seitenhöhen
U Umkreismittelpunkt: Schnittpunkt der Seitensymmetralen
I Inkreismittelpunkt: Schnittpunkt der Winkelsymmetralen
S Schwerpunkt: Schnittpunkt der Schwerlinien
Genial! Mathematik 3 – Lösungen
GM3 SB LOES.indd 15
15
19.07.12 11:02
1
17
1 Mein Wissen aus der 2. Klasse
a)
b)
Äpfel (kg)
1
2
3
10
__
​  12 ​
Preis (€)
2
4
6
20
1
18
Quader
Würfel
0,5
Arbeiter
5
1
3
9
15
Zeit (Tage)
9
45
15
5
3
Ecken Kanten Flächen Grundriss
Formel
8
12
6
Rechteck G = a • b
8
12
6
Quadrat G = a • a
Prisma
19
__
​  14 ​
6
9
a•b
⊿ Dreieck G = ​ ____
   ​ 
2
5
Formel
O = 2(a • b + b • h + a • h)
O=6•a•a
a•b
O = a • b + a • h + b • h + c • h V = ​ ____
   ​ • h
2
W • 100
 
​
G = ​ ______
p   
a) G: Grundwert
G•p
W = ​ ____
  ​
100
b) W: Prozentwert
​ 100G•  W 
p = ______
​
 
c) p: Prozentsatz
20
120 Kinder besuchten die beiden Klassen.
21
a) Tennis (40 %)
b) Tennis: 10; Handball: 8; Fußball: 7
c) Tennis: 40 %; Handball: 32 %; Fußball: 28 %
40 %
32 %
40 %
≙ 144 °
32 %
≙ 115,2 °
a) 38 604
36 607
23
mehrere Lösungsmöglichkeiten!
a) x = 1,55; 5; 11
b) x = 1; 2; 3; 4; 6; 12; 18; 24; 36; 72 c) 9; 18; 27; …
25
28 %
≙ 100.8 °
28 %
22
24
Formel
V=a•b•h
V=a•a•a
b) 90 210
90 510
c) 2 103
2 704
d) 9 849
9 879
d) 5; 10; 15; …
Primzahlen sind natürliche Zahlen größer als 1, welche nur durch 1 und sich selbst ohne Rest teilbar sind.
2, 3, 5, 7, 11, 13, 17, 19, 23, 29
a+b
a–c
a+b+c
a–b–c
a•b•c
7
5 ​ __
  ​
10
4 __
​  12 ​
5 __
​  45 ​
3 __
​  25 ​
___
​  253
  ​
500
26
Individuelle Lösung
27
supplementäre Winkel
28
α
29
a) α = 73°
30
H, U, S liegen auf einer gemeinsamen Geraden
31
(7 – b)
​ 
​  4   
a) b = 7 – 4a; a = _____
16
GM3 SB LOES.indd 16
b) β = 54°
c) α = 24°
a) α ≈ 31°; γ ≈ 83°
(8 – 2y)
b) x = ​ ______
   
 ​ = 4 – y;
2
b) α ≈ 62°
(8 – 2x)
y = ______
​  2   
​ = 4 – x
Genial! Mathematik 3 – Lösungen
19.07.12 11:02
1 Mein Wissen aus der 2. Klasse
32
a) 18 km
b) 45 km
33
a) u = a + b + c + d
u–a–b–c=d
d = 8,1 m
b) d = u – a – b – c
d = 6,1 cm
34
a) G = 54 m2
b) V = 2 700 m3
35
2 … die letzte Stelle der Zahl muss 0, 2, 4, 6 oder 8 sein.
3 … die Ziffernsumme muss durch 3 teilbar sein.
5 … die letzte Stelle muss 0 oder 5 sein.
9 … die Ziffernsumme muss durch 9 teilbar sein.
10… die letzte Stelle muss 0 sein.
4 … die aus den beiden letzten Ziffern gebildete Zahl muss durch 4 teilbar sein.
25… die aus den beiden letzten Ziffern gebildete Zahl muss durch 25 teilbar sein.
36
Der ggT ist das Produkt der gemeinsamen Primfaktoren der Zahlen, daher werden jene Primfaktoren
multipliziert, die sowohl in der einen als auch in der anderen Zahl vorkommen.
Das kgV ist die kleinste Zahl, in der die gegebenen Zahlen enthalten sind. Es werden die Primfaktoren
der größeren Zahl mit den noch nicht ausgewählten Primfaktoren der anderen Zahl multipliziert.
37
a)
38
individuelle Lösung
39
a) α = 180‘
40
Der Inkreismittelpunkt liegt nur im gleichschenkeligen Dreieck auf der Euler‘schen Geraden.
Im gleichseitigen Dreieck fallen H, U, S und I in einen Punkt zusammen, es gibt hier keine Euler‘sche
Gerade.
41
r ≈ 1 cm
42
{21, 22, 23, …, 45, 46, 47}
43
a) a = 3;
44
a) 2,4 h
45
   
 
​
A = y • y + ​ _______
2
46
a) h = 5 m
47
absolute Häufigkeit: 730;
48
Individuelle Lösung: z. B. Veränderung der Einheiten auf den Achsen, …
__
 ​
​ 17
32
c) 22,5 km d) 4,5 km
e) 2,25 km
1
b) 2 __
​ 15
  ​
1
c) 1 __
​ 20
  ​
b) β = 1 803‘
c) γ = 402‘
b) x = 3;
Probe: 32
Probe: 68
b) s = 100 km
(x – y) • y
oder
(x + y) • y
A = _______
​  2   
​ 
b) G = 25 dm2; V = 125 dm3
relative Häufigkeit: 0,73
Genial! Mathematik 3 – Lösungen
GM3 SB LOES.indd 17
1
17
19.07.12 11:02