Übungen zu Frage 78 - Mathematik

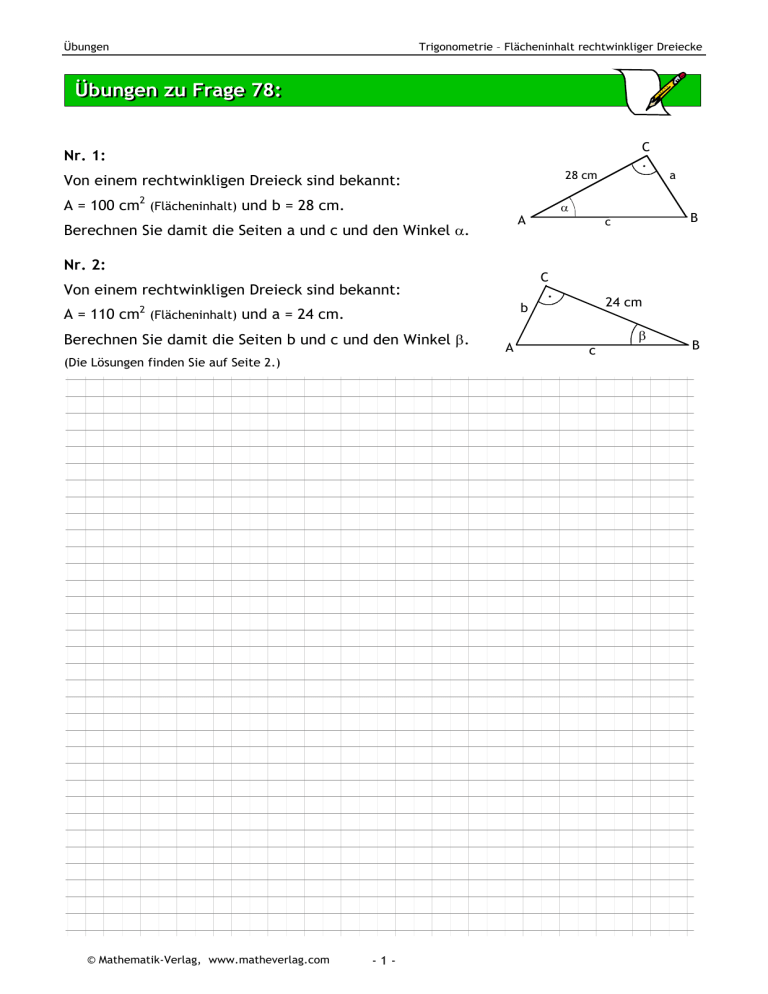
Übungen
Trigonometrie – Flächeninhalt rechtwinkliger Dreiecke
Übungen zu Frage 78:
C
Nr. 1:
28 cm
Von einem rechtwinkligen Dreieck sind bekannt:
A = 100 cm2 (Flächeninhalt) und b = 28 cm.
Nr. 2:
.
24 cm
b
2
A = 110 cm (Flächeninhalt) und a = 24 cm.
Berechnen Sie damit die Seiten b und c und den Winkel β.
(Die Lösungen finden Sie auf Seite 2.)
-1-
B
c
C
Von einem rechtwinkligen Dreieck sind bekannt:
© Mathematik-Verlag, www.matheverlag.com
α
A
Berechnen Sie damit die Seiten a und c und den Winkel α.
a
A
β
c
B
Lösungen:
C
Nr. 1:
a ⋅b
2
ergibt: 100 =
a ⋅ 28
2
⇔ a = 7,14 cm
m
4c
A=
7,1
28 cm
Einsetzen von A = 100 cm2 und b = 28 cm in die Formel
α
A
B
c
Mit dem Satz des Pythagoras erhält man:
c2 = 28 2 + 7,14 2 = 834,98 ⇔ c = 28,90 cm
Der Winkel α kann beispielsweise mit der Tangensfunktion
berechnet werden. Es gilt:
tan α =
7,14
28
⇒ α = 14,3°
Nr. 2:
Einsetzen von A = 110 cm und a = 24 cm in die Formel
A=
a ⋅b
2
ergibt: 110 =
24 ⋅ b
2
⇔ b = 9,17 cm
A
Mit dem Satz des Pythagoras erhält man:
c2 = 24 2 + 9,17 2 = 660,09 ⇔ c = 25,7 cm
Der Winkel β kann beispielsweise mit der Tangensfunktion
berechnet werden. Es gilt:
tan β =
9,17
24
⇒ β = 20,9°
© Mathematik-Verlag, www.matheverlag.com
9,1
7c
m
C
2
-2-
.
24 cm
β
c
B