Multiplikation
Werbung

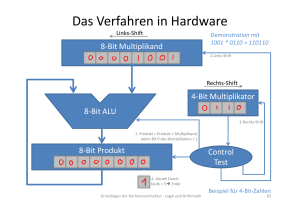
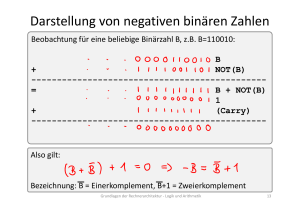
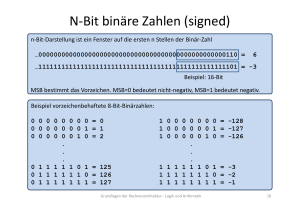
Multiplikation Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 79 Multiplikation nach der Schulmethode Gegeben seien die Binärzahlen A und B. Was ist a * b? Beispiel: Multiplikand A: Multiplikator B: 1 1 0 1 0 * 1 1 0 1 ----------- Produkt: Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 80 Maximale Länge des Ergebnisses Beobachtung: Multiplikand der Länge n Bits und Multiplikator der Länge m Bits ergibt Produkt einer Länge mit maximal n+m Bits. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 81 Das Verfahren als Algorithmus Start Beispiel 1001*0101: Teste erstes Multiplikator ‐Bit 1 0 Addiere Multiplikand zum Produkt Shifte Multiplikand ein Bit nach Links Shifte Multiplikator ein Bit nach Rechts 5ter Durch‐ lauf? Beispiel für 4‐Bit‐Zahlen ja Ende nein 1 0 0 1 * 0 1 0 1 ---------1 0 0 1 + 0 0 0 0 -----------1 0 0 1 + 1 0 0 1 -------------1 0 1 1 0 1 + 0 0 0 0 ---------------0 1 0 1 1 0 1 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 82 Das Verfahren in Hardware Links‐Shift Demonstration mit 1001 * 0110 = 110110 8‐Bit Multiplikand 2.Links‐Shift Rechts‐Shift 4‐Bit Multiplikator 8‐Bit ALU 3.Rechts‐Shift 1. Produkt = Produkt + Multiplikand, wenn Bit 0 des Multiplikators = 1 8‐Bit Produkt Control Test 4. Anzahl Durch‐ läufe = 5 Ende Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik Beispiel für 4‐Bit‐Zahlen 83 Vorzeichenbehaftete Multiplikation ‐ Betrachte Multiplikand x und Multiplikator y. ‐ Sei x‘ = x wenn x nicht‐negativ bzw. x‘ = ‐x sonst. ‐ Sei y‘ = y wenn y nicht‐negativ bzw. y‘ = ‐y sonst. ‐ Berechne z‘ = x‘ * y‘. ‐ Ergebnis z = z‘ wenn x und y nicht‐negativ oder x und y negativ, ansonsten ist z = ‐z‘. • Möglichkeit 2: Tausche im Verfahren der vorigen Folie das Produkt‐ register mit einem vor‐ zeichenbehafteten Rechts‐ Shift‐Register aus. Bildquelle: David A. Patterson und John L. Hennessy, „Computer Organization and Design“, Fourth Edition, 2012 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 84 Weitere Beschleunigungen Eine ALU für jede Summation x3*y x2*y x1*y x0*y3y2y1 x0*y0 4‐Bit‐ALU c s3 s2 s1 s0 4‐Bit‐ALU c s3 s2 s1 s0 4‐Bit‐ALU c s3 s2 s1 s0 z7z6z5z4z3 Beispiel für 4‐Bit‐Zahlen z2 z1 Beobachtung: 1 0 1 1 (Y) * 1 1 1 0 (X) ---------------0 0 0 0 + 1 0 1 1 -------------= 1 0 1 1 + 1 0 1 1 -----------= 1 0 0 0 0 + 1 0 1 1 ---------------=1 0 0 1 1 0 1 0 (Z) z0 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 85 Weitere Beschleunigungen Parallele Organisation der ALUs in einen Binärbaum (keine weiteren Details hier) Jede ALU‐Operation verbrauche einen Taktzyklus. Wie viele Taktzyklen dauert die Multiplikation von 32‐Bit‐Zahlen? Bildquelle: David A. Patterson und John L. Hennessy, „Computer Organization and Design“, Fourth Edition, 2012 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 86 Division Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 87 Division nach der Schulmethode Gegeben seien die Binärzahlen A und B. Was ist a : b? Beispiel: Dividend Divisor Quotient 1 0 0 1 0 1 0 : 1 0 0 0 = Rest: Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 88 Das Verfahren als Algorithmus Start Beispiel 1001 : 10: Subtrahiere Divisor vom Rest ≥0 Teste Rest <0 Restauriere den alten Rest. Shifte Quotient nach Links und setze dessen LSB=0. Shifte Quotient nach Links und setze dessen LSB=1. Shifte Divisor ein Bit nach Rechts Beispiel für 4‐Bit‐Zahlen 6ter Durch‐ lauf? ja Ende nein Dvdt :Dvsr= Qtnt 001001 : 10 = 00100 -000000 100000 -----01001 -00000 10000 ----1001 -1000 1000 ---001 -000 100 --01 -00 10 -1 Rest Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 89 Das Verfahren in Hardware Rechts‐Shift Demonstration mit 1001 : 0010 = 100 Rest 1 8‐Bit Divisor 3. Rechts‐Shift Links‐Shift 4‐Bit Quotient 8‐Bit ALU 2. Links‐Shift; LSB=Rest wurde verändert 4. Anzahl Durch‐ läufe = 6 Ende 1. Rest=Rest‐Divisor, wenn Divisor < Rest 8‐Bit Rest Control Test Beispiel für 4‐Bit‐Zahlen Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 90 Vorzeichenbehaftete Division • Umgang mit dem Quotienten (analog wie für Multiplikation): ‐ Betrachte Divisor x und Dividend y (also: Quotient z von y:x). ‐ Sei x‘ = x wenn x nicht‐negativ bzw. x‘ = ‐x sonst. ‐ Sei y‘ = y wenn y nicht‐negativ bzw. y‘ = ‐y sonst. ‐ Berechne Quotient z‘ von y‘ : x‘. ‐ Ergebnis z = z‘ wenn x und y nicht‐negativ oder x und y negativ, ansonsten ist z = ‐z‘. • Und was ist das Vorzeichen des Rests? Beispiel: Dividend : Divisor Quotient Rest Quotient * Divisor + Rest = Dividend 7 : 2 3 1 3 * 2 + 1 = 7 -7 : 2 -3 -1 -3 * 2 – 1 = -7 7 : -2 -3 1 -3 * -2 + 1 = -7 : -2 3 -1 3 * -2 – 1 = -7 7 •Also: Vorzeichen des Rests ist Vorzeichen des Dividend. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 91 Gleitkommazahlen Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 92 Reelle Gleitkommazahlen Kleine Zahl Große Zahl Beispiel Wissenschaftliche Darstellung (eine Ziffer links des Kommas) Normalisierte Darstellung (keine führende Null) Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 93 Binäre Gleitkommazahlen Was ist der Dezimalwert der binären Gleitkommazahl 101,1001? Was bedeutet 11,011 * 22? Also: mit 2i multiplizieren verschiebt das Komma um i Stellen nach rechts. Analog: mit 2‐i multiplizieren verschiebt das Komma um i Stellen nach links. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 94 Binäre Gleitkommazahlen Was ist die wissenschaftliche, normalisierte Darstellung der binären Gleitkommazahl zur dezimalen Gleitkommazahl 0,625? Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 95 Nebenbemerkung Betrachte die recht harmlose Dezimalzahl 0,8. Für die folgende unendliche Reihe rechnet man leicht nach: (2‐1 + 2‐2) + (2‐5 + 2‐6) + (2‐9 + 2‐10) + (2‐13 + 2‐14) + ... = 4/5 = 0.8 Folglich ist die Binärdarstellung von 0.8 unendlich lang, nämlich: 0 , 1100 1100 1100 1100 1100 1100 1100 ... Annahme wir speichern nur die ersten 32 Bits. Rechnet man in den Dezimalwert x zurück, dann ergibt sich: x = (2‐1 + 2‐2) + (2‐5 + 2‐6) + (2‐9 + 2‐10) + ... + (2‐29 + 2‐30) = 858.993.459 / 1.073.741.824 = 0,79999999981373548508 ≠ 0,8 Oha, 0,8 ist scheinbar doch nicht so harmlos. Es gibt folglich Zahlen mit endlicher dezimaler Gleitkommadarstellung, die binär nicht mit endlicher Anzahl Bits darstellbar sind. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 96 N‐Bit Darstellung von Gleitkommazahlen Normalisierte, wissenschaftliche Darstellung zur Basis 2. Beispiel: Allgemein: Sign‐and‐Magnitude‐Darstellung für beispielsweise 32 Bits: (s=0 für „+“ und s=1 für „‐“) s exponent fraction 1 Bit 8 Bits 23 Bits Tradeoff: Viele Fraction‐Bits: hohe Genauigkeit der Fraction Viele Exponent‐Bits: großer darstellbarer Zahlenbereich Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 97 Beispiel s exponent fraction 1 Bit 8 Bits 23 Bits Was ist der Dezimalwert x des folgenden Bit‐Strings? 10000010110110000000000000000000 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 98 Wertebereiche, Overflow und Underflow s exponent fraction 1 Bit 8 Bits 23 Bits Kleinste darstellbare nicht‐negative Zahl annähernd 2,0 * 10‐38 Größte darstellbare Zahl annähernd 2,0 * 1038 Was, wenn die darzustellende Zahl außerhalb dieses Bereichs ist? Overflow: Zahl zu groß (Exponent ist zu groß um im Exponent‐Feld darstellbar zu sein) Underflow: Zahl zu klein (Negativer Exponent ist zu groß um im Exponent‐Feld darstellbar zu sein) Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 99 Double‐ und Single‐Precision Beispiel: Single‐ Precision Double‐ Precision Insgesamt 32 Bits s exponent 1 Bit 8 Bits fraction 23 Bits Insgesamt 64 Bits s exponent 1 Bit 11 Bits fraction 52 Bits Double‐Precision hat höhere Genauigkeit der Fraction und mit größerem Exponent auch einen größeren darstellbaren Zahlenbereich. Double‐Precision in diesem Beispiel: Kleinste darstellbare nicht‐negative Zahl annähernd 2,0 * 10‐308 Größte darstellbare Zahl annähernd 2,0 * 10308 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 100 Der Zahlenformatstandard IEEE 754 Single‐ Precision Double‐ Precision Insgesamt 32 Bits s exponent 1 Bit 8 Bits fraction 23 Bits Insgesamt 64 Bits s exponent 1 Bit 11 Bits fraction 52 Bits Bit‐Aufteilungen in dieser Form sind in IEEE 754 spezifiziert. Betrachte die wissenschaftliche, normalisierte Darstellung: [+ oder ‐] 1,xxxxxxxx * 2yyyy Beobachtung: die „1“ vor dem Komma ist redundant. Somit: Bei IEEE 754 wird die „1“ implizit angenommen und in „fraction“ nicht codiert. „fraction“ speichert nur Nachkommastellen. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 101 Beispiel s exponent fraction 1 Bit 8 Bits 23 Bits Es sei die „1“ vor dem Komma implizit angenommen. „Fraction“ speichere damit nur die Nachkommastellen. Was ist der Dezimalwert x des folgenden Bit‐Strings? 1000001010110000000000000000000 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 102 Weitere Eigenschaften von IEEE 754 Unterscheidung von „Fraction“ und „1+Fraction“ in der Darstellung (‐1)S * (1 + Fraction) * 2Exponent 1+Fraction wird als Significant (deutsch: Mantisse) bezeichnet. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 103 Motivation für eine geeignete Exponent‐Darstellung Annahme: Exponent wäre mit Zweierkomplement dargestellt. Wie macht man einen Größer‐Kleiner‐Vergleich der folgenden beiden Zahlen? Zahl 1: 000000111101000100000000000000000 Zahl 2: 011010111010010000010000000000000 1. Vergleiche erst mal die Vorzeichenbits. Bei unterschiedlichen Vorzeichenbits ist der Vergleich beendet. 2. Vergleiche die Exponenten. Ist einer größer als der andere, ist der Vergleich beendet. (Signed‐Vergleich) 3. Vergleiche die Fractions. (Unsigned‐Vergleich) Kann man Schritt 2 und 3 in einem durchführen? Kleinster Exponent müsste 00000000 und größter Exponent müsste 11111111 sein, dann könnte man Exponent und Fraction für einen Vergleich einfach konkatenieren. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 104 Darstellung des Exponenten in Biased‐Notation Erinnerung: Biased‐Notation (hier mit 8‐Bit und Bias 127): 0000 0000 = 0000 0001 = ... 0111 1110 = 0111 1111 = 1000 0000 = ... 1111 1110 = 1111 1111 = -127 -126 (0-Bias = -127) (1-Bias = -126) -1 0 1 (126-Bias = -1) (127-Bias = 0) (128-Bias = 1) 127 128 (254-Bias = 127) (255-Bias = 128) Zusammengefasst: Der Wert x einer Zahl in IEEE 754 Darstellung ist (Single‐Precision (8‐Bit‐Exponent) Bias=127, Double‐Precision (11‐Bit‐Exponent) Bias=1023) Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 105