Darstellung von negativen binären Zahlen

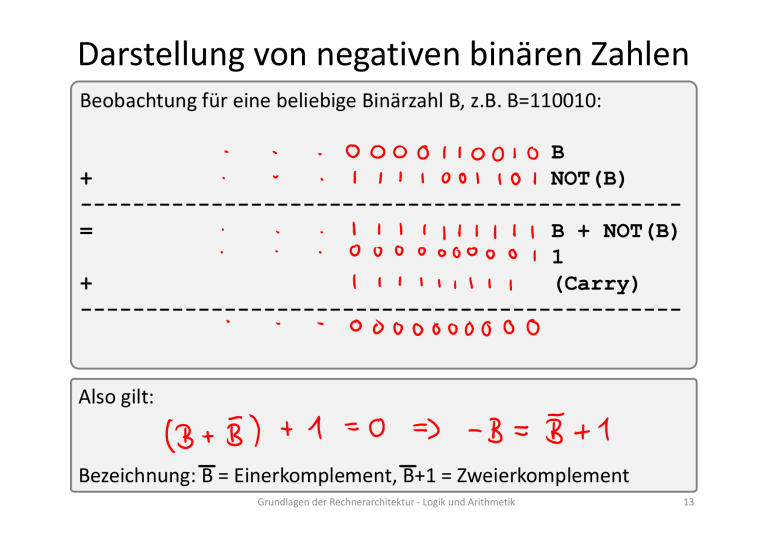
Darstellung von negativen binären Zahlen
Beobachtung für eine beliebige Binärzahl B, z.B. B=110010:
B
+
NOT(B)
---------------------------------------------=
B + NOT(B)
1
+
(Carry)
----------------------------------------------
Also gilt:
Bezeichnung: B = Einerkomplement, B+1 = Zweierkomplement
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
13
Quiz
Zweierkomplement‐Binärzahl B=...1111011 als Dezimalzahl?
Was ist die Dezimalzahl –7 als Binärzahl B in Zweierkomplement?
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
14
Subtraktion von binären Zahlen nochmal
Beispiel C = A – B:
-
1
1
1
0
1
1
0
0
1
1
0
1
(A)
(B)
Bestimme Zweierkomplement zu B, also –B:
Also ist C:
(Carry)
(A)
(-B)
1
1
1
0
1
0
+ ... 1
1
0
1
0
1
0
1
-----------------------------------=
(C)
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
15
N‐Bit binäre Zahlen (signed)
n‐Bit‐Darstellung ist ein Fenster auf die ersten n Stellen der Binär‐Zahl
…0000000000000000000000000000000000000000000000000110 =
6
…1111111111111111111111111111111111111111111111111101 = -3
Beispiel: 16‐Bit
MSB bestimmt das Vorzeichen. MSB=0 bedeutet nicht‐negativ, MSB=1 bedeutet negativ.
Beispiel vorzeichenbehaftete 8‐Bit‐Binärzahlen:
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 1
.
.
.
0 1 1 1 1 1 0
0 1 1 1 1 1 1
0 1 1 1 1 1 1
0 = 0
1 = 1
0 = 2
1 = 125
0 = 126
1 = 127
1 0 0 0 0 0 0
1 0 0 0 0 0 0
1 0 0 0 0 0 1
.
.
.
1 1 1 1 1 1 0
1 1 1 1 1 1 1
1 1 1 1 1 1 1
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
0 = -128
1 = -127
0 = -126
1 = -3
0 = -2
1 = -1
16
Nicht‐vorzeichenbehaftete Zahlen (unsigned)
n‐Bit‐Darstellung ist ein Fenster auf die ersten n Stellen der Binär‐Zahl
…0000000000000000000000000000000000000000000000000110 = 6
…0000000000000000000000000000000000001111111111111101 = 65533
Beispiel: 16‐Bit
MSB bestimmt das Vorzeichen nicht. Zahl ist immer nicht‐negativ.
Beispiel nicht‐vorzeichenbehaftete 8‐Bit‐Binärzahlen:
0 0 0 0 0 0 0
0 0 0 0 0 0 0
0 0 0 0 0 0 1
.
.
.
0 1 1 1 1 1 0
0 1 1 1 1 1 1
0 1 1 1 1 1 1
0 = 0
1 = 1
0 = 2
1 = 125
0 = 126
1 = 127
1 0 0 0 0 0 0
1 0 0 0 0 0 0
1 0 0 0 0 0 1
.
.
.
1 1 1 1 1 1 0
1 1 1 1 1 1 1
1 1 1 1 1 1 1
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
0 = 128
1 = 129
0 = 130
1 = 253
0 = 254
1 = 255
17
Signed‐N‐Bit Binär in Dezimal umrechnen
Beispiel 8‐Bit‐Binärzahl B:
1 1 1 1 1 1 0 1 binär ist dezimal:
Beobachtung für folgende 8‐Bit‐Zahl C (Erinnerung: 10000000 binär ist –128):
1 0 0 0 0 1 0 1
Also für signed n‐Bit‐Binärzahl b = bn‐1 bn‐2 ... b0 gilt:
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
18
Sign‐Extension
Gegeben 6 und –3 in 16‐Bit‐Darstellung.
0000000000000110
6 in 16‐Bit‐Binärdarstellung
1111111111111101
–3 in 16‐Bit‐Binärdarstellung
Wie sieht die 32‐Bit‐Binärdarstellung aus?
6 in 32‐Bit‐Binärdarstellung?
–3 in 32‐Bit‐Binärdarstellung?
Erinnerung: n‐Bit‐Darstellung ist ein Fenster auf die ersten n Stellen der Binär‐Zahl
…0000000000000000000000000000000000000000000000000110 =
6
…1111111111111111111111111111111111111111111111111101 = -3
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
19
Arithmetischer Rechts‐Shift
Arithmetischer Rechts‐Shift von b um x Stellen:
Verschiebe Bits nach rechts, um den angegeben Wert x.
Die neuen leeren Stellen werden mit dem Sign‐Bit aufgefüllt.
Arithmetischer Rechts‐Shift am Beispiel von 8‐Bit‐Zahlen:
Arithmetischer Rechts‐Shift um 2 Stellen:
0 1 0 0 1 1 1 1 -->
Arithmetischer Rechts‐Shift um 2 Stellen:
1 1 1 1 0 0 0 1 -->
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
20
Overflow
Einschränkung auf n‐Bit kann einen Overflow bei Addition erzeugen:
(Carry)
0 1 0 1 1 0 1 0
(A)
+
(B)
0 1 1 0 0 1 1 1
-------------------------=
(C)
Addition von negativer und nicht‐negativer Zahl. Overflow möglich?
Overflow erfordert, dass mindestens gilt:
Also Overflow in diesem Fall nicht möglich.
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
21
Overflow
Subtraktion von zwei negativen Zahlen x und y. Overflow möglich?
Der Fall „zwei nicht‐negativen Zahlen“ ist analog.
Also: Overflow in diesem Fall nicht möglich.
Zusammenfassung: Wann kann ein Overflow eintreten?
Operation Operand A Operand B
Ergebnis welches Overflow anzeigt
A+B
≥0
≥0
< 0
A+B
<0
<0
≥0
A–B
≥0
< 0
< 0
A–B
< 0
≥0
≥0
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
22
Randbemerkung
Andere Darstellungsformen für negative Binärzahlen:
• Einerkomplement: Negativer Wert von B ist NOT(B)
• Sign‐and‐Magnitude: MSB ist das Vorzeichen. Rest ist der Wert.
• Biased‐Notation (Beispielsweise mit 0 auf 1000...0000):
0000 0000 0000 0000 0000 0000 0000 0000 = kleinster negativer Wert
0000 0000 0000 0000 0000 0000 0000 0001 = kleinster negativer Wert + 1
...
0111 1111 1111 1111 1111 1111 1111 1111 = ‐1
1000 0000 0000 0000 0000 0000 0000 0000 = 0
1000 0000 0000 0000 0000 0000 0000 0001 = 1
...
1111 1111 1111 1111 1111 1111 1111 1110 = größter positiver Wert ‐1
1111 1111 1111 1111 1111 1111 1111 1111 = größter positiver Wert
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
23
Logische Bausteine
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
24
Logische Bausteine
Kombinatorische Schaltungen
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
25
Gatter
Funktion Eingabe Symbol Ausgabe
AND
A
A AND B
Verallgemeinerung auf n Eingänge
A1
A2
A1 AND A2 ... AND An
B
Und‐Gatter
OR
A
An
B
A1
A2
Oder‐Gatter
NOT
Und‐Gatter mit n Eingängen
A OR B
NOT A
A
Inverter
A1 OR A2 ... OR An
An
Oder‐Gatter mit n Eingängen
Bildquelle: Symbole kopiert aus David A. Patterson und John L. Hennessy, „Computer Organization and Design“, Fourth Edition, 2012
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
26
Kombinatorische Schaltungen
Jede boolesche Funktion (gegeben als logischer Ausdruck) wie z.B. f(A,B) = NOT( NOT(A) OR B)
Lässt sich als kombinatorische Schaltung realisieren. Das Beispiel:
Inverter werden häufig abgekürzt dargestellt. Das Beispiel:
Bildquelle: Symbole kopiert aus David A. Patterson und John L. Hennessy, „Computer Organization and Design“, Fourth Edition, 2012
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
27
Wahrheitstabellen
Jede boolesche Funktion lässt mit einer Wahrheitstabelle darstellen.
Beispiel: f(A,B,C) = A AND NOT(B OR C) als Wahrheitstabelle
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C B OR C NOT(B OR C) f(A,B,C)=A AND NOT(B OR C)
0
1
0
1
0
1
0
1
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
28
Wahrheitstabellen
Jede Wahrheitstabelle kann man mit einem logischen Ausdruck
darstellen. Beispiel:
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C f(A,B,C)
0
1
1
1
0
0
1
1
0
1
1
0
0
1
1
1
Als Disjunktive Normalform (DNF); Oder‐
Verknüpfung aller Minterme:
Ziel ist aber nicht irgend einen Ausdruck zu finden, sondern einen möglichst kleinen (also eine möglichst kleine kombinatorische Schaltung). Mehr dazu gleich.
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
29
Wahrheitstabellen
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C f(A,B,C)
0
1
1
1
0
0
1
1
0
1
1
0
0
1
1
1
Neben der disjunktiven Normalform gibt es noch die Konjunktive Normalform (KNF); Und‐Verknüpfung aller Maxterme
Allgemein: für den Entwurf von digitalen Schaltungen verwendet man in der Regel eine Darstellung von booleschen Funktionen mittels Normalformen.
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
30
Wahrheitstabellen
Bei der Suche nach möglichst kleinen kombinatorischen Schaltungen
können auch sogenannte Don‘t ‐Care‐Terme recht hilfreich sein.
A
0
0
0
0
1
1
1
1
B
0
0
1
1
0
0
1
1
C f(A,B,C)
0
1
1
1
0
0
1
X
0
1
1
X
0
X
1
1
Don‘t‐Care Terme: In der kombinatorischen Schaltung, die diese Funktion implementiert, ist es egal welche Ausgabe die Schaltung für die Eingaben 011, 101 und 110 produziert.
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
31
Wahrheitstabellen
In einer Wahrheitstabelle kann für die Eingaben auch mehrere
Ausgabe‐Bits festgelegt werden. Beispiel:
Eingabe
Bit 0
0
0
0
0
1
1
1
1
Eingabe
Bit 1
0
0
1
1
0
0
1
1
Eingabe Ausgabe Ausgabe
Bit 2
Bit 0
Bit 1
0
1
1
1
1
1
0
0
1
1
0
1
0
1
0
1
1
1
0
1
0
1
1
0
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
32
Beispiel: Addition zweier Bits mit Übertrag
Wahrheitstabelle
A
0
0
1
1
Boolesche Ausdrücke
B s(A,B)=A+B c(A,B)=Carry
0
1
0
1
Kombinatorische Schaltung
Ist das eine gute Schaltung?
Wie sieht n‐Bit‐Addition aus?
Mehr dazu gleich.
(Im Folgenden nehmen wir häufig logische Bauelemente als Blackbox mit Eingängen und Ausgängen an. Die Funktion des Bausteins wird nur textuell beschrieben.)
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
33
Logische Bausteine
Minimierung
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
34
Minimierung mittels Rechenregeln
Beispiel: Minimierung der folgenden DNF
(!A * !B * C) + (!A * B * !C) + (A * !B * !C) + (A * !B * C) + (A * B * !C) Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
35
Minimierung mittels KV‐Diagramm
A
B
C
D
f(A,B,C,D)
0
0
0
0
1
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
0
0
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
1
1
1
0
1
0
1
1
1
0
1
1
1
1
1
1
Ordne Variablen einer 2‐, 3‐ oder 4‐Stelligen Funktion in Tabelle so an, dass sich benachbarte Felder nur in einer Variablen unterscheiden.
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
36
Minimierung mittels KV‐Diagramm
A
B
C
D
f(A,B,C,D)
0
0
0
0
1
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
1
1
1
0
1
0
1
1
1
0
1
1
1
1
1
1
Trage für alle Minterme eine 1 in dem Diagramm ein.
A
A
D
C
D
C
D
B
B
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
B
37
Minimierung mittels KV‐Diagramm
A
B
C
D
f(A,B,C,D)
0
0
0
0
1
0
0
0
1
1
0
0
1
0
0
0
0
1
1
0
0
1
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
0
1
0
1
0
0
1
0
1
1
0
1
1
0
0
1
1
1
0
1
0
1
1
1
0
1
1
1
1
1
1
Fasse benachbarte 1en zu den größtmöglichen Blöcken der Größe 2^n zusammen.
A
C
1
A
1
1
1
1
1
C
D
1
D
1
B
B
Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik
D
B
38