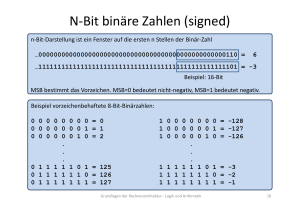
Darstellung von vorzeichenbehafteten Ganzzahlen

Darstellung von vorzeichenbehafteten Ganzzahlen
1.2 Darstellung von vorzeichenbehafteten Ganzzahlen
Für viele Anwendungen muss der Bereich der Zahlen um die negativen Ganzzahlen erweitert werden.
Negative ganze Zahlen werden im Rechner in einer speziellen Weise dargestellt.
Diese spezielle Darstellung ergibt sich aus der Forderung, im Rechner das gleiche
Addierwerk für vorzeichenlose und vorzeichenbehaftete Zahlen einzusetzen.
Dazu wird der zur Verfügung stehende Bereich in zwei gleich große Portionen unterteilt. Bei 16 Bit
Wortlänge sieht das folgendermaßen aus:
+ + + + + + + + + + + + + + + + + + + + ----------------------------------------------------+ + + + + + positiver + + + + + + + + + + --------------------- negativer ------------------+ + + + + + Bereich + + + + + + + + + + --------------------- Bereich --------------------+ + + + + + + + + + + + + + + + + + + + ----------------------------------------------------hex. 0
bis
7FFF
8000
bis
FFFF
Die Erweiterung um die negativen Zahlen geht also auf Kosten des absolut
darstellbaren Bereichs. Er beträgt bei 16 Bit Wortlänge:
- 32768,...,0,...,+ 32767
Die Null wird den positiven Zahlen zugerechnet.
Negative Zahlen erkennt man daran, dass das MSB (Most Significant Bit den Wert „1“ besitzt.
LSB bedeutet Least Significant Bit.
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
0
1
MSB
LSB
Negative Zahl -> MSB = 1
Positive Zahl
-> MSB = 0
Diese Darstellung ist also wortlängenabhängig! Im Rechner geschieht dies durch die Angabe der Wortlänge, d. h. durch die Angabe der Anzahl der Bits, die zur Darstellung einer Zahl verfügbar ist
(n-Bit-System).
Allgemeine Regel:
Schritt 1:
Schritt 2:
Schritt 3:
+
1
Absolutbetrag der gesuchten Zahl im n-Bit-Sytem
Bitmuster komplementieren (1er-Komplement)
addieren
negative Zahl
Daher nennt man diese Art der Zahlencodierung 2er-Komplement-Darstellung.
Die Berechnung lässt sich, v. a. im Hexadezimalsystem, auch so durchführen (Regel b):
Schritt 1:
Schritt 2:
Schritt 3:
Beispiel
–
+
=
„größte“ Zahl bei gegebener Wortlänge
Absolutbetrag der gesuchten Zahl
1
2er-Komplement
Darstellung von -110 in einem 16-Bit-System binär:
1:
komplementieren:
+1:
-1:
0000 0000 0000 0001
1111 1111 1111 1110
1 +
1111 1111 1111 1111