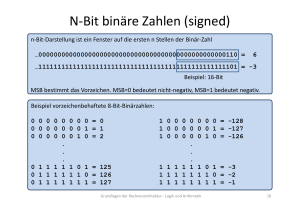
IEEE 754 Rounding-Modes
Werbung
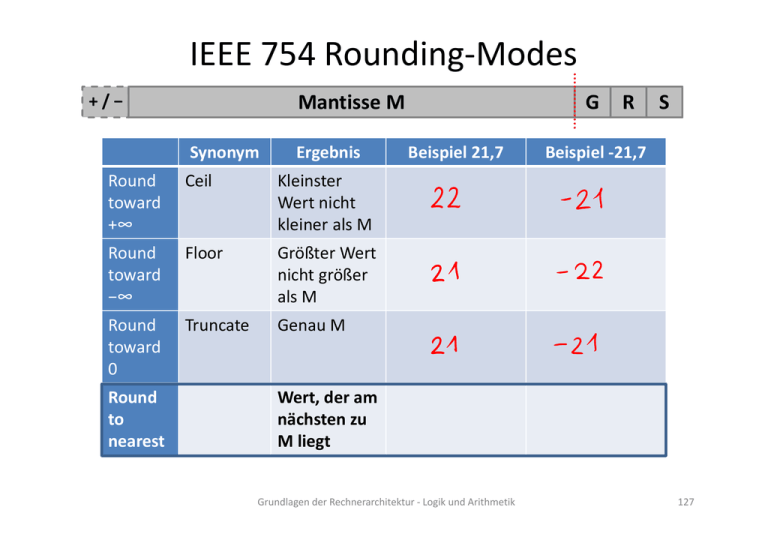
IEEE 754 Rounding‐Modes Mantisse M + / − Synonym Ergebnis Round toward +∞ Ceil Kleinster Wert nicht kleiner als M Round toward −∞ Floor Größter Wert nicht größer als M Round toward 0 Truncate Genau M Round to nearest G Beispiel 21,7 R S Beispiel ‐21,7 Wert, der am nächsten zu M liegt Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 127 IEEE Rounding‐Modes: Round to Nearest Mantisse G R S Eingabe Form bei Tie Rundung Mantisse|000 Same Mantisse|001 Down Mantisse|010 Down Mantisse|011 Down Mantisse|100 ...0|100 Down (Tie) ...1|100 Up Ergebnis M M = Mantisse M = Mantisse M = Mantisse M = Mantisse M = Mantisse M = Mantisse + 1 Mantisse|101 Mantisse|110 Mantisse|111 M = Mantisse + 1 M = Mantisse + 1 M = Mantisse + 1 Up Up Up Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 128 Quiz Was ist das Rundungsergebnis bei Round‐to‐Nearest für folgende Instanzen von „8‐Bit‐Mantisse | Guard‐Round‐Sticky“? A.) 0000 1101 | 110 GRS B.) 0011 0011 | 100 Richtung 001 Down 010 Down 011 Down 100 C.) 0101 0101 | 010 Mantisse ...0 Down ...1 Up 101 Up 110 Up 111 Up Übersicht zu Round‐to‐Nearest Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 129 Beispiel für die Genauigkeitssteigerung Wir betrachten 8‐Bit Mantissen. Zu addieren sei: 1,100 0110 * 26 (dezimal = 99,0000) + 1,011 1010 * 22 (dezimal = 5,8125) (Summe dezimal = 104,8125) Das Mantissen‐Alignment und GRS‐Bits kennen wir schon, also: Rechnung: Mantisse|GRS Mantisse 11000110|000 11000110 + 00001011|101 + 00001011 ----------------------11010001|101 11010001 Rundung: 11010010 ohne 11010001 Ergebnis: 1,1010010 * 26 1,1010001 * 26 Dezimal : 105,0 104,5 Also hat man mit GRS‐Bits und Rundung einen Abstand von 105,0 – 104,8125 = 0,1875. Ohne GRS‐Bits und Rundung ist der Abstand 104,8125 – 104,5 = 0,3125. Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 130 Denormalized‐Numbers Kleinste mit IEEE754 Single‐Precision darstellbare normalized Zahl > 0: 1,000 0000 0000 0000 0000 0000 * 2−126 Der Exponent −127 ist für die 0 reserviert; die Fraction ist dabei 0: .,000 0000 0000 0000 0000 0000 * 2−127 Warum die Fraction für Exponent −127 nicht sinnvoll nutzen? Eine Denormalized‐Number der Form .,000 1010 1110 1000 1111 0011 * 2−127 bedeutet: 0,000 1010 1110 1000 1111 0011 * 2−126 Somit, kleinste mit IEEE754 Single‐Precision darstellbare Zahl > 0: 0,000 0000 0000 0000 0000 0001 * 2−126 = 1,0 * 2−149 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 131 Quiz Was ist mit denormalized Numbers bei IEEE 754 Double‐Precision die kleinste darstellbare Zahl > 0? Erinnerung: IEEE 754 Double‐Precision: Fraction: 52 Bits Exponent‐Bias: 1023 Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 132 Webseiten‐Tipp zum Üben users‐tima.imag.fr/cis/guyot/Cours/Oparithm/english/Flottan.htm Floating point numbers format Rounding to the nearest Addition and subtraction Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 133 Zusammenfassung und Literatur Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 134 Zusammenfassung • Rechnerarithmetik endlich und stimmt damit nicht exakt mit Arithmetik über reellen Zahlen überein – Häufig Approximation realer Zahlen – Assoziativgesetz gilt z.B. nicht – Hat z.B. Konsequenz auf paralleles Rechnen • Beschränkter Zahlenbereich – Overflow, Underflow • Wichtigste Entwicklung über die Jahre – Zweierkomplement und IEEE 754 – In jedem modernen Computer so Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 135 Quiz Annahme es gäbe ein 16‐Bit IEEE 754 Floating‐Point‐Format mit 5 Bits für den Exponenten. Welcher Zahlenbereich wird durch dieses Format abgedeckt? 20 A: 1.0000 0000 00 * bis 1.1111 1111 11 * 231, 0 C: +/‐ 1.0000 0000 00 * 2‐14 bis +/‐ 1.1111 1111 11 * 215, +/‐ 0, +/‐ , NaN B: +/‐ 1.0000 0000 0 * 2‐14 bis +/‐ 1.1111 1111 1 * 215 +/‐ 0, +/‐ , NaN D: +/‐ 1.0000 0000 0 * 2‐15 bis +/‐ 1.1111 1111 1 * 214, +/‐ 0, +/‐ , NaN Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 136 Literatur [PattersonHennessy2012] David A. Patterson und John L. Hennessy, „Computer Organization and Design“, Fourth Edition, 2012 2.4 Signed and Unsigned Numbers 2.6 Logical Operations 3.1 Introduction 3.2 Addition and Subtraction 3.3 Multiplication 3.4 Division 3.5 Floating Point 3.6 Parallelism and Computer Arithmetic: Associativity Grundlagen der Rechnerarchitektur ‐ Logik und Arithmetik 137