Vorlesung "Mathematik und Statistik" WS 2006 / 2007 Teil II

Vorlesung
"Mathematik und Statistik"
WS 2006 / 2007
Teil II
Statistik und Stochastik
Oktober 2006
Dozent: Dr. Norbert Marxer
2
Skript Statistik und Stochastik
0. Inhaltsverzeichnis
0. Inhaltsverzeichnis .................................................................................................
2
1. Einleitung ..................................................................................................................
7
Vorbemerkung ...............................................................................................
Einleitung ..........................................................................................................
Referenzen ......................................................................................................
7
7
9
2. Wahrscheinlichkeitstheorie .............................................................................. 10
Was ist Wahrscheinlichkeit? ................................................................. 10
Ergebnisraum und Ereignisraum .......................................................... 11
Zufallsexperiment ......................................................................................... 11
Illustration: Drei Mal eine Münze Werfen ................................................. 12
Illustration: Zwei Mal Würfeln ................................................................ 12
Empirisches Gesetz der grossen Zahlen ....................................................... 13
Kolmogorov'sches Axiomensystem ..................................................... 13
Eigenschaften von Wahrscheinlichkeitsmassen ............................................ 14
Beispiel 1 .............................................................................................. 14
Beispiel 2 .............................................................................................. 14
Venn Diagramme .......................................................................................... 15
3. Elementare Kombinatorik .................................................................................. 16
Einleitung .......................................................................................................... 16
Laplace Experimente .................................................................................. 16
Laplace Wahrscheinlichkeit .........................................................................
Mehrstufige Laplace Experimente - Baumdiagramme .................................
Bernoulli Experimente ................................................................................
Summenregel .................................................................................................
Produktregel ....................................................................................................
Permutationen und Binomialverteilung ..............................................
16
17
17
17
18
18
Einleitung .....................................................................................................
Kombinatorik ........................................................................................
Mengenlehre ..........................................................................................
Ohne Zurücklegen - alle verschieden ...........................................................
Beispiel .................................................................................................
Ohne Zurücklegen - mehrere Klassen ...........................................................
Ohne Zurücklegen - mit 2 Klassen ...............................................................
18
18
19
19
19
19
20
Urnenexperimente bei verschiedenen Elementen ....................... 20
Urnenexperimente ........................................................................................
Mit Zurücklegen und Geordnet (k-Tupel) ....................................................
Beispiel .................................................................................................
Mit Zurücklegen und Ungeordnet (k-Repetition) .........................................
Beispiel .................................................................................................
Ohne Zurücklegen und Geordnet (k-Permutation) .......................................
Beispiel .................................................................................................
Ohne Zurücklegen und Ungeordnet (k-Kombinationen) ..............................
20
20
21
21
21
21
22
22
3
Skript Statistik und Stochastik
Beispiel .................................................................................................
Zusammenfassung - Ziehen mit verschiedenen Elementen ...........................
22
22
Verteilungen in Behälter ............................................................................ 23
Beispiel .................................................................................................
23
Urnenexperimente bei teilweise gleichen Elementen ................. 24
Einleitung ..................................................................................................... 24
Ziehen mit Zurücklegen - Variationen und Kombinationen ......................... 24
Beispiel ................................................................................................. 25
Beispiel ................................................................................................. 25
Ziehen ohne Zurücklegen - Variation und Kombination .............................. 25
Beispiel ................................................................................................. 25
Beispiel ................................................................................................. 25
4. Bedingte Wahrscheinlichkeiten ...................................................................... 26
Einleitung .......................................................................................................... 26
Bedingte Wahrscheinlichkeit .................................................................. 26
Beispiel .................................................................................................
27
Stochastische Unabhängigkeit .............................................................. 27
5. Zufallszahlengenerator ....................................................................................... 28
Einleitung .......................................................................................................... 28
6. Zufallsvariablen und ihre Verteilungen ........................................................ 29
Einleitung .......................................................................................................... 29
PDF und CDF ................................................................................................. 30
Diskrete Verteilung ................................................................................
33
Erwartungswert .............................................................................................. 33
Beispiel Würfeln ..........................................................................................
34
Diskrete Verteilungen ................................................................................. 34
Einleitung .....................................................................................................
Gleichverteilung (DiscreteUniformDistribution) ..........................................
Einleitung ..............................................................................................
Eigenschaften ........................................................................................
Bernoulli Verteilung (BernoulliDistribution) ...............................................
Einleitung ..............................................................................................
Eigenschaften ........................................................................................
Binomial Verteilung (BinomialDistribution bzw. BINOMVERT) ...............
Einleitung ..............................................................................................
Eigenschaften ........................................................................................
Die Anzahl der Erfolge beim n-maligen Münzen werfen. ...........................
Beispiel 1 ..............................................................................................
Beispiel 2 ..............................................................................................
Beispiel 3 ..............................................................................................
Poisson Verteilung (PoissonDistribution bzw. POISSON) ..........................
Einleitung ..............................................................................................
Eigenschaften ........................................................................................
34
35
35
36
36
36
37
38
38
39
39
39
40
40
41
41
41
Stetige Verteilungen .................................................................................... 41
Einleitung ..................................................................................................... 41
Normalverteilung (NormalDistribution bzw. NORMVERT, STANDNORMVERT)
....................................................................................................................... 42
4
Skript Statistik und Stochastik
Einleitung ..............................................................................................
Eigenschaften ........................................................................................
Standardnormalverteilung .......................................................................
c2 Verteilung (ChiSquareDistribution bzw. CHIVERT) .............................
Einleitung ..............................................................................................
Eigenschaften ........................................................................................
Student t Verteilung (StudentTDistribution bzw. TVERT) ..........................
Eigenschaften ........................................................................................
42
43
43
44
44
44
44
45
Zentraler Grenzwertsatz ............................................................................ 46
Einleitung .....................................................................................................
Experiment ...................................................................................................
Kugeln aus einer Urne ziehen .......................................................................
46
46
47
7. Statistik und empirische Daten ....................................................................... 49
Einleitung .......................................................................................................... 49
Datentypen ...................................................................................................... 50
8. Beschreibende Statistik ...................................................................................... 51
Einleitung .......................................................................................................... 51
Graphische Darstellungen ....................................................................... 52
Einleitung .....................................................................................................
Diskrete Datenreihe (n klein) ...................................................................
Diskrete Daten (n gross: 1000) ................................................................
Stetige Daten (n gross: 1000) ..................................................................
8i, xi < .............................................................................................................
Diskrete Daten (n klein) ..........................................................................
Diskrete Daten (n gross) .........................................................................
Stetige Daten (n gross) ............................................................................
8i, xsort,i < ........................................................................................................
Diskrete Daten (n klein) ..........................................................................
Diskrete Daten (n gross) .........................................................................
Stetige Daten (n gross) ............................................................................
Häufigkeitsfunktionen: 8xsort,i , ni <, 8xi , hi < ...................................................
Diskrete Daten (n klein) ..........................................................................
Diskrete Daten (n gross) .........................................................................
Stetige Daten (n gross) ............................................................................
Verteilungsfunktion: 8xi , ⁄ij=1 h j < .................................................................
52
52
53
53
53
53
54
54
55
55
55
56
56
57
58
59
61
Weitere graphische Darstellungen ................................................................ 62
Box-And-Whisker Plot ........................................................................... 62
Masszahlen - Nominalskala .................................................................... 63
Masszahlen - Ordinalskala ...................................................................... 64
Masszahlen - Metrisch skalierte Daten .............................................. 65
Lagemasse (Lokalisationsmasse) ..................................................................
Streuungsmasse ............................................................................................
Formmasse ....................................................................................................
Zentrierung und Standardisierung ................................................................
Additionssätze für êêx und s2 ..........................................................................
65
68
71
73
73
Daten mit diskreter Klassierung und
Stetig klassierte Daten .............................................................................. 74
Daten mit diskreter Klassierung ...................................................................
74
5
Skript Statistik und Stochastik
Stetig klassierte Daten .................................................................................
74
Konzentrations- und Disparitätsmessung ......................................... 77
Konzentration ...............................................................................................
Disparität ......................................................................................................
Zusammenhang zwischen Konzentrationsindizes und Disparitätkoeffizienten
.......................................................................................................................
Kurven ..................................................................................................
Zahlen ...................................................................................................
Gemeinsame Prinzipien ..........................................................................
Unterschiede ..........................................................................................
77
79
80
80
80
80
81
9. Induktive Statistik .................................................................................................. 82
Einleitung .......................................................................................................... 82
Punktschätzungen ....................................................................................... 83
Punktschätzung für den Mittelwert ...............................................................
Punktschätzung für den Anteilswert .............................................................
Punktschätzung für die Varianz ....................................................................
Eigenschaften von Punktschätzungen ...........................................................
83
83
83
84
Intervallschätzungen ................................................................................... 84
Einleitung .....................................................................................................
Stichprobenverteilungen ...............................................................................
Verteilung des Stichprobenmittelwerts .....................................................
Lösung a ...............................................................................................
Lösung b ...............................................................................................
Intervallschätzung bei grossen Stichproben .................................................
Intervallschätzung bei kleinen Stichproben ..................................................
Lösung ..................................................................................................
84
84
84
85
85
86
86
87
Statistische Tests ......................................................................................... 87
Einleitung ..................................................................................................... 87
Testen von Hypothesen über Mittelwerte ..................................................... 88
Zweiseitige Fragestellung ........................................................................ 88
Beispiel ................................................................................................. 88
Schritte ................................................................................................. 90
10. Zweidimensionale Verteilungen ................................................................... 91
Einleitung .......................................................................................................... 91
Kontingenztabelle ......................................................................................... 92
Einleitung .....................................................................................................
Randverteilung .............................................................................................
Bedingte Wahrscheinlichkeiten ....................................................................
Berechnung von Mittelwerten und Varianzen für X und Y ..........................
92
92
93
94
Kovarianz und Korrelationskoeffizient ................................................ 94
Einleitung .....................................................................................................
Beispiel 1 ......................................................................................................
Beispiel 2 ......................................................................................................
94
95
96
11. Regression und Korrelation ........................................................................... 97
Einleitung .......................................................................................................... 97
Scatter Plot ...................................................................................................... 98
Korrelation ........................................................................................................ 99
6
Skript Statistik und Stochastik
Einleitung .....................................................................................................
Berechnung des Korrelationskoeffizienten ...................................................
Grenzen der Korrelationsanalyse ..................................................................
Nichtlinearität ........................................................................................
Ausreisser .............................................................................................
Signifikanz des Korrelationskoeffizienten ....................................................
99
99
100
101
101
102
(Lineare) Regression .................................................................................. 103
Einleitung .....................................................................................................
`
`
Berechnung der (geschätzten) Regressionskoeffizienten b0 und b1 ..............
Eigenschaften der Regressionsgerade .......................................................
Berechnung der Residualvarianz s2 (standard error of estimate) .................
`
`
Berechnung der Varianzen für b0 und b1 ......................................................
Bestimmtheitsmass R2 (coefficient of determination) ..................................
Intervallschätzung und Tests ........................................................................
Prognose .......................................................................................................
`
`
Mathematica Lineare Regression - b0 und b1 Berechnungen .......................
Beispiel mit Covariance und Mean ...........................................................
103
104
105
105
106
106
108
109
110
110
12. Zeitreihen ................................................................................................................ 111
Einleitung .......................................................................................................... 111
Trendschätzung ............................................................................................
Saisonale Variation .......................................................................................
Zyklische Variation ......................................................................................
Irreguläre Variaton .......................................................................................
Achtung bei Extrapolationen ........................................................................
Simulation ....................................................................................................
111
112
112
112
112
113
13. Stochastische Differentialgleichungen ..................................................... 114
Einleitung .....................................................................................................
Aktie .............................................................................................................
Stochastiche Differentialgleichung ...........................................................
Brown'sche Bewegung ............................................................................
Monte-Carlo Lösung der SDE ................................................................
Symbolische Lösung der SDE .................................................................
Mehrere Aktien ......................................................................................
114
114
114
115
115
116
117
Skript Statistik und Stochastik
7
1. Einleitung
Vorbemerkung
Die Vorlesung "Mathematik und Statistik", die im WS 2006 / 2007 an der Hochschule Liechtenstein angeboten wird,
beinhaltet nach einer allgemeinen Repetition von vorausgesetzten mathematischen Grundlagen die Gebiete Taylor
Entwicklung und Partielle Differentiation, Zeitreihenanalyse, Regression und allgemeine Optimierung sowie aus dem
Gebiet der Statistik und Stochastik die Gebiete Deskriptive Statistik, Induktive Statistik und Stochastic Calculus.
Der ganze Vorlesungsstoff wird in zwei Dokumenten bzw. Skripten präsentiert.
Das mit "Skript Statistik" bezeichnete Dokument beinhaltet die Gebiete, die dem Gebiete der Statistik und Stochastik
zugerechnet werden können.
Das mit "Skript Abbildungen" bezeichnete Dokument beinhaltet die Gebiete, die nicht dem Gebiete der Statistik und
Stochastik zugerechnet weden können.
Einleitung
Dieses Dokument ("Skript Statistik") enthält die Gebiete, die dem Gebiet der Statistik und Stochastik zugerechnet
werden können.
Die Graphik StatistikUebersicht.jpg zeigt, wie die verschiedenen (im Folgenden behandelten Themen) miteinander in
Beziehung stehen.
Einige Bemerkungen dazu:
† Sowohl Zufallsexperimente als auch empirische Befragungen liefern Daten zur Analyse mit den Methoden der
Beschreibenden Statistik.
† Die Induktive Statistik versucht aus Stichproben Aussagen über die empirische Verteilung der Grundgesamtheit zu
machen.
† Die Wahrscheinlichkeitstheorie liefert theoretische Verteilungen, die zum Teil auch für empirische Daten verwendet werden können.
Skript Statistik und Stochastik
8
Die Kapitel dieses Dokuments enthalten die folgenden Inhalte.
Das Kapitel "Wahrscheinlichkeitstheorie" nähert sich dem Begriff der Wahrscheinlichkeit und erklärt die wichtigen
Begriffe der Wahrscheinlichkeitstheorie wie Ergebnis, Ereignis und Wahrscheinlichkeit. Ausserdem wird mit dem
Kolmogorov'schen Axiomensystem die mathematische Grundlage der Wahrscheinlichkeitstheorie gelegt.
Das Kapitel "Elementare Kombinatorik" beschäftigt sich intensiv mit Zufallsexperimenten (vor allem Urnenexperimenten) und den dazugehörigen Formeln zur Berechnung von verschiedensten experimentellen Situationen.
Das Kapitel "Bedingte Wahrscheinlichkeiten" untersucht das Vorgehen, wenn Teilinformationen von Experimenten
vorliegen, gibt verschiedene Formeln dazu and und definiert den Begriff der stochastischen Unabhängigkeit.
Das Kapitel "Zufallszahlengenerator" ist ein kleiner Einschub, der Funktionen zur Erzeugung von Zufallszahlen, die
für spätere Simulationen und Computerexperimente wichtig sind, erklärt.
Das Kapitel "Zufallsvariablen und ihre Verteilungen" geht dann näher ein auf die wichtigen Funktionen PDF
(probability density function) und CDF (cumulative probability density function), die sowohl bei diskreten als auch bei
stetigen Verteilungen benutzt werden können, um aus Messintervallen auf Wahrscheinlichkeiten zu schliessen. Es wird
auch das umgekehrte Prozedere angesprochen, nämlich aus einem Wahrscheinlichkeitsbereich auf ein Messintervall zu
schliessen. Es werden auch die Begriffe Erwartungswert erklärt sowie die wichtigsten diskreten und stetigen Verteilungen diskutiert. Weiters wird der zentrale Grenzwertsatz anschaulich mit Computerexperimenten plausibilisiert.
Das Kapitel "Statistik und empirische Daten" beginnt dann die Behandlung von empirisch erhaltenen Daten. Nach
einer Übersicht über die Bereiche der Statistik wird auf die einzelnen Datentypen eingegangen.
Das Kapitel "Beschreibende Statistik" behandelt die Methoden, mit denen sich riesige Datenmengen anschaulich
mittels Graphiken oder kurz und prägnant mit Kennzahlen für die Lage und die Streuung der Daten sowie die Form der
Verteilung beschreiben lassen.
Das Kapitel "Induktive Statistik" behandelt die Methoden, wie sich aus einer Stichprobe auf die Eigenschaften der
Grundgesamtheit schliessen lässt. Es werden Punktschätzungen, bei denen es um die Abschätzung eines einzelnen
Werts (z.B. Mittelwert) geht, Intervallschätzungen, wo es um die Abschätzung von Konfidenzintervallen geht sowie
statistische Test, wo es um die Annahme bzw. Verwerfung von Hypothesen über die Grundgesamtheit geht, behandelt.
Die Induktive Statistik ist das Gebiet, wo die verschiedenen Methoden der vorangehenden Kapitel (Verteilungen, PDF,
CDF, Beschreibende Statistik etc.) eingesetzt werden können.
Das Kapitel "Zweidimensionale Verteilungen" beschäftigt sich mit multivariaten Daten, mit Kontingenztabellen und
Korrelationen von bivariaten Daten.
Das Kapitel "Zeitreihen" behandelt bivariate Daten und Zeitreihen sowie verschiedene Methoden, um aus diesen
Daten Informationen herauszuziehen.
Das Kapitel "Regression und Korrelation" behandelt bivariate Daten und Zeitreihen sowie verschiedene Methoden,
um aus diesen Daten Informationen herauszuziehen.
Abschliessend noch zwei Definitionen zum Titel dieses Notebooks
Die Statistik ist die Wissenschaft von der Gewinnung, Aufbereitung und Auswertung von Informationen / Daten. Viel mehr
dazu im Kapitel 7.
Die Stochastik ist die Beschreibung und Untersuchung von Zufallsexperimenten und deren Ausgang, von zeitlichen
Entwicklungen und räumlichen Strukturen, die wesentlich vom Zufall beeinflusst werden.
Skript Statistik und Stochastik
9
Referenzen
Das in der Vorlesung behandelte Gebiet ist sehr weit und es gibt natürlich eine Unmenge an Literatur zu den verschiedenen Themen.
So wie man sich im Wald dieser Literatur verlieren kann, so kann man sich auch im Wald einer zu langen Literaturliste
verlieren. Ich möchte deshalb im Folgenden nur sehr wenige, meines Erachtens nützliche, Hinweise geben.
Sehr kostengünstig sind natürlich die im Internet verfügbaren Informationen. Diese Informationen werden auch von
Jahr zu Jahr besser. Interessant sind sicherlich die unter
http://de.wikipedia.org/wiki/Mathematik
vorhandenen Beiträge: über Mengenlehre, Analysis, ...
Sehr gut und hilfreich können als Zusatzinformation zur Vorlesung im Gebiete der Statistik auch die beiden folgenden
Bücher (zusammen 600 Seiten) sein:
† "Wahrscheinlichkeitsrechnung und schliessende Statistik" von K. Mosler und F. Schmid, Springer, 2. Auflage,
2006.
www.uni-koeln.de/wiso-fak/wisostatsem/buecher/wrechng_schliessende/index.htm
† "Beschreibende Statistik und Wirtschaftsstatistik" von K. Mosler und F. Schmid, Springer, Berlin, 2. Auflage,
2005.
www.uni-koeln.de/wiso-fak/wisostatsem/buecher/beschr_stat/
Skript Statistik und Stochastik
10
2. Wahrscheinlichkeitstheorie
Was ist Wahrscheinlichkeit?
Wahrscheinlichkeitstheorie ist der Zweig der Mathematik, der sich mit Zufallsexperimenten befasst, mit ihrer Beschreibung und der Aufdeckung von Gesetzmässigkeiten. Es wird versucht mathematische Modelle zu finden für Experimente, bei denen mehrere verschiedene Verläufe möglich sind und deren Ergebnisse ganz oder teilweise vom Zufall
abhängen. Insbesondere sollen die Gesetzmässigkeiten bei vielfacher Wiederholung des Experiments aufgespürt
werden.
Bei einem Würfelexperiment kann nicht vorausgesagt werden, welche Augenzahl eintreten wird. Bei
vielfachen Wiederholungen des Experiments scheint jedoch der Anteil der Experimente, bei denen 1, 2,
... 6 gewürfelt wird, einer festen Grösse zuzustreben.
Eine zentrale und naheliegende Frage lautet: "Was ist Wahrscheinlichkeit?".
Auf diese Frage gibt es keine befriedigende Antwort. Intuitive Antworten können folgendermassen lauten.
Laplace'sche Wahrscheinlichkeitsdefinition
Ein unverfälschter (d.h. symmetrischer, unmanipulierter) Würfel werde geworfen und wir fragen nach der Wahrscheinlichkeit, dass die geworfene Augenzahl gerade ist. In diesem Beispiel wird wohl jeder antworten, dass die Wahrscheinlichkeit 50% sei, da die Hälfte der möglichen Ergebnisse (d.h. die Augenzahl 2, 4, 6) günstig und die andere Hälfte der
Ergebnisse (d.h. die Augenzahlen 1, 3, 5) ungünstig ist. Die Laplace'sche Wahrscheinlichkeit wird als Quotient der
Anzahl günstiger Ereignisse und der Anzahl möglicher Ereignisse definiert. Diese Definition bedeutet auch, dass alle
Ergebnisse eines Experiments gleich wahrscheinlich sind.
Wahrscheinlichkeit als relative Häufigkeit in einer endlichen Grundgesamtheit.
Eine andere intuitive Wahrscheinlichkeitsvorstellung folgt aus dem folgenden Beispiel. In einer Gruppe von 100'000
Personen seien 20'000 zwischen 10 und 20 Jahren alt. Wie gross ist die Wahrscheinlichkeit, dass eine zufällig aus der
Gruppe ausgewählte Person in diese Alterskategorie fällt. Intuitiv würde man sagen 20%, d.h. der Quotient aus 20'000
und 100'000, d.h. die relative Häufigkeit eines Merkmals in einer endlichen Grundgesamtheit (dazu mehr später). Auch
hier wird - wenn man nicht mehr dazu weiss - vorausgesetzt, dass jede der 100'000 Personen die gleiche Wahrscheinlichkeit hat, dieser Alterskategorie anzugehören.
Wahrscheinlichkeit als Grenzwert der relativen Häufigkeit bei wachsender Anzahl von Wiederholungen des Experiments
Bei den bisherigen zwei Möglichkeiten konnte man (oder musste man, da man keine Zusatzinformationen hatte) auf
Grund von Symmetrieeigenschaften annehmen, dass die Wahrscheinlichkeiten (eine bestimmte Augenzahl zu würfeln
bzw. einer bestimmten Alterskategorie anzugehören) gleich gross waren. Im folgenden Beispiel können keine solchen
Symmetrieeigenschaften verwendet werden. Es wird z.B. gefragt, wie gross die Wahrscheinlichkeit ist, dass beim Wurf
eines unsymmetrischen Gegenstands der Gegenstand auf einer bestimmten Fläche landet. Hier liefert uns weder die
Theorie (Symmetrie) noch die relative Häufigkeit einer endlichen Grundgesamtheit eine Antwort. Wir müssen das
Experiment durchführen und die relative Häufigkeit für eine grosse Anzahl an Versuchen bestimmen. Wir gehen dann
davon aus, dass im Grenzübergang für n gegen ¶ die relative Häufigkeit einem Grenzwert, den wir als Wahrscheinlichkeit dieses Experiments bezeichnen, zustrebt.
Diese verschiedenen Ansätze sind für die Mathematik und rigorose Behandlung nicht geeignet. Die Wahrscheinlichkeitstheorie wurde jedoch mit dem weiter unten behandelten Axiomensystem auf eine feste Grundlage gestellt. Zum
Verständnis des Axiomensystems müssen wir jedoch ein wenig ausholen.
Skript Statistik und Stochastik
11
Ergebnisraum und Ereignisraum
Zufallsexperiment
Wichtige Begriffe im Zusammenhang mit der Wahrscheinlichkeitstheorie sind "Zufallsexperiment", "Ergebnis",
"Elementarereignis", "Ereignis" und "Wahrscheinlichkeit". Diese Terminologie soll in diesem Abschnitt definiert und
erläutert werden.
Ein Zufallsexperiment ist ein Experiment
- mit mehreren (mindestens 2) möglichen Ergebnissen;
- dabei lässt sich nicht sicher voraussagen, welches Ergebnis eintritt;
- die Ergebnismenge ist jedoch festgelegt; d.h. alle potentiell möglichen Ergebnisse sind bekannt;
Bei einem Zufallsexperiment spielt also der Zufall eine wesentliche Rolle.
Beispiele für Zufallsexperimente sind:
† Einmaliges Werfen einer Münze;
† Das Ziehen einer Karte (z.B. aus einem Quartett);
† Die Ziehung der Lottozahlen (6 aus 49);
† 1x Würfeln;
† Gleichzeitiges Werfen eines roten und grünen Würfels;
Die Menge aller möglichen Ergebnisse w eines Zufallsexperiments ist die Ergebnismenge W.
Die Ergebnismenge wird mit dem griechischen Buchstaben W bezeichnet, die einzelnen Ergebnisse allgemein mit dem
kleinen griechischen Buchstaben w.
Die Ergebnismenge
† ist eine nichtleere Menge;
† kann endlich sein: z.B. 81, 2, 3, 4, 5, 6< beim einmaligen Würfeln;
† kann abzählbar unendlich sein; z.B. beim Würfeln bis zum ersten 6-er;
Die Ergebnismengen für die obenstehenden Beispiele von Zufallsexperimenten sind:
† W = 8Kopf, Zahl<
† W = 8Herz As, Herz König, Herz ....<; d.h. die Menge aller Karten
† W = 8 8a, b, c, d, e, f < mit a, b, c, d, e, f œ 81, 2, ... 49< und je zwei nicht gleich <
† W = 8 1, 2, 3, 4, 5, 6 <
† W = 8 81, 1<, 81, 2<, ... 81, 6<, 82, 1<, 82, 2<, ... 86, 6< <
Oft ist man jedoch nicht am genauen Ergebnis w eines Experiments interessiert, sondern an einem allgemeineren
Ereignis. Formal wird ein allgemeineres Ereignis A definiert als Teilmenge des Ergebnisraums. Z.B. könnte im obigen
Experiment "1x Würfeln" das Ereignis "Würfeln einer geraden Zahl" lauten und dieses Ereignis würde der Teilmenge
{2, 4, 6} des Ergebnisraums 8 1, 2, 3, 4, 5, 6 < entsprechen. Ein Ereignis kann also mehrere Ergebnisse umfassen.
Spezielle Ereignisse sind sogenannte Elementarereignisse, die genau einem Ergebnis (z.B. "Würfle eine 6", d.h. 86<)
entsprechen.
12
Skript Statistik und Stochastik
Ein Ereignis A ist eine Teilmenge der Ergebnismenge W.
Die Ergebnismenge W heisst das sichere Ereignis, die leere Menge 8< das unmögliche Ereignis.
Die Elemente w aus W heissen auch Elementarereignisse.
Es gibt sehr viele Ereignisse (z.B. "Gerade Augenzahl würfeln", "2 oder 4 würfeln", "Keine 5 würfeln", etc.) und jedes
Ereignis ist eine Teilmenge des Ergebnisraums.
Für die obenstehenden Zufallsexperimente können wir z.B. folgende Ereignisse A wählen:
† A = 8Kopf<; Kopf wird geworfen;
† A = {Herz As, Karo As, .... As} ; es wird ein As gezogen;
† A = 8 81, b, c, d, e, f < mit b, c, d, e, f œ 81, 2, ... 49< und je zwei nicht gleich <; es wird sicher eine 1 gezogen;
† A = 8 2, 4, 6 <; es wird eine gerade Zahl gewürfelt;
† A = 8 85, 6<, 86, 5<, 86, 6< <; die Summe der Augenzahlen ist grösser als 10;
Der Ereignisraum ist die Menge aller Ereignisse und entspricht zumeist der Potenzmenge (d.h. der Menge aller Teilmengen)
des Ergebnisraums. Der Ereignisraum kann sehr schnell sehr gross werden.
Im Folgenden werden an Hand zweier (leicht komplizierterer) Experimente die Begriffe Ergebnis w, Ergebnisraum W,
Elementarereignis, Ereignis A und Ereignisraum noch etwas ausführlicher behandelt. Man sieht anschaulich, dass
die Grösse des Ereignisraums sehr schnell anwachsen kann.
Illustration: Drei Mal eine Münze Werfen
In diesem Experiment wird drei Mal hintereinander eine Münze geworfen, wobei bei jedem Wurf Kopf (0) oder Zahl
(1) als Ergebnis möglich ist. Bei dreimaligem Würfeln ergibt sich der folgende Ergebnisraum:
880, 0, 0<, 80, 0, 1<, 80, 1, 0<, 80, 1, 1<, 81, 0, 0<, 81, 0, 1<, 81, 1, 0<, 81, 1, 1<<
Der Ergebnisraum W enthält die Ergebnisse bzw. Elementarereignisse {0,0,0}, {0,0,1}, ... und umfasst insgesamt 8
verschiedene Ergebnisse (Elementarereignisse).
Die Anzahl der möglichen Ereignisse (d.h. die Menge aller Teilmengen des Ergebnisraums bzw. die Potenzmenge von
W) ist bereits 256 gemäss der allgemeinen Formel zur Berechnung der Mächtigkeit der Potenzmege von W (
2n = 28 = 256 ), wobei n die Mächtigkeit (Anzahl Elemente) von W ist. Die Begriffe werden in Kürze näher erklärt.
Illustration: Zwei Mal Würfeln
In diesem Experiment wird zwei Mal hintereinander gewürfel, wobei bei jedem Wurf die Augenzahlen 1, 2, 3, 4, 5
oder 6 als Ergebnis möglich sind. Bei zweimaligem Würfeln ergibt sich der folgende Ergebnisraum:
881,
82,
84,
85,
1<,
4<,
1<,
4<,
81,
82,
84,
85,
2<,
5<,
2<,
5<,
81,
82,
84,
85,
3<,
6<,
3<,
6<,
81,
83,
84,
86,
4<,
1<,
4<,
1<,
81,
83,
84,
86,
5<,
2<,
5<,
2<,
81,
83,
84,
86,
6<,
3<,
6<,
3<,
82,
83,
85,
86,
1<,
4<,
1<,
4<,
82,
83,
85,
86,
2<,
5<,
2<,
5<,
82,
83,
85,
86,
3<,
6<,
3<,
6<<
Es gibt also 36 (d.h. 6 mal 6) verschiedene Ergebnisse.
Der Ereignisraum umfasst alle Teilmengen des Ergebnisraums. Diese Menge hat sehr viele Elemente, nämlich 236
oder fast 70 Milliarden (genau: 68719476736).
Skript Statistik und Stochastik
13
Empirisches Gesetz der grossen Zahlen
Das wesentliche Merkmal eines Zufallsexperiments ist, dass wir vor seiner Durchführung nicht wissen, welches der
möglichen Ergebnisse eintreten wird. Für ein bestimmtes Ereignis A können wir nicht mit Sicherheit voraussagen, ob
es eintreten wird oder nicht; es sei denn, A ist entweder das sichere Ereignis W oder das unmögliche Ereignis 8<.
Wir wollen im Folgenden zahlenmässig zu erfassen versuchen, wie "stark" mit dem Eintreten des Ereignisses A zu
rechnen ist. Dazu bietet sich der folgende experimentelle Weg an: wir führen ein Zufallsexperiment mehrfach nacheinander durch und notieren die (sogenannte absolute) Häufigkeit Hn HAL des Auftretens des Ereignisses A bei n-facher
Hn HAL
ÅÅÅÅÅÅ .
Wiederholung sowie die davon abgeleitete relative Häufigkeit hn HAL = ÅÅÅÅÅÅÅÅ
n
Man beobachtet nun im Allgemeinen, dass die relative Häufigkeit mit wachsendem n in der Regel immer weniger um einen
festen Wert schwankt. Dieser sogenannte Stabilisierungseffekt ist eine Erfahrungstatsache und wird das empirische Gesetz der
grossen Zahlen genannt.
Kolmogorov'sches Axiomensystem
Nachdem wir die unbefriedigende Situation mit dem Begriff bzw. der Definition der Wahrscheinlichkeit diskutiert
sowie wichtige Begriffe von Zufallsexperimenten erläutert haben, können wir den axiomatischen Wahrscheinlichkeitsbegriff bzw. den mathematischen Ansatz, die Wahrscheinlichkeitstheorie auf ein Fundament zu stellen, behandeln.
Wir geben im Folgenden das Kolmogorov'sche Axiomensystem (1930er Jahre), die Grundlage der Wahrscheinlichkeitstheorie, wobei W die endliche (oder abzählbar unendliche) Ergebnismenge eines Zufallsexperiments bedeutet.
Ein Wahrscheinlichkeitsraum ist ein Tripel HW, , PL, wobei
W eine nichtleere Menge ist,
eine s-Algebra von Teilmengen von W, d.h.
ist nicht leer,
aus B œ folgt Bc œ und
aus A1 , A2 , ... œ folgt A1 ‹ A2 .... œ , und
P : Ø @0, 1D ist eine Abbildung mit folgenden Eigenschaften:
Axiom1: PHWL = 1
Axiom 2: PHA ‹ BL = PHAL + PHBL für disjunkte Ereignisse A und B
Axiom 3: wie Axiom 2 für eine ¶ Folge von paarweise disjunkten Ereignissen
Die Funktion P : Ø @0, 1D heisst Wahrscheinlichkeitsmass, Wahrscheinlichkeitsabbildung, Wahrscheinlichkeitsverteilung
oder auch kurz Wahrscheinlichkeit.
Wie man leicht einsehen kann, decken sich diese Axiome mit der intuitiven Vorstellung von Wahrscheinlichkeit:
† Gemäss Axiom 1 ist die Wahrscheinlichkeit, irgendein Ergebnis des Ergebnisraums zu erzielen, gleich eins (d.h.
völlige Sicherheit).
† Gemäss Axiom 2 ist die Wahrscheinlichkeit eine 1 oder eine 2 zu würfeln (dies sind disjunkte Ereignisse) gleich
der Summe der Wahrscheinlichkeiten der beiden (Elementar)ereignisse, d.h. ÅÅÅÅ26 .
† Die Wahrscheinlichkeit ist nie grösser als 1 (das sicherer Ereignis) und nie kleiner als 0 (das unmögliche Ereignis).
Eigenschaften von Wahrscheinlichkeitsmassen
In der Praxis ist es oft so, dass die Wahrscheinlichkeit eines Ereignisses nicht direkt ausgerechnet werden kann. Dann
kann man versuchen, das Ereignis als Vereinigung, Durchschnitt, Differenz oder Komplement von Ereignissen, deren
Wahrscheinlichkeit einfacher berechnet werden kann, zu schreiben und die folgenden Beziehungen anzuwenden. Diese
Beziehungen können aus dem Axiomensystem abgeleitet werden:
† PH«L = 0
14
Skript Statistik und Stochastik
† 0 § PHAL § 1
† PHAc L = 1 - PHAL
† A Õ B fl PHB \ AL = PHBL - PHAL
† A Œ B fl PHAL § PHB
† PHB \ AL = PHBL - PHA › BL
† PHA ‹ BL = PHAL + PHBL - PHA › BL
† PHA ‹ BL § PHAL + PHBL
† PHA1 ‹ A2 ‹ ... ‹ An L § ⁄ni=1 PHAi L
In dieser Zusammenstellung sind A und B Ereignisse des Wahrscheinlichkeitsraums HW, , PL und Ac das Komplement von A.
Beispiel 1
Wie gross ist die Wahrscheinlichkeit, beim n-maligen Würfeln wenigstens eine 6 zu würfeln?
Lösung
Das Ereignis "Würfle mindestens eine 6 bei n-maligem Würfeln" ist das Komplement des Ereignisses A "Würfle nur
die Zahlen 1, 2, 3, 4, 5 bei n-maligem Würfeln".
Der Ergebnisraum W beim n-maligen Würfeln hat die Grösse 6n .
Die Anzahl der möglichen Ergebnisse, das Ereignis A zu erzielen (d.h. die Grösse von A), beträgt 5n , da bei jedem
Wurf nur 5 verschiedene Zahlen möglich sind.
Die Wahrscheinlichkeit, das Ereignis A zu erzielen beträgt demnach H ÅÅÅÅ56 L .
n
Die Wahrscheinlichkeit, das Komplement, d.h. beim n-maligen Würfeln wenigstens eine 6 zu würfeln, beträgt demn
nach 1 - H ÅÅÅÅ56 L und strebt für n gegen ¶ gegen 1.
Beispiel 2
In einer Stadt erscheinen zwei Zeitungen A und B. Die Wahrscheinlichkeit, dass ein Einwohner
- die Zeitung A liest sei 60%;
- die Zeitung B liest sei 50%;
- die Zeitung A oder B oder beide liest sei 90%.
Wie gross ist die Wahrscheinlichkeit, dass ein Einwohner
- a. beide Zeitungen liest;
- b. keine der beiden Zeitungen liest;
- c. nur eine der beiden Zeitungen liest.
Lösung
Wenn A das Ereignis ("Lesen der Zeitung A") und B das Ereignis ("Lesen der Zeitung B") bezeichnet, dann gilt:
a. PHA › BL = PHAL + PHBL - PHA ‹ BL = 60 % + 50 % - 90 % = 20 %
êêê êê de Morgan êêêêêêêêê
b. PHA › BL = PHA ‹ BL = 1 - PHA ‹ BL = 100 % - 90 % = 10 %
c. PHA ‹ BL \ PHA › BL = PHA ‹ BL - PHHA › BL › HA ‹ BLL = PHA ‹ BL - PHA › BL = 90 % - 20 % = 70 %
Skript Statistik und Stochastik
15
Venn Diagramme
Mit Hilfe der Venn Diagramme lassen sich die Beziehungen zwischen Ereignissen, die symbolisch oder in Worten
gegeben sind, auch anschaulich graphisch darstellen.
Siehe dazu im Kapitel "Mengenlehre" des Skripts "Abbildungen".
Skript Statistik und Stochastik
16
3. Elementare Kombinatorik
Einleitung
Nachdem wir verschiedene mathematische (mengentheoretische) Beziehungen besprochen haben, möchten wir einen
etwas genaueren Blick auf verschiedene Zufallsexperimente werfen.
Dabei definieren wir zunächst den für unsere Zufallsexperimente wichtigen Begriff des Laplace Experiments, bei dem
jedes Ergebnis mit der gleichen Wahrscheinlichkeit auftritt.
Wichtige Zufallsexperimente sind auch die sogenannten Bernoulli Experimente, bei dem nur zwei Ergebnisse jedoch
mit unterschiedlicher Wahrscheinlichkeit auftreten können, sowie vor allem die mehrstufigen Bernoulli Experimente,
die aus mehreren Bernoulli Experimenten zusammengesetzt sind.
Anschliessend untersuchen wir im Detail sogenannte Urnenexperimente, bei denen aus einer Urne mit n Kugeln k
Kugeln gezogen und die möglichen resultierenden Anordnungen und deren Wahrscheinlichkeiten studiert werden. Es
gibt dabei verschiedene experimentelle Situationen zu berücksichtigen: mit oder ohne Zurücklegen der Kugel, mit oder
ohne Berücksichtigung der Anordnung sowie mit verschiedenen oder teilweise gleichen Kugeln.
Diese Analyse führt uns ins Gebiet der Kombinatorik. Es lassen sich (für Standardsituationen) explizite Formeln
herleiten, die es ermöglichen auf schnelle Art und Weise die möglichen Ergebnisse verschiedener Zufallsexperimente
und deren Wahrscheinlichkeiten anzugeben.
Es wird weiters dargelegt, dass die gleichen Formeln auch für eine andere experimentelle Situation, nämlich der
Aufgabe, k Kugeln auf n Behälter zu verteilen, angewendet werden können. Auch hier gibt es wieder verschiedene (zu
den Urnenexperimenten analoge) experimentelle Situationen.
Für kompliziertere Situationen in der Praxis (vor allem wenn das Experiment zeitabhängige Aspekte enthält) kann oft
nur eine Simulation des Experiments eine Lösung bringen. Es ist jedoch zu beachten, dass bei solchen Zufallsexperimenten die Anzahl der Möglichkeiten sehr schnell ins Unermessliche steigt, und deshalb die ganzen Berechnungen
(aus Zeit- und Memory Überlegungen) idealerweise in (durch Formeln berechenbare) Teile aufgeteilt werden.
Die verschiedenen in diesem Kapitel besprochenen Zufallsexperimente führen in natürlicher Weise auf diskrete
Verteilungen. Die wichtigsten dieser (theoretisch abgeleiteten) Verteilungen und deren Eigenschaften werden jedoch
erst in den folgenden Kapiteln behandelt.
Laplace Experimente
Laplace Wahrscheinlichkeit
In vielen experimentellen Situationen (wie: würfeln, Münze werfen, Karte ziehen etc.) ist jedes Ergebnis mit der
gleichen Wahrscheinlichkeit zu erwarten.
Die Voraussetzung der Gleichwahrscheinlichkeit heisst Laplace-Annahme.
Zufallsexperimente, bei denen die Laplace-Annahme zugrunde gelegt wird, heissen Laplace-Experimente.
Sei W = 8w1 , w2 , ... wn < die endliche Ergebnismenge eines Zufallsexperiments. Dann heisst die Abbildung P mit:
Anzahl der für das Eintreten von A günstigen Fälle
»A»
PHAL = ÅÅÅÅ
ÅÅ Å = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ " A Õ W
»W»
Anzahl der möglichen Fälle
Laplace-Wahrscheinlichkeit.
Skript Statistik und Stochastik
17
Ein Laplace-Experiment geht also von der Annahme aus, dass nur endlich viele Ergebnisse möglich sind und diese alle
die gleiche Wahrscheinlichkeit haben.
Beim Werfen einer Münze ist jedes der Ergebnisse (Kopf, Zahl) mit der gleichen 50% Wahrscheinlichkeit zu erwarten.
Beim Würfeln ist jede Augenzahl (1, 2, 3, 4, 5, 6) mit der gleichen ÅÅÅÅ16 Wahrscheinlichkeit zu erwarten.
Mehrstufige Laplace Experimente - Baumdiagramme
Vorgänge, die sich aus mehreren Teilvorgängen zusammensetzen, heissen mehrstufige Vorgänge (z.B. 5x würfeln).
Den Ablauf eines mehrstufigen Vorgangs kann man oft übersichtlich als Baumdiagramm darstellen. Nach jedem
Teilvorgang verzweigt sich der Baum.
In die Knoten des Baums trägt man in Kreise das bisherige Ergebnis ein. Von jedem Knoten können Äste abzweigen;
die Äste entsprechen den möglichen Ergebnissen des nächsten Teilvorgangs. An jeden Ast schreibt man die Wahrscheinlichkeit, die besteht um von einem Knoten zum nächsten Knoten zu gelangen. Die Summe der Wahrscheinlichkeiten
bei jedem Knoten beträgt 1.
Zu jedem möglichen Ablauf des Gesamtvorgangs gehört ein Weg durch das Baumdiagramm - ein sogenannter Pfad. Es
gibt zwei Pfadregeln:
In einem Baumdiagramm für einen mehrstufigen Vorgang gilt:
Produktregel: Die Wahrscheinlichkeit eines Pfades ist gleich dem Produkt der Wahrscheinlichkeiten entlang dieses Pfades.
Summenregel: Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe der Pfadwahrscheinlichkeiten (d.h. gleich der
Summe der Wahrscheinlichkeiten, die für dieses Ereignis günstig sind).
Bernoulli Experimente
Bei einem Bernoulli Experiment interessiert nur, ob ein Ereignis A eintritt oder nicht. Im ersten Fall spricht man von Erfolg
mit der Wahrscheinlichkeit PHAL = p. Im zweiten Fall spricht man von Misserfolg mit der Wahrscheinlichkeit PHAL = 1 - p.
Wird ein Bernoulli Experiment mehrfach durchgeführt, spricht man von einer Bernoulli Kette.
Bernoulli Formel
In einer Bernoulli Kette der Länge n mit der Erfolgswahrscheinlichkeit p gilt:
n!
PHGenau k ErfolgeL = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ pk H1 - pLn-k k = 0, 1, ... n
k! Hn-kL!
iny
Statt ÅÅÅÅÅÅÅÅ
Ån!ÅÅÅÅÅÅÅÅÅÅÅ wird meist jj zz (sprich: n über k) geschrieben.
k! Hn-kL!
kk{
Mit Hilfe eines Baumdiagramms kann man diese Formel herleiten, bei der der Binomialkoeffizient die Anzahl der
verschiedenen Wege darstellt, die zu dem Ereignis "Genau k Erfolge" führen.
Summenregel
Bei den weiter unten zu besprechenden Urnenexperimenten wird immer wieder auf die Summenregel und die Produktregel zurückgegriffen. Sie werden in diesem und dem nächsten Abschnitt kurz erläutert.
Summenregel: Die Anzahl der Möglichkeiten n, ein Element aus einer von zwei diskunkten Mengen A und B zu wählen, ist
die Summe der Elemente der beiden Mengen: n = n A + nB
Skript Statistik und Stochastik
18
Diese Regel ist unmittelbar einleuchtend. Bei zwei disjunkten Mengen 8a, b, c< und 8d, e< gibt es insgesamt 5 verschiedene Möglichkeiten ein Element zu wählen, nämlich eines aus der Vereinigungsmenge 8a, b, c, d, e<.
Produktregel
Die Anzahl der Möglichkeiten, aus zwei Mengen ein geordnetes Paar zu wählen, ist gleich der Anzahl der Möglichkeiten, das
erste Element zu wählen, multipliziert mit der Anzahl der Möglichkeiten, das zweite Element zu wählen.
Diese Regel ist auch unmittelbar einleuchtend. Jedes Element der ersten Menge kann mit den Elementen der zweiten
Menge gepaart werden. Z.B. bei den zwei Mengen {a,b} und {c,d} gibt es die Ergebnisse {a,c}, {a,d}, {b,c}, {b,d}.
Permutationen und Binomialverteilung
Einleitung
In vielen Fällen ist zur Berechnung von Wahrscheinlichkeiten ein systematisches Abzählen von Mengen wichtig. Die
Kombinatorik ist das Teilgebiet der Mathematik, das sich damit beschäftigt. Fast alle Zufallsexperimente (mit gleichen
Wahrscheinlichkeiten) lassen sich auf die in den nächstenen Abschnitten besprochenen Urnenmodelle zurückführen.
Darin werden Experimente besprochen wo es darum geht, aus einer Urne, die n (verschiedene oder teilweise gleiche)
Kugeln enthält, k Kugeln zu ziehen (mit und ohne Zurücklegen) und zu bestimmen, wieviele verschiedene Konfigurationen (mit oder ohne Berücksichtigung der Anordnung) möglich sind.
Im Folgenden werden verschiedene Begriffe im Zusammenhang mit Listen von nummerierten Kugeln verwendet, die
hier zusammenfassend kurz erklärt und definiert sind:
Kombinatorik
† Geordnet heisst, dass es auf die Reihenfolge der Elemente ankommt.
† Variation heisst geordnet (d.h. die Reihenfolge wird berücksichtigt, z.B. aufeinanderfolgendes Ziehen).
† Kombination heisst nicht geordnet (d.h. Reihenfolge wird nicht berücksichtigt, z.B. gleichzeitiges Ziehen).
† ein k-Tupel ist eine Liste von k Elementen;
† Ein k-Tupel einer Menge mit n Elementen ist eine geordnete Folge von k Elementen, wobei Elemente auch
mehrfach vorkommen können. k-Tupels können auch als Auswahl mit Wiederholungen bzw.Zurücklegen, oder
als Stichproben oder Variationen mit Wiederholungen aufgefasst werden.
† Eine k-Repetition einer Menge mit n Elementen ist eine ungeordnete Auswahl von k Elementen, wobei Elemente auch mehrfach vorkommen können. k-Repetitionen können auch als Kombinationen mit Wiederholungen
bzw. Zurücklegen aufgefasst werden.
† Eine k-Permutation einer Menge mit n (n ≥ kL Elementen ist eine geordnete Auswahl von k paarweise verschiedenen Elementen aus der Menge. Eine n-Permutation wird auch einfach Permutation genannt. k-Permutationen können auch als Auswahl ohne Wiederholungen bzw. Zurücklegen, oder als Stichproben oder Variationen
ohne Wiederholungen aufgefasst werden.
† Eine k-Kombination einer Menge mit n (n ≥ kL Elementen ist eine ungeordnete Auswahl von k paarweise
verschiedenen Elementen aus der Menge. k-Kombinationen können auch als ungeordnete Auswahl ohne Wiederholungen bzw. Zurücklegen, oder als Kombination ohne Wiederholungen aufgefasst werden.
† n! (gesprochen: n Fakultät) entspricht dem Produkt 1 ä2 ä ... ä n.
Skript Statistik und Stochastik
19
Mengenlehre
† Beachten Sie, dass es bei Mengen auf die Reihenfolge ihrer Elemente nicht ankommt.
† Die Mächtigkeit einer Menge gibt die Anzahl ihrer Elemente an.
† Die Potenzmenge einer Menge ist die Menge aller Teilmengen dieser Menge. Wenn die Menge n Elemente hat, so
hat die Potenzmenge 2n Elemente.
† Begriffe: Vereinigungsmenge, Durchschnittsmenge, Komplementärmenge (Komplement).
Bevor wir diese allgemeinen Urnenexperimente untersuchen, soll jedoch noch auf wichtige Spezialfälle (mit k = n)
eingegangen werden.
Ohne Zurücklegen - alle verschieden
Es gibt n ! mögliche Anordnungen (Variationen), wenn n Kugeln aus einer Urne mit n verschiedenen Kugeln gezogen werden
(ohne Zurücklegen und mit Berücksichtigung der Reihenfolge). Es gibt nur eine Kombination.
Bei der ersten Kugel gibt es n Möglichkeiten, bei der zweiten nur noch (n - 1), etc. bis 1: d.h. die Anzahl der Möglichkeiten ist: n Hn - 1L Hn - 2L ... 2 1 = n!
Zur Angabe dieser Anzahl wurde eine neue Funktion (Fakultät bzw.!) definiert: es gilt
n ! = 1 ä2 ä ... ä n
Die Anzahl der Kombinationen, bei denen es auf die Reihenfolge nicht ankommt, ist gleich 1, da alle Anordnungen
(Variationen) die gleichen Elemente enthalten, nämlich alle n (verschiedenen) Kugeln.
Beispiel
Gegeben sei die Menge 8a, b, c<.
Es gibt die folgenden 3 ! = 6 Permutationen (Variationen): 88a, b, c<, 8a, c, b<, 8b, a, c<, 8b, c, a<, 8c, a, b<, 8c, b, a<<
Es gibt nur eine Kombination: 88a, b, c<<
Ohne Zurücklegen - mehrere Klassen
n!
Es gibt ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅ verschiedene Möglichkeiten n Kugeln, die in m Klassen von je ki Hi = 1, .. mL nicht unterscheidbaren Kugeln
k1 ! k2 ! ... km !
eingeteilt werden können (und ⁄m
i=1 ki = n gilt), anzuordnen.
Es gibt n ! Möglichkeiten n Kugeln anzuordnen. Jede nichtunterscheidbare Art (z.B. Farbe rot) kann auf ki ! verschiedene Arten angeordnet werden, ohne dass man an der Darstellung einen Unterschied bemerkt. Man muss also
durch alle diese ki ! teilen.
n!
10!
Beispiel: 3 blaue und 7 rote Kugeln können auf ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅ = 120 verschiedene Arten angeordnet werden.
k1 ! k2 !
3! 7!
Ohne Zurücklegen - mit 2 Klassen
Ein wichtiger Spezialfall der vorherigen Situation ist der Fall, wenn zwei Klassen (d.h. m = 2) vorhanden sind.
20
Skript Statistik und Stochastik
n!
n!
Es gibt ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ verschiedene Möglichkeiten n Kugeln, die in 2 Klassen mit Häufigkeit k bzw. n - k eingeteilt werden
k1 ! k2 !
k! Hn-kL!
können, anzuordnen.
i 10 y
10!
Beispiel: Wir können das vorherige Beispiel verwenden und erhalten wiederum jj zz = ÅÅÅÅÅÅÅÅ
ÅÅÅ = 120 .
k 3 { 3! 7!
Urnenexperimente bei verschiedenen Elementen
Urnenexperimente
In diesem Kapitel werden wir zunächst eine Urne mit n verschiedenen (z.B. von 1 bis n durchnummerierten) Kugeln
betrachten und wir ziehen zufällig k-mal nacheinander eine Kugel aus der Urne. Die möglichen Ergebnisse und die
Mächtigkeit des Ergebnisraumes hängen dabei entscheidend von der Art der Ziehung ab.
Es kann die Reihenfolge der gezogenen Elemente berücksichtigt werden (man spricht dann von Variation oder geordneter Liste) oder nicht (man spricht dann von Kombination oder ungeordneter Liste). Die Anzahl der Variationen ist
grösser als die (oder gleich der) Anzahl der Kombinationen. Dementsprechend ist die Wahrscheinlichkeit, ein bestimmtes Ergebnis zu erzielen, bei der Variation kleiner als die (oder gleich der) Wahrscheinlichkeit bei der entsprechenden Kombination.
Bei einer Variation muss notwendigerweise nacheinander gezogen werden, bei einer Kombination könnte auch
gleichzeitig gezogen werden.
Beispiel: Bei der Variation unterscheidet man zwischen den Ergebnissen 82, 4, 8< und 84, 8, 2<, bei der Kombination
werden sie jedoch als das gleiche Ergebnis betrachtet.
Eine weitere Unterscheidung besteht darin, ob nach dem Ziehen der Kugel die Kugel zurückgelegt wird oder nicht.
Dies führt auf die Unterscheidung mit / ohne Zurücklegen. Wenn alle Elemente verschieden sind, hat man im zweiten
Fall auch im Ergebnis nur unterschiedliche Kugeln.
Diese zwei Unterscheidungen (Variation oder Kombination, mit oder ohne Zurücklegen) führen auf insgesamt 4
verschiedene experimentelle Situationen, die in diesem Kapitel genauer behandelt werden. In einem späteren Abschnitt
wird ausserdem noch die Unterscheidung gemacht, ob alle Kugeln unterschiedlich sind oder nicht. Dies führt auf
weitere unterschiedliche experimentelle Situationen.
Mit Zurücklegen und Geordnet (k-Tupel)
Experiment: Aus einer Urne mit n verschiedenen Kugeln werden k Kugeln ausgewählt. Nach jedem Zug wird die Kugel
wieder zurückgelegt. Jede unterschiedliche Anordnung von k Kugeln wird gezählt.
Anzahl Möglichkeiten:
nk = ´¨¨¨¨
n ¨¨¨≠...¨¨¨¨¨nÆ
k-mal
Es gibt nk k-Tupel, da es n Möglichkeiten zur Wahl des ersten Elements der Folge, n Möglichkeiten zur Wahl des
zweiten Elements der Folge, etc. ... gibt. Jede Möglichkeit tritt mit der Wahrscheinlichkeit ÅÅÅÅ1n auf, jedes k-Tupel tritt
mit der gleichen Wahrscheinlichkeit H ÅÅÅÅ1n L auf.
k
Beispiel
Gegeben sei die Menge 8a, b, c<.
21
Skript Statistik und Stochastik
Es gibt die folgenden nk = 32 = 8 Möglichkeiten, aus der Menge mit n = 3 Elementen k = 2 Elemente zu ziehen:
88a, a<, 8a, b<, 8a, c<, 8b, a<, 8b, b<, 8b, c<, 8c, a<, 8c, b<, 8c, c<<
Mit Zurücklegen und Ungeordnet (k-Repetition)
Experiment: Aus einer Urne mit n verschiedenen Kugeln werden k Kugeln ausgewählt. Nach jedem Zug wird die Kugel
wieder zurückgelegt. Von Tupels, die die gleichen Elemente enthalten, wird nur eines gezählt.
Anzahl Möglichkeiten:
ij n + k - 1 yz
j
z
k
k
{
Diese Herleitung ist ein wenig komplizierter. Wir können jedoch folgende Überlegung anstellen.
Da die Reihenfolge nicht interessiert, können wir eine Strichliste anlegen: d.h. wir schreiben der Reihe nach für jede
der n Kugeln Striche entsprechend der Anzahl mit der diese Kugel gezogen wurde und trennen diese Gruppe von
Strichen für benachbarte n jeweils durch ein Trennzeichen. Wir haben also insgesamt k Striche plus n - 1 Trennzeichen, die wir auf Hn + k - 1L ! verschiedene Arten anordnen können. Da jedoch die Striche und Zwischenräume nicht
unterscheidbar sind, müssen wir diese Anzahl durch k ! und Hn - 1L! teilen und erhalten als Ergebnis
i k + n - 1 yz
Hk+n-1L!
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅ = jj
z.
k! Hn-1L!
k
k
{
Beispiel
Gegeben sei die Menge 8a, b, c<.
Hk+n-1L!
4!
Es gibt die folgenden ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅ = 6 Möglichkeiten, aus der Menge mit n = 3 Elementen k = 2 Elemente zu
2! 2!
k! Hn-1L!
ziehen:
88a, a<, 8a, b<, 8a, c<, 8b, b<, 8b, c<, 8c, c<<
Ohne Zurücklegen und Geordnet (k-Permutation)
Experiment: Aus einer Urne mit n verschiedenen Kugeln werden k Kugeln ausgewählt. Nach jedem Zug wird die Kugel nicht
wieder zurückgelegt. Jede unterschiedliche Anordnung von k Kugeln wird gezählt.
Anzahl Möglichkeiten:
n!
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ = n´¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨
Hn - 1L
...¨¨≠Hn
- k +¨¨¨¨1L
¨¨¨¨¨¨¨¨
¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨
¨¨¨¨Æ
Hn-kL!
k-mal
n!
Es gibt ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ k-Permutationen, da es n Möglichkeiten zur Wahl des ersten Element der Folge, (n - 1) Möglichkeiten
Hn-kL!
n!
zur Wahl des zweiten Elements, etc. ... gibt, also: n Hn - 1L ... Hn - k + 1L = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ .
Hn-kL!
Spezialfall k = n
Es gibt n ! n-Permutationen bzw. Permutationen. Beim ersten Ziehen gibt es n Möglichkeiten, beim zweiten n - 1, etc.
.... und schliesslich beim letzten Zug eine Möglichkeit. Die Totalanzahl der Möglichkeiten beträgt demnach
n Hn - 1L ... 1 = n !
Beispiel
Gegeben sei die Menge 8a, b, c<.
22
Skript Statistik und Stochastik
3!
n!
Es gibt die folgenden ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = ÅÅÅÅ
ÅÅ = 6 Möglichkeiten, aus der Menge mit n = 3 Elementen k = 2 Elemente zu ziehen:
Hn-kL!
1!
88a, b<, 8b, a<, 8a, c<, 8c, a<, 8b, c<, 8c, b<<
Ohne Zurücklegen und Ungeordnet (k-Kombinationen)
Experiment: Aus einer Urne mit n verschiedenen Kugeln werden k Kugeln ausgewählt. Nach jedem Zug wird die Kugel nicht
wieder zurückgelegt. Von Tupels, die die gleichen Elemente enthalten, wird nur eines gezählt.
Anzahl Möglichkeiten:
n!
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ
k! Hn-kL!
n!
Es gibt ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ k-Kombinationen, da jeweils k ! k-Permutationen zu einer k-Kombination zusammengefasst werden
k! Hn-kL!
können.
Beispiel
Gegeben sei die Menge 8a, b, c<.
3!
Es gibt die folgenden ÅÅÅÅÅÅÅÅ
Ån!ÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅ = 3 Möglichkeiten, aus der Menge mit n = 3 Elementen k = 2 Elemente zu
k! Hn-kL!
2! 1!
ziehen:
88a, b<, 8a, c<, 8b, c<<
Zusammenfassung - Ziehen mit verschiedenen Elementen
In den vorigen Abschnitten wurden die möglichen Anordnungen von k Elementen aus einer Menge bzw. Liste mit n
verschiedenen Elementen diskutiert.
Übersichtsweise kann dies folgendermassen zusammengefasst werden:
Variation
HgeordnetL
Kombination
HungeordnetL
mit Zurücklegen ohne Zurücklegen
HmehrfachL
HverschiedenL
nk
J
n+k−1
N
k
n!
Hn−kL!
J
n
N
k
Bei der Benutzung dieser Tabelle ist zu berücksichtigen, dass diese expliziten Formeln gelten, wenn alle Elemente im
Ausgangstopf verschieden sind.
Verteilungen in Behälter
In den bisherigen Experimenten hatten wir n verschiedene Kugeln in einer Urne und haben die Anzahl Möglichkeiten
berechnet, k Kugeln daraus zu entnehmen und anzuordnen.
Die Anzahl der möglichen Anordnungen ergab sich dabei z.B. beim Fall mit Zurücklegen und unter Berücksichtigung
der Reihenfolge zu:
23
Skript Statistik und Stochastik
W = {w » w = (a1 , a2 , ... ak ), ai = 1, ... n}
wobei hier ai die Nummer (von 1 bis n) der i-ten gezogenen Kugel angibt.
Nun betrachten wir ein anderes Experiment, und zwar sollen k Kugeln auf n Behälter verteilt werden. Die Anzahl der
möglichen Verteilungen ist nun z.B. für den Fall mit Mehrfachbelegung und unterscheidbaren Objekten gleich:
W = {w » w = (a1 , a2 , ... ak ),
ai = 1, ... n}
wobei hier ai für jede Kugel mit der Nummer i den Behälter (von 1 bis n) angibt.
Es ist nun bemerkenswert, dass beide Experimente die gleichen Formeln liefern. Aber Achtung: die Anzahl der Kugeln ist im
ersten Fall gleich n, im zweiten Fall gleich k.
Die Tatsache, dass die gleichen Formeln angewandt werden können, gilt nicht nur für den betrachteten Fall (mit
Zurücklegen und unter Berücksichtigung der Anordnung), sondern in allen vier Fällen, wenn folgende Zuordnung
gemacht wird:
Experiment Anordnungen Experiment Verteilungen
n Kugeln
k Kugeln
davon k Kugeln ziehen
auf n Behälter verteilen
mit Zurücklegen
mit Mehrfachbelegung
ohne Zurücklegen
mit Einfachbelegung
mit Berücksichtigung der Reihenfolge
unterscheidbare Objekte
ohne Berücksichtigung der Reihenfolge
nicht unterscheidbare Objekte
Beispiel
Auf wieviele Arten können die (unterscheibaren) Objekte {a,b} auf drei Behälter mit Einfachbelegung verteilt werden?
n!
3!
ÅÅÅÅÅÅ = ÅÅÅÅ
ÅÅ = 6
† Die Formel lautet (k Kugeln und n Behälter): ÅÅÅÅÅÅÅÅ
Hn-kL!
1!
† Die Lösung lautet: auf 6 verschiedene Arten, nämlich {a,b,-}, {a,-,b}, {b,a,-}, {-,a,b}, {b,-,a}, {-,b,a}
Der analoge Fall wäre: auf wieviele Arten können zwei Objekte aus einer Urne mit den drei Objekten {a,b,c} gezogen
und angeordnet werden (ohne Zurücklegen und unter Berückischtigung der Anordnung).
n!
3!
† Die Formel lautet (n Kugeln und k-mal Ziehen): ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = ÅÅÅÅ
Å =6
Hn-kL!
1!
† Die Lösung lautet: auf 6 verschiedene Arten, nämlich {a,b}, {a,c}, {b,a}, {b,c}, {c,a}, {c,b}
Urnenexperimente bei teilweise gleichen Elementen
Einleitung
Bie den bisherigen Urnenexperimenten wurde immer (mit Ausnahme des Abschnitts "Permutationen und Binomialverteilung") vorausgesetzt, dass sich im Topf, aus dem die Elemente gezogen werden, nur unterschiedliche Elemente
befinden. Wir haben die folgenden 22 Fälle unterschieden:
† Erstens kann nach dem Ziehen die Kugel zurückgelegt werden oder auch nicht (mit anderen Worten Wiederholung ist erlaubt oder auch nicht). Wenn die Kugel zurückgelegt wird, ändert sich die Wahrscheinlichkeit für das
Ziehen jeder Kugel nicht, andernfalls schon.
24
Skript Statistik und Stochastik
† Zweitens kann es auf die Reihenfolge der gezogenen Kugeln ankommen (Variation) oder auch nicht (Kombination). Eine Variation kann durch aufeinanderfolgendes Ziehen, eine Kombination durch gleichzeitiges Ziehen
simuliert werden.
Im Folgenden wird nun eine neue experimentelle Situation untersucht, nämlich ...
† Drittens können alle Kugeln verschieden sein oder es können einzelne Kugeln gleich sein (z.B. gleiche Nummer
oder gleiche Farbe). Wenn einzelne Kugeln gleich sind, können sie in Kategorien oder Klassen zusammengefasst
werden.
... womit nun insgesamt 23 Fälle zu unterscheiden sind.
Dies ermöglicht neue Fragestellungen: z.B. auf wie viele Arten können (mit Zurücklegen) drei rote Kugeln gezogen
werden, wenn sich im Topf zwei rote und drei blaue Kugeln befinden?
Allgemeiner formuliert haben wir nun n Kugeln, die in m verschiedene Klassen zusammengefasst werden können und
ni die Anzahl der Kugeln in jeder Klasse angibt, wobei gilt: ⁄m
i=1 ni = n.
Es kann jetzt schon vorausgesagt werden, dass dann die oben hergeleiteten Formeln für die Anzahl der Auswahlen
nicht mehr gelten bzw. in der Bedeutung der Variablen angepasst werden müssen.
Auf diese Formeln wird im Weiteren näher angegangen.
Für die Zahl der möglichen Anordnungen von Objekten aus mehreren Klassen, die untereinander jeweils innerhalb
einer Klasse nicht unterscheidbar sind, ist es hilfreich, zunächst die mögliche Zahl der Anordnungen der Objekte zu
betrachten und dann zu überlegen, wieviele dieser Anordnungen nicht unterscheidbar sind. Die Zahl der möglichen
Anordnungen bei unterscheidbaren Objekten wird dann durch die Zahl der nicht unterscheidbaren Anordnungen
dividiert.
Ziehen mit Zurücklegen - Variationen und Kombinationen
Experiment
Aus einer Urne mit n (teilweise gleichen) Kugeln, die in m Kategorien eingeteilt werden können, werden k Kugeln ausgewählt.
Nach jedem Zug wird die Kugel wieder zurückgelegt.
Anzahl Variatonen
mk
Anzahl Kombinationen
ij m + k - 1 yz
j
z
k
k
{
Beim ersten Zug haben wir m Möglichkeiten (die Wahrscheinlichkeit, dass eine Kugel einer bestimmten Klasse
gezogen wird, hängt natürlich von der Grösse der Klasse ab), ebenso beim zweiten, ... bis zum k-ten Zug. Dies liefert
mk verschiedene Variationen.
Die Herleitung der Formel für die Anzahl Kombinationen geht analog zum Fall der unterscheidbaren Kugeln, nur muss
auch hier n (die Anzahl der Kugeln) durch m (die Anzahl der Kategorien) ersetzt werden.
Beispiel
Gegeben sei die Liste folgender Elemente (keine Menge!): l = 8a, b, b, c<
Es gibt die folgenden mk = 32 = 9 Möglichkeiten, aus der Menge mit m = 3 Kategorien k = 2 geordnete Elemente zu
ziehen:
88a, a<, 8a, b<, 8a, c<, 8b, a<, 8b, b<, 8b, c<, 8c, a<, 8c, b<, 8c, c<<
25
Skript Statistik und Stochastik
Beispiel
Gegeben sei die Liste folgender Elemente (keine Menge!): l = 8a, b, b, c<
i m + k - 1 yz ij 4 yz
Es gibt die folgenden jj
z = j z = 6 Möglichkeiten, aus der Menge mit m = 3 Kategorien k = 2 ungeordnete
k
k
{ k2{
Elemente zu ziehen:
88a, a<, 8a, b<, 8a, c<, 8b, b<, 8b, c<, 8c, c<<
Ziehen ohne Zurücklegen - Variation und Kombination
Experiment
Aus einer Urne mit n (teilweise gleichen) Kugeln, die in m Kategorien eingeteilt werden können, werden k Kugeln ausgewählt.
Nach jedem Zug wird die Kugel nicht wieder zurückgelegt.
Anzahl Variatonen
keine Formel verfügbar
Anzahl Kombinationen
keine Formel verfügbar
Beispiel
Gegeben sei die Liste folgender Elemente (keine Menge!): l = 8a, b, b, b<
Es gibt die folgenden 3 Möglichkeiten, aus der Menge mit m = 2 Kategorien k = 2 geordnete Elemente zu ziehen:
88a, b<, 8b, a<, 8b, b<<
Beispiel
Gegeben sei die Liste folgender Elemente (keine Menge!): l = 8a, b, b, b<
Es gibt die folgenden 2 Möglichkeiten, aus der Menge mit m = 2 Kategorien k = 2 ungeordnete Elemente zu ziehen:
88a, b<, 8b, b<<
26
Skript Statistik und Stochastik
4. Bedingte Wahrscheinlichkeiten
Einleitung
Bislang haben wir uns mit Fragestellungen wie ...
† "Wie gross ist die Wahrscheinlichkeit, dass bei zweimaligem Würfeln eine Summe grösser als 9 gewürfelt wird?".
... beschäftigt.
In diesem Kapitel sollen nun Fragen der folgenden Art untersucht werden:
† "Wie gross ist die Wahrscheinlichkeit, dass bei zweimaligem Würfeln eine Summe grösser als 9 gewürfel wird,
wenn wir beim ersten Wurf keine 6 erreicht haben?".
Es wird nun also nach der Wahrscheinlichkeit eines Ereignisses gesucht, wenn Zusatzinformationen vorhanden sind,
die den Ergebnisraum einschränken. Die Wahrscheinlichkeit des Ereignisses wird damit nicht mehr in Bezug zur
Mächtigkeit des ganzen Ergebnisraums gesetzt, sondern in Bezug zu einer Teilmenge des Ergebnisraums.
Bedingte Wahrscheinlichkeit
Dies führt uns auf folgende Definition:
Gegeben sei ein diskreter Wahrscheinlichkeitsraum HW, , PL und zwei beliebige Ereignisse A und B mit PHBL > 0. Dann
heisst
PHA › BL
PHA » BL = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
PHBL
die bedingte Wahrscheinlichkeit von A unter der Bedingung B. (oder lies: P von A unter der Bedingung B). Die bedingte
Wahrscheinlichkeit PHA » BL gibt die Wahrscheinlichkeit für das Eintreten von A an, wenn die Teilinformation "B ist
eingetreten" vorliegt.
Statt PHA » BL schreibt man auch PB HAL.
Beachte: Die bedingte Wahrscheinlichkeit PHA » BL wird leicht mit der Wahrscheinlichkeit des Durchschnitts
PHA › BL verwechselt.
Beispiel 1: wie gross ist die Wahrscheinlichkeit, dass eine 1 gewürfelt wurde, wenn wir wissen, dass eine ungerade
P HA › BL
1ê6
1
Zahl gewürfelt wurde? Die Antwort lautet nun P HA » BL = = P HBL
1ê2 = 3 , da der Ausgang (würfle eine 1)
zu den drei möglichen Ausgängen (1, 3, 5) in Beziehung gesetzt werden muss.
Beispiel 2: wie gross ist die Wahrscheinlichkeit, dass eine 2 gewürfelt wurde, wenn wir wissen, dass eine ungerade
Zahl gewürfelt wurde? Die Antwort lautet nun 0, da der Ausgang (würfle eine 2) nicht möglich ist (2 ist keine
ungerade Zahl, bzw. A › B = {} ).
Mit obigen Definitionen lassen sich (relativ einfach) verschiedene Formeln herleiten.
Für zwei Ereignisse A und B mit PHBL > 0 gilt:
Multiplikationsformel:
PHB »AL PHAL
PHA » BL = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ
PHBL
PHA › BL = PHA » BL PHBL
Allgemeine Multiplikationsformel:
PHAn » A1 › ... › An-1 L
PHA1 › A1 › ... › An L = PHA1 L PHA2 » A1 L PHA3 » A1 › A2 L ...
27
Skript Statistik und Stochastik
Für den Fall, dass die Ereignisse A1 , A2 ... An eine Partition von W ergeben (d.h. sie schliessen sich gegenseitig aus
und ihre Vereinigung ergibt W), gelten weiter die beiden Formeln:
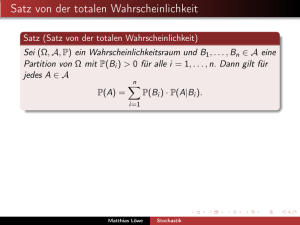
PHBL = ⁄ni=1 PHB » Ai L PHAi L
Formel von der totalen Wahrscheinlichkeit:
Formel von Bayes:
PHB »Ak L PHAk L
PHAk » BL = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ
⁄n PHB »A L PHA L
i=1
i
i
Beispiel
Zwei Laplace-Würfel, ein grüner und ein roter, werden einmal gleichzeitig geworfen.
Frage 1: Wie groß ist die Wahrscheinlichkeit, dass die Augensumme beider Spielwürfel grösser als 9 ist?
Antwort 1: Sei A das Ereignis „die Augensumme ist grösser als 9“. Dann ergibt sich wegen
A = 8H4, 6L, H6, 4L, H5, 5L, H5, 6L, H6, 5L, H6, 6L<,
»A» = 6
und
» W » = 36 die
Wahrscheinlichkeit
PHAL = 6 ê 36 = 1 ê 6.
Frage 2: Wie groß ist die Wahrscheinlichkeit, dass die Augensumme beider Spielwürfel grösser als 9 ist, wenn man
schon weiss, dass der grüne Würfel keine „6“ zeigt?
Antwort 2: Die Bedingung B „der grüne Würfel zeigt keine 6“ reduziert die Anzahl der möglichen Fälle von 36 auf
30, da nur noch die Fälle betrachtet werden, bei denen der grüne Würfel 1, 2, 3, 4 oder 5 zeigt. Von diesen 30 Fällen
sind 3 Fälle günstig, nämlich HA, BL aus 8H4, 6L, H5, 5L, H5, 6L<. Also ist die gesuchte Wahrscheinlichkeit
3 ê 30 = 1 ê 10.
Stochastische Unabhängigkeit
Die bedingte Wahrscheinlichkeit PHA » BL gibt die Wahrscheinlichkeit für das Eintreten von A an, wenn die Teilinformation "B ist eingetreten" vorliegt.
Zwei Ereignisse sind stochastisch unabhängig, wenn das Eintreten von B nichts an der Wahrscheinlichkeit für das Eintreten
von A ändert, wenn also gilt: PHA » BL = PHAL
Ereignisse, die nicht stochastisch unabhängig sind, bezeichnet man als stochastisch abhängig.
Für stochastisch unabhängige Ereignisse vereinfachen sich die im vorigen Abschnitt angegebenen Multiplikationsformeln.
In einem diskreten Wahrscheinlichkeitsraum (W, , P) heissen zwei Ereignisse A und B stochastisch unabhängig, wenn für
sie die Produktformel gilt: PHA › BL = PHAL PHBL
Skript Statistik und Stochastik
28
5. Zufallszahlengenerator
Einleitung
Bei der Simulation eines Zufallsexperiments muss jedes Ergebnis als zufällig betrachtet werden.
Es gibt verschiedene Geräte um Zufallszahlen zu erzeugen:
† ein Münzwurf liefert die beiden Zufallszahlen 0 und 1;
† ein Würfel liefert die sechs Zufallszahlen 1 bis 6;
† eine Urne mit n (von 1 bis n nummerierten Kugeln) liefert die n Zufallszahlen 1 bis n;
† Glücksräder mit n Einstellungen liefern Zufallszahlen 1 bis n;
Ausserdem können Computer (Quasi)-Zufallszahlen liefern. Sie sind nicht zufällig, sondern deterministisch, da sie
nach einem bestimmten Algorithmus berechnet werden. Sie haben auch die nützliche Eigenschaft, dass sie durch das
Setzen eines Startwerts (seed) immer wieder die gleiche Sequenz liefern.
Diese vom Zufallszahlengenerator gelieferten Zahlen können diskret oder (quasi)stetig sein. Sie können auch gleichmässig verteilt sein oder eine bestimmte Verteilung aufweisen.
In Mathematica können ...
† die Funktion Random: Random[] liefert eine reelle Zufallszahl mit gleichmässiger Verteilung im Intervall [0,1].
Mit Argumenten können Werte mit diskreten oder anderen stetigen Verteilungen retourniert werden.
† die Funktion SeedRandom[...]: damit lässt sich der Zufallszahlengenerator zurücksetzen (reset);
† die Variable $RandomState: diese Variable enthält den aktuellen Zustand des Zufallszahlengenerators (d.h. eine
grosse Integer Zahl);
... verwendet werden.
Auch Excel liefert Möglichkeiten (wenn auch bei weitem nicht so komfortable wie Mathematica), Zufallszahlen zu
erzeugen.
29
Skript Statistik und Stochastik
6. Zufallsvariablen und ihre Verteilungen
Einleitung
In den bisherigen Kapiteln haben wir uns vor allem mit Urnenexperimenten und der Anzahl der verschiedenen Ergebnisse und Ereignisse beschäftigt. Wenn die Anzahl der Ereignisse durch die Mächtigkeit des Ergebnisraums geteilt
wird, erhalten wir eine (auf @0, 1D normierte) Wahrscheinlichkeit für das Ereignis.
In diesem Kapitel werden wir uns zunächst weiterhin mit diskreten Verteilungen beschäftigen. Bei den diskreten
Verteilungen gibt es für jedes Ereignis A eine bestimmte Wahrscheinlichkeit pHAL. Wir werden lernen, wie solche
Verteilungen mit wenigen Masszahlen beschrieben werden können.
Anschliessend werden wir uns mit stetigen Verteilungen beschäftigen. In dieser Situation wird der Definitionsbereich
der Verteilungsfunktion als (quasi)stetig vorausgesetzt. Dies kann auf zwei verschiedene Arten geschehen.
Erstens kann dies als Grenzübergang verstanden werden, wenn für eine grosse Anzahl von Versuchen der Definitionsbereich der Verteilung immer grösser wird und die Verteilung immer mehr gegen eine Normalverteilung strebt.
Beispielsweise resultiert bei der Binomialverteilung für grosse n annähernd eine (stetige) Normalverteilung wie das
folgende Beispiel (mit n = 1000 und k = 0.5) zeigt:
0.025
0.02
0.015
0.01
0.005
450
500
550
Wir werden einige Beispiele für solche Übergänge im Abschnitt "Zentraler Grenzwertsatz" kennen lernen.
Zweitens kann (im Unterschied zu unseren Urnenexperimenten) das Ergebnis einer Messung (z.B. eine Temperaturmessung) kontinuierliche Werte annehmen. Z.B. zeigt das folgende Beispiel eine Normalverteilung mit dem Mittelwert
60.34 und Standardabweichung 2.56:
0.15
0.125
0.1
0.075
0.05
0.025
50
60
70
80
Wir messen also stetig verteilte Werte, die wir zur optimalen Darstellung als Histogramm in Kategorien einteilen
können. Bei den diskreten Verteilungen ist pHxL die Wahrscheinlichkeit. Bei den stetigen Verteilungen ist pHxL die
Wahrscheinlichkeitsdichte, und die Wahrscheinlichkeit für das Ereignis (dass sich der Messwert im Intervall
Skript Statistik und Stochastik
30
@a, a + dxD befindet), ergibt sich aus der Multiplikation von pHxL mit der Breite des Intervalls dx. Die Wahrscheinlichkeit ist also durch die Fläche unter der Wahrscheinlichkeitsdichtekurve gegeben.
Die Wahrscheinlichkeit ist also im diskreten Fall durch pHxL, im stetigen Fall durch die Fläche unter der pHxL Kurve,
b
d.h. Ÿa pHxL „ x, gegeben.
Die beiden ganz zentralen (Mathematica) Funktionen im Zusammenhang mit Verteilungen sind die
† PDF (probability density function, Wahrscheinlichkeitsfunktion), d.h.die Wahrscheinlichkeit bei diskreten Verteilungen bzw. die Wahrscheinlichkeitsdichte bei stetigen Verteilungen; sowie die
† CDF (cumulative probability density function, Verteilungsfunktion), d.h. die kumulierte Wahrscheinlichkeit bzw.
Wahrscheinlichkeitsdichte;
Bei diskreten Verteilungen (bei denen die Abszissenwerte der Grösse nach geordnet werden können) und bei
stetigen Verteilungen gibt die CFD(x) die Wahrscheinlichkeit an, dass der Messwert § x beträgt. Bei diskreten
Verteilungen entspricht die CDF einer Summe über die Wahrscheinlichkeiten für Messwerte b x, bei stetigen
Verteilungen einem Integral von -¶ bis x.
Wir werden im nächsten Abschnitt noch genauer auf die PDF und CDF eingehen.
Bei der Behandlung der verschiedenen Verteilungen in den nächsten Abschnitten werden wir immer wieder eine kleine
Tabelle mit wichtigen Eigenschaften von Verteilungen wie dem Träger (Domain), der PDF, der CDF , dem arithmetischen Mittelwert (Mean) sowie der Varianz (Variance) darstellen. Andere wichtige Eigenschaften und Masszahlen von
Verteilungen (und empirischen Daten) werden wir im Kapitel "Deskriptive Statistik" kennenlernen.
PDF und CDF
Werte der PDF und CDF sind in vielen Lehrbüchern tabelliert. Mit den Möglichkeiten des Computers und den in diesem
Abschnitt besprochen Funktionen können wir auf solche Tabellen jedoch verzichten.
Im Folgenden werden die Ausführungen mit den Mathematica Funktionen PDF, CDF und Quantile (Quantilsfunktion)
durchgeführt. Man könnte das Gleiche auch mit den entsprechenden Funktionen anderer Softwarepakete
demonstrieren.
Mit Hilfe der PDF lassen sich sehr einfach Wahrscheinlichkeiten (bei diskreten Verteilungen) bzw. Wahrscheinlichkeitsdichten (bei stetigen Verteilungen) berechnen. Wenn der PDF oder der CDF eine bestimmte Verteilung als erstes
Argument übergeben wird (z.B. "PDFHNormalDistributionH5, 1L, xL" für eine Normalverteilung mit Mittelwert 5 und
Standardabweichung 1) ...
pdfHx_L := PDFHNormalDistributionH5, 1L, xL;
cdfHx_L := CDFHNormalDistributionH5, 1L, xL;
quantileHx_L := QuantileHNormalDistributionH5, 1L, xL;
... dann geben diese Funktionen die Wahrscheinlichkeitsdichte, die Verteilung oder die Quantilsfunktion für diese
Verteilung an der Stelle x zurück.Mit diesen Funktionen lassen sich auch die Wahrscheinlichkeitsdichte (PDF) ...
Plot@pdfHxL, 8x, 0, 10<, PlotRange Ø AllD;
31
Skript Statistik und Stochastik
0.4
0.3
0.2
0.1
2
4
6
8
10
... oder die Verteilung (CDF), die die Wahrscheinlichkeit angibt, dass der Messwert § x beträgt graphisch darstellen:
Plot@cdf@xD, 8x, 0, 10<, PlotRange Ø AllD;
1
0.8
0.6
0.4
0.2
2
4
6
8
10
An Stelle der obigen Normalverteilung hätten wir auch eine andere Verteilung nehmen können, um die wesentlichen
Eigenschaften zu diskutieren.
Wie schon ausgeführt gibt die pdf(x) bei stetigen Verteilungen die Wahrscheinlichkeitsdichte an. Um die Wahrscheinlichkeit, dass der Messwert im Intervall @a, bD liegt, zu berechnen muss die Wahrscheinlichkeitsdichte von a bis b
integriert werden, dies liefert:
b
1 ji ij b - 5 yz
i a - 5 yzzy
Å jerf j ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ zz - erf jjj ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ zzzz
‡ pdfHxL „ x = ÅÅÅÅÅ
è!!!!
2 jk jk è!!!!
a
2 {
k 2 {{
2
Die Funktion erf ist dabei die bekannte Funktion: erf HzL = ÅÅÅÅ
ÅÅÅÅ!ÅÅ Ÿ0 e-t dt
è!!!!
p
z
2
Alternativ könnte man auch die CDF verwenden, die diese Integration definitionsgemäss bereits für das Intervall
D - ¶, xD durchgeführt hat. Die Differenz der CDF an zwei Punkten a und b liefert:
1 i i b - 5 zy
i a - 5 zyzy
cdfHbL - cdfHaL = ÅÅÅÅÅÅ jjjerf jjj ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ ÅÅ zz - erf jjj ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ zzzz
è!!!!
2 k k è!!!!
2 {
k 2 {{
Wir sehen, dass das gleiche Resultat resultiert. Wir können also entweder die PDF über das Intervall integrieren oder
die Differenz der CDF an den beiden Intervallgrenzen bilden.
Wenn wir ein ganz bestimmtes Intervall wählen (z.B. @6, 7D), dann können wir einen Zahlenwert für die Wahrscheinlichkeit erhalten und zwar:
7
‡ pdfHxL „ x = 0.1359
6
32
Skript Statistik und Stochastik
0.4
0.3
0.2
0.1
2
4
6
8
10
Wir schliessen aus obiger Berechnung, dass die Wahrscheinlichkeit bei einer Normalverteilung mit dem Mittelwert 5 und der
Standardabweichung 1 einen Messwert zwischen 6 und 7 zu finden durch die Fläche unter der Kurve gegeben ist und 13.59%
beträgt.
Wir haben auch gesehen, dass wir mit der CDF eine sehr einfache Möglichkeit haben, von Messintervallen (Abszisse:
@a, bD) auf Wahrscheinlichkeiten (Ordinate: cdf @bD - cdf@aD) zu schliessen.
1
0.8
0.6
0.4
0.2
2
4
6
8
10
Wir erhalten für unser Beispiel die folgenden Zahlenwerte:
cdf@7D = 0.97725
cdf@6D = 0.841345
cdf@7D - cdf@6D = 0.135905
bzw. 13.59%
Interpretation (der Graphik und der Zahlen):
† die Wahrscheinlichkeit, einen Messwert kleiner als 7 zu finden ist 97.7%;
† die Wahrscheinlichkeit, einen Messwert kleiner als 6 zu finden ist 84.1%;
† die Wahrscheinlichkeit, einen Messwert im Intervall [6,7] zu finden ist 13.59% (wie oben bei der Integration);
† man sieht auch, dass die Wahrscheinlichkeit, einen Messwert kleiner als 2 zu finden, (praktisch) 0 ist;
† man sieht auch, dass die Wahrscheinlichkeit, einen Messwert kleiner 8 zu finden, (praktisch) 1 ist;
In der Schätztheorie werden wir auch auf die umgekehrte Aufgabe stossen, nämlich von Ordinatenwerten (Wahrscheinlichkeit oder Wahrscheinlichkeitsintervall) auf Abszissenwerte (Messwert oder Messintervall) zu schliessen.
Dazu muss die inverse Funktion zur Verteilung verwendet werden: sie wird mit Quantile (hier für unsere Normalverteilung mit Mittelwert 5 und Standardabweichung 1 quantile genannt) bezeichnet.
[email protected] = 7.
[email protected] = 6.
33
Skript Statistik und Stochastik
Statt Quantile aufzurufen (d.h. [email protected]) können wir aber auch die Gleichung
cdf@xD = 0.97725
(numerisch) nach x auflösen (z.B. mit FindRoot in Mathematica).
Im Rahmen der Schätztheorie werden wir noch ausführlich von diesen Funktionen (PDF, CDF, Quantile) Gebrauch
machen.
Diskrete Verteilung
Zum Schluss wollen dir doch noch einen kleinen Blick auf diskrete Verteilungen werfen.
Wir haben in der Einleitung behauptet, dass die CDF der Summe der Wahrscheinlichkeiten entspricht. Wir vergleichen
deshalb diese beiden Formeln für konkrete Werte:
n = 10; p = 0.5; x = 3;
:‚ PDFHBinomialDistributionHn, pL, iL, CDFHBinomialDistributionHn, pL, xL>
x
i=0
80.171875`, 0.1718750000000001`<
Die beiden Summen sind (im Rahmen der Rechengenauigkeit) identisch.
Erwartungswert
Wenn wir Zufallsexperimente durchführen (oder Daten analysieren), dann interessieren wir uns vielfach für quantitative Aussagen: z.B. wie gross ist die mittlere Augenzahl beim Würfeln oder wie gross ist die Abweichung von diesem
Mittelwert. Der Begriff des Erwartungswerts liefert uns solche Werte. Er ist folgendermassen definiert.
Der Erwartungswert ist die Summe der Produkte aus den Wahrscheinlichkeiten jedes möglichen Ergebnisses des Experiments
und den Werten dieses Ergebnisses.
Wenn die Zufallsvariable X diskret ist und die Werte x1 x2, ... mit den Wahrscheinlichkeiten p1 , p2, ... annehmen kann,
dann ist der Erwartungwert von X , d.h. EHX L, folgendermassen definiert (n kann auch ¶ sein, dann existiert der
Erwartungswert nur, wenn die unendliche Reihe konvergiert):
EHX L = ⁄ni=1 xi pi
Wenn die Zufallsvariable X stetig ist und die Wahrscheinlichkeitsdichtefunktion pHxL hat, dann ist der Erwartungwert
von X , d.h. EHX L, folgendermassen definiert:
EHX L = Ÿ-¶ x pHxL „ x
¶
Heuristisch ist der Erwartungswert einer Zufallsvariablen jener Wert, der sich bei einer oftmaligen Wiederholung des zugrunde
liegenden Experiments als Mittelwert der tatsächlichen Ergebnisse ergibt. Das Gesetz der grossen Zahlen sichert uns in den
meisten Fällen zu, dass dieser heuristische Wert mit der mathematischen Definition übereinstimmt.
Wenn Y = gHX L auch eine Zufallsvariable ist, kann der Erwartungswert dieser Zufallsvariablen folgendermassen
berechnet werden:
EHY L = Ÿ-¶ gHxL pHxL „ x
¶
bzw.
EHY L = ⁄ni=1 gHxi L pi
Skript Statistik und Stochastik
34
Beispiel Würfeln
Als Beispiel für einen Erwartungswert wollen wir das Zufallsexperiment Würfeln und als (diskrete) Zufallsvariable X
die "Augenzahl" wählen. Wir haben die möglichen Ergebnisse 81, 2, 3, 4, 5, 6< mit den (gleichen) Wahrscheinlichkeiten 1/6. Der Erwartungswert für die Augenzahl berechnet sich damit zu 3.5:
6
i
7
‚ ÅÅÅÅÅÅ = ÅÅÅÅÅÅ
6
2
i=1
Dieser Wert wird sich bei einer grossen Anzahl von Wiederholungen (approximativ, jedoch nicht genau) einstellen.
Wenn wir z.B. 5 Versuche mit je 106 x würfeln durchführen, erreichen wir (in einem Computerexperiment) beispielsweise die folgenden Durchschnitte:
83.4987451`, 3.5000078`, 3.5002974`, 3.500247`, 3.4999695`<
Diese Durchschnitte liegen nahe beim Erwartungswert. Bei nur 10 Wiederholungen (statt 106 ) kann die Abweichung
von 3.5 gross sein.
83.5`, 4.1`, 4.2`, 3.6`, 3.8`<
Diskrete Verteilungen
Einleitung
Es gibt viele verschiedene Diskrete Verteilungen. Mathematica hat die folgenden acht implementiert:
BernoulliDistribution, BinomialDistribution, DiscreteUniformDistribution, GeometricDistribution, HypergeometricDistribution, LogSeriesDistribution, NegativeBinomialDistribution, PoissonDistribution}.
Nicht alle sind gleich wichtig. Wir werden uns vor allem mit der Gleichverteilung, der Bernoulli Verteilung, der
Poisson Verteilung und der Binomial Verteilung beschäftigen. Diese Verteilungen folgen direkt aus verschiedenen
experimentellen Situationen.
† Die Gleichverteilung resultiert beim Würfeln oder beim Ziehen einer Kugel aus einer Urne.
Die Bernoulli Verteilung, die Poisson Verteilung, die Binomial Verteilung sowie weitere Verteilungen resultieren bei
der Durchführung einer Bernoulli Versuchsreihe, wo bei jeder Wiederholung die gleiche Ausgangssituation vorliegt
(z.B. Ziehen mit Zurücklegen).
Das Bernoulli Experiment hat die zwei möglichen Ergebnisse 81 = Erfolg, 0 = Misserfolg< und der Erfolg tritt mit der
Wahrscheinlichkeit p und der Misserfolg mit der Wahrscheinlichkeit 1 - p auf. Es folgt nun.
† Die Wahrscheinlichkeitsfunktion der Bernoulli Verteilung B@1, pD @kD gibt beim 1-maligen Versuch die Wahrscheinlichkeiten für k (d.h. 0 oder 1) Erfolge an.
† Die Wahrscheinlichkeitsfunktion der Binomial Verteilung B@n, pD @kD gibt beim n-maligen Duchführen eines
iny
Bernoulli Experiments die Wahrscheinlichkeit für k Erfolge an und hat die Formel H1 - pLn-k pk jj zz
kk {
† Die Wahrscheinlichkeitsfunktion der Poisson Verteilung P@l = n pD @kD gibt beim n-maligen Duchführen eines
‰-l lk
Bernoulli Experiments die Wahrscheinlichkeit für k Erfolge an und hat die Formel ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ . Sie wird bei grossen n
k!
und kleinen p angewendet und stellt eine Approximation für die Binomial Verteilung B@n, pD @kD dar.
35
Skript Statistik und Stochastik
† Die Wahrscheinlichkeitsfunktion der NegativeBinomialDistribution gibt die Wahrscheinlichkeit für k Misserfolge
i k + r - 1 zy
vor dem r-ten Erfolg an und hat die Formel f @ p, rD @kD = jj
z H1 - pLk pr .
k r-1 {
† Die Wahrscheinlichkeitsfunktion der GeometricDistribution gibt die Wahrscheinlichkeit für k Misserfolge vor dem
ersten Erfolg an und hat die Formel f @ pD @kD = H1 - pLk p.
Beim Experiment "Ziehen mit Zurücklegen" handelt es sich nicht um eine Bernoulli Versuchsreihe, da sich die Wahrscheinlichkeiten für Erfolg und Misserfolg im Laufe der Versuchsreihe ändern.
So ändert sich z.B. bei einem Experiment, wo sich in einer Urne mit N Kugeln M rote und N - M weisse Kugeln
befinden, die Wahrscheinlichkeit (eine rote Kugel zu ziehen) mit jedem Zug. Eine genaue Analyse dieser Situation
führt uns auf die Hypergeometrische Verteilung. Es gilt:
† Die Wahrscheinlichkeitsfunktion der Hypergeometrische Verteilung H@N, M , n, mD gibt (für obige Situation) beim
n-maligen Ziehen die Wahrscheinlichkeit für m rote Kugeln an. Diese Verteilung hat die Formel pHkL =
M
Diese Verteilung konvergiert für grosse N gegegen die Binomialverteilung B@n, pD mit p = ÅÅÅÅ
ÅÅ .
N
M N-M y
jij zyz jij
zz
k m { k n-m {
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
Å
Å
Å
ij N yz
j z
n
k {
.
Es gibt weitere Verteilungen, die anwendbar sind auf Experimente mit mehr als zwei Ergebnissen (z.B. Trinomial
Verteilung und Bivariate Hypergeometrische Verteilung bei drei Ergebnissen). Wir werden diese jedoch hier nicht
weiter besprechen.
In den folgenden Abschnitten werden wir einige diskrete Verteilungen etwas genauer anschauen.
Gleichverteilung (DiscreteUniformDistribution)
Einleitung
Die gleichförmige Verteilung(Gleichverteilung) basiert auf dem Gleichwahrscheinlichkeitsmodell. Die Zufallsvariable X hat n
Ausprägungen, wobei alle Ausprägungen mit gleicher Wahrscheinlichkeit vorkommen. Diese Wahrscheinlichkeit muss 1 ê n
betragen, da die gesamte Wahrscheinlichkeit stets 1 sein muss.
Die Wahrscheinlichkeitsfunktion der Gleichverteilung ist (für n = 5) auf dem Träger 81, 2, 3, 4, 5< ungleich 0 und hat
den konstanten Wert ÅÅÅÅ15 .
Der Plot der Wahrscheinlichkeiten sieht damit folgendermassen aus.
0.2
0.15
0.1
0.05
2
4
6
Die CDF liefert uns die kumulierte Wahrscheinlichkeit. Sie steigt in gleichen Schritten für die Abszissenwerte 1 bis 5.
36
Skript Statistik und Stochastik
1
0.8
0.6
0.4
0.2
2
4
6
8
Beispiele für Gleichmässige Verteilung:
† Die Zufallsvariable, die definiert ist durch die Nummer der Kugel beim einmaligen, zufälligen Ziehen aus einer
Urne mit n Kugeln; oder
† Die Zufallsvariable "Augenzahl" beim Würfeln (n=6);
Eigenschaften
Die gleichförmige Verteilung hat die folgenden wichtigen Eigenschaften.
DiscreteUniformDistribution@nD
Domain:
PDF:
CDF:
Mean:
Variance:
Range@nD
1
n
Floor@xD
n
1+n
2
1
H−1 + n2 L
12
Die Funktion Floor@xD = dxt bedeutet dabei die grösste ganze Zahl, die § x ist.
Die Funktion Range@xD bedeutet dabei die Zahlenfolge 81, 2, ... x<.
Beispiel
Der arithmetische Mittelwert beim Würfeln (n=6) beträgt
1
35
ÅÅ H-1 + 62 L = ÅÅÅÅ
ÅÅ
s = ÅÅÅÅ
12
12
1+n
1+6
ÅÅÅÅÅÅ = ÅÅÅÅ
m = ÅÅÅÅ
ÅÅÅÅÅÅ = ÅÅÅÅ72
2
2
und hat die Varianz
Bernoulli Verteilung (BernoulliDistribution)
Einleitung
Beim Bernoulli Experiment hat die Zufallsvariable nur die beiden möglichen Ausprägungen 0 und 1, wobei 0 üblicherweise
als Misserfolg und 1 als Erfolg bezeichnet wird. Der Erfolg (1) tritt dabei mit einer Wahrscheinlichkeit p auf. Das
komplementäre Ereignis Misserfolg hat demnach die Wahrscheinlich 1 - p.
Die Wahrscheinlichkeitsfunktion der Bernoulli-Verteilung ist auf dem Träger 80, 1< ungleich 0 und hat (für p = 0.75)
folgende Werte:
µ
0.25
0.75
x0
x1
Ein Plot der Wahrscheinlichkeitsverteilung zeigt dies anschaulich:
37
Skript Statistik und Stochastik
1
0.8
0.6
0.4
0.2
-1
-0.5
0.5
1
1.5
2
Die CDF erreicht bereits bei x = 1 das Maximum von 1.
1
0.8
0.6
0.4
0.2
-1
-0.5
0.5
1
1.5
2
Man kann aus diesem Plot (z.B.) herauslesen, dass die Wahrscheinlichkeit einen Wert §1 zu finden gleich 1 ist.
Beispiel:
Bernoulli(0.5) entspricht einem Münzwurf.
Eigenschaften
Die Bernoulli Verteilung hat die folgenden wichtigen Eigenschaften.
BernoulliDistribution@pD
Domain:
PDF:
CDF:
Mean:
Variance:
80, 1<
1−p x 0
µ
p
x1
1−p 0≤x<1
µ
1
x≥1
p
H1 − pL p
Beispiel
Der arithmetische Mittelwert beim Münzen werfen ( p = 0.5, Kopf = 0, Zahl = 1) beträgt 0.5 und hat die Varianz
0.25.
38
Skript Statistik und Stochastik
Binomial Verteilung (BinomialDistribution bzw. BINOMVERT)
Einleitung
Mehrere (n) Bernoulli Experimente mit derselben Erfolgswahrscheinlichkeit p werden unabhängig voneinander
durchgeführt (z.B. n mal Münzen werfen oder n Kugeln mit Zurücklegen aus einem Topf mit Kugeln aus zwei verschiedenen Farben ziehen).
Die Anzahl der Erfolge wird als Zufallsvariable Sn definiert. Die Wahrscheinlichkeit, dabei genau k Erfolge zu messen, führt
auf die Binomial Verteilung, die vielfach kurz als BHn, pL bezeichnet wird. Eine Verteilung mit dieser
Wahrscheinlichkeitsfunktion (mit 0 § p § 1, n œ ) heisst binomialverteilt.
Die Wahrscheinlichkeitsfunktion der Binomial-Verteilung ist auf dem Träger 80, 1, ... n< ungleich 0 und hat den
iny
folgenden Wert H1 - pLn-k pk jj zz.
kk{
Ein Plot der Wahrscheinlichkeitsfunktion (n = 20, p = 0.5, z.B. 20 mal Münze werfen) zeigt (gegen k aufgetragen)
anschaulich die Symmetrie:
0.175
0.15
0.125
0.1
0.075
0.05
0.025
5
10
15
20
Man kann ausrechnen, dass die Wahrscheinlichkeit beim Münzenwerfen 20 mal Kopf zu werfen klein ist (9.5 µ 10-7 ),
jedoch nicht gleich 0.
Die CDF steigt kontinuierlich an bis auf den Wert 1 bei x = 20.
1
0.8
0.6
0.4
0.2
5
10
15
20
1
Bemerkungen
† Man sieht, dass die Binomialverteilung zwei Parameter Hn, pL hat. Sie bildet eine sogenannte Zwei-Parameter-Familie.
† Wenn man n = 1 setzt, erhält man die Bernoulli Verteilung.
39
Skript Statistik und Stochastik
† Alle Binomialverteilungen mit p = 0.5 sind symmetrisch. Für p  0.5 erhält man linkssteile, sonst rechtssteile
Verteilungen.
† Die Binomialverteilung BHn, pL nähert sich für grosse n der Normalverteilung mit Mittelwert n p und Varianz
n pH1 - pL, also NHn p, n pH1 - pLL.
Eigenschaften
Die Verteilung hat die folgenden wichtigen Eigenschaften.
BinomialDistribution@n, pD
Domain:
PDF:
CDF:
Mean:
Variance:
Range@0, nD
H1 − pLn−x px Binomial@n, xD
BetaRegularized@1 − p, n − Floor@xD, 1 + Floor@xDD
np
n H1 − pL p
Die Funktion Range@0, xD bedeutet dabei die Zahlenfolge 80, 1, 2, ... x<.
Siehe die mathematische Fachliteratur für Informationen zur CDF Funktion BetaRegularized.
Die Anzahl der Erfolge beim n-maligen Münzen werfen.
Die PDF ergibt folgenden Plot ( p = 0.5, n = 20).
0.175
0.15
0.125
0.1
0.075
0.05
0.025
5
10
15
20
Man kann dem Plot (z.B.) entnehmen, dass bei 20 Münzenwürfen die Wahrscheinlichkeit rund 7.5% beträgt, 13 mal
Zahl zu werfen. Den genauen Wert liefert PDFHBinomialDistributionH20, 0.5L, 13L = 0.0739288
Beispiel 1
Bestimmen Sie die Wahrscheinlichkeiten, bei 20 Zügen k rote Kugeln zu ziehen, wenn sich in der Urne 2 rote und 8 blaue
Kugeln befinden.
2
Die Wahrscheinlichkeit ist gegeben durch die Binomialverteilung BH20, ÅÅÅÅ
ÅÅ L. Dies gibt den folgenden Plot:
10
40
Skript Statistik und Stochastik
0.2
0.15
0.1
0.05
5
Beispielrechnung für k = 15:
Beispielrechnung für k = 5:
10
15
20
iny
i 20 y
H1 - pLn-k pk jj zz = 0.85 0.215 jj zz = 1.66473 µ 10-7
kk {
k 15 {
iny
i 20 y
H1 - pLn-k pk jj zz = 0.815 0.25 jj zz = 0.17456
kk {
k 5 {
Beispiel 2
Sie würfeln 10x. Bestimmen Sie die Wahrscheinlichkeiten, k-mal mindestens eine 5 zu würfeln.
2
Bei jedem Wurf ist die Wahrscheinlichkeit, eine Augenzahl von mindestens 5 zu werfen 6 .
Bei 10 Würfen ist die Erfolgswahrscheinlichkeit, k mal (k = 0, ... 5) eine 5 zu werfen, durch die Binomialverteilung
BH10, ÅÅ26ÅÅ L gegeben. Dies gibt den folgenden Plot:
0.25
0.2
0.15
0.1
0.05
2
4
6
8
10
Beispiel 3
Sie würfeln 5x. Mit welcher Wahrscheinlichkeit resultiert zweimal eine 6?
1
Bei jedem Wurf ist die Wahrscheinlichkeit, eine 6 zu werfen 6 .
Bei 5 Würfen ist die Erfolgswahrscheinlichkeit, 2 mal eine 6 zu werfen, durch die Binomialverteilung gegeben:
5-2
2i5y
iny
H1 - pLn-k pk jj zz = H1 - ÅÅÅÅ16 L H ÅÅÅÅ16 L jj zz = 0.160751
kk {
k2{
41
Skript Statistik und Stochastik
Poisson Verteilung (PoissonDistribution bzw. POISSON)
Einleitung
Die Verteilung p heisst Poisson Verteilung mit Parameter l mit l œ (0,¶), wenn gilt:
‰-l lk
ÅÅÅÅÅÅÅÅ
pHl, kL ÅÅÅÅÅÅÅÅ
k!
Sie approximiert die Binomialverteilung BHn, kL und findet Anwendung für grosse Werte von n und sehr kleine Werte von p
(mit l = n p ). Die Poisson Verteilung hat den Mittelwert l und die Varianz l.
Die Wahrscheinlichkeitsfunktion der Poisson Verteilung ist auf dem Träger k œ 80, 1, 2. .. ¶< ungleich 0 und hat den
‰-l lk
ÅÅÅÅÅÅ .
folgenden Wert ÅÅÅÅÅÅÅÅ
k!
Sie hat beispielsweise (für l = 10) für k = 6 den folgenden Wert: 0.0630555
Ein Plot zeigt die Wahrscheinlichkeitsverteilung anschaulich (für l = 10):
0.12
0.1
0.08
0.06
0.04
0.02
5
10
15
20
25
30
Eigenschaften
Die Verteilung hat die folgenden wichtigen Eigenschaften.
PoissonDistribution@λD
Domain:
PDF:
CDF:
Mean:
Variance:
Range@0, ∞D
−λ λx
x!
GammaRegularized@1 + Floor@xD, λD
λ
λ
Siehe die mathematische Fachliteratur für Informationen zur CDF Funktion GammaRegularized.
Stetige Verteilungen
Einleitung
Es gibt viele Stetige Verteilungen. Mathematica hat beispielsweise die folgenden einundzwanzig implementiert:
ChiSquareDistribution, FRatioDistribution, NormalDistribution, StudentTDistribution, BetaDistribution,
CauchyDistribution, ChiDistribution, ExponentialDistribution, ExtremeValueDistribution, GammaDistribution,
HalfNormalDistribution, LaplaceDistribution, LogisticDistribution, LogNormalDistribution, NoncentralChi-
42
Skript Statistik und Stochastik
SquareDistribution, NoncentralFRatioDistribution, NoncentralStudentTDistribution,
RayleighDistribution, UniformDistribution, WeibullDistribution.
ParetoDistribution,
Wir werden uns in dieser Vorlesung vor allem mit der NormalDistribution, der UniformDistribution, der ChiSquareDistribution sowie der StudentTDistribution beschäftigen.
Normalverteilung (NormalDistribution bzw. NORMVERT, STANDNORMVERT)
Einleitung
Die Normalverteilung ist die wichtigste stetige Verteilung und zwar aus folgenden Gründen:
† Gemäss zentralem Grenzwertsatz (siehe später) haben Summen von Zufallsgrössen approximativ eine Normalverteilung. Dies erklärt, dass viele Phänomende der Natur, welche sich aus vielen Einzelereignissen zusammensetzen,
eine Normalverteilung haben.
† Die Normalverteilung maximiert die Entropie. Damit maximiert man die Unwissenheit. Damit drängt sich die
Normalverteilung zur Modellierung von Fehlern auf, wenn man keine weiteren Anhaltspunkte hat.
† Viele Prozesse mit exponentiellem Wachstum (Modelle von Aktienkursen oder ganzen Volkswirtschaften) sind
Lognormalverteilt (d.h. nach Logarithmierung normalverteilt).
† Die Normalverteilung hat schöne mathematische Eigenschaften. Sie ist symmetrisch und die Wahrscheinlichkeitsdichte geht sehr schnell gegen 0.
Die Normal-Verteilung ist eine zwei Parameter Familie von Verteilungen. Der erste Parameter ist der Mittelwert der
Verteilung, der zweite Parameter ist die Standardabweichung (bzw. Varianz) der Verteilung. Sie wird vielfach kurz als
NHm, s2 L bezeichnet.
Die Wahrscheinlichkeitsfunktion der Normalverteilung ist auf dem Träger @-¶, ¶D ungleich 0 und hat den folgenden
2
H−m+xL
− 2
2s
Wert mit Mittelwert m und Standardabweichung s.
è!!!!!!!!
2π s
Sie hat folgendes (symmetrisches) Aussehen (mit m = 5 und s = 1):
0.4
0.3
0.2
0.1
2
4
6
8
10
Die Wahrscheinlichkeitsdichte der Normalverteilung (PDF) sowie die im folgenden abgebildete CDF spielen eine
zentrale Rolle in der induktiven Statistik sowie der Schätz- und Testtheorie. Wir werden später darauf zurückkommen.
43
Skript Statistik und Stochastik
1
0.8
0.6
0.4
0.2
2
4
6
8
10
Eigenschaften
Die Verteilung hat die folgenden wichtigen Eigenschaften.
NormalDistribution@m, sD
Domain:
Interval@8−∞, ∞<D
PDF:
2 s2
− è!!!!!!!!
2π s
H−m+xL2
CDF:
Mean:
Variance:
1 i
−m + x y
z
j
j1 + ErfA è!!!! Ez
2 k
2 s {
m
s2
Standardnormalverteilung
Eine Normalverteilung mit Mittelwert 0 und Standardabweichung 1 wird Standardnormalverteilung genannt.
Sie wird oft auch mit N@0, 1D bezeichnet.
Die PDF und CDF der Standardnormalverteilung sind tabelliert. Aus diesen Tabellen lassen sich die Wahrscheinlichkeiten für normierte Messwertintervalle herauslesen.
Wir können einfacher und schneller (statt der Tabellen) die CDF verwenden. Wichtig zu wissen ist, dass die folgenden
Beziehungen gelten (mit m = Mittelwert und s = Standardabweichung):
0.5`
1.`
2.`
3.`
4.`
0.382925
0.682689
0.954500
0.997300
0.999937
38.2925 % der Beobachtungen liegen im Intervall @m - 0.5 s, m + 0.5 sD
68.2689 % der Beobachtungen liegen im Intervall @m - 1 s, m + 1 sD
95.4500 % der Beobachtungen liegen im Intervall @m - 2 s, m + 2 sD
99.7300 % der Beobachtungen liegen im Intervall @m - 3 s, m + 3 sD
99.9937 % der Beobachtungen liegen im Intervall @m - 4 s, m + 4 sD
Man sieht, dass die Wahrscheinlichkeit, einen Wert ausserhalb von @-4 s, 4 sD zu messen, weniger als 0.01 % beträgt,
also äusserst unwahrscheinlich ist.
44
Skript Statistik und Stochastik
c2 Verteilung (ChiSquareDistribution bzw. CHIVERT)
Einleitung
Diese Verteilung ist in der Statistik sehr wichtig und verdankt ihre Existenz weitgehend dem zentralen Grenzwertsatz
und der Tatsache, dass man in Modellen der Datenanalyse Fehlerterme normalverteilt modelliert. Dann haben folgende
Zufallsvariablen eine cn 2 Verteilung.
† ⁄ni=1 Xi 2 , falls die Xi (i = 1, .. n) standardnormalverteilt sind;
êêê 2
n
n
êêê
HYi -Y L
Yi
† ‚ ÅÅÅÅÅÅÅÅ
ÅÅÅÅ2 ÅÅÅÅÅÅ , falls die Yi (i = 1, .. n) normalverteilt sind mit Mittelwert Y = ‚ ÅÅÅÅ
Å und Varianz s2 ;
s
i=1
i=1 n
n
êêê 2
S2
† Ausserdem hat ÅÅÅÅ
ÅÅÅ eine cn-1 2 Verteilung, wobei S 2 = ‚ HYi - Y L ;
s2
i=1
Wir werden später noch genauer darauf zurückkommen.
Die Wahrscheinlichkeitsfunktion der c2 Verteilung ist auf dem Träger @0, ¶@ ungleich 0 und hat den folgenden Wert
-nê2
-xê2
n
-1+ ÅÅ2ÅÅÅ
2
‰
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅxÅÅÅÅÅÅÅÅÅÅÅÅÅ . Sie ist also für negative x nicht definiert.
Gamma@ ÅÅÅÅn D
2
Der folgende Plot zeigt die Verteilung für verschiedene n: 81, 2, 3, 5, 10, 20< in den Farben {rot, grün, blau, rot-strichliert, grün-strichliert, blau-strichliert}.
Der folgende Map Befehl erzeugt eine Liste von Graphiken, die als Animation betrachtet werden können. Auf diese
Art und Weise sieht man sehr schön, wie sich die ChiSquareDistribution mit zunehmendem Parameter (Anzahl
Freiheitsgrade) verändert.
0.3
0.25
0.2
0.15
0.1
0.05
5
10
15
20
25
Eigenschaften
Die Verteilung hat die folgenden wichtigen Eigenschaften.
ChiSquareDistribution@nD
Domain:
Interval@80, ∞<D
PDF:
2−nê2 −xê2 x−1+ 2
n Gamma@ D
2
n
CDF:
Mean:
Variance:
n
x
GammaRegularizedA , 0, E
2
2
n
2n
Student t Verteilung (StudentTDistribution bzw. TVERT)
Die Wichtigkeit der StudentTDistribution leitet sich von folgender Eigenschaft ab.
45
Skript Statistik und Stochastik
Y
Falls Y eine standardnormalverteilte Zufallsgrösse und Z eine cn 2 verteilte Zufallsgrösse ist, dann ist der Quotient Tn = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ
"#######
Z
ÅÅnÅÅ
StudentT verteilt.
Die Wahrscheinlichkeitsfunktion der Student t Verteilung ist auf dem Träger D - ¶, ¶@ ungleich 0 und hat den foln
I ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ M 2
n+x2
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ .
è!!!!! ÅÅÅÅÅÅÅÅ
n Beta@ ÅÅÅÅn2 , ÅÅÅÅ12 D
1+n
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
genden Wert
Die folgende Graphik zeigt sehr schön, dass mit zunehmendem n (Anzahl Freiheitsgrade): {1 rot, 2 grün,3 blau,5 rot
strichliert,10 grün strichliert,100 blau strichliert}die StudentTDistribution gegen die Standardnormalverteilung konvergiert. In der Praxis ist es üblich, für einen Parameter grösser als 100 die StudentTDistribution durch die Standardnormalverteilung zu ersetzen. Wie man sieht, ist dies gerechtfertigt.
0.4
0.3
0.2
0.1
-4
-2
2
4
Eigenschaften
Die Verteilung hat die folgenden wichtigen Eigenschaften.
StudentTDistribution@nD
Domain:
Interval@8−∞, ∞<D
PDF:
n
H L 2
n+x2
è!!!!
n
1
n Beta@ , D
2
2
1+n
CDF:
Mean:
Variance:
1
n
n
1
J1 + BetaRegularizedA , 1, , E Sign@xDN
2
n + x2
2
2
0
n
−2 + n
46
Skript Statistik und Stochastik
Zentraler Grenzwertsatz
Einleitung
Der Graph der Verteilungsfunktion einer Summe von n unabhängigen, identisch verteilten Zufallsvariablen mit endlicher
Varianz gleicht für grosse n mehr und mehr einer Normalverteilung.
Diese bemerkenswerte Tatsache ist eines der fundamentalen Ergebnisse der Wahrscheinlichkeitstheorie und wird der
"Zentrale Grenzwertsatz" genannt.
1
Wir werden diesen Satz nicht beweisen. Wir wollen dies jedoch mit der Bernoulli( 2 ) Verteilung illustrieren. Diese
1
.
Bernoulli Verteilung hat die Werte 0 und 1 mit der Wahrscheinlichkeit von je 2
Experiment
Der zentrale Grenzwertsatz bezieht sich auf eine Summe von Zufallsvariablen, also auf die Summe der Ergebnisse von
n-mal durchgeführten Bernoulli Experimenten. Es interessiert nun nicht diese Summe, sondern die Verteilung dieser
Summe (aus n Experimenten), wenn n gegen ¶ geht.
Ein Wurf ergibt die zwei möglichen Pfade bzw. Summe {0} und {1} mit je 50% Wahrscheinlichkeit:
Zwei Würfe ergeben bei 4 verschiedenen Pfaden die Summen {0}, {2} mit je 25% Wahrscheinlichkeit und {1} mit
50% Wahrscheinlichkeit.
Fünf Würfe ergeben den folgenden Plot der 8Summe, Anzahl Pfade<-Paare.
10
8
6
4
2
5
10
15
20
Die Verteilung ist weit von einer Normalverteilung entfernt. Wenn wir jedoch die Anzahl Münzwürfe weiter erhöhen,
wird die Verteilung immer symmetrischer und ähnlicher zu einer Normalverteilung. Bei 20 Würfen gibt es total
220 = 1048576 verschiedene Pfade (Variationen). Rund 175'000 dieser Pfade ergeben dabei als Summe 10 (bzw. 10x
das Einzelergebnis {1}).
47
Skript Statistik und Stochastik
175000
150000
125000
100000
75000
50000
25000
5
10
15
20
Die PDF selbst konvergiert jedoch nicht für grosse n gegen eine bestimmte Kurve. Der Erwartungswert sowie die
Varianz nehmen nämlich kontinuierlich zu (gegen ¶). Dies ist auch zu erwarten, da der Erwartungswert der Bernoullivn
n
erteilung bei n Versuchen 2 beträgt und die Varianz 4 .
Man kann jedoch diese PDF so normieren, dass sie den Erwartungswert 0 und die Varianz 1 hat. Diese PDF konvergiert dann gegen die Standard Normalverteilung.
Obwohl die Ausgangswahrscheinlichkeitsfunktion mit den beiden Ergebnissen {0} und {1} weit von einer Normalverteilung
entfernt ist, konvergiert die Summe für grosse n gegen die Normalverteilung.
Kugeln aus einer Urne ziehen
Hier wird nun eine weitere Illustration des zentralen Grenzwertsatzes gegeben.
Gegeben ist eine Box, in der sich Kugeln mit den Nummern 0, 2, 3, 4 und 6 befinden. Dies ist wiederum eine Ausgangswahrscheinlichkeitsfunktion, die weit von einer Normalverteilung entfernt ist.
Es werden nun 25 Kugeln mit Zurücklegen gezogen und die Nummern addiert. Dies gibt eine Zahl im Bereich von 0 (
25 mal die 0) bis 150 (25 mal die 6).
Wenn wir nun 5x je 25 Kugeln ziehen, resultieren (in einem Computerexperiment) die folgenden Summen:
8102, 84, 70, 88, 80<
Dieses Experiment wird nun nicht 5 mal, sondern 100 mal ...
6
5
4
3
2
1
20 40 60 80 100120140
... bzw. 10'000 mal repetiert.
400
300
200
100
20
40
60
80 100 120 140
Skript Statistik und Stochastik
48
Man sieht, dass mit der Anzahl der Wiederholungen die Verteilung gleichmässiger wird.
Im obigen Prozedere muss man zwischen der Anzahl Züge (25) und der Anzahl Wiederholungen (10'000) unterscheiden.
Wenn die Anzahl Züge zunimmt (z.B. 50 statt 25), wird sich das diskrete (theoretische) Wahrscheinlichkeitshistogramm für die Summe immer mehr der Normalverteilung annähern. Der Erwartungswert der Summe wird immer
grösser werden und die (relativen) Abstände zwischen den Summen werden immer kleiner (quasistetig).
Wenn die Anzahl der Repetitionen zunimmt, wird sich das empirische Histogramm für die Summe der Züge immer
mehr dem theoretischen Histogramm annähern.
Was auch immer in der Box ist, mit einer genügend grossen Anzahl an Zügen wird das Wahrscheinlichkeitshistogramm (nach
Normierung) immer mehr der Standardnormalverteilung folgen.
Skript Statistik und Stochastik
49
7. Statistik und empirische Daten
Einleitung
Nachdem wir uns bislang vor allem mit der Wahrscheinlichkeitstheorie, mit Zufallsexperimenten und daraus folgenden
(theoretischen) Verteilungen beschäftigt haben, wollen wir uns nun dem Gebiet der Statistik zuwenden, wo es darum
geht (empirische) Daten zu erheben und zu analysieren.
Stichwortartig soll im Folgenden das Gebiet der Statistik umrissen werden.
† Die Statistik ist die Wissenschaft von der Gewinnung, Aufbereitung und Auswertung von Informationen / Daten.
† Die Statistik kann eingeteilt werden in spezielle (auf ein Thema bezogen: z.B. Bevölkerungsstatistik) und allgemeine Statistik.
† Die allgemeine Statistik kann eingeteilt werden in praktische (Erhebung der Daten) und theoretische Statistik.
† Die theoretische Statistik kann eingeteilt werden in beschreibende (deskriptive) und schliessende (induktive,
inferentielle) Statistik.
† Bei der deskriptiven Statistik geht es darum, die Daten zu beschreiben. Dies geschieht mittels Masszahlen und
Graphiken. Stichworte:
† Positionsmass bzw. Lokalisationsmass: Mean, Median, Min, Max, Quantile
† Streuungsmass bzw. Dispersionsmass: Standardabweichung, Varianz, Spanne, Skewness (Schiefe), Kurtosis
(Wölbung), KurtosisExcess (Exzess)
† Häufigkeitsauszählung, Kontingenztafel (Kreuztabelle)
† Kovarianz, Korrelation
† Graphiken: Die Darstellung kann von der Urliste, der sortierten Liste (rel. Häufigkeit, Stabdiagramm, Polygonzug) oder gruppierten Daten (Klassen, Balkendiagramm) ausgehen. Es können auch bearbeitete (gefilterte)
Daten dargestellt werden oder mit einem Modell verglichen werden. Weiters gibt es PieChart, BarChart und
BarChart3D (diskret) bzw. Histogram (stetig), BoxAndWhiskerPlot, ListPlot, Plot ...
† Bei der inferentiellen Statistik geht es darum, aus einer Stichprobe (repräsentative Auswahl, Messreihe,
empirische Verteilung) auf eine ganze Population (Grundgesamtheit, theoretische Verteilung) zu schliessen. Sie
kann weiter in Schätztheorie (z.B. Schätzen der theoretischen Verteilung) und Testtheorie unterteilt werden.
Stichworte dazu:
† PDF (probability density function, Wahrscheinlichkeitsdichtefunktion)
† CDF (cumulative density function, Verteilungsfunktion)
† Statistische Test dienen dem Testen von Vermutungen (sogenannten Hypothesen) über Eigenschaften der
Gesamtheit aller Daten (Grundgesamtheit oder Population), aus denen man eine Stichprobe entnommen hat.
Man unterscheidet:
† Hypothesen über die unbekannten Parameter eines bekannten Verteilungstyps. Die zugehörigen Tests
nennt man parametrische Tests.
† Hypothesen über das Symmetriezentrum der Verteilung bei unbekanntem Verteilungstyp
(nichtparametrische Tests).
† Hypothesen über die Art einer Verteilung (Anpassungstests).
† Hypothesen über die Abhängigkeit von Zufallsvariablen (Unabhängigkeitstests).
Skript Statistik und Stochastik
50
† Die Statistik beschäftigt sich mit Daten. Die Daten können verschieden eingeteilt werden
† Einteilung gemäss: quantitativ bzw. metrisch (Real und Integer) versus qualitativ bzw. kategoriell bzw.
nichtmetrisch (diese können weiters in nominal (ohne Rangfolge: z.B. blau, grün, rot) und ordinal (mit
Rangfolge: z.B. schlecht, mittelmässig, gut) unterteilt werden).
† Einteilung gemäss: kontinuierlich bzw. stetig (Real) versus diskret (Integer, Kategorien)
† Die Daten liegen als Listen (univariate Daten) oder Tabellen mit zwei (bivariat) oder mehr (multivariate)
Spalten vor.
† In einer Reihe (Zeile) stehen die Werte (aller Variablen) für eine Messung / Beobachtung.
† In einer Kolonne (Spalte) stehen die Werte (aller Messungen) für ein bestimmtes Merkmal (Variable).
† Schritte bei der Analyse von Daten
† Deskriptive Statistik: Positionsmasse, Dispersionsmasse, ... Graphiken
† Korrelationen (bei multivariaten Daten)
† Filtern und Vorverarbeiten von Daten: ZeroMean, Standardize
† Test auf Normalverteilung (oder eine andere Verteilung)
† Schliessen von der Stichprobe auf die Population
Datentypen
Wir wollen hier noch etwas detaillierter (als im vorherigen Abschnitt) auf die verschiedenen Datentypen (bzw. Merkmalstypen) eingehen.
Es lassen sich drei Merkmalstypen unterscheiden
† Klassifikatorische (qualitative) Merkmale; abzählbar viele Ausprägungen; die möglichen Merkmalsausprägungen
werden auf einer Nominalskala erfasst, bei der die Skalenwerte lediglich als Kennzahlen (Namen für die Objekte)
aufgefasst werden können: Geschlecht, Haarfarbe.
† Komparative Merkmale, deren mögliche Ausprägungen intensitätsmässig abgestuft sind und die sich nach einem
Ordnungsprinzip in eine Rangfolge bringen lassen. Die Darstellung derartiger Merkmale erfolgt auf einer Ordinalskala, auf der monotone (oder ordnungserhaltende) Transformationen erlaubt sind: Handelsklassen, Windstärke,
Schulnote.
† Quantitative Merkmale, deren Merkmalsausprägungen digital (Zählvorgang) oder im Vergleich mit einer vorgegebenen Masseinheit analog gemessen werden (Kardinal- oder metrische Skala): Alter, Einkommen, Umsatz.
Bei den quantitativen Merkmalen unterscheidet man drei Skalen:
† Intervallskala, bestimmt dadurch, dass Rangfolge und Abstand zwischen den Merkmalswerten definiert sind;
diese Skala ist gegenüber linearen Transformationen invariant: Temperatur in Grad Celsius.
† Verhältnisskala, bestimmt dadurch, dass Rangfolge, Abstand und Verhältniswert zweier Merkmalswerte
definiert sind; invariant gegenüber ähnlichen Transformationen (y = a x). Es existiert ein natürlicher
Nullpunkt: Körpergrösse.
† Absolute Skala, bestimmt dadurch, dass zusätzlich zu den eine Verhältnisskala definierenden Relationen eine
natürliche Einheit gegeben ist und nur identische Transformationen (y = x) erlaubt sind: Anzahl der Einwohner einer Gemeinde.
Eine weitere Unterscheidung der Merkmale wird durch die jeweilige Angabe der Merkmalswerte getroffen. Diskrete
Merkmale sind Merkmale, deren Wertebereich endlich oder abzählbar unendlich viele Merkmalswerte aufweist.
Kontinuierliche oder stetige Merkmale haben einen Wertebereich mit überabzählbar vielen Merkmalswerten.
Skript Statistik und Stochastik
51
8. Beschreibende Statistik
Einleitung
In der Statistik hat man es häufig mit grossen Datenreihen zu tun. Die als deskriptive Statistik bezeichnete Zweig der
Statistik liefert leistungsstarke Werkzeuge, um solche Datenreihen zu analysieren und Schlüsse daraus zu ziehen.
In diesem Kapitel untersuchen wir Methoden zur Untersuchung eines einzelnen Merkmals X in einer Grundgesamtheit
G = 8e1 , e2 , ... en <. Die Daten sind als Datenvektor x = 8x1 , x2 , ... xn < in einer Urliste gegeben, wobei xi der Merkmalswert der statistischen Einheit ei darstellt. Wir haben es also mit univariaten Daten zu tun.
Zur Untersuchung dieser Daten gibt es - abhängig von der Länge n der Datenreihen und dem Typ der Daten - ganz
unterschiedliche Methoden.
Die wichtigsten, in diesem Kapitel untersuchten Methoden, sind ...
† die graphischen Darstellungen;
† die tabellarischen Darstellungen; sowie
† die Berechnung von Masszahlen
... von solchen Datenreihen.
Bei Experimenten mit sehr vielen unterschiedlichen Merkmalsausprägungen kann die Zahlenfülle den Blick auf das
Wesentliche verstellen.
In solchen Situationen können gut gewählte Graphiken helfen.
Wir werden im Folgenden diverse Methoden präsentieren, wie univariate möglichst anschaulich dargestellt werden
können.
Wir starten mit den einfachsten Punkteplots 8i, xi <, wo der Merkmalswert in der Reihenfolge der Beobachtungen
8x1 , x2 , ... xn < aufgetragen wird. Die Information wird auf diese Art nicht sehr anschaulich präsentiert. Als leichte
Abwandlung dieser Punkteplots können auch an Stelle der Punkte (oder zusätzlich zu den Punkten) senkrechte Linien
(Stabdiagramm) eingetragen werden.
Eine etwas bessere Darstellung resultiert, wenn man an Stelle der Urliste 8x1 , x2 , ... xn < die sortierte Urliste verwendet
(was natürlich mit nominal skalierten Datenreihen nicht gemacht werden kann) und die entsprechenden Punkte
8i, xsort,i < aufträgt. Sehr einfach kann man z.B. die Grösse des Medians oder eines Quantils aus der Tabelle herauslesen.
Man sieht auch wie bei diskreten Daten der gleiche xsort,i Wert mehrmals auftreten, während bei stetigen Daten dies in
der Regel nicht der Fall ist und die xsort,i streng monoton zunehmen.
In einem nächsten Schritt wird dann quasi die Abszisse mit der Ordinate vertauscht und wir verwenden eine Darstellung, in der zu jedem xsort,i die entsprechende (absolute) Häufigkeit ni (d.h. 8xsort,i , ni < )oder relative Häufigkeit hi (d.h.
8xsort,i , hi <) als Punkt aufgetragen wird. Alternativ können an Stelle der Punkte auch Linien oder Rechtecke (Säulendiagramm) eingezeichnet werden. Wenn sich die benachbarten Säulen berühren spricht man von einer Histogramm
Darstellung. Diese Darstellungen machen nur bei diskreten Daten einen Sinn, da bei stetigen Daten für praktisch alle
xsort,i die Häufigkeit gleich 1 ist.
Wir müssen also (insbesondere für stetige Daten, aber auch für diskrete Daten, die sehr viele unterschiedliche x-Werte
annehmen) die Daten in k Klassen (Intervalle) zusammenfassen. Wir haben weiterhin eine Häufigkeitsdarstellung mit
dem Unterschied, dass der Index nun nicht mehr einen gemessenen xi Wert repräsentiert, sondern ein ganzes Intervall:
d.h. 8xsort,iv , niv < oder 8xsort,iv , hiv <. Während bei den absoluten Häufigkeiten die Summe ⁄kiv=1 niv = n ergibt, liefern die
52
Skript Statistik und Stochastik
relativen Häufigkeiten eine normierte Darstellung: d.h. ⁄kiv=1 hiv = 1 und jedes hiv die Wahrscheinlichkeit repräsentiert,
einen Wert im Intervall iv zu finden.
Es gibt jedoch noch eine dritte Darstellungsmöglichkeit mit den sogenannten empirischen Dichten fiv , die insbesondere bei Histogrammdarstellungen, die Intervalle ungleicher Breite beinhalten, angewendet wird, bei der die relativen
hiv
Häufigkeiten hiv noch durch die Breite biv jeden Intervalls geteilt werden: d.h. fiv = ÅÅÅÅ
ÅÅÅ . In diesem Fall entspricht das
biv
Produkt aus fiv und biv der Wahrscheinlichkeit, einen Wert im Intervall iv zu finden.
Als letzten Schritt führen wir noch eine Summation der Häufigkeiten durch, was uns auf die Darstellung der Verteilung bzw. der Summenhäufigkeit führt. In diesem Fall werden die Paare 8xiv , ⁄ivj=1 hi < als Punkte, in der Histogrammdarstellung oder als Polygonzug dargestellt.
Die graphischen Darstellungen vermögen anschaulich einen Eindruck über die Verteilung der Daten zu vermitteln,
über ihre Symmetrie, Schiefe und Gipfligkeit.
Oft ist jedoch der Wunsch vorhanden, an Hand von wenigen Zahlen die Verteilung des Merkmals zu charakterisieren. Solche
Zahlen heissen Masszahlen oder Parameter einer Verteilung. Sie beschreiben zumeist entweder die Lage (d.h. die
durchschnittliche Grössenordnung der Merkmalswerte) oder die Streuung (d.h. wie nah sie beieinander liegen) und Form der
Verteilung (d.h. ob sie symmetrisch oder unsymmetrisch verteilt sind).
Wie schon bei den graphischen Darstellungen gibt es auch hier für die unterschiedlichen Skalierungen der Daten
(Nominalskala, Ordinalskala, Metrische Skala) unterschiedliche Methoden.
Wir werden in diesem Abschnitt verschiedene, häufig gebrauchte Masszahlen kennenlernen.
Graphische Darstellungen
Einleitung
In diesem Abschnitt untersuchen wir die verschiedenen Möglichkeiten der graphischen und tabellarischen Darstellung
von Datenreihen.
Wir behandeln in diesem Abschnitt zur Veranschaulichung kurze diskrete, lange diskrete und lange stetige
Datenreihen.
Diese Datenreihen seien folgendermassen spezifiziert.
Diskrete Datenreihe (n klein)
Bei dieser Datenreihe erzeugen wir eine Datenreihe der Länge 20, deren Werte einer Binomialverteilung mit n = 5 und
p = 0.6 entnommen sind. Der Wertebereich dieser Verteilung ist das Intervall @0, nD.
8
6
4
2
1
2
3
4
5
6
Diese Datenreihe steht repräsentativ für nominal und ordinal skalierte Daten.
53
Skript Statistik und Stochastik
Diskrete Daten (n gross: 1000)
Bei dieser Datenreihe erzeugen wir eine Datenreihe der Länge 1000, deren Werte einer Binomialverteilung mit
n = 100 und p = 0.5 entnommen sind. Der Wertebereich dieser Verteilung ist das Intervall @0, nD.
80
60
40
20
30
40
50
60
70
80
Diese Datenreihe steht ebenfalls repräsentativ für nominal und ordinal skalierte Daten. Auf Grund der grossen Anzahl
von Daten sind jedoch andere Methoden anwendbar.
Stetige Daten (n gross: 1000)
Bei dieser Datenreihe erzeugen wir eine Datenreihe der Länge 1000, deren Werte einer Normalverteilung mit m = 50
und s = 10 entnommen sind. Hier werden die relativen Häufigkeiten (d.h. normiert) der gerundeten (d.h. in Intervalle
der Breite 1 eingeteilten) Daten dargestellt.
0.05
0.04
0.03
0.02
0.01
30
40
50
60
70
80
Die in diesem Beispiel erzeugte Datenreihe hat 18.4392 als kleinsten und 89.6249 als grössten Wert.
8i, xi <
Die einfachste Darstellung dieser Datenreihen ist sicherlich, wenn man die gemessenen Werte der Reihe nach als Punkte 8i, xi <,
Stämme oder Säulen im Koordinatensystem einträgt. In der Abszisse wird der Index (der Messreihe) und in der Ordinate der
(gemessene) Merkmalswert eingetragen.
Wie die untenstehenden Plots zeigen, ist es jedoch sehr schwierig einen detaillierten Eindruck über die Verteilung zu
bekommen.
Diskrete Daten (n klein)
In einem Stabdiagramm (hier mit Symbol) wird zusätzlich zu jedem Punkt 8i, xi < eine senkrechten Linie eingetragen.
MultipleListPlot@xBDk, SymbolShape → StemD;
54
Skript Statistik und Stochastik
5
4
3
2
1
5
10
15
20
Diskrete Daten (n gross)
In einem Plot 8i, xi < werden alle beobachteten Messwerte xi gegen den Index i aufgetragen.
Man sieht ungefähr, wo sich die Daten häufen. Eine zuverlässig Angabe eines mittleren Wertes oder anderer Grössen
ist jedoch schwierig.
ListPlot@xBD, PlotRange → AllD;
65
60
55
50
45
40
200
400
600
800
1000
Es ist auch möglich, die einzelnen Punkte miteinander zu verbinden. Dadurch sieht man die Verteilung etwas besser.
ListPlot@xBD, PlotRange → All, PlotJoined → TrueD;
65
60
55
50
45
40
200
400
600
800
1000
Stetige Daten (n gross)
Bei stetigen Daten und vielen Beobachtungen unterscheidet sich ein Punkteplot nicht allzusehr von einem Punkeplot
bei diskreten Daten.
ListPlot@xND, PlotRange → AllD;
55
Skript Statistik und Stochastik
90
80
70
60
50
40
30
200
400
600
800
1000
8i, xsort,i <
Die im voranstehenden Abschnitt untersuchten xi waren nicht sortiert. Deshalb springen die xi von Beobachtung zu
Beobachtung in Richtung der Ordinate auf und ab.
Wenn die Daten xi sortiert werden und dann die Punkte 8i, sortierte xi < einzeichnet, dann erhält man eine gleichmässige Zunahme der xi Werte.
Diskrete Daten (n klein)
Bei wenigen Daten sieht man die einzelnen Datenpunkte sehr gut. Man sieht:
† es gibt nur diskrete Ordinatenwerte
† mehrere Beobachtungen können den gleichen Wert liefern
† es gibt keinen Datenpunkt mit dem Wert xi = 1
† es gibt 3 Datenpunkte mit dem Wert xi = 2
† es gibt 4 Datenpunkte mit dem Wert xi § 2
† etc.
5
4
3
2
1
5
10
15
20
Diskrete Daten (n gross)
Bei sehr grossen Datenreihen können die einzelnen Punkte nicht mehr aufgelöst werden, sie verschmelzen zu einer
Linie.
Ansonsten ist die Interpretation gleich wie bei wenig Daten.
Mit einfachen Mitteln kann beispielsweise der (Unter)Median der Verteilung bestimmt werden: Man nimmt den
mittleren Index (500) und finden das entsprechende x500 .
56
Skript Statistik und Stochastik
65
60
55
50
45
40
200
400
600
800
1000
Stetige Daten (n gross)
Bei stetigen Daten liefert in der Regel jede Beobachtung einen anderen Wert (v.a. wenn nicht allzustark gerundet wird).
Dies führt dazu, dass die Abstände zwischen den eingetragenen Ordinatenwerten (xi+1 - xi ) beliebige stetige Werte
annehmen können. Die eingetragenen Werte steigen deshalb (zumeist) streng monoton.
Aus einer solchen Graphik kann man auch auf relative einfache Art und Weise den Median finden.
90
80
70
60
50
40
30
200
400
600
800
1000
Häufigkeitsfunktionen: 8xsort,i , ni <, 8xi , hi <
In den 8i, xi,sortierte<- Plots kann man gut gesehen, wo sich die xi Werte häufen.
Eine noch bessere Darstellung erlaubt die Graphik, in der man in der Abszisse die xi und in der Ordinate die absolute
Häufigkeit ni dieser xi Werte aufträgt. Diese ni werden auch als absolute Häufigkeiten oder kurz als Häufigkeit
bezeichnet. Es gilt: ⁄ni=1 ni = n. Diese Darstellung zeigt für diskrete Daten sehr schön, wo und wie sich die xi Werte
verteilen.
ni
Wenn diese absoluten Häufigkeiten durch n geteilt werden, dann erhält man die relativen Häufigkeiten: hi = ÅÅÅÅ
Å . Die
n
n
Summe der hi ergibt 1: ⁄i=1 hi = 1. Die relativen Häufigkeiten sind also normiert.
Eine Abbildung, die einem xi das hi zuordnet, wird auch Häufigkeitsfunktion H@xD (englisch Frequency Distribution) genannt.
H@xD ist eine Kurve, die nicht nur zeigt, wo sich die meisten Beobachtungen befinden, sondern auch welche Form
(symmetrisch, schief, gipflig) die Verteilung hat.
Im Folgenden kann in den meisten Darstellungen statt ni auch hi verwendet werden. Der Einfachheit halber wird
jeweils nur eines dargestellt.
Die 8xi , nxi < Darstellung kann auch sehr einfach aus dem 8i, xi,sortiert<- Punkteplot abgeleitet werden, indem die einzelnen Punkte nach links gegen die Ordinate verschoben werden und anschliessend die Abszisse und Ordinate miteinander vertauscht werden.
57
Skript Statistik und Stochastik
Die 8xi , nxi < oder 8xi , hxi < Darstellung eignet sich jedoch nicht gut bei diskreten Verteilungen mit vielen unterschiedlichen Werten, da dann - trotz grossem n - jedes xi nur wenige Male vorkommen kann und deshalb grosse Schwankungen in benachbarten nxi auftreten können.
Die 8xi , nxi < oder 8xi , hxi < Darstellung eignet sich auch nicht bei stetigen Verteilungen, da - wie schon ausgeführt - für
die stetigen Verteilungen die Häufigkeit für jedes xi gleich 1 wäre.
In beiden Fällen kann eine optimalere Darstellung erreicht werden, wenn mehrere xi -Werte (bei diskreten Verteilungen) oder x-Intervalle jeweils zu Klassen zusammengefasst werden. Dies führt uns dann auf die wichtige Histogramm
Darstellung.
Eine Einteilung in Klassen kann aus einer Urliste beispielsweise mit folgenden Schritten vorgenommen werden:
† Sortiere die Urliste in aufsteigender Reihenfolge
† Bestimme die Intervalle.
Es gibt viele Möglichkeiten, die Intervalle festzulegen. Beispielsweise:
† Berechne die Spanne der Daten, d.h. Maximum - Minimum
† Bestimme die Anzahl k der Intervalle (Klassen, Bereiche, Bins).
Bei zu wenig Intervallen verliert man wichtige Information, bei zu vielen Intervallen wird zu wenig gemittelt.
Die optimal Anzahl hängt auch von der Verteilung der Daten ab.
è!!!!
Als Faustregel gilt k = n .
Spanne
† Bestimme die Intervallbreite als ÅÅÅÅÅÅÅÅkÅÅÅÅÅÅÅÅÅ
Man kann auch einen grösseren Bereich als die Spanne abdecken. Ausserdem ist es möglich, Intervalle
unterschiedlicher Breite zu wählen.
Maximum-Minimum
† Bestimme alle k + 1 Intervallgrenzen gi : z.B. gi = Minimum + Hi - 1L ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ " i = 1, ... k + 1
k
† Zähle die Anzahl Beobachtungen hi , die in jedes Intervall @gi , gi+1 @ fallen.
Achtung bei den Intervallgrenzen: jeder Wert darf nur einmal gezählt werden: die untere Intervallgrenze gi zählt
zum Intervall die obere Grenze gi+1 demnach nicht (da sie zum nächsten Intervall gehört), d.h. gi § x  gi+1 .
† Erstelle eine Tabelle der Punkte 8i, hi < für alle Intervalle i.
† Stelle diese Punkte graphisch in einem Histogramm dar.
Diskrete Daten (n klein)
Bei wenigen Daten muss keine Klasseneinteilung vorgenommen werden und man kann die Daten direkt als Stammdiagramm ...
8
6
4
2
1
2
3
4
5
... , in einem Säulendiagramm (englisch Barchart) oder in einem Kreisdiagramm (Kuchendiagramm , englisch Piechart) darstellen.
In einem Säulendiagramm wird für jeden xi - Wert eine Säule der Höhe nxi oder hxi eingetragen.
58
Skript Statistik und Stochastik
8
6
4
2
0
1
2
3
4
5
In einem Kreisdiagramm entsprechen die Winkel bzw. Flächen der Kreissektoren der einzelnen xi -Werte den Häufigkeiten ni
oder hi .
Diese Darstellung eignet sich jedoch nicht für sehr grosse Datenmengen, da dann die einzelnen Sektoren zu klein
würden.
2
3
0
5
4
Bei kleinen Datenmengen können die 8xi , nxi < oder 8xi , h xi < Werte auch direkt in einer Tabelle dargestellt werden.
xi
nhi
0
1
1
0
2
3
3
8
4
6
5
2
Diskrete Daten (n gross)
Diese Darstellung ist analog zur im letzten Abschnitt diskutierten Darstellung bei kleinen Datenreihen.
Für jeden xi Wert wird die Häufigkeit bestimmt. In unserem Beispiel erhalten wir die folgenden 8xi , nxi < Werte:
8834,
843,
850,
858,
1<, 836, 1<, 837, 2<, 838, 6<, 839, 8<, 840, 9<, 841, 16<, 842, 25<,
43<, 844, 41<, 845, 35<, 846, 64<, 847, 66<, 848, 89<, 849, 64<,
87<, 851, 84<, 852, 66<, 853, 59<, 854, 55<, 855, 40<, 856, 44<, 857, 30<,
20<, 859, 15<, 860, 16<, 861, 5<, 862, 5<, 863, 1<, 864, 2<, 866, 1<<
Das heisst, dass 1x der Wert xi = 34, 35x der Wert xi = 45 etc. vorkommt.
59
Skript Statistik und Stochastik
Die graphische Darstellung führt auf:
80
60
40
20
30
40
50
60
70
80
Aus dieser Graphik kann auch einfach die Häufigkeit ni eines xi Werts herausgelesen werden. Beispielsweise beträgt
für den Wert xi = 45 die Häufigkeit ni = 35.
Im Folgenden haben wir die obigen Daten in Klassen zusammengefasst, wobei die Klassengrenzen als 834, 38, ... 66<
gewählt wurden. Die Häufigkeiten wurden über der Klassenmitte eingetragen. Es muss beachtet werden, dass n
Intervalle zu n + 1 Intervallgrenzen führen. Die Säulendarstellung ergibt:
300
250
200
150
100
50
32 36 40 44 48 52 56 60 64 68
Diese Verteilung könnte auch in einem Histogramm (statt einem Säulendiagramm) dargestellt werden. Dies wird im
nächsten Abschnitt mit stetigen Daten durchgeführt.
Stetige Daten (n gross)
Die Daten unseres Beispiels (mit 1000 Beobachtungen) haben einen Minimalwert von rund 18.43 und einen Maximalwert von rund 89.62.
Wir können beispielsweise den Bereich auf das ganze Intervall [0,100] festlegen und darin 20 gleich breite Intervalle
wählen.
Dies führt auf die Intervallgrenzen ci von 80, 5, 10, ... 100<. Wenn wir die Werte in diesen Kategorien zählen erhalten
wir:
60
Skript Statistik und Stochastik
Intervall Mitte
relative Häufigkeit
2.5`
7.5`
12.5`
17.5`
22.5`
27.5`
32.5`
37.5`
42.5`
47.5`
52.5`
57.5`
62.5`
67.5`
72.5`
77.5`
82.5`
87.5`
92.5`
97.5`
0.`
0.`
0.`
0.001`
0.007`
0.016`
0.038`
0.086`
0.145`
0.194`
0.197`
0.144`
0.092`
0.054`
0.015`
0.008`
0.001`
0.002`
0.`
0.`
In einem Histogramm wird der Wertebereich der Daten in (nicht notwendigerweise) gleich grosse Intervalle eingeteilt und es
ni
Å ) als Ordinate
werden jeweils die Messwerte ni , die in diese Intervalle fallen, gezählt und eventuell nach Normierung (hi = ÅÅÅÅ
n
eingetragen.
Alternativ kann der Ordinatenwert auch so gewählt werden, dass die Fläche über jedem Intervall proportional zur
Wahrscheinlichkeit ist, einen Messwert in diesem Intervall zu finden.
Der Vorteil einer graphischen Darstellung ist, dass man sehr schnell sieht, wo die meisten Beobachtungen liegen.
0.2
0.15
0.1
0.05
20
40
60
80
100
Wenn der ganze Bereich von 0 bis 100 in nur 5 Intervalle eingeteilt wird, resultiert folgende Tabelle
Intervall Mitte
relative Häufigkeit
10.`
30.`
50.`
70.`
90.`
0.001`
0.147`
0.68`
0.169`
0.003`
61
Skript Statistik und Stochastik
... und folgendes Histogramm:
0.6
0.5
0.4
0.3
0.2
0.1
20
40
60
80
100
Man sieht, dass die Intervallbreite viel zu klein für eine vernünftige Darstellung ist.
Eine zum Histogramm ähnliche Darstellung ist ein Häufigkeits Polygon (englisch frequency polygon).
In einem Häufigkeits Polygon werden die Punkte 8MitteIntervall i , HäufigkeitIntervall i < in einem Koordinatensystem eingezeichnet
und miteinander verbunden.
Ein solcher Plot erscheint etwas kontinuierlicher als ein Histogramm mit seinen ¶ steilen Flanken.
Verteilungsfunktion: 8xi , ⁄ij=1 h j <
Als Ausgangspunkt für die Definition der Verteilungsfunktione dienen die bekannten absoluten oder relativen Häufigkeiten. Aus diesen wird ...
† die laufende Summe der absoluten Häufigkeiten ni,cum = ⁄ij=1 n j .
† oder die laufende Summe der relativen Häufigkeiten hi,cum = ⁄ij=1 h j .
... verwendet.
Eine Abbildung, die einem xi das ⁄ij=1 h j zuordnet, wird auch Verteilungsfunktion F@xD (empirische Verteilungsfunktion,
Summenhäufigkeitsfunktion; englisch Cumulative Frequency Distribution) genannt. F@xD ist eine Kurve, die zeigt wieviele
Datenpunkte (oder wieviel % der Datenpunkte) einen Werte haben, der kleiner als ein spezifizierter Wert ist.
Bei der Verteilungsfunktion handelt es sich um eine rechtsstetige Treppenfunktion.
Bei sehr vielen Datenpunkten können (ohne grossen Fehler durch die lineare Approximation zwischen den Datenpunkten) zur anschaulichen Darstellung einfach die Punkte 8xsort,i , i< miteinander verbunden werden, da nach der Sortierung
Bei stetigen Funktionen können einfach die Punkte 8xsort,i , ÅÅÅÅni < miteinander verbunden werden da gerade i (von total n)
Beobachtungen kleiner oder gleich xsort,i sind.
62
Skript Statistik und Stochastik
1
0.8
0.6
0.4
0.2
30
40
50
60
70
80
90
Es gilt:
† Die steile Flanke dieser Kurve zeigt den Wert an, den die meisten Punkte einnehmen.
† Am Rande (links und rechts) wird die Kurve flacher.
† Die Normierung führt dazu, dass die Ordinatenwerte der Kurve zwischen 0 und 1 liegen.
† Die Abszissenwerte umfassen alle gemessenen Werte xi .
Mehr Informationen zur Verteilungsfunktion kann auch in den Kapiteln über Verteilungen und Masszahlen gefunden
werden.
Weitere graphische Darstellungen
Box-And-Whisker Plot
Mit einem Box-And-Whisker Plot (Schachteldiagramm) kann sehr schnell ein Eindruck einer Datenreihe gewonnen werden.
Der Plot hat die Form einer Box, die die Distanz zwischen (ülicherweise) dem 25% Quantil und dem 75% Quantil umfasst.
Zusätzlich sind Querlinien beim Median und dem Minimum und Maximum (eventuell nach Ausschluss von Ausreissern)
eingezeichnet.
Der folgende Plot gilt für unsere Binomialverteilung (n gross).
65
60
55
50
45
40
35
Der folgende Plot zeigt alle drei unserer Beispielverteilungen.
63
Skript Statistik und Stochastik
80
60
40
20
0
1
2
3
Masszahlen - Nominalskala
Wir beginnen nun mit der Besprechung von Masszahlen. Wie schon bei den graphischen Darstellungen gibt es auch
hier für die unterschiedlichen Skalierungen der Daten (Nominalskala, Ordinalskala, Metrische Skala) unterschiedliche
Methoden. Wir starten hier mit den Methoden, die für nominalskalierte Daten eingesetzt werden können. Diese
Methoden gelten (natürlich) auch für ordinal und metrisch skalierte Daten.
Ebenso werden die im nächsten Abschnitt für ordinalskalierte Daten diskutierten Methoden auch für metrisch skalierte
Daten gelten.
Bei nominalskalierten Daten besitzt das Merkmal X insgesamt J verschiedene Merkmalswerte, die mit 8x1 , x2 , ... xJ <
bezeichnet seien. Für jeden Merkmalswert kann nun die absolute n j und relative h j Häufigkeit berechnet werden, mit
der der Merkmalswert x j in den Daten vorkommt. Im Folgenden jeweils für " j œ 81, 2. .. J <.
Die absolute Häufigkeit n j ist gleich der Anzahl der Daten mit x j = x j .
n
Die relative Häufigkeit h j ist definiert als ÅÅÅÅnÅjÅ und gibt den Anteil der Daten mit dem Merkmalswert x j = x j an.
Ein Merkmalswert x j heisst Modus, wenn seine Häufigkeit mindestens so gross wie die der übrigen Merkmalswerte ist, d.h.
wenn n j ¥ nk " k.Im Allgemeinen können Daten mehrere Modi aufweisen.
Es gilt:
† Eine Verteilung kann mehr als einen Modus haben.
† Eine Verteilung mit nur einem Modus heisst unimodal, mit zwei Modi heisst bimodal, dann trimodal ...
† Wenn alle Beobachtungswerte ungleich sind (z.B. bei stetigen Verteilungen), dann hat die Verteilung keinen
Modus.
† Der Modus ist das einzige Lokalisationsmass, das für nominale Daten verwendet werden kann.
Die absoluten und relativen Häufigkeiten können dazu benutzt werden, die Daten in einer Tabelle übersichtlicher
darzustellen.
Bei einer diskreten Klassierung werden die Merkmalswerte mit ihrer absoluten Häufigkeit als Folge dargestellt:
8x1 , n1 <, 8x2 , n2 <, ... 8xJ , n J <
Unter einer Häufigkeitstabelle versteht man eine Tabelle der Form:
64
Skript Statistik und Stochastik
j
1
2
...
J
Σ
ξj
ξ1
ξ2
...
ξJ
nj
n1
n2
...
nJ
n
hj
h1
h2
...
hJ
1
Nominalskalierte Daten können durch verschiedene graphische Darstellungen veranschaulicht werden. Wichtig sind
vor allem Säulendiagrammen oder Kreisdiagramme.
Masszahlen - Ordinalskala
Für Daten, deren Merkmal X (mindestens) ordinalskaliert ist, gibt es eine natürliche Ordnung. Für eine Datenreihe
8x1 , ... xn < kann man eine Verteilungsfunktion F@xD definieren.
Die Funktion F@xD mit x œ mit
»8i»xi §x<»
F@xD = HAnteil der Daten § xL = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ = S hr
n
xr §x
wird empirische Verteilungsfunktion oder auch kurz Verteilungsfunktion genannt.
Bei Vorliegen einer Urliste ermittelt man F@xD durch Abzählen der Beobachtungswerte, die kleiner oder gleich x, und
anschliessende Division durch n. Wenn diskret klassierte Daten gegeben sind, wird F@xD durch Addition der entsprechenden relativen Häufigkeiten berechnet.
Die Verteilungsfunktion hat die folgenden Eigenschaften:
† Sie ist monoton wachsend.
† Sie ist eine Treppenfunktion, d.h. stückweise konstant. Die Sprünge entstehen an jenen Stellen, die als Daten in der
Urliste vorkommen, und die Sprunghöhe an einer Stelle x = x j ist gleich der relativen Häufigkeit des Wertes x j in
der Urliste.
† Sie ist rechtsstetig, d.h. der Funktionswert an einer Sprungstelle ist gleich dem Grenzwert der Funktionswerte,
wenn man das Argument x von rechts der Sprungstelle annähert.
Wenn die Verteilungsfunktion bekannt ist, lassen sich daraus die beobachteten Merkmalswerte und ihre relativen
Häufigkeiten ermitteln.
Ein weiteres wichtiges Mass zur Beschreibung von Daten ist das Quantil und kann mit Hilfe der Verteilungsfunktion
definiert werden.
Das p-Quantil xè p der Daten ist (für 0  p  1) definiert als xè p = min 8x œ » F@xD ¥ p<
Die Funktion, die p in xè p abbildet heisst Quantilfunktion.
Das p%-Quantil (oder auch p-tes Perzentil oder p-tes Fraktil) ist jene Zahl xè p % , für die die kumulierte Verteilungsfunktion
den Wert von p% annimmt. Dies heisst, dass p% der Beobachtungen einen kleineren Wert haben als das p%-Quantil.
Wichtige Quantile tragen spezielle Namen. Beispielsweise
x
0.5
x0.25 , x0.50 , x
0.75
Median
Quartile
65
Skript Statistik und Stochastik
,x
,x
x0.2 , x
0.4
0.6
0.8
x0.1 , ... x0.9
x
, ... x
0.01
0.99
Quintile
Dezile
Perzentile
Die Quantile sind gut zu interpretieren und nützlich, um grosse Datenmengen mit vielen verschiedenen Werten zu
charakterisieren.
† Das Quantil xè 0.25 bezeichnet man als unteres Quartil, das Quantil xè 0.5 als mittleres Quartil oder Median, das
Quantil xè 0.75 als oberes Quartil.
† Der Median ist der Wert, der die unteren 50% der Daten von den oberen 50% der Daten trennt. (Siehe später mehr)
† Die Quartile xè , xè , xè
teilen die Daten in vier Blöcke, die jeweils 25% der Daten umfassen. Zwsichen dem
0.25
0.5
0.75
unteren und oberen Quartil liegen die "mittleren" 50% der Daten.
Quantile können auch berechnet werden, ohne die Verteilungsfunktion F@xD zu berechnen. In einem ersten Schritt
werden die Daten aufsteigend sortiert. Dann gilt (gemäss Mosler&Schmid):
† falls n p ganzzahlig: xè p = xn p
† andernfalls: xè p = x@n pD+1 , wo @n pD den ganzzahligen Teil von n p bezeichnet.
alternativ könnte man auch eine lineare Interpolation zwischen den Daten durchführen.
Mit dieser Definition wird immer einer der xi Werte retourniert.
Beispielsweise ist bei n = 17 das 3. Quartil:
xè 0.75 = x@n pD+1 = [email protected]+1 = x12+1 = x13
Diese Art der Quartilsbestimmung ist jedoch bei weitem nicht die einzige in der Statistik verwendete Implementation. Es gibt
mindestens zehn weitere unterschiedliche Definitionen.
In den CFA Readings wird i, der Index von x, mittels Hn + 1L q berechnet und bei nicht ganzer Zahl zwischen den
benachbarten Werten (d.h. xi und xi+1 ) interpoliert. Für obiges Beispiel würde also resultieren:
xè 0.75 = xHn+1L q = x13.5 = x13 + 0.5 Hx14 - x13 L
Masszahlen - Metrisch skalierte Daten
Für metrisch skalieren Daten können weitere Rechenoperationen ausgeführt werden.
Im Folgenden werden die wichtigsten Masszahlen, die die ganze Information einer Folge von Daten 8x1 , ... xn < in eine
einzige Masszahl komprimieren, besprochen. Diese Masszahlen machen insbesondere Aussagen über die Lage, die
Streuung und die Form der Verteilung (Asymmetrie) der Daten von metrisch skalierten Daten.
Lagemasse (Lokalisationsmasse)
⁄ni=1 xi
Das arithmetische Mittel êêx ist definiert als êêx = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ bzw. in Worten ausgedrückt als Summe der Beobachtungen geteilt
n
durch die Anzahl der Beobachtungen.
Das arithmetische Mittel ist das am häufigsten verwendete Lokalisationsmass und wird oft einfach als Mittelwert,
Durchschnitt oder Schwerpunkt der Daten bezeichnet.
Das arithmetische Mittel hat folgende wichtige Eigenschaften:
66
Skript Statistik und Stochastik
† Merkmalssumme:
⁄ni=1 xi = n êêx
† Das arithmetische Mittel liegt zwischen dem grössten und dem kleinsten Wert der Daten.
† Zentraleigenschaft: ⁄n Hx - êêx L = 0
i=1
i
Die Abweichungen der Daten vom arithmetischen Mittel heben sich gegenseitig auf.
† Verschiebung:
yi = xi + a; êêy = êêx + a
x
† Homogenität:
y = b x ; êêy = b êê
i
i
† affin-lineare Transformation:
yi = b xi + a; êêy = b êêx + a
Das arithmetische Mittel transformiert sich wie die Einzeldaten.
† Es gilt:
⁄n Hx - êêx L2 = min ⁄n Hx - c L2
i=1
i
cœ
i=1
i
Die Summe der quadratischen Abweichungen der Daten von einem festen Punkt c ist für das arithmetische Mittel
am kleinsten.
† Das arithmetische Mittel ist empfindlich auf Ausreisser.
Bei der Berechnung des arithmetischen Mittels werden alle Merkmalswerte mit dem gleichen Gewicht verwendet.
Wenn ein Wert aus der Urliste und dem Gewichtsvektor 8w1 , ... wn <, mit wi ¥ 0 und ⁄ni=1 wi = 1 gemäss der Beziehung
êêx = ⁄n w x
w
i=1 i i
berechnet wird, resultiert das sogenannte gewichtete Mittel.
Das arithmetische Mittel kann auch als gewichtetes Mittel mit dem Gewichtsvektor 8w1 , ... wn <, wo alle Gewichte den
gleichen Wert ÅÅÅÅ1n haben, verstanden werden.
Das gewichtete Mittel spielt eine wichtige Rolle in der Portfolio Analyse zur Berechnung des Total Return, wenn
unterschiedliche Gelmengen in den verschiedenen Assets investiert werden.
Auch bei market-capitalization Indizes (wie z.B. S&P 500) wird der Index als mit dem Marktwert jeder Aktie gewichtetes Mittel berechnet.
Wenn nun ein Beobachtungswert sehr weit - nach oben oder unten - von den übrigen entfernt ist, hat sein Beitrag einen
grossen Einfluss auf êêx . Das arithmetische Mittel ist nicht robust gegen sogenannte Ausreisser. Einen robusteren
Mittelwert konstruiert man, indem man die Daten trimmt, d.h. einen Anteil extremer Werte weglässt.
Das a-getrimmte Mittel hat die Formel
1
êêx = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ n-@n aD x
a
n-2 @n aD ⁄i=1+@n aD i
wobei [n a] den ganzzahligen Teil von n a bezeichnet;
wobei 0  a  0.5;
Beim a-getrimmten Mittel wird der Anteil a der Daten oben und unten in der sortierten Liste weggelassen und aus den
verbleibenden Daten der Mittelwert berechnet. Es ist robuster als der arithmetische Mittelwert.
Weitere Lokalisationsmasse sind der (schon für nominal skalierte Daten definierte) Modus (falls er eindeutig bestimmt
ist) und der (schon für ordinal skalierte definierte) Median. Sie werden der Vollständigkeit halber nochmals kurz mit
ihren Eigenschaften aufgeführt.
Der Median (auch Zentralwert genannt) ist so definiert, dass 50% der Daten grösser und 50% der Daten kleiner als der
Median sind.
Sortiert man die Beobachtungswerte der Größe nach („geordnete Stichprobe“), so ist der Median bei einer ungeraden
Anzahl von Beobachtungen der in der Mitte dieser Folge liegende Beobachtungswert.
Bei einer geraden Anzahl von Beobachtungen gibt es kein einziges mittleres Element, sondern einen ganzen Bereich.
Alle denkbaren (nicht beobachteten) Werte zwischen den beiden in der Mitte liegenden Werten sind ein Median der
67
Skript Statistik und Stochastik
Stichprobe, da für alle diese Werte obige Bedingung zutrifft. In der Statistik werden rund 10 verschiedene Definitionen für den Median angewandt. Die folgenden drei sind die gebräuchlichsten; man sollte sich jeweils im Klaren
sein, welche Definition vom benutzten Programm (Taschenrechner, Excel etc) verwendet wird:
† Untermedian: xnê2 ; diese Definition stimmt auch mit dem 0.5-Quantil xè 0.5 überein;
† Zentraler Wert: ÅÅÅÅ12 Hxnê2 + xnê2+1 L; CFA verwendet diese Definition.
† Obermedian: xnê2 + 1;
Während der Untermedian und der Obermedian mit einem Datenpunkt übereinstimmen, kann der Zentrale Wert einem
nicht vorkommenden Wert entsprechen.
Ein Vorteil des Medians ist, dass er besonders robust gegen Ausreisser ist und auch für ordinal skalierte Daten verwendet werden kann.
Ein Nachteil des Median kann sein, dass er nicht alle Beobachtungen verwendet und die Berechnung mathematisch
aufwendiger als die Berechnung des Mittelwerts ist.
Bei verhältnisskalierten Merkmalen lassen sich zwei weitere Lokalisationsmasse bilden: das harmonische und das
geometrische Mittel.
-1
n
1
Das harmonische Mittel êêx H ist folgendermassen definiert: êêx H = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅ = I ÅÅ1nÅÅ ‚ xi -1 M
nÅÅÅÅÅÅÅÅ
ÅÅÅÅ1ÅÅ
ÅÅ1ÅÅ
i=1
n
‚
i=1 xi
Das harmonische Mittel ist der Kehrwert des arithmetischen Mittels der Kehrwerte der Daten xi .
Das harmonische Mittel kann sinnvollerweise angewandt werden, wenn Verhältnisse gemittelt werden. Eine Anwendung ist z.B. die als cost-averaging bekannte Investment Strategie, in welcher eine fixe Geldsumme investiert wird. In
Preis
diesem Beispiel wird das Verhältnis ÅÅÅÅÅÅÅÅ
ÅÅ Å gemittelt.
Aktie
Beispielsweise werde CHF 1000 in zwei aufeinanderfolgenden Perioden investiert. In der ersten Periode koste die
Aktie CHF 10.00 und es können 100 Aktien gekauft werden. In der zweiten Periode koste die Aktie CHF 12.50 und es
können 80 Aktien gekauft werden. Was ist der durchschnittliche Preis der Aktie?
inv.Geld
2000
ÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅ Å = 11.11 Franken pro Aktie. Der
Der Quotient aus dem investierten Geld und der Anzahl Aktien ergibt ÅÅÅÅÅÅÅÅ
# Aktien
180
1
durchschnittlich bezahlte Preis ist in der Tat das harmonische Mittel der jeweiligen Preise: êêx H = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
1
1 ÅÅÅÅÅÅÅÅ
1 ÅÅÅÅÅ =11.11
ÅÅÅÅ2 H ÅÅÅÅ
ÅÅÅÅÅÅÅ L
10ÅÅÅ + ÅÅÅÅ
12.5
1
n
è!!!!!!!!!!!!!!!!
!
ÅÅ1ÅÅ
lnHx L
Das geometrische Mittel êêx G ist folgendermassen definiert: êêx G = x1 ... xn = H¤ni=1 xi L ÅÅnÅÅ = e n ‚i=1 i
êêêêêêêê
1
êê
n
Damit gilt auch: lnHx G L = ÅÅÅÅn ⁄i=1 lnHxi L = lnHxi L
n
Der (natürliche) Logarithmus des geometrischen Mittels ist das arithmetische Mittel der logarithmierten Daten.
Das geometrische Mittel wird vor allem bei der Berechnung von durchschnittlichen Wachstumsfaktoren und Wachstumsraten angewandt. Wenn sich z.B. das investierte Kapital pro Jahr um den Faktor 1 + Ri erhöht, dann gilt nach n
Jahren:
H1 + Rg Ln = H1 + R1 L H1 + R2 L ... H1 + Rn L
wo 1 + Rg den durchschnittlichen jährlichen Faktor darstellt und sich nach der Formel für das geometrische Mittel
berechnen lässt:
n
è!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
!
1 + Rg = H1 + R1 L H1 + R2 L ... H1 + Rn L
Wie man sieht vermittelt das geometrische Mittel einen Wert für den über mehrere Jahre erzielten durchschnittlichen
Profit. Das arithmetische Mittel hingegen konzentriert sich auf einen pro Jahr erzielten durchschnittlichen Profit. Beide
Masse können einem Investor wichtige Informationen liefern.
Skript Statistik und Stochastik
68
Im allgemeinen gilt, dass die Differenz zwischen dem arithmetischen und geometrischen Mittel zunimmt, wenn die
Variabilität der Daten zunimmt.
Das arithmetische, harmonische und geometrische Mittel gehören zur Familie der Potenzmittel, die folgendermassen definiert
ÅÅ1pÅÅ
n
sind: êêx p = I ÅÅ1nÅÅ ‚ xi p M .
i=1
Es gilt:
limes êêx p
pØ-¶
= min 8x1 , ... xn <
êêx
-1
= harmonisches Mittel
limes êêx p
= geometrisches Mittel
êêx
1
= arithmetisches Mittel
limes êêx p
= max 8x1 , ... xn <
pØ0
pØ+¶
Man kann zeigen, dass immer gilt: êêx H § êêxêG § êêx
Das Gleichheitszeichen gilt, wenn alle xi gleich sind.
Streuungsmasse
Eine weitere Aufgabe der beschreibenden Statistik ist, Aussagen über die Streuung (englisch Dispersion) der Daten zu
machen. Es soll beschrieben werden, wie weit die Daten auf der Merkmalsachse x voneinander entfernt liegen oder um
ein geeignet definiertes Zentrum streuen.
Die wichtigsten Streuungsmasse sind die Standardabweichung und die Varianz.
Die Varianz s2 ist definiert als: s2 = ÅÅÅÅ1n ⁄ni=1 Hxi - êêx L2 = ÅÅ1nÅÅ ⁄ni=1 xi 2 - êêx2
Es gilt für die Varianz:
† Die Varianz und die Standardabweichung sind genau dann gleich 0, wenn alle Merkmalswerte xi den gleichen
Wert haben.
† Die Gültigkeit des Ausdrucks ganz rechts lässt sich folgendermassen zeigen:
= ÅÅÅÅ1n ⁄ni=1 Hxi - êêx L2 = ÅÅÅÅ1n ⁄ni=1 Hxi 2 - 2 xi êêx + êêx 2 L
s2
= ÅÅÅÅ1n H⁄ni=1 xi 2 - 2 êêx ⁄ni=1 xi + ⁄ni=1 êêx 2 L = ÅÅÅÅ1n H⁄ni=1 xi 2 - 2 êêx n êêx + n êêx 2 L
= ÅÅ1nÅÅ ⁄ni=1 xi 2 - êêx 2
Diese Formel verwendet nichtzentrierte Summanden und kann bei grossen Werten zu Rundungsfehlern führen.
† Man kann die Varianz auch ohne Verwendung des Mittelwerts berechnen (ohne Beweis):
1
n
s2 = ÅÅÅÅ
ÅÅÅÅÅ n
Hxi - x j L2
2 n2 ⁄i=1 ⁄ j=1
1
† Vielfach wird für die Varianz auch die Formel ÅÅÅÅ
ÅÅÅÅÅÅ n Hxi - êêx L2 verwendet: d.h. n - 1 statt n. Diese Formel ist
n-1 ⁄i=1
dann anzuwenden, wenn der Mittelwert der Daten êêx nicht gegeben, sondern vorgängig auch aus der Stichprobe
(den Daten xi ) berechnet werden muss. Dazu mehr im Kapitel über induktive Statistik.
† Bei einer affin-linearen Transformation (d.h. yi = a + b xi ) mit reellen a und b gilt: s2Y = b2 s2X und sY = †b§ s X
Die Varianz und die Standardabweichung werden demnach von einer Verschiebung um a nicht beeinflusst. Der
69
Skript Statistik und Stochastik
Faktor b jedoch geht als Faktor mit seinem Quadrat in die Varianz und mit seinem Absolutbetrag in die Standardabweichung ein.
êê - cL2 .
† Für die Varianz gilt der folgende Verschiebungssatz: ÅÅÅÅ1n ⁄ni=1 Hxi - cL2 = s2 + Hx
Man erkennt (wiederum), dass das arithmetische Mittel die Summe der quadrierten Abweichungen minimiert.
† Die Varianz hat die gleiche Einheit wie x2 .
Die Standardabweichung s ist definiert als die Wurzel aus der Varianz: s =
è!!!!!
!
s2
Es gilt für die Standardabweichung:
† Im Gegensatz zur Varianz hat die Standardabweichung die gleiche Einheit wie x und ist deshalb etwas einfacher zu
interpretieren.
† Mit Hilfe der Tschebyscheff-Ungleichung der Wahrscheinlichkeitsrechnung kann man zeigen, dass (bei jeder
Verteilung)
- mindestens 75% der Daten im Intervall D êê
x - 2 s, êêx + 2 s@
- mindestens 88.88% der Daten im Intervall D êêx - 2 s, êêx + 2 s@
liegen
Vielfach wird für die Varianz und die Standardabweichung auch s2X und s X geschrieben, um herauszustreichen, dass
sich das Streumass auf das Merkmal X bezieht.
Dadurch dass in die Berechnung der Varianz und der Standardabweichung quadrierte Abstände eingehen, haben
Ausreisser einen grossen Einfluss auf deren Wert. Um den Einfluss der Ausreisser zu minimieren kann - ähnlich wie
bei den Lokalisationsmassen - eine a-getrimmte Varianz oder Standardabweichung definiert werden. Bei diesen
werden der obere und untere a Anteil der Daten in der Berechnung nicht berücksichtigt. Bei der folgenden Definition
wird wiederum vorausgesetzt, dass die Daten aufsteigend sortiert sind.
1
Die a-getrimmte Varianz ist definiert als: s2a = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ n-@n aD Hxi - êêx a L2 . Analog ist die a-getrimmte
n- 2@n a D ⁄i=1+@n aD
è!!!!!
!
Standardabweichung sa = s2a definiert.
Analog wie bei den Lokalisationsmassen gibt es eine ganze Reihe von weiteren Massen für die Streuung.
Die mittlere absolute Abweichung d vom Mittelwert ist definiert als d = ÅÅÅÅ1n ⁄ni=1 †xi - êêx §.
Die mittlere absolute Abweichung vom Mittelwert (englisch: mean absolute deviation) verwendet alle Beobachtungen
und ist relativ einfach zu berechnen. Sie ist jedoch (wegen des Knicks der Funktion † ...§) mathematisch schwierig zu
behandeln.
Die mittlere absolute Abweichung d vom Median ist definiert als d = ÅÅ1nÅÅ ⁄ni=1 †xi - xè 0.5 §.
Sie hat die hat die Minimumeigenschaft d = Min ÅÅÅÅn1 †xi - x j §.
aœ
1
n
Ginis mittlere Differenz ist definiert als D = ÅÅÅÅ
ÅÅ n
†x - x j §
n2 ⁄i=1 ⁄ j=1 i
Wie bei der Varianz werden hier die Abstände zwischen je zwei Beobachtungen gemittelt. Allerdings werden statt der
quadrierten die absoluten Abstände genommen. D wird auch verwendet bei der Berechnung des Gini Koeffizienten,
des am meisten gebräuchlichen Disparitätsindex (siehe später).
Weiters gibt es einige Streumasse, die mit Quantilen in Zusammenhang stehen.
70
Skript Statistik und Stochastik
Der Quartilsabstand (oder Interquartilsabstand) Q ist die Differenz zwischen dem oberen und unteren Quartil:
Q = xè 0.75 - xè 0.25 .
Q ist die Spanne, die die mittleren 50% der Daten umfasst. Er ist besonders robust gegen Ausreisser, da die Werte im
oberen und unteren Viertel keine Rolle spielen.
Die Spannweite R ist die Differenz zwischen dem grössten und kleinsten Wert: R = Max@xi D - Min@xi D.
Die Spannweite (englisch Range) wird besonders stark von Ausreissern beeinflusst. Sie ist jedoch sehr einfach zu
berechnen, indem sie nur zwei Informationen nutzt.
êêê 2
S êêêHXi -X L
"Xi X
n* -1
Die Semivariance SV ist definiert als SV = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ , wobei n* der Anzahl Messungen entspricht, die kleiner als der
Mittelwert sind. Semideviation (oder Semistandard Deviation) entsprechen der Wurzel aus der Semivariance.
Vielfach wird die Varianz oder Standardabweichung der Returns eines Assets als Mass für das Risiko interpretiert. Die
Varianz und die Standardabweichung berücksichtigen jedoch die Abweichungen über und unter dem Mittelwert. Aus
diesem Grund haben Analysten die Semivarianz, Semideviation und verwandte Streumasse entwickelt, die nur auf die
downside risk fokussiert sind.
In der Praxis kann es auch vorkommen, dass man vor allem an den Abweichungen nach unten von einem anderen Wert
als dem Mittelwert interessiert ist. Dies führt auf die Definition ...
S HXi -BL2
" X B
i
Die Target Semivariance ist definiert als ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
n* -1
... wo nur Werte Xi  B berücksichtigt werden.
Bei symmetrischen Verteilungen führen die Verwendung von Varianz und Semivarianz praktisch zum gleichen
Ergebnis. Bei unsymmetrischen Verteilungen resultieren jedoch unterschiedliche Bewertungen für das Risiko.
Wir haben festgestellt, dass die Standardabweichung einfacher zu interpretieren ist als die Varianz, da sie die gleiche
Einheit wie die Beobachtung hat. Trotzdem gibt es Situationen, in denen es schwierig ist zu interpretieren, was der
(absolute) Wert der Standardabweichung auch wirklich bedeutet: insbesondere wenn verschiedene Datensätze miteinander verglichen werden sollen, die stark unterschiedliche Mittelwerte haben oder die gar unterschiedliche Einheiten
tragen. In solchen Situationen kann ein relatives (einheitenloses) Streuungsmass, der Variationskoeffizient (englisch:
coefficient of variation), nützlich sein.
Der Variationskoeffizient CV ist definiert als der Quotient aus der Standardabweichung und dem arithmetischen Mittelwert:
d.h. CV = ÅÅÅÅêêxsÅ .
Wenn die Beobachtungen z.B. Returns sind, dann misst
der Variationskoeffizient die Höhe des Risikos (Standardabweiêê
1
chung) pro ReturnEinheit. Umgekehrt misst ÅÅÅÅ
ÅÅÅÅÅ = ÅÅÅÅxs den Return pro RisikoEinheit. Beispielsweise hat ein Portfolio
CV
1.19
mit einem monatlichen Return von 1.19% und einer Standardabweichung von 4.42% ein CV-1 von ÅÅÅÅ
ÅÅÅÅÅÅ = 0.27. Das
4.42
bedeutet, dass jedes % Standardabweichung einen Return von 0.27% repräsentiert.
Ein genaueres Mass für die Return-Risiko Beziehung berücksichtigt, dass es einen risikofreien (d.h. StandardabweiReturn-riskfree Return
chung = 0) Return gibt. Dies führt auf das wichtige Sharpe Ratio = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ .
s
Zum Abschluss wollen wir noch die Chebyshev Ungleichung erwähnen. In ihr wird die Standardabweichung als Mass
für die Streuung verwendet.
71
Skript Statistik und Stochastik
Die Chebyshev Ungleichung besagt, dass der Anteil der Beobachtungen, die innerhalb von k Standardabweichungen vom
1
arithmetischen Mittel liegen, mindestens 1 - ÅÅÅÅ
ÅÅ (" k>1) beträgt.
k2
Wenn wir Informationen über die Verteilung haben, können wir in der Regel viel engere Intervalle (als das durch die
Chebyshev Ungleichung angegebene) angeben. Die Wichtigkeit dieser Ungleichung rührt jedoch daher, dass sie für
jede Verteilung - unabhängig davon wie die Daten verteilt sind - gilt.
Formmasse
Der arithmetische Mittelwert und die Varianz beschreiben nicht immer genügend genau die Verteilung der Beobachtungen. Beispielsweise werden bei der Berechnung der Varianz die Abweichungen vom Mittelwert quadriert, weshalb wir
nicht wissen, ob die grossen Abweichungen ein positives oder negatives Vorzeichen haben.
Wir müssen deshalb neben den Lokalisations- und Streuungsmassen weitere Masse einführen, um weitere Eigenschaften einer Verteilung (mit einer Zahl) zu beschreiben. Ein wichtiger Punkt ist die Symmetrie von Verteilungen. Bei
einer symmetrischen Verteilung ist jede Seite der Verteilung (um den Mittelwert) ein Spiegelbild der anderen Seite.
Eine nichtsymmetrische Verteilung kann mit Hilfe der sogenannten zentralen Momente definiert weden.
1
Das r-te zentrale Moment ist definiert als mr = ÅÅÅÅ
Hx - êêx Lr
n ⁄i i
Wichtig sind vor allem das 2. (Varianz), das 3. (Schiefe) und das 4. (Wölbung) zentrale Moment.
m3
xi -x
Die Schiefe S (englisch Skewness, Skew) ist definiert als S = ÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅ1n ‚ I ÅÅÅÅÅÅÅÅ
ÅÅÅÅ M , wobei m3 das dritte zentrale Moment ist.
s3
s
i
êê 3
Für eine Stichprobe verwendet man S =
êê 3
xi -x
n
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅ
I ÅÅÅÅÅÅÅÅ
ÅÅÅÅ M .
Hn-1L Hn- 2L ‚i
s
Es gilt:
† Die Schiefe ist ein (einheitenloses) Mass für die Symmetrie der Wahrscheinlichkeitsverteilung zum Mittelwert.
† Eine symmetrische Verteilung hat die Schiefe 0. Eine Schiefe von 0.5 wird (bei mehr als 100 Datenpunkten) als
gross betrachtet.
† Ist die Schiefe > 0, so überwiegen die Summanden mit Hx - êêx L3 > 0, andernfalls umgekehrt.
i
† Ist die Schiefe > 0, wird die Verteilung als rechtsschief (linkssteil), andernfalls als linksschief (rechtssteil)
bezeichnet.
† Eine rechtsschiefe Verteilung hat viele kleine Abweichungen nach unten und wenige grosse Abweichungen nach
oben (und damit einen langen Schwanz auf der rechten Seite).
† Es gilt für eine rechtsschiefe unimodale Verteilung: Modus  Median  Mittelwert
Es gilt für eine linksschiefe unimodale Verteilung: Mittelwert  Median  Modus
Für Investoren ist eine rechtsschiefe unimodale Verteilung interessant, da der Mittelwert (der Returns) über dem
Median liegt. Wenige grosse Gewinne überwiegen im Vergleich mit den vielen kleinen Verlusten.
† Da die Normalverteilung die Schiefe Null hat (sie ist immer symmetrisch zum Mittelwert), ist die Schiefe auch ein
geeignetes Werkzeug, um eine beliebige Verteilung mit der Normalverteilung zu vergleichen.
† Da die Schiefe mit den standardisierten Daten definiert wird, ist sie invariant gegenüber Transformationen des
Nullpunkts und der Masseinheit (d.h. xi Ø a + b xi ).
† Die Schiefe hat den Nachteil, dass sie nicht normiert ist, und beliebig grosse positive und negative Werte annehmen kann.
† Die Schiefe hat den Nachteil, dass sie empfindlich auf Ausreisser reagiert.
72
Skript Statistik und Stochastik
n
† Für eine Stichprobe ist die Stichprobenstandardabweichung s und der Faktor ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ (statt ÅÅÅÅ1n ) zu verwenden:
Hn- 1L Hn- 2L
xi -x
n
Schiefe = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ
H ÅÅÅÅÅÅÅÅ
ÅÅÅÅ L . Für grosse n führt dies auf den gleichen Wert.
Hn- 1L Hn- 2L ‚i
s
êê 3
Hx0.75 -x0.5 L-Hx0.5 -x0.25 L
Die Quartilsschiefe wird definiert als ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ Å
xè
-xè
è
è
è
0.75
è
0.25
Für die Quartilsschiefe gilt:
† Sie ist weniger empfindlich auf Ausreisser als die Schiefe.
† Sie ist ausserdem normiert und auf das Intervall @-1, 1D beschränkt.
† Sie ist invariant gegenüber Transformationen des Nullpunkts und der Masseinheit (d.h. xi Ø a + b xi ).
† Die Berechnung der Quartilsschiefe ist einfach und benötigt nur drei Quartile.
† Sie beträgt bei einer symmetrischen Verteilung gleich 0.
Die Schiefe ist ein Mass für die Abweichung einer Verteilung von der Symmetrie, wie sie beispielsweise für die
Normalverteilung gilt. Eine Verteilung kann jedoch noch in einer anderen Weise von einer Normalverteilung abweichen. Es können z.B. mehr Beobachtungen (als in der Normalverteilung) in der Nähe des Mittelwerts (d.h. hoher
Peak) und gleichzeitig mehr Beobachtungen weit entfernt vom Mittelwert (d.h. fetter Schwanz) haben. Um diese
Charakteristik zu beschreiben wird die Wölbung verwendet.
m4
xi -x
ÅÅ Å = ÅÅ1nÅÅ ‚ I ÅÅÅÅÅÅÅÅ
Die Kurtosis oder Wölbung ist definiert als: ÅÅÅÅ
ÅÅÅÅ M , wobei m4 das vierte zentrale Moment ist.
s4
s
i
êê 4
m4
xi -x
Die Excess Kurtosis oder Excess ÅÅÅÅ
ÅÅ Å - 3 = ÅÅÅÅ1n ‚ I ÅÅÅÅÅÅÅÅ
ÅÅÅÅ M - 3 ist die Kurtosis relativ zur Normalverteilung.
s4
s
i
êê 4
nHn+1L
xi -x
3 Hn-1L
Für eine Stichprobe verwendet man für die Excess Kurtosis ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ
I ÅÅÅÅÅÅÅÅ
ÅÅÅÅ M - ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ .
Hn- 1L Hn- 2L Hn- 3L ‚i
Hn-2L Hn-3L
s
êê 4
2
Es gilt:
† Die Standard Normalverteilung hat die Wölbung 3. Die Excess Kurtosis beschreibt die Abweichung des Verlaufs
der gegebenen Wahrscheinlichkeitsverteilung zum Verlauf einer Normalverteilung.
† Ist die Excess Kurtosis einer Verteilung gross, so kommt ein höherer Anteil der Varianz von Ausreissern als bei
einer Verteilung mit geringer Excess Kurtosis.
† Eine Verteilung mit Excess Kurtosis < 0 heisst flachgipflig (platycurtic).
Eine Verteilung mit Excess Kurtosis = 0 heisst normalgipflig (mesocurtic).
Eine Verteilung mit Excess Kurtosis > 0 heisst steilgipflig (leptocurtic).
† Eine Excess Kurtosis von 1.0 wird (bei mehr als 100 Datenpunkten) als gross betrachtet.
† Da die Wölbung mit den standardisierten Daten definiert wird, ist sie invariant gegenüber Transformationen des
Nullpunkts und der Masseinheit (d.h. xi Ø a + b xi ).
† Die meisten Return Verteilungen sind leptocurtic. Wenn diese fetten Schwänze bei der statistischen Analyse nicht
berücksichtigt werden, wird die Wahrscheinlichkeit eines sehr guten oder sehr schlechten Ausgangs unterschätzt.
Zentrierung und Standardisierung
Wichtige Rechenoperationen sind die Zentrierung und Standardisierung. Sie werden verwendet, um Daten von zwei
(oder mehr) Merkmalen zu vergleichen. Will man von deren unterschiedlicher Lage absehen und nur die übrigen
Aspekte wie Streuung und allgemeine Form der Verteilung berücksichtigen, so untersucht und vergleicht man die
zentrierten Daten.
Zentrierte Daten werden gebildet, indem der arithmetische Mittelwert abgezogen wird: xi Ø xi - êêx
73
Skript Statistik und Stochastik
Will man zusätzlich auch noch von der unterschiedlichen Streuung absehen, werden standardisierte Daten verwendet.
êê
xi -x
Standardisierte Daten werden gebildet, indem man die zentrierten Daten durch die Standardabweichung teilt: xi Ø ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
s
x
Wichtige Masszahlen wie Schiefe und der Korrelationskoeffizient sind so definiert, dass sie nur von den standardisierten Daten abhängen. Sie beschreiben Aspekte der Daten, die nichts mit ihrer Lage und ihrer Streuung zu tun haben.
èè
Additionssätze für x und s2
Wir wollen in diesem Abschnitt den Fall untersuchen, dass die Grundgesamtheit G in J Teilgesamtheiten
G1 , G2 , ... GJ zerfalle. Für diese J Grundgesamtheiten seien die Mittelwerte êêx 1 , êêx 2 , ... êêx J sowie die Varianzen
s21 , s22 , ... s2J bekannt, wobei die Teilgesamtheiten n1 , n2 , ... nJ Daten enthalten.
Es gilt (ohne Herleitung)
n
Der Mittelwert der Grundgesamtheit beträgt: êêx = ⁄ Jj=1 êêx j ÅÅÅÅnÅjÅ .
Die Varianz der Grundgesamtheit führt auf den sogenannten Varianzzerlegungssatz und beträgt:
n
nj
êê - êêxL2 ÅÅÅÅ
s2 = ⁄ Jj=1 s2j ÅÅÅÅnÅjÅ + ⁄ Jj=1 Hx
ÅÅ = s2 +s2
´¨¨¨¨¨¨¨¨¨¨¨¨≠¨¨¨¨¨¨¨¨¨¨Æ ´¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨j¨≠¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨n¨¨Æ int ext
s2int
s2ext
Die Gesamtstreuung besteht demnach aus zwei Teilen:
† der internen Varianz: d.h. gewichtetes Mittel aus den Streuungen der Teilgesamtheiten.
s2int = 0 heisst: in jeder Teilgesamtheit sind alle Merkmalswerte gleich.
† sowie der externen Varianz: d.h. gewichtetes Mittel der quadratischen Abweichungen der Mittelwerte der Teilgesamtheiten vom Gesamtmittel.
s2ext = 0 heisst: alle Teilgesamtheiten haben den gleichen Mittelwert êêx j = êêx .
Mit Hilfe des Varianzzerlegungssatz kann eine weitere Masszahl definiert werden.
s2
Das Bestimmtheitsmass B ist definiert als B = ÅÅÅÅsext
Å2ÅÅÅÅ
Es gibt den Anteil der externen Streuung an der Gesamtstreuung. Dieser Anteil ist auf die Einteilung der Grundgesamtheit in
Teilgesamtheiten zurückzuführen.
Daten mit diskreter Klassierung und
Stetig klassierte Daten
Daten mit diskreter Klassierung
Wenn die Daten in diskreter Klassierung vorliegen, können die Formeln für die metrischen Daten folgendermassen
angewandt werden.
Arithmetisches, harmonisches und geometrisches Mittel können auch einfach berechnet werden, wenn nur eine diskrete Klassierung der Daten mit J Ausprägungen (d.h. 8x1 , n1 <, 8x2 , n2 <, ... 8xJ , nJ <) vorliegt.
Arithmetisches Mittel:
êêx = ÅÅ1ÅÅ ⁄ J x n = ⁄ J x h
i=1 i i
i=1 i i
n
74
Skript Statistik und Stochastik
Harmonisches Mittel:
êêx = J ÅÅ1ÅÅ ‚ J x -1 n N
i
i
n
i=1
Geometrisches Mittel:
êêx = J‰ J x ni N n = ¤J x hi
i
i=1 i
i=1
-1
= J‚
J
i=1
xi -1 hi N
-1
ÅÅ1ÅÅ
Die verschiedenen Streumasse können auch berechnet werden, wenn nur eine diskrete Klassierung der Daten mit J
Ausprägungen (d.h. 8x1 , n1 <, 8x2 , n2 <, ... 8xJ , nJ <) vorliegt.
Varianz s 2 :
Ginis mittlere Differenz d:
Ginis mittlere Differenz D:
Spannweite R:
J
s2 = ÅÅÅÅ1n ⁄i=1
Hxi - êêx L2 ni = ÅÅ1nÅÅ ⁄ni=1 xi 2 ni - êêx 2 = ⁄ni=1 xi 2 hi - êêx 2
J
J
d = ÅÅ1nÅÅ ⁄i=1
†xi - xè 0.5 § ni = ⁄i=1
†xi - xè 0.5 § hi
1
J
J
J
D = ÅÅÅÅ
ÅÅ J
†x - xk § ni nk = ⁄i=1
†xi - xk § hi hk
⁄k=1
n2 ⁄i=1 ⁄k=1 i
R = Maximum@x j D-Minimum@x j D
8 j»n j >0<
8 j»n j >0<
Stetig klassierte Daten
Häufig liegen die Daten über ein metrisches Merkmal in stetiger Klassierung vor.
Stetige Klassierung bedeutet, dass die Werte des Merkmals in sogenannte Klassen zusammengefasst sind und an Stelle der
Einzeldaten lediglich diese Klassen und die Anzahl der Daten in jeder Klasse angegeben werden.
Insbesondere bei einem stetigen Merkmal macht es in der Regel keinen Sinn, die Häufigkeiten der einzelnen Werte zu
zählen (da ¶ viele verschiedene Werte vorkommen können und vermutlich jeder Wert in einer Datenreihe nur einmal
oder keinmal vorkommt).
Der Wertebereich der Daten wird deshalb in J nichtüberlappende Teilintervalle (Klassen) K j eingeteilt. Es gilt:
† Für die J Teilintervalle werden die J + 1 Grenzen 8g1 , g2 , ....gJ+1 < benötigt.
Die untere und obere Grenze können auch -¶ bzw. ¶ sein.
† Dies führt auf die J Teilintervalle K j =D g j , g j+1 D für j = 1, ... J . Das Intervall ist an der unteren Grenze offen und
an der oberen Grenze abgeschlossen. g j ist somit die untere Grenze und g j+1 die obere Grenze der Klasse j.
† Für jedes Teilintervall wird die Anzahl n j der Daten gezählt, die in jenes Teilintervall fallen, was dann auf die
folgende diskrete Klassierung führt: 8K1 , n1 <, 8K2 , n2 <, ... 8KJ , nJ <.
n
† Für jedes Teilintervall kann der Anteil h j = ÅÅÅÅnjÅÅ berechnet werden, was dann auf die folgende diskrete Klassierung
führt: 8K1 , h1 <, 8K2 , h2 <, ... 8KJ , hJ <.
Eine stetige Klassierung sagt nichts über die Verteilung der Daten innerhalb der einzelnen Klassen aus. Die stetige
Klassierung enthält deshalb weniger Informationen als die Urliste.
Deshalb wird man eine Urliste nur dann in Klassen einteilen, wenn dies notwendig ist. Mit den heute zur Verfügung
stehenden Mitteln der Datenverarbeitung stellt selbst bei grossen Datensätzen die Berechnung der statistischen Grössen kein Problem dar.
Es gibt jedoch Situationen, in denen stetig klassierte Daten angewendet werden (müssen):
† sei es, weil bereits bei der Erhebung der Daten eine Klassierung vorgenommen wurde.
Z.B. wenn nicht das exakte Einkommen erfragt wird, sondern nur ob das Einkommen in eines von mehreren
vorgegebenen Intervallen fällt;
† sei es dass zum Zwecke des Datenschutzes die Intervalle so gross gewählt werden, dass aus den Häufigkeiten der
stetigen Klassierung keine Rückschlüsse auf die Einzeldaten gezogen werden können;
75
Skript Statistik und Stochastik
† sei es weil nur wenige verschiedene Werte in der Urliste vorkommen;
Bei der Festlegung der Klassen sind einige Punkte zu beachten:
† Eine Faustregel besagt, dass für n Beobachtungen rund 10 Log10 HnL gleich grosse Klassen angemessen sind;
† Je nach Situation sind die Klassenbreiten unterschiedlich zu wählen;
† Wie sollen die untere und obere Grenze gesetzt werden, wenn die unterste und oberste Klasse unbeschränkt sind?
Wenn die Daten in stetiger Klassierung vorliegen, muss zu ihrer Auswertung die fehlende Information in geeigneter
Weise substituiert werden.
n
h
j
j
ÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
Der Quotient ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ wird als empirische Dichte der Daten in der Klasse K j bezeichnet.
nHg -g L
g -g
j+1
j
j+1
j
Sie ist umso grösser,
† je grösser die absolute oder relative Häufigkeit; und
† je kleiner die Klassenbreite ist.
Wenn man diese empirischen Dichten als waagrechte Linien über den Klassen (Intervallen) abträgt und an den Sprungstellen
senkrechte Hilfslinien einzeichnet, entsteht ein sogenanntes Histogramm.
Es gilt:
† Die einzelnen Rechteckflächen über den Klassen betragen Hg j+1 - g j L ÅÅÅÅÅÅÅÅ
ÅÅÅÅj ÅÅÅÅÅÅ = h j .
g j+1 -g j
h
† Die Fläche ist somit ein Mass für die relativen Häufigkeiten (Wahrscheinlichkeiten) und die relevante Grösse in
einem Histogramm.
J
† Die Gesamtfläche unter der empirischen Dichte beträgt somit gleich 1 (da ⁄i=1
h j = 1).
Im Gegensatz zur Betrachtung im vorherigen Abschnitt ("Diskrete Klassierung"), wo die statistischen Grössen exakt
berechnet werden konnten, können sie bei einer stetigen Klassierung nur approximativ berechnet werden.
Im Folgenden sollen einige Formeln angegeben werden, mit denen wir für eine stetige Klassierung die empirische
Verteilungsfunktion, Quantile, Lage- und Streuungsmasse wenigstens näherungsweise berechnen können.
Verteilungsfunktion
Im Abschnitt über die Ordinalskala haben wir die empirische Verteilungsfunktion definiert. Gemäss Definition kann
die Verteilungsfunktion an den Obergrenzen der Klassen K j exakt angegeben werden:
F@g j+1 D = ⁄i=1 hi ,
j
j = 1, 2, ... J
Ausserdem gilt:
F@xD = 0, für x  g1
F@xD = 1, für x > gJ+1
Innerhalb der Klassen wird dann linear interpoliert:
j
F@xD > F@g j D + ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ Hx - g j L,
Hg -g L
h
j+1
Quantile
j
für x œD g j , g j+1 ]
76
Skript Statistik und Stochastik
Wenn keine Klasse die Häufigkeit 0 hat, dann ist F@xD eine streng monoton steigende Funktion. Da sie ausserdem
stetig ist, kann zu jedem Wert p H0  p  1L die Gleichung F@xD = p eindeutig nach x (dem p-Quantil) aufgelöst
werden.
Wiederum kann mittels Interpolation die Lösung einfach gefunden werden.
p-F@g D
p-F@g D
j
x p > g j + ÅÅÅÅÅÅÅÅhÅÅÅÅÅÅÅÅÅÅÅÅ
Å Hg j+1 - g j L = g j + ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅjÅÅÅÅÅÅÅÅÅÅ Hg j+1 - g j L,
F@g D-F@g D
j
j+1
j
für p œD F@g j D, f @g j+1 D]
Arithmetischer Mittelwert
Wenn die Klassenmittelwerte êêx i exakt bekannt sind, kann auf die Formel für die diskrete Klassierung zurückgegriffen
werden.
J
J
êêx = ÅÅÅÅ1Å
êê
êê
‚x n =‚x h
n i=1 i i i=1 i i
Wenn die Klassenmittelwerte êêx i nicht bekannt sind, so ersetzt man sie durch einen geeigneten Wert, z.B. durch die
g j+1 +g j
Klassenmitte ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ .
2
Varianz
n
nj
êê - êêx L2 ÅÅÅÅ
Mit Hilfe des Varianzzerlegungssatzes s2 = ⁄Jj=1 s2j ÅÅÅÅnÅjÅ + ⁄Jj=1 Hx
ÅÅ kann man approximativ schreiben:
nÆ
´¨¨¨¨¨¨¨¨¨¨¨≠¨¨¨¨¨¨¨¨¨Æ ´¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨j¨¨≠¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨¨
s2int
nj
êê - êêxL2 ÅÅÅÅ
s2 º ⁄ Jj=1 Hx
ÅÅ
j
n
s2ext
falls s2j º 0 und falls die Klassenmittelwerte bekannt sind.
Wenn die einzelnen Klassen breit sind, kann diese Approximation einen grossen Fehler haben.
j+1
s2 º ‚ H ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅjÅÅ - êêx L ÅÅÅÅnÅjÅ
2
j=1
J
g
+g
2 n
falls s2j º 0 und falls die Klassenmittelwerte nicht bekannt sind.
Hier werden die Klassenmitten an Stelle der Klassenmittelwerte gebraucht.
Konzentrations- und Disparitätsmessung
Einer der erste Schritte bei der Analyse eines Marktes ist die Bestimmung der Marktkonzentration. Wenn der Markt
fragmentiert ist, stehen viele Unternehmen im Wettbewerb und die Wettbewerbstheorien und Fragen der Produktdifferentiation stehen im Vordergrund. Mit grösserer Konzentration und weniger Unternehmen, die am Markt teilnehmen,
werden oligopolistische Wettbewerbs- und Spieltheorien wichtiger. Schlussendlich ist bei nur einem Unternehmen die
Theorie der Monopole anwendbar.
In diesem Abschnitt werden wir einige Indizes und graphische Darstellungen kennen lernen, um die Marktkonzentration bzw. die Ungleichheit in Märkten kennenzulernen. Wir gehen (allgemein) von n Merkmalsträgern aus, die je ein
Merkmal xi H ¥ 0L - beispielsweise den Umsatz eines Unternehmens - haben und bei der die Merkmalssumme ⁄ni=1 xi
des ganzen Marktes eine sinnvolle Interpretation zulässt. Es soll dann untersucht werden, wie sich diese Summe auf
die einzelnen Merkmalsträger i verteilt.
Zwei Aspekte stehen bei diesen Untersuchungen im Vordergrund: die Disparität und die Konzentration.
Eine Disparität (oder Ungleichheit) liegt vor, wenn die Merkmalssumme ⁄ni=1 xi nicht gleichmässig auf die n Merkmalsträger
aufgeteilt ist.
77
Skript Statistik und Stochastik
Bei der Betrachtung der Disparität einer Verteilung von Merkmalswerten werden Anteile miteinander verglichen. Die
Anzahl der Merkmalsträger geht in die Betrachtung nicht ein. Ein klassisches Anwendungsgebiet der Disparitätsmessung ist die Messung der Einkommens- oder Vermögensdisparität in einem Land.
Wenn zusätzlich die Anzahl der Merkmalsträger, die sich die Merkmalssumme teilen, in die Betrachtungsweise mit
einbezogen wird, kann auch die Konzentration einer Verteilung untersucht werden.
Eine Konzentration liegt vor, wenn ein grosser Anteil der Merkmalssumme auf eine kleine Anzahl von Merkmalsträgern
entfällt.
Im Folgenden werden wir die hilfreichsten graphischen Darstellungen und Masszahlen zur Disparität und Konzentration besprechen.
Zur Illustration verwenden wir folgendes Beispiel: im untersuchten Markt betätigen sich 5 Unternehmungen mit den
folgenden Usätzen (in Millionen Euro): x = 8330, 120, 90, 30, 30<.
Man kann sich leicht ausrechnen, dass die Merkmalssumme ⁄ni=1 xi = 600 beträgt.
Konzentration
Bei der Konzentrationsmessung sorgt man dafür, dass die Daten absteigend sortiert sind: x1 ¥ x2 , ... ¥ xn .
xi
xi
Dann berechnet man die relativen Anteile: hi = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ = ÅÅÅÅ
ÅÅÅÅÅ . Da die xi absteigend sortiert sind, sind auch die hi
n êêx
⁄ni=1 xi
absteigend sortiert.
⁄i=1 i
Die Konzentrationsrate CR@ jD ist definiert als CR@0D = 0 und CR@ jD = ⁄i=1 hi = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ Å für j, 1, ... n und entspricht der Summe
⁄n x
j
j
x
i=1 i
der j grössten Merkmalsanteile.
Bei maximaler Konzentration (d.h. h1 = 1, alle anderen hi = 0) gilt: CR@ jD = 1 für j = 1, ... n.
Bei minimaler Konzentration (d.h. alle hi = 1 ê n) gilt: CR@ jD = ÅÅÅÅ1n für j = 1, ... n.
Beispielsweise bedeutet die "3 Firmen Konzentrationsrate" CR@3D = 0.80, dass die drei grössten Unternehmen einen
Marktanteil von 80 % haben.
Mit Hilfe der Konzentrationsrate lässt sich auch eine anschauliche graphische Darstellung konstruieren.
In einer Konzentrationskurve werden der Punkt 80, 0< sowie die n Punkte 8 j, ⁄i=1 hi = CR@ jD< mit absteigend sortierten hi
eingezeichnet: d.h. in der Abszisse steht der Index des Merkmalsträgers j und in der Ordinate der Anteil der j grössten
Merkmalsträger (d.h. die j-te Konzentrationsrate CR@ jD).
j
Konzentrationskurve
1
0.8
0.6
0.4
0.2
1
2
Für die Konzentrationskurve gilt:
3
4
5
78
Skript Statistik und Stochastik
† sie bildet das Intervall @0, nD in das Intervall @0, 1D ab, ist stückweise linear und wächst streng monoton vom Wert 0
bis zum Wert 1; die Steigungs des j-ten Segments ist h j ; da die Steigungen mit wachsendem j abnehmen ist die
Kurve konkav.
† der rechte obere ist (v.a. bei grossen n) weniger relevant. Oft berechnet man deshalb die Konzentrationsraten und
damit den Verlauf nur bis zu einer Anzahl m Hm  nL von Merkmalsträgern und vernachlässigt den Rest. Dann
müssen nur die m Anteile hi oder die m Werte xi sowie die Merkmalssumme angegeben werden.
† die Konzentrationskurve kann dazu benutzt werden, Konzentrationen auf verschiedenen Märkten zu vergleichen.
Wenn eine erste Konzentrationskurve I immer über einer zweiten Konzentrationskurve II verläuft (d.h.
CRI @iD > CRII @iD " i = 1, ... n), dann sagt man, dass der Markt I eine gleichmässig höhere Konzentration als
Markt II habe. Wenn zwei Märkte unterschiedliche n haben, dann müssen die fehlenden Konzentrationsraten des
Marktes mit dem kleineren n mit genügend CR@ jD = 1 ergänzt werden.
Um auch die Konzentrationen von Märkten miteinander vergleichen zu können, deren Konzentrationskurven sich
schneiden, benötigen wir weitere Kriterien. Im Folgenden besprechen wir zwei sogenannte Konzentrationsindizes, die
die Konzentration eines Marktes mit einer (einzigen) Zahl messen.
1
1
Der Rosenbluth Index KR ist ein Konzentrationsindex und berechnet sich nach der Formel KR = ÅÅÅÅ
ÅÅ Å = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ , wobei A
2A
H2 ⁄n i x L-1
der Teilfläche des Rechtecks @0, nD µ @0, 1D , die oberhalb der Konzentrationskurve liegt, entspricht.
i=1
i
Zur Herleitung dieser Formel kann man die Fläche über der Konzentrationskurve in Teilflächen Ai unterteilen, die
durch die Punkte 8i - 1, CR@i - 1D< und 8i, CR@iD< auf der Konzentrationskurve und die Punkte
80, CR@i - 1D< und 80, CR@iD< auf der Ordinate gegeben sind. Diese Teilflächen haben die Fläche
Ai = hi Hi - 1L + ÅÅÅÅ2i = hi Hi - ÅÅÅÅ12 L.
Die Summation dieser Flächen ergibt dann:
A = ⁄ni=1 Ai = ‚
n
i=1
hi Hi - ÅÅÅÅ12 L = ⁄ni=1 hi i - ÅÅÅÅ12 ⁄ni=1 hi = ⁄ni=1 hi i - ÅÅÅÅ12
Es gilt:
† bei minimaler Konzentration: KR = ÅÅÅÅ1n
† bei maximaler Konzentration: KR = 1
† allgemein: ÅÅÅÅ1n § KR § 1
Vielfach verwendet wird auch der folgende Konzentrationsindex.
Der Herfindahl Index KH ist ein Konzentrationsindex und berechnet sich nach der Formel KH = ⁄ni=1 h2i
Auch der Herfindahl Index lässt sich an der Konzentrationskurve veranschaulichen. Er entspricht der Summe der n
Quadrate, die durch jeweils zwei benachbarte Punkte der Folge 880, 0<, 8CR@1D, CR@1D<, ... 8n, CR@nD<< gegeben sind.
Es gilt (wie beim Rosenbluth Index):
† bei minimaler Konzentration: KH = ÅÅÅÅ1n ;
d.h. das Inverse des Herfindahl Index gibt die Anzahl der Merkmalsträger (z.B. Anzahl Unternehmen) an.
† bei maximaler Konzentration: KR = 1
† allgemein: ÅÅÅÅ1n § KH § 1
† 0 § KH  0.1 entspricht einem unkonzentrierten Markt;
† 0.10 § KH  0.18 entspricht entspricht moderater Konzentration;
† 0.18 § KH  1.00 entspricht entspricht hoher Konzentration;
79
Skript Statistik und Stochastik
Disparität
Im Gegensatz zur Konzentrationsmessung werden bei der Untersuchung der Disparität die Daten aufsteigend sortiert:
d.h. x1 § x2 , § ... § xn . Damit sind auch die daraus abgeleiteten relativen Häufigkeiten hi aufsteigend sortiert.
Eine anschauliche Darstellung der Disparität kann mit Hilfe der Lorenzkurve erreicht werden.
In einer Lorenzkurve werden der Punkt {0,0} und die n Punkte 8 ÅÅÅÅnj , ⁄i=1 hi U L@ ÅÅÅÅnj D< mit aufsteigend sortierten hi
eingezeichnet: d.h. in der Abszisse steht der Anteil ÅÅÅÅnj der j kleinsten Merkmalsträger an der Zahl der Merkmalsträgern und in
der Ordinate der Anteil dieser j kleinsten Merkmalsträger an der Merkmalssumme.
j
Bei maximaler Disparität (d.h. hn = 1, alle anderen hi = 0) gilt: L@ ÅÅnjÅÅ D = 0 für j = 1, ... n - 1 sowie L@ ÅÅÅÅnn D = 1
Bei minimaler Disparität (d.h. alle hi = 1 ê n) gilt: L@ ÅÅÅÅnj D = ÅÅÅÅnj für j = 1, ... n
Lorenzkurve
1
0.8
0.6
0.4
0.2
0.2
0.4
0.6
0.8
1
Für die Lorenzkurve gilt:
† in ihr werden zwei Anteile gegeneinander abgetragen;
† sie bildet das Intervall @0, 1D in das Intervall @0, 1D ab, ist stückweise linear und wächst monoton vom Wert 0 bis
i-1
ÅÅÅÅÅ , ÅÅÅÅni @ besitzt sie die Steigung n hi ; da die Anteile hi mit i anwachsen, gilt dies
zum Wert 1; in jedem Intervall @ ÅÅÅÅ
n
auch für die Steigung in jedem Intervall; die Lorenzkurve ist daher konvex.
† die Lorenzkurve kann dazu benutzt werden, Disparitäten auf verschiedenen Märkten zu vergleichen. Wenn eine
erste Lorenzkurve I immer über einer zweiten Lorenzkurve II verläuft, dann sagt man, dass der Markt I eine
gleichmässig geringere Disparität als Markt II habe.
Um auch die Disparitäten miteinander vergleichen zu können, deren Lorenzkurven sich schneiden, benötigen wir
weitere Kriterien. Im Folgenden besprechen wir zwei sogenannte Disparitätsindizes, die die Disparität mit einer
(einzigen) Zahl messen.
2 i-n-1
D
Der Gini-Koeffizient DG ist ein Disparitätsindex und berechnet sich gemäss DG = 2 H ÅÅÅÅ12 - BL = ⁄ni=1 hi ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
ÅÅÅÅÅÅ = ÅÅÅÅ
ÅÅ Å , wobei B
n
2 êêx
der Teilfläche des Rechtecks @0, 1D µ @0, 1D , die unterhalb der Lorenzkurve liegt, entspricht und D Ginis mittlere Differenz und
êêx das arithmetischen Mittel ist.
Die Herleitung verläuft analog zur Herleitung des Rosenbluth Index. Die Fläche unter der Lorenzkurve kann in
i-1
Teilflächen Bi unterteilt werden, die durch die Punkte 8 ÅÅÅÅ
ÅÅÅÅÅ , L@i - 1D< und 8 ÅÅÅÅni , L@iD< auf der Lorenzkurve und die Punkte
n
Hn-i+1L+Hn-iL
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
2 n-2 i+1
n
81, L@i - 1D< und 81, L@iD< gegeben sind. Diese Teilflächen haben die Fläche Bi = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ .
2
2n
Daraus folgt für DG (mit Hilfe von ⁄ni=1 hi = 1):
DG = 2 H ÅÅÅÅ12 - BL = 2 I ÅÅÅÅ12 - ‚
n
= ⁄ni=1 hi ÅÅÅÅnn - ‚
i=1
n
i=1
2 i-2 n+1
hi ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ M = 1 - ‚
2n
2 i-2 n+1
hi ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ = ‚
n
n
i=1
n
i=1
2 i-2 n+1
hi ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ
n
2 i-n-1
hi ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ
n
80
Skript Statistik und Stochastik
Es gilt:
† bei minimaler Disparität: DG = 0
† bei maximaler Konzentration: DG = 1 - ÅÅÅÅ1n
† allgemein: 0 § DG § 1 - ÅÅÅÅ1n
2 i-n-1
† DG lässt sich als (mit ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ ) gewichtetes Mittel der hi interpretieren, wobei die Gewichte sowohl positiv als auch
n
n
2 i-n-1
ÅÅÅÅÅÅÅÅÅÅ = 0 ist.
negativ sein können und die Summe ‚ ÅÅÅÅÅÅÅÅ
n
i=1
† Man kannn auch zeigen, dass der Gini-Koeffizient gleich der Hälfte des Quotienten aus Ginis mittlerer Differenz D
D
1
n
und dem arithmetischen Mittel êêx ist: DG = ÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅ
ÅÅÅÅ n
†x - x j §
2 êêx
2 êêx ⁄i=1 ⁄ j=1 i
Ein weiterer Disparitätskoeffizient, der besonders einfach ist und deshalb häufig verwendet wird, ist der Variationskoeffizient.
Der Variationskoeffizient v ist ein Disparitätsindex und berechnet sich gemäss v = ÅÅÅÅêêxsÅ , ist also der Quotient aus der
Standardabweichung s und dem arithmetischen Mittel êêx .
Es gilt:
† 0 § v =
è!!!!!!!!!!!!
n-1
† v = 0 ó x1 = x2 =. .. = xn (minimale Disparität)
è!!!!!!!!!!!!
† v = n - 1 ó x1 = x2 =. .. = xn-1 = 0, xn > 0 (maximale Disparität)
Zusammenhang zwischen Konzentrationsindizes und Disparitätkoeffizienten
Die in den vorausgegangenen Abschnitten diskutierten Konzentrationsmasse und Disparitätsindizes, wie auch die
entsprechenden Kurven sind eng miteinander verwandt.
Kurven
Das sieht man schon aus der Definition der Konzentrationskurve 9 j, ⁄i=1 hi = und der Lorenzkurve 9 ÅÅÅÅn , ⁄i=1 hi =. Es
muss jedoch berücksichtigt werden, dass die obigen hi unterschiedlich sortiert sind: im ersten Fall sind die relativen
Häufigkeiten hi absteigend und im zweiten Fall aufsteigend sortiert.
j
j
j
Trotzdem lassen sich diese zwei Kurven durch einfache geometrische Operationen ineinander überführen.
† Erster Schritt: Reskaliere die Abszisse der Konzentrationskurve; 9 j, ⁄i=1 hi = Ø 9 ÅÅÅÅn , ⁄i=1 hi =
Die Konzentrationskurve verläuft somit auch im Einheitsquadrat.
j
j
j
† Zweiter Schritt: Spiegele die Konzentrationskurve an der Diagonalen, die durch die Punkte 80, 0< und
{1,0}verläuft.
† Dritter Schritt: Spiegele die Konzentrationskurve an der Diagonalen, die durch die Punkte 81, 0< und {0,1}verläuft.
Zahlen
Ebenso einfach lassen sich Zahlen (d.h. die Konzentrationsindizes und die Disparitätskoeffizienten) ineinander transformieren. Es gelten:
1
1
1
KR = ÅÅÅÅ
ÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ
2A
2 nB
nH1-D L
KH =
v2 +1
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ
n
oder
2
v +1
Beweis von KH = ÅÅÅÅÅÅÅÅ
ÅÅ Å :
n
2
G
oder
v = n KH - 1
n KR -1
DG = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ
nK
R
81
Skript Statistik und Stochastik
ÅÅÅÅ1 ⁄n x 2
⁄n x 2
v +1
s +x
1
i=1 i
n
i=1 i
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅ1n I ÅÅÅÅÅÅÅÅ
J ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ Å = ‚
êêx 2ÅÅÅÅÅÅ M = ÅÅÅÅ
êêx 2 ÅÅÅÅÅÅ N = ÅÅÅÅÅÅÅÅ
n
n
H⁄n x L2
2
2
êê2
i=1 i
n
i=1
xi
ÅÅÅÅÅÅÅ M = ‚
I ÅÅÅÅÅÅÅÅ
⁄n xi
2
i=1
n
i=1
hi 2 = KH
Man sieht, dass mit steigender Zahl der Merkmalsträger n und bei gleichbleibender Konzentration (gemessen mit dem
Herfindahl-Index KH ) die Disparität (gemessen mit dem Variationskoeffizient v) linear mit n steigt.
Analoges gilt für den Rosenbluth-Konzentrationsindex und den Gini-Koeffizienten.
Gemeinsame Prinzipien
Den Konzentrations- und Disparitätsindizes sind die folgenden Prinzipien gemeinsam.
Prinzip der Anonymität: d.h. die Zuordnung der Merkmalswerte zu den Merkmalsträgern geht durch die Sortierung der
Urliste verloren.
Prinzip der Skaleninvarianz: d.h. die Einheit der Merkmalswerte spielt keine Rolle, da sich die Einheiten sowohl bei den
Indizes als auch bei den Kurven herauskürzen.
Prinzip des egalisierenden Transfers: d.h. falls ein Merkmalsträger mit höherem Merkmalswert einem anderen
Merkmalsträger mit geringerem Merkmalswert einen Merkmalsbetrag (der jedoch nicht so gross ist, dass sich die Rangierung
ändern würde) transferiert, dann reduzieren sich sowohl Disparität als auch Konzentration.
Unterschiede
Die Konzentrations- und Disparitätsindizes unterscheiden sich jedoch auch in zweierlei Hinsicht:
Nullergänzung: Wenn man dem Datenvektor x m Nullen hinzufügt, so verändert sich weder die Konzentrationskurve noch die
Werte der Konzentrationsindizes. Demgegenüber verlagert sich die Lorenzkurve nach unten und die Werte der
Disparitätsindizes werden grösser.
Replikation der Daten: Geht man von den Daten x1 , ... xn zu den Daten x1 , ... xn , x1 , ... xn über, d.h. dass man den Datensatz
um ein identisches Abbild erweitert, so verändern sich weder die Lorenzkurve noch die Werte der Disparitätsindizes.
Demgegenüber verschiebt sich die Konzentrationskurve nach unten, und die Werte der Konzentrationsmasse werden kleiner.
Rosenbluth- und Herfindahl-Index reduzieren sich bei einer m-fachen Replikation auf den m-ten Teil des Ausgangswertes.
Skript Statistik und Stochastik
82
9. Induktive Statistik
Einleitung
Nur mit einer Totalerhebung lässt sich eine vollständige Information über die Verteilung eines Merkmals X in einer
Grundgesamtheit gewinnen. Da dies selten möglich ist, versucht man mit Hilfe von Teilerhebungen Anhaltspunkte
über die unbekannte Verteilung zu gewinnen. Man spricht von Stichproben, wenn bei der Auswahl der Merkmalsträger
der Zufall eine wesentliche Rolle spielt.
Die induktive (zufallskritische, beurteilende) Statistik liefert auf Grund einer Stichprobe Aussagen über die Grundgesamtheit und hat zwei Aufgaben:
† Die Schätzung unbekannter Parameter der Grundgesamtheit mit Angabe der Vertrauensgrenzen (Schätzverfahren)
† Die Prüfung von Hypothesen über die Grundgesamtheit (Testverfahren)
Die deduktive Statistik (Wahrscheinlichkeitsrechnung) macht auf Grund eines Modells (über die Grundgesamtheit)
Aussagen über eine Stichprobe.
Es gibt verschiedene Arten von Tests.
† Signifikanztest testet, ob eine Hypothese verworfen werden muss oder nicht.
† Parametertest testet Hypothesen über einen Parameter.
† Anpassungstest prüft, ob eine beobachtete Verteilung mit einer hypothetischen verträglich ist.
Schritte beim Test von Hypothesen.
† Aufstellen der Nullhypothese.
† Aufstellen des Tests.
† Bei Gültigkeit der Nullhypothese ist ein bestimmter Ausgang sehr unwahrscheinlich.
† Risiko I oder Fehler I. Art (a), Risiko II oder Fehler 2. Art (b).
Ein statistischer Test ist ...
† Ein Verfahren, das für jede Stichprobe die Entscheidung, ob das Stichprobenergebnis die Hypothese stützt oder
nicht, herbeiführt, heisst statistischer Test.
† Die meisten statistischen Tests werden mit Hilfe einer Prüfgrösse (Teststatistik) durchgeführt. Eine solche Prüfgrösse ist eine Vorschrift, nach der aus einer gegebenen Stichprobe eine Zahl errechnet wird. Der Test besteht nun
darin, dass je nach dem Wert der Prüfgrösse entschieden wird.
83
Skript Statistik und Stochastik
Punktschätzungen
Punktschätzung für den Mittelwert
Der Mittelwert m des metrischen Merkmals X einer Grundgesamtheit sei unbekannt und soll mit Hilfe einer Zufallsstichprobe vom Umfang n geschätzt werden. Aus den beobachteten Merkmalswerten xi jedes einzelnen Stichprobenele`
⁄ni=1 xi
¯ = ments berechnet man das arithmetische Mittel x
n und erhält damit einen Schätzwert m.
Eine solche Schätzung heisst Punktschätzung, weil ein punktueller Wert als Schätzwert genannt wird und nicht etwa
ein Intervall. Es fehlt auch jede Angabe über die Zuverlässigkeit.
Um zu überprüfen, ob es sich bei dieser Formel um eine gute Schätzformel handelt (oder nicht), muss sie analysiert
werden. Der Schätzwert ist (wie man sich klarmachen kann) die Realisation einer Zufallsvariablen (die Merkmalsträger wurden ja zufällig aus der Grundgesamtheit ausgewählt), nämlich der durch n geteilten Summe der Xi .
In der Regel wird der Schätzwert
vom wahren Wert abweichen. Man kann jedoch einfach ausrechnen, dass der Erwarêê
tungswert der Schätzung m` mit dem Mittelwert der Grundgesamtheit m übereinstimmt. Dies wird erwartungstreue
Schätzung genannt. Das heisst auch, dass der Schätzfehler im Mittel verschwindet und nicht etwa eine systematische
Über- oder Unterschätzung vorliegt. Eine nicht erwartungstreue Schätzung heisst verzerrt, der Erwartungswert der
Abweichung Verzerrung (oder englisch Bias).
Die Berechnung der Varianz des Schätzwerts liefert (unter Berücksichtigung der Unabhängigkeit der Einzelstichσ2
proben) einen Wert von n , hat also die angenehme Eigenschaft, dass die Varianz mit zunehmendem Stichprobenumfang immer kleiner wird, was mit Konsistenz bezeichnet wird.
Punktschätzung für den Anteilswert
Im Gegensatz zum vorherigen Abschnitt, wo der Mittelwert einer metrischen Variable untersucht wurde, geht es beim
Anteilswert um eine ja/nein Entscheidung: hat der Merkmalsträger (das Individuum) eine bestimmte Eigenschaft oder
nicht, woraus sich dann der Anteil berechnen lässt.
Der in der Zufallstichprobe gefundene Anteilwert h ist eine Realisation der Zufallsvariablen, die als arithmetisches
Mittel von n Bernoulli-Variablen (ja/nein) definiert ist.
Ô
Ô
Der Schätzwert p gemäss der Schätzformel p = h ist erwartungstreu und konsistent.
Punktschätzung für die Varianz
Ô2
⁄i=1 Hxi −xL
Bei der Analyse der Punktschätzung für die Varianz stellt sich heraus, dass σ = s2 = n kein guter Schätzwn-1
ert ist. Er ist nicht erwartungstreu, er gibt einen um den Faktor ÅÅÅÅnÅÅÅÅÅÅ zu kleinen Wert an. Dies kann gezeigt werden,
n
indem man den Erwartungswert (von S 2 ) berechnt. Der Schätzwert für die Varianz muss also ÅÅÅÅ
ÅÅÅÅÅÅ s2 lauten. Den
n-1
Grund für diese Korrektur kann man darauf zurückführen, dass die Methode bereits einen Freiheitsgrad zur Berechnung des Mittelwerts verbraucht und die xi dann nicht mehr alle unabhängig sind, da ⁄ni=1 Hxi - êêx L = 0 gilt (d.h. die
Zentraleigenschaft des arithmetischen Mittels).
n
¯
2
84
Skript Statistik und Stochastik
Eigenschaften von Punktschätzungen
Wir haben gesehen, dass ein Schätzwert einer Punktschätzung eines Parameters eine Zufallsvariable ist und viele
Werte annehmen kann. Der Schätzwert wird von einer Schätzformel hervorgebracht und gründet sich auf einer Stichprobe. Man schätzt vielfach einen Parameter der Grundgesamtheit mit einem Parameter der Stichprobe. Nur bei der
Varianz musste eine Korrektur angebracht werden.
Eine Schätzformel (Schätzfunktion, Schätzer) hat eine Wahrscheinlichkeitsverteilung und aus ihr folgen gewisse
stochastische Eigenschaften. Zur Gütebeurteilung eines Schätzers q verwendet man einen Katalog von wünschenswerten Eigenschaften.
Ô
† Erwartungstreue, d.h. EJq N = q
Ô
† Asymptotische Erwartungstreue, d.h. limnض EJq N = q
† Konsistenz, d.h. die Varianz geht gegen 0
† Effizienz, d.h. die Varianz ist möglichst klein (im Vergleich zu anderen Schätzern)
Es kann sein, dass ein nicht erwartungstreuer Schätzer besser ist als ein erwartungstreuer, wenn seine Varianz kleiner
ist. Entscheidend ist die Nähe zum wahren Wert, was mit dem mittleren quadratischen Fehler bestimmt werden kann.
Intervallschätzungen
Einleitung
Keine Stichprobe kann völlig exakte Auskunft über die tatsächliche Verteilung oder auch nur die Masszahlen der
Verteilung von Merkmalen in einer Grundgesamtheit geben.
Bei den bisher behandelten Punktschätzungen wissen wir nicht, ob wir ihnen vertrauen können. Unter gewissen
Bedingungen ist es jedoch möglich, die Wahrscheinlichkeitsverteilung der Stichprobenwerte und damit den Schätzwerte wenigstens annähernd anzugeben. Mit Hilfe dieser Stichprobenverteilungen kann man dann das Vertrauen quantifizieren, also Wahrscheinlichkeiten angeben, mit denen man eine Schätzung für richtig hält.
Stichprobenverteilungen
Kenngrössen von Stichproben (z.B. Mittelwert, Anteilswert oder Varianz) sind Realisationen von Zufallsvariablen.
Ihre Wahrscheinlichkeitsverteilung nennt man Stichprobenverteilung.
Verteilung des Stichprobenmittelwerts
Wenn das metrische Merkmal X in einer Grundgesamtheit den Mittelwert m und die Varianz s2 hat, dann gilt für die
êêê
Verteilung des Stichprobenmittelwerts X .
êêê
† EHX L = m
s
† sêêê
ÅÅÅÅ!ÅÅ
è!!!!
X = ÅÅÅÅ
n
êêê
† X ist annähernd normalverteilt.
Diese Aussage folgt aus dem zentralen Grenzwertsatz (jedoch nur für unabhängige Ereignisse). Das heisst, dass die
Zufallsvariable, für die êêx = ÅÅÅÅ1n ⁄ni=1 xi eine Realisation darstellt, asymptotisch normalverteilt ist mit obigen Parametern.
85
Skript Statistik und Stochastik
Wie schnell die Verteilung konvergiert, hängt von der Ausgangsverteilung in der Grundgesamtheit ab. In den meisten
Fällen kann man davon ausgehen, dass bei einem Stichprobenumfang von n > 30 die Ausgangsverteilung kaum noch
eine Rolle spielt.
¯
êêê
X−µ
Wenn man obige Zufallsvariable X standardisiert (d.h. bildet) folgt daraus sofort die folgende Wahrscheinlichè!!!!
σê n
keitsaussage:
êêê
X -m
PI-z  ÅÅÅÅÅÅÅÅ
ÅÅ Å § zM = CDFHzL - CDFH-zL
sêêê
X
und noch leicht umgeformt:
êêê
êêê
PHm - z s êêê
X  X § m + z s X L = CDFHzL - CDFH-zL
Diese Beziehung wird direkter Schluss genannt. Man schliesst von der Grundgesamtheit auf die Stichprobe. Sie gibt die
Wahrscheinlichkeit an, mit der ein Stichprobenmittelwert in ein vorher bestimmtes Intervall fällt oder umgekehrt.
Beispiel
800 Personen besuchen eine Veranstaltung. Ihre durchschnittliche Körpergrösse beträgt 183 cm bei einer Standardabweichung von 10 cm. Es werden 25 zufällige Personen ausgewählt (mit "Zurücklegen").
êêê
† Mit welcher Wahrscheinlichkeit wird der Stichprobenmittelwert im Intervall 182 cm < X < 184 cm liegen?
† Wie gross ist das Intervall, in welches der Stichprobenmittelwert mit einer hohen Wahrscheinlichkeit von 0.9 fällt?
Lösung a
Es wird (mit n = 25) davon ausgegangen (zumal das Merkmal Körpergrösse schon weitgehend normalverteilt ist), dass
eine Normalverteilung vorliegt.
êêê
Wenn wir die Zahlen für m und s êêê
X in der linken Seite (m - z s X = 182) der Intervallformel einsetzen (die rechte liefert
10
Å
ÅÅÅ
Å
=
182
und
nach
z
augelöst z = ÅÅ12ÅÅ .
den gleichen Wert) erhalten wir 183 - z ÅÅÅÅÅÅÅÅ
è!!!!!!!!
25
Diesen z-Wert können wir nun in die CDF Verteilungsfunktion einsetzen und erhalten die Wahrscheinlichkeit.
CDFHNormalDistributionH0, 1L, 0.5L - CDFHNormalDistributionH0, 1L, -0.5L
0.38292492254802624`
Man könnte auch ansetzen (wegen der Symmetrie der Normalverteilung):
HCDFHNormalDistributionH0, 1L, 0.5L - 0.5L 2
0.38292492254802624`
Lösung b
Für 90% Wahrscheinlichkeit erhalten wir (wenn wir die 10% gleichmässig auf beide Seiten verteilen) die Wahrscheinlichkeiten von 5% und 95%. Daraus können wir die z-Werte berechnen.
z = Quantile@NormalDistributionH0, 1L, 0.95D = 1.6448
Ebenso ergibt
Quantile@NormalDistributionH0, 1L, 0.05D = -1.6450
Wir setzen dieses z in unsere Intervallformel ein und erhalten für das Intervall:
Skript Statistik und Stochastik
86
z 10
10 z
9183 - ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ!ÅÅÅ , ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ!Å + 183= = 8179.710, 186.290<
è!!!!!!
è!!!!!!
25
25
Intervallschätzung bei grossen Stichproben
Eine Stichprobe gilt dann als grosse Stichprobe, wenn die Abweichung der tatsächlichen Stichprobenverteilung von
der Normalverteilung vernachlässigt werden kann.
Die Intervallschätzung gründet auf der gleichen Wahrscheinlichkeitsaussage wie derjenigen im vorigen Abschnitt. Im
Argument der Wahrscheinlichkeitsfunktion P wird jedoch so umgestellt, dass man ein Intervall um m erhält.
Die Intervallschätzung ist die Umkehrung des direkten Schlusses und heisst deshalb auch Umkehrschluss oder Rückschluss.
Es wird von der Stichprobe auf die unbekannte Grundgesamtheit geschlossen.
Für grosse Stichproben gilt.
êêê
êêê
êêê
PHX - z s êêê
X  m § X + z s X L = CDFHzL - CDFH-zL = 1 - a
êêê
Wenn man auch noch X durch den Mittelwert êêx ersetzt erhält man das sogenannte Konfidenzintervall
êê - z sêêê , êêx + z s êêê D und schreibt:
@x
X
X
êê - z s êêê  m § êêx + z s êêê L = CDFHzL - CDFH-zL = 1 - a
PHx
X
X
† 1-a heisst die Konfidenzwahrscheinlichkeit und gibt an, wie sehr man darauf vertraut, dass der
feste aber unbekannte Wert m im Konfidenzintervall liegt.
† a heisst die Irrtumswahrscheinlichkeit
† In der Praxis muss zumeist eine Schätzung für die Varianz eingesetzt werden.
Intervallschätzung bei kleinen Stichproben
Sind die Stichproben zu klein, muss an Stelle der (nach dem zentralen Grenzsatz asymptotisch erreichten) Normalverteilung die tatsächliche Verteilung genommen werden.
Nur im Spezialfall, wenn das Merkmal in der Grundgesamtheit bereits (oder fast) normalverteilt ist, wird die Situation
wieder etwas einfacher, da dann auch die Stichprobe normalverteilt ist.
Wird die geschätzte Varianz eingesetzt muss (da in diesem Fall die Standardisierung eigentlich ein Quotient aus zwei
Zufallsvariablen ist), die Normalverteilung durch die Student-t Verteilung mit n - 1 Freiheitsgraden ersetzt werden und
wir erhalten
êê - t s êêê  m § êêx + t s êêê L = 1 - a
PHx
n-1 X
n-1 X
wo der t-Wert aus der Student-t Verteilung erhalten wird.
Beispiel
Eine Befragung unter einer Berufsgruppe mit 25 Absolventen hat ein durchschnittliches Einkommen von 42'720 CHF
bei einer Standardabweichung von 6'256 CHF ergeben. Wie gross ist das Einkommen für die ganze Grundgesamtheit
mit einer Irrtumswahrscheinlichkeit von 5%.
Lösung
Das Einkommen kann in guter Näherung als normalverteilt angenommen werden. Deshalb führt die kleine Stichprobe
auf die Student-t Verteilung (n - 1 ergibt 24; die 5% werden gleichmässig auf beide Seiten verteilt):
87
Skript Statistik und Stochastik
t = Quantile@StudentTDistributionH24L, 0.975D = 2.063898
` "#########
1
n #
Wir berechnen das geschätzte s` êêê
è!!!! Faktor) aus dem geschätzten s X (
X für den Mittelwert ( n−1 Faktor) für die
n
Grundgesamtheit:
n
"##########
ÅÅÅÅ
ÅÅÅÅÅÅ s
n-1
s = 6256; n = 25; s = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
è!!!!ÅÅÅÅÅÅÅÅÅÅÅÅ ;
n
n
n
"##########
ÅÅÅÅ
ÅÅÅÅÅÅ s "##########
ÅÅÅÅ
ÅÅÅÅÅÅ s
n-1
n-1
:42720 - t ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅ
Å
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
,
è!!!!
è!!!!ÅÅÅÅÅÅÅÅÅÅÅ t + 42720> = 840084, 45355<
n
n
Statistische Tests
Einleitung
Ein Verfahren, das für jede Stichprobe die Entscheidung, ob das Stichprobenergebnis die Hypothese stützt oder nicht,
herbeiführt, heisst statistischer Test.
† Die meisten statistischen Tests werden mit Hilfe einer Prüfgrösse (Teststatistik) durchgeführt. Eine solche Prüfgrösse ist eine Vorschrift, nach der aus einer gegebenen Stichprobe eine Zahl errechnet wird. Der Test besteht nun
darin, dass je nach dem Wert der Prüfgrösse entschieden wird.
è!!!!!
HX -m0 L n
† Prüfgrösse für den Einstichproben Gauss Test: Z = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ
s
êêê
† Theoretisch ist Z standardnormalverteilt.
Es ist oft nicht leicht zu entscheiden, wie lange Daten zur Überprüfung der Nullhypothese gesammelt werden sollen;
denn mit genügend grossen Stichprobenumfängen lassen sich fast alle Nullhypothesen ablehnen.
Schätzverfahren und Testverfahren sind Anwendungen der Stichprobentheorie. Bei den Testverfahren wird die mit der
Stichprobe gewonnene Information dazu verwendet, eine Entscheidung über eine Hypothese zu treffen. Es wird aber
nicht definitiv entschieden, ob die Hypothese richtig oder falsch ist, das heisst ob sie zutrifft oder nicht. Man wird als
Ergebnis eines statistischen Tests die gefasste Hypothese nur beibehalten oder verwerfen. Dabei kommt es darauf an,
dass die Wahrscheinlichkeit, eine richtige Hypothese zu verwerfen und eine falsche Hypothese beizubehalten, nicht
allzu gross ist.
Anfänglich wird eine Hypothese (Nullhypothese, Anfangshypothese) aufgestellt (über einen Parameter, die Verteilung
eines Merkmals etc.). Diese Hypothese kann richtig oder falsch sein. Sie wird jedoch nur geändert, wenn genügend
Beweise für das Gegenteil erbracht werden. Die Alternativhypothese (Gegenhypothese) könnte z.B. das logische
Komplement sein. Wichtig ist, dass sich die Nullhypothese und die Alternativhypothese gegenseitig ausschliessen.
Man unterscheidet zwischen einer einfachen oder Punkthypothese und einer zusammengesetzten. Die erstere spezifiziert einen singulären Parameterwert, die andere ein ganzes Intervall für den Wert des unbekannten Parameters.
Man unterscheidet auch zwei Fehlerarten:
† Fehler 1. Art: man verwirft die Nullhypothese, obwohl sie richtig ist;
† Fehler 2. Art: man verwirft die Nullhypothese nicht, obwohl die Alternative richtig ist.
Bei den Tests steht der Fehler 1. Art im Vordergrund. Dessen Wahrscheinlichkeit sollte möglichst klein sein, dabei
aber den Fehler 2. Art nicht zu gross werden zu lassen.
88
Skript Statistik und Stochastik
Testen von Hypothesen über Mittelwerte
Mit diesem Test wird eine Hypothese über den Mittelwert (z.B. Hypothese m = m0 ) getestet. Erst wenn der gefundene
Mittelwert êêx deutlich von diesem Wert abweicht (d.h. die Abweichung signifikant ist), wird man die Hypothese
verwerfen.
Mit der Verteilung des Stichprobenmittelwerts kann (bei Gültigkeit der Nullhypothese) für êêx ein Annahmebereich
êêê
und ein Verwerfungsbereich so bestimmt werden, dass die Wahrscheinlichkeit, mit der X in den Verwerfungsbereich
fällt, obwohl die Nullhypothese richtig ist, höchstens a beträgt. Die Wahrscheinlichkeit des Fehlers 1. Art a heisst
Signifikanzniveau.
ÅÅÅÅ0ÅÅÅÅ § z@1 - ÅÅÅÅa2Å D; H0 richtigM = 1 - a
PI ÅÅÅÅÅÅÅÅ
sêêê
êêêê
¦X-m ¦
X
Zweiseitige Fragestellung
Hier vergleicht man die absolute Abweichung zwischen dem in der
Stichprobe gefundenen Mittelwert und dem
»xêê-m0 »
Å
ÅÅÅ
Å
ÅÅ heisst Prüfgrösse. Die Nullhypothese ist zu
hypothetischen Wert mit seiner Standardabweichung. Der Quotient ÅÅÅÅÅÅÅÅ
sêêê
X
verwerfen, falls die Prüfgrösse den kritischen Wert z überschreitet. Der kritische Wert gibt gerade jene Stelle der
Verteilungsfunktion an, wo sie den Wert 1 - ÅÅÅÅa2Å hat. Er ist also das 1 - ÅÅÅÅa2Å Quantil.
Beispiel
In einem Restaurant sollen geeichte Biergläser im Ausschank 0.4 l Bier enthalten. Bei einer Stichprobe (Umfang 50)
ergibt sich eine durchschnittliche Füllmenge von 0.38 l bei einer Varianz von 0.0064 l2 . Kann man auf einem Signifikanzniveau von 5% die Nullhypothese aufrechterhalten, dass durchschnittlich 0.4 l Bier im Glas enthalten sind.
Lösung
Wir wollen ein bisschen ausholen. Die Stichprobe hat einen Mittelwert von 0.38 (den wir auch als Schätzer für die
Grundgesamtheit verwenden können) und eine Varianz von 0.0064. Dies ist jedoch die Varianz für die Stichprobe, die
Varianz für den Mittelwert ist n-mal kleiner. Wir wollen ausserdem die Varianz des Mittelwerts als Schätzer für die
n
Varianz der Grundgesamtheit verwenden, weshalb wir mit ÅÅÅÅ
ÅÅÅÅÅÅ multiplizieren müssen. Wir haben also m = 0.38 und
n-1
n
ÅÅÅÅ
Å
ÅÅÅ
Å
Å
0.0064
"####################
#
n-1
s êêê
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ mit n = 50.
X =
n
Mit nicht normierten Messwerten
50 0.0064
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ N.
Wir haben also die folgende Verteilung dist = NormalDistributionJ0.38, "##################
49 50
Wir plotten nun die CDF dieser (nicht normierten) Verteilung, wobei wir noch zusätzlich den Bereich markieren, der
im Wahrscheinlichkeitsintervall [0.025, 0.975] liegt.
1
0.8
0.6
0.4
0.2
0.35
0.4
0.45
0.5
89
Skript Statistik und Stochastik
Wir müssen uns nun fragen, ob der Prüfwert von 0.40 innerhalb dieses Bereichs liegt. Wir können der Graphik entnehmen, dass dies der Fall ist. Wir können jedoch auch unser Messintervall ausgeben lassen und sehen wiederum, dass
0.40 in diesem Intervall liegt:
8Quantile@dist, 0.025D, Quantile@dist, 0.975D< = 80.3576, 0.4024<
Der Wahrscheinlichkeitswert für den Prüfwert beträgt somit ...
cdfH0.40L = 0.95994
... ist also kleiner als 97.5% (aber nicht viel).
Mit normierten Messwerten
In der Regel arbeitet man jedoch mit normierten Verteilungen und Messwerten (siehe auch den theoretischen Teil
oben; die Verwendung der Standardnormalverteilung machte früher viel Sinn, denn dann musste nur diese eine
Verteilung tabelliert werden), d.h. wir nehmen die Standardnormalverteilung und zeichnen wieder das dem Wahrscheinlichkeitsintervall @0.025, 0.975D entsprechende Messintervall ein. Die Frage ist nun, ob die gemäss der Formel
»x -m0 »
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ normierte Prüfgrösse ...
sêêê
êê
X
†0.38 - 0.40§
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ = 1.7500
50 0.0064 #
"##################
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ
49 50
... innerhalb dieses Messintervalls liegt oder nicht.
Wir plotten deshalb die Normalverteilung mit den entsprechenden Messintervallen (2.5% und 97.5%) ...
1
0.8
0.6
0.4
0.2
-2
-1
1
2
... und sehen wiederum, dass die Prüfgrösse von 1.75 innerhalb des Intervalls liegt. Der Wahrscheinlichkeitswert der
Prüfgrösse ergibt wiederum den gleichen Wert von 95.99, ist also kleiner als 97.5%.
cdfH1.75L = 0.95994
Die Hypothese ist also (auf diesem Signifikanzniveau) nicht zu verwerfen.
Schritte
Nach der (zweimaligen) anschaulichen Herleitung soll noch eine Schritt für Schritt Anleitung zur Lösung dieser
Aufgabe gegeben werden:
† Aufstellen der zweiseitigen Hypothese: H0 : m = 0.4 l, H1 : m ∫ 0.4 l
† Schätzen der Standardabweichung gemäss der Formel s êêê
X =
n
50
ÅÅÅÅ
ÅÅÅÅÅÅ s2 #
ÅÅÅÅ
"##############
n-1
49ÅÅÅ 0.0064
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ Å = $%%%%%%%%%%%%%%%%%%%
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ = 0.0114286
n
50
»x -m0 »
†0.38-0.40§
† Berechnen der Prüfgrösse gemäss der Formel ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ ÅÅÅ = 1.75
sêêê
0.0114286
êê
X
† Bestimme den kritischen Wert zu a = 0.05: z = Quantile@NormalDistributionH0, 1L, 0.975D = 1.95996
Skript Statistik und Stochastik
† Testentscheidung: Die Prüfgrösse (1.75) ist kleiner als der kritische Wert (1.96), d.h. innerhalb des
Messintervalls. Deshalb kann die Hypothese beibehalten werden.
90
91
Skript Statistik und Stochastik
10. Zweidimensionale Verteilungen
Einleitung
Jede statistische Einheit einer Grundgesamtheit kann Träger einer Vielzahl von Merkmalen sein. Die univariate
Statistik beachtet nur ein Merkmal bzw. nur eine Variable, die multivariate Statistik beobachtet von jedem
Merkmalsträger mehrere Variablen.
Wir beschäftigen uns im Folgenden mit dem einfachsten Fall von zwei Variablen 8X , Y <. Das Ergebnis einer Messung
(Erhebung, Beobachtung) sind Wertepaare 8xi , yi <. Diese Wertepaare können in einem Streudiagramm eingetragen
werden.
Wenn nur endlich viele Ausprägungen der Merkmale X und Y vorkommen (endliche Verteilung), kann man auch eine
Kontingenz- bzw. Korrelationstabelle erzeugen, in der die Zeilen- und Spaltenköpfe durch X bzw. Y und die Tabelleninhalte
durch die (relative) Häufigkeit des Auftretens der entsprechenden Paare {xi , yi } gegeben sind.
Durch Bildung von Grössenklassen (statt Verwendung der diskreten Werte) lässt sich die Anzahl der Zeilen und
Spalten reduzieren. Es ist auch bei stetigen Verteilungen möglich, durch Bildung von Grössenklassen die Häufigkeiten
dieser Klassen in einer Kontingenztabelle darzustellen.
In diesem Kapitel beschäftigen wir uns auch mit Fragen der Korrelation, dem Grad der Beziehung zwischen diesen
Variablen. Dabei versuchen wir herauszufinden, wie gut eine lineare oder nichtlineare Gleichung die Beziehung
zwischen den Variablen beschreibt oder erklärt. Wenn alle Variablenwerte eine Gleichung vollkommen erfüllen,
bezeichnen wir diese Variable als vollständig korreliert oder sprechen von einer vollständigen Korrelation zwischen
ihnen. Sind nur zwei Variablen miteinander verknüpft, sprechen wir von einfacher Korrelation bzw. einfacher Regression, bei mehr als zwei Variablen von mehrfacher Korrelation bzw. mehrfacher Regression.
Positive bzw. direkte Korrelation heisst, dass Y im gleichen Sinne wächst wie X . Liegen alle Punkte in der Nähe einer
gekrümmten Kurve, wird die Korrelation nichtlinear genannt. Wenn keinerlei Beziehung zwischen den Variablen zu
erkennen ist, gibt es keine Korrelation zwischen den Variablen bzw. sind die Variablen unkorreliert.
Der folgende Plot zeigt drei Punktmengen mit negativ linearer Korrelation (rot), nichtlinearer Korrelation
(magenta) und keiner Korrelation (schwarz).
20
17.5
15
12.5
10
7.5
5
2.5
2
4
6
8
10
Qualitativ kann man bereits aus der Graphik entnehmen, wie gut eine Kurve eine Punktmenge beschreibt. Zur quantiativen Festlegung müssen jedoch Messgrössen für die Korrelation eingeführt werden.
In den folgenden Abschnitten diskutieren wir zunächst die Darstellungen und Möglichkeiten bei der Verwendung der
Kontingenztabelle.
92
Skript Statistik und Stochastik
Daran anschliessend diskutieren wir noch die Begriffe Kovarianz und Korrelationskoeffizient.
Kontingenztabelle
Einleitung
Wenn nur endlich viele Ausprägungen der Merkmale X und Y vorkommen (endliche Verteilung), kann man auch eine
Kontingenz- bzw. Korrelationstabelle erzeugen, in der die Reihen- und Spaltenköpfe durch xi bzw. yi und die
Tabelleninhalte durch die (relative) Häufigkeit des Auftretens der entsprechenden Paare {xi , yi } gegeben sind.
Wir wollen im Folgenden an Hand eines Beispiels die verschiedenen Begriffe erklären. Gegeben seien Messungen von
X und Y , bei denen X vier verschiedene Ausprägungen und Y fünf verschiedene Ausprägungen haben kann. Konkret
könnten folgende Messwerte resultieren:
x = 830, 40, 50, 60<;
y = 81, 2, 4, 5, 8<;
Wir führen nun Messungen durch und erhalten beispielsweise die folgende Häufigkeitstabelle:
ij
jj
jj x1
jj
jj x
jj 2
jj
jj x3
jj
j
k x4
y1
4
4
12
0
y2
8
8
10
4
y3
8
16
16
10
y4
0
20
28
16
y5 y
zz
0 zzzz
z
12 zzzz
zz
14 zzz
zz
10 {
Die Daten sind so zu interpretieren, dass 4 mal das Paar {x1 , y1 }, 8 mal das Paar {x1 , y2 } etc. gemessen wurde. Es
wurden insgesamt 200 Messungen durchgeführt:
Randverteilung
Die Ränder der Kontingenztabelle (bei denen die Reihen hiS bzw. die Spalten hSj aufsummiert sind, was durch das S
angedeutet wird) ermöglichen die Untersuchung nur des einen Merkmals, womit wir wieder bei der univariaten
Analyse gelandet wären. Diese eindimensionalen Verteilungen heissen Randverteilung der statistischen Variablen X
bzw. Y.
Randverteilung für die X
Zur Berechnung der Randverteilung für X (hiS ) müssen wir für jede Zeile über die Spalten summieren. Wir erhalten
nach Normierung durch die Anzahl der Messungen die gewünschte Randverteilung:
ij
jj
jj x1
jj
jj x
jj 2
jj
jj x3
jjj
k x4
y1
4
4
12
0
y2
8
8
10
4
y3
8
16
16
10
y4
0
20
28
16
y5
0
12
14
10
Xrv
0.1
0.3
0.4
0.2
yz
zz
zz
zz
zz
zz
zz
zz
zz
z
{
Diese Liste gibt die relativen Häufigkeiten an, ein X1 , X2 , ... zu messen: so wurde z.B. ein X1 in 10% der Fälle
gemessen.
Randverteilung für Y
Zur Berechnung der Randverteilung für Y (hSj ) müssen wir für jede Spalte über die Zeilen summieren. Die Berechnung ist analog zur Berechnung der Randverteilung für X.
93
Skript Statistik und Stochastik
ij
jj
jj x1
jj
jj x
jj 2
jj
jj x3
jjj
jj x
jj 4
j
k Yrv
y1
4
4
12
0
0.1
y2
8
8
10
4
0.15
y3
8
16
16
10
0.25
y4
0
20
28
16
0.32
y5
0
12
14
10
0.18
Xrv y
zz
0.1 zzzz
z
0.3 zzzz
zz
0.4 zzz
zz
0.2 zzzz
z
1.0 {
Die unterste Reihe dieser Tabelle gibt die relativen Häufigkeiten an, ein Y1 , Y2 , ... zu messen.
Darstellung der Randverteilungen und relativen Häufigkeiten
Wir wollen nun noch eine übersichtliche Darstellung der gemessenen Daten geben, bei der alle Daten normiert werden.
jij
jj
jj
jj
jj
jj
jj
jj
jj
jj
jj
j
k
x1
x2
x3
x4
Yrv
y1
0.02
0.02
0.06
0.00
0.10
y2
0.04
0.04
0.05
0.02
0.15
y3
0.04
0.08
0.08
0.05
0.25
y4
0.00
0.10
0.14
0.08
0.32
y5
0.00
0.06
0.07
0.05
0.18
Xrv
0.10
0.30
0.40
0.20
1.00
zyz
zz
zz
zz
zz
zz
zz
zz
zz
zz
zz
z
{
Wir können der Tabelle z.B. entnehmen:
† die Wahrscheinlichkeit das Wertepaar 8X2 , Y3 } zu messen ist 8%;
† die Wahrscheinlichkeit ein X2 zu messen ist 30% (Randverteilung ganz rechts);
Bedingte Wahrscheinlichkeiten
Im vorigen Abschnitt haben wir in der Tabelle die relativen Häufigkeiten sowie die Randverteilungen dargestellt.
Diese Werte können folgendermassen interpretiert werden:
† Die (gleichzeitige) Messung des Paares 8Xi , Y j < tritt mit der relativen Häufigkeit auf, die in der Tabelle an der
entsprechenden Position 8i, j< eingetragen ist.
† Die relative Häufigkeit des Wertes Xi (unabhängig davon was für Y gemessen wurde) ist durch das i-te Element
der Randverteilung für X gegeben (Spalte ganz rechts).
† Die relative Häufigkeit des Wertes Y j (unabhängig davon was für X gemessen wurde) ist durch das j-te Element
der Randverteilung für Y gegeben (letzte Zeile).
In diesem Abschnitt wollen wir uns mit den folgenden zwei Fragen beschäftigen:
† Wie gross ist die Wahrscheinlichkeit ein Xi zu messen, wenn ein bestimmtes Y j gemessen wurde?
† Wie gross ist die Wahrscheinlichkeit ein Y j zu messen, wenn ein bestimmtes Xi gemessen wurde?
Es interessiert also nun die Verteilung der relativen Häufigkeiten einer Variablen, wenn die andere auf einem bestimmten Wert festgehalten wird. Auf diese Weise erhält man einen wichtigen Einblick in die Art des Zusammenhangs
zwischen den beiden Werten. Diese sogenannten bedingten Verteilungen lassen sich leicht der Kontingenztabelle
entnehmen; man braucht nur die Zeilen oder Spalten der Tabelle durch den ihnen entsprechenden Wert der Randverteilung zu dividieren.
Bei unabhängigen statistischen Variablen sind die bedingten Verteilungen identisch und jeweils gleich der Randverteilung. Statistische Unabhängigkeit wird dabei so definiert, dass die gemeinsamen relativen Häufigkeiten gleich dem
Produkt der beiden dazugehörigen Randverteilungshäufigkeiten sind: hij = hiS hSj .
94
Skript Statistik und Stochastik
Wir fragen nun also nach bedingten Wahrscheinlichkeiten. Im Gegensatz zur obigen Normierung, wo mit der Anzahl
Messungen normiert wurde, müssen wir nun die Normierung mit den Werten der Randverteilung durchführen. Es resultieren
zwei Darstellungen (die bedingte Wahrscheinlichkeit für X bzw.Y).
Bedingte Wahrscheinlichkeit für X
Wir führen also die folgenden Schritte durch (zur Normierung jeder Spalte):
jij
jj x
jj 1
jj
jj x2
jj
jj
jjj x3
jj
jjj x4
j
k Norm
y1
0.200
0.200
0.600
0.000
1.000
y2
0.267
0.267
0.333
0.133
1.000
y3
0.160
0.320
0.320
0.200
1.000
y4
0.000
0.313
0.438
0.250
1.000
y5
zyz
0.000 zzzz
z
0.333 zzzz
zz
0.389 zzz
zz
0.278 zzzz
z
1.000 {
Diese Tabelle ist so zu interpretieren: wenn wir (z.B.) wissen, dass Y1 gemessen wurde, dann wurde auch X3 mit einer
Wahrscheinlichkeit von 60% gemessen.
Bedingte Wahrscheinlichkeit für Y
Die Berechnung der bedingten Wahrscheinlichkeit für Y erfolgt analog (es wird jede Zeile normiert).
ij
jj
jj x1
jj
jj x
jj 2
jj
jj x3
jj
j
k x4
y1
0.200
0.067
0.150
0.000
y2
0.400
0.133
0.125
0.100
y3
0.400
0.267
0.200
0.250
y4
0.000
0.333
0.350
0.400
y5
0.000
0.200
0.175
0.250
Norm
1.000
1.000
1.000
1.000
yz
zz
zz
zz
zz
zz
zz
zz
zz
z
{
Berechnung von Mittelwerten und Varianzen für X und Y
In diesem Abschnitt wollen wir uns mit der Berechnung der Mittelwerte und Varianzen beschäftigen.
Der Mittelwert für X berechnet sich mit der Formel êêx = ⁄ki=1 ⁄lj=1 hij xi (für Y analog).
Die Varianz für X berechnet sich mit der Formel s2X = ⁄ki=1 ⁄lj=1 hij Hxi - êêx L2 (für Y analog).
Man sieht, dass die Summe über j separat durchgeführt werden kann und deshalb die Randverteilungen zur Berechnung der Mittelwerte und Varianzen verwendet werden können:
† êê
x = ⁄ki=1 hiS xi und êêy = ⁄lj=1 hSj y j
l
† s2X = ⁄ki=1 hiS Hxi - êê
x L2 und s2Y = ‚
j=1
HhSj Hy j - êêyLL2
Kovarianz und Korrelationskoeffizient
Einleitung
Für die beiden Variablen X und Y bei bivariaten Daten gilt, dass der Mittelwert der Summe X + Y gleich der Summe
der Mittelwerte und der Mittelwert der Differenz X - Y gleich der Differenz der Mittelwerte ist.
Für die Varianz ist das Ergebnis nicht so einfach.
95
Skript Statistik und Stochastik
Eine Rechnung zeigt, dass
êêL
2 ⁄n Hx j -xêêL Hy j -y
j=1
s2X +Y = s2X + s2Y + ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ
n
und analog für die Differenz. Nur für den Spezialfall, dass der letzte Term verschwindet, wäre die Varianz einer
Summe gleich der Summe der Varianzen.
Dieser Term (ohne den Faktor 2) wird empirische Kovarianz oder kurz Kovarianz genannt und mit cXY bezeichnet.
Die Kovarianz ist nichts weiter als das arithmetische Mittel des Produkts der Abweichungen der einzelnen Beobachtungen von ihrem jeweiligen Mittel.
Wie für die Varianz gibt
esêêauch für die Kovarianz eine einfachere Berechnungsmöglichkeit:
êêL Hy -y
L
⁄nj=1 Hx j -x
⁄nj=1 x j y j
j
cXY = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ - êêx êêy = êêêê
x y - êêx êêy
n
n
Sind zwei Variablen X und Y statistisch unabhängig, ist die Kovarianz zwischen ihnen Null.
Man beachte jedoch, dass dieser Satz nicht umkehrbar ist: aus der statistischen Unabhängigkeit folgt zwar das Verschwinden der Kovarianz, jedoch liegt keineswegs immer Unabhängigkeit vor, wenn die Kovarianz verschwindet. In
der Tat misst die Kovarianz nur den linearen Anteil der statistischen Abhängigkeit.
An Stelle der Kovarianz wird vielfach der Korrelationskoeffinzient verwendet:
cXY
rXY = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ
s s
X Y
Eigenschaften des Korrelationskoeffizienten
† Normierung
Mit der Division durch die beiden Standardabweichungen (was natürlich nur erlaubt ist, wenn sie ungleich Null
sind) erhält man ein normiertes Mass für die Strenge des linearen statistischen Zusammenhangs. Der Korrelationskoeffizient hat das gleiche Vorzeichen wie die Kovarianz, liegt aber stets zwischen -1 und 1.
† Masstabsneutral
Wenn man eine der beiden Variablen linear transformiert (z.B. von Dollar in Euro umrechnet) bleibt der Korrelationskoeffizient unverändert.
† Vertauschung der Variablen
Wenn man die Variablen X und Y vertauscht, ändert sich der Korrelationskoeffizient nicht.
Beispiel 1
Für unser Beispiel des Abschnitts "Kontingenztabelle" erhalten wir für die Kovarianz und Korrelation.
Kovarianz:
4.5200
Korrelation:
0.2366
Der Wert von 0.236 für den Korrelationskoeffizienten deuet auf eine schwache positive Korrelation hin.
Es ist zu beachten, dass in der Definition der Kovarianz die Summe über alle Messungen genommen wird.
96
Skript Statistik und Stochastik
Beispiel 2
In der Einleitung zu diesem Kapitel haben wir Streudiagramme dargestellt. Nun wollen wir noch die Korrelationskoeffizienten für diese Tabellen berechnen. Wir erhalten:
-0.9935
rote Punkte
0.3603
-0.0120
lila Punkte
schwarze Punkte
20
15
10
5
2
4
6
8
10
Man sieht:
† Für die (approximativ) lineare Funktion resultiert ein Korrelationskoeffizient nahe bei -1.
† Für die (approximativ) quadratische Funktion resultiert ein positiver Korrelationskoeffizient von rund 0.4, obwohl
die x und y Werte über die quadratische Beziehung sehr stark miteinander korrelieren. Aber wie schon gesagt, die
Kovarianz bzw. der Korrelationskoeffizient misst nur die lineare Abhängigkeit.
† Für die Random Funktion resultiert ein Korrelationskoeffizient nahe bei 0 (d.h. unkorreliert).
Skript Statistik und Stochastik
97
11. Regression und Korrelation
Einleitung
In vielen Anwendungen der Statistik stellt sich die Aufgabe, eine Variable (z.B. Inflationsrate) durch eine oder mehrere andere Variablen (z.B. Geldmengenwachstum) zu erklären, indem ein in der Regel approximativer funktionaler
Zusammenhang zwischen den Variablen nachgewiesen wird.
Cross-sectional
Bei den Daten handelt es sich vielfach um Datenreihen, bei denen zur gleichen Zeit Beobachtungen 8xi , yi < von
(mindestens) zwei Eigenschaften für eine varierende dritte Eigenschaft 8i< aufgenommen wurden (cross-sectional).
Beispiel: 8i, xi , yi < = 8Land, Geldmengenwachstum, Inflationsrate<.
Beispiel: 8i, xi , yi < = 8Schüler, Körpergrösse, Gewicht<.
Zeitreihen
Alternativ kann es sich aber auch um Zeitreihen 8ti , yi < handeln, bei denen (mindestens) eine Ausprägung für verschiedene Zeitpunkte aufgenommen wurde.
Beispiel: 8ti , yi < = 8Jahr, Inflation<.
Funktionale Beziehung 8xi , f @xi D<
In beiden Fällen wird eine funktionale Beziehung 8xi , yi = f @xi D< bzw. 8ti , yi = f @ti D< zwischen einer unabhängigen
Variablen (xi oder ti ) und einer abhängigen Variablen (yi ) vorausgesetzt.
In beiden Fällen stellt sich also die Aufgabe, den Zusammenhang 8ti , f @ti D< bzw. 8xi , f @xi D< zu bestimmen.
Um solche Aufgaben zu lösen können qualitative (Scatterplots) oder die quantitativen (Korrelation, Regression)
Analysen angewandt werden.
Scatterplot
Ein Scatterplot liefert ein anschauliches Bild, wie die Datenpunkte zueinander in Beziehung stehen. Mit einem Blick
gewinnt man einen Eindruck, ob die Datenpunkte in einem linearen oder nichtlinearen oder gar keinem Zusammenhang stehen.
Um jedoch quantitative Aussagen über den funktionalen Zusammenhang zu machen, muss eine Korrelations- oder
Regressionsanalyse durchgeführt werden.
Korrelation
Bei der Korrelationsanalyse wird der Korrelationskoeffizient zwischen den beiden Datenreihen berechnet. Dies ist eine
Zahl zwischen -1 und +1 und ist ein Mass für den linearen Zusammenhang zwsichen den Datenpaaren 8xi, yi <.
Regression
Mehr Möglichkeiten zur Feststellung eines funktionalen (nicht nur linearen) Zusammenhangs bietet die Regressionsanalyse. Die Regressionsanalyse geht jedoch von weitergehenden Annahmen aus als die Korrelationsanalyse: z.B.
müssen die xi deterministisch sein und die Fehler der yi einer Normalverteilung folgen.
Wir werden uns in diesem Kapitel relativ ausführlich mit einer linearen Regression für eine einzige unabhängige
Variable xi beschäftigen und modellieren die Beziehung zwischen xi und yi durch ein lineares Modell:
98
Skript Statistik und Stochastik
`
`
yi = b0 + b1 xi + ei . Wir bestimmen die Gleichungen zur optimalen Schätzung der Param b0 und b0 sowie der Varianz
2
des Fehlerterms s`e` .
` `
2
Wir untersuchen auch im Detail die Zuverlässigkeit (bzw. den Fehler) dieser drei Parameter (b0 , b0 , s` ). Die Kenntnis dieser Fehler erlaubt es uns dann auch, Konfidenzintervalle und Hypothesentests für diese Parameter
durchzuführen.
Weiters definieren wir das sogenannte Bestimmtheitsmass R2 , das uns sagt, welcher Anteil der Streuung in yi mit der
Regression erklärt werden kann und welcher Teil durch die Fehlerterme ei gegeben ist.
Zum Abschluss verwenden wir die gefundene Regressionsgerade dazu, für ein gegebenes xn+1 den dazugehörigen Wert
yn+1 zu prognostizieren, und ein Fehlerband für das geschätzte y` n+1 anzugeben.
Scatter Plot
Ein Scatterplot ist eine graphische Darstellung, die die Beziehung zwischen Beobachtungen für zwei Datenreihen in zwei
Dimensionen darstellt. Die erste Beobachtung wird in der Abszisse, die zweite Beobachtung in der Ordinate dargestellt.
Mit einem Scatter Plot lassen sich die Daten-Paare anschaulich darstellen. Man sieht auf einen Blick den funktionalen
Zusammenhang. Ausserdem können Ausreisser gut erkannt werden.
Beispielsweise seien die folgenden Datenreihen (bzw. 8xi , yi < Paare) gegeben:
x
0.
2.
4.
6.
8.
10.
y 0.72 4.53 5.42 7.26 9.54 10.07
Dies ergibt den folgenden Scatter Plot:
10
8
6
4
2
2
4
6
8
10
Jede Beobachtung i im Scatterplot ist repräsentiert durch einen Punkt 8xi , yi < und die Punkte werden nicht verbunden.
Korrelation
Einleitung
Im Gegensatz zu einem Scatter Plot, der die Beziehung zwischen zwei Datenreihen 8xi , yi < anschaulich darstellt, drückt die
Korrelationsanalyse die Beziehung quantitativ mit einer einzigen Zahl, dem Korrelationskoeffizienten, aus.
99
Skript Statistik und Stochastik
Der sogenannte Korrelationskoeffizient ist ein Mass dafür, wie eng zwei Datenreihen 8xi , yi < miteinander in Beziehung
stehen; genauer ausgedrückt misst er die Richtung und das Ausmass des linearen Zusammenhangs zwischen zwei
Variablen.
Der Korrelationskoeffizient kann nur Werte aus dem Intervall @-1, 1D annehmen.
† Ein Korrelationskoeffizient > 0 drückt einen positiven linearen Zusammenhang zwischen den Datenreihen aus,
d.h. dass auch y zunimmt, wenn x zunimmt.
† Ein Korrelationskoeffizient  0 drückt einen negativen linearen Zusammenhang zwischen den Datenreihen aus,
d.h. dass y abnimmt, wenn x zunimmt.
† Ein Korrelationskoeffizient von 0 zeigt an, dass keine lineare Beziehung zwischen den zwei Variablen 8x, y<
besteht.
Ein grosser (absoluter) Wert des Korrelationskoeffizienten weist auf eine starke lineare Beziehung zwischen den zwei
Variablen hin.
Bei vielen Datenpunkten kann bereits ein kleiner Wert des Korrelationskoeffizienten auf eine lineare Beziehung
zwischen zwei Variablen hinweisen.
Berechnung des Korrelationskoeffizienten
Die Berechnung des Korrelationskoeffizienten kann am einfachsten mit Hilfe der Kovarianz angegeben werden.
Die Stichprobenkovarianz sx,y zwischen zwei Datenreihen x = 8xi < und y = 8yi < mit n Beobachtungen berechnet sich
zu:
n
¯L
Hxi − ¯
xL Hyi − y
;
sx,y = ‚ n−1
i=1
¯
mit den Mittelwerten ¯
x und y
⁄ni=1 xi
¯
x = n
;
⁄ni=1 yi
¯ = y
;
n
Die Stichprobenkovarianz ist somit der Durchschnitt des Produkts aus Hxi - êêx L und Hxi - êêx L, wobei diese Faktoren jeweils die
Abweichungen der entsprechenden Beobachtung von ihrem Stichprobenmitttelwert beschreiben.
Mit Hilfe der Standardabweichungen sx und s y der beiden Stichproben, die die Streuung der x- und y-Werte um ihren
Mittelwert beschreiben, und die folgendermassen definiert sind ...
¯L2
xL2
⁄ni=1 Hxi − ¯
⁄ni=1 Hyi − y
; sy = $%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
;
sx = $%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
n−1
n−1
... kann dann die Definition des Korrelationskoeffizienten r = rx,y kurz und prägnant geschrieben werden:
s
s
x,y
x,y
Der Korrelationskoeffizient rx,y = ÅÅÅÅÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅ ist die Kovarianz der beiden Variablen x und y, geteilt durch das Produkt
s s
"###################
x y
sx,x s y,y
der Stichprobenstandardabweichungen.
Der Korrelationskoeffizient hat die folgenden Eigenschaften.
† Wie die Kovarianz ist der Korrelationskoeffizient ein Mass für die lineare Beziehung zwischen
zwei Datenreihen.
100
Skript Statistik und Stochastik
† Im Gegensatz zur Kovarianz hat der Korrelationskoeffizient den Vorteil, dass er eine reine Zahl (ohne Einheiten)
und ausserdem auf das Interval @-1, 1D normiert ist. Er ist deshalb viel einfacher zu interpretieren.
† Die Normierungen Hn - 1L in der Definition der Kovarianz und den Standardabweichungen sx und s y heben sich
gerade auf und es folgt auch:
¯L
xL Hyi − y
⁄ni=1 Hxi − ¯
rx,y = ;
"###############################
¯L2#
xL2 "###############################
⁄ni=1 Hxi − ¯
⁄ni=1 Hyi − y
† Der Korrelationskoeffizient ist symmetrisch in x und y: rx,y = r y,x
† sx s y kann auch als "###############
sx,x s y,y# geschrieben werden.
x,x
† rx,x = 1, da rx,x = ÅÅÅÅ
Åx,xÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ = 1. Eine Datenreihe 8xi < hat perfekte Korrelation mit sich selbst.
è!!!!!!!!!!!!!!!!!!
sx sx
s s
s
s
x,x x,x
Berechnung
Wir sind nun in der Lage, den Korrelationskoeffizienten für unser Beispiel zu berechnen. Mathematica Definitionen:
x_i_ := xPiT; n = Length@xD;
⁄ni=1 xi êê ⁄ni=1 yi
êêx = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ; y = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ;
n
n
⁄ni=1 Hxi - êêx L2 %
⁄ni=1 Hyi - êêyL2
sx = $%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ ; s y = $%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ ;
n-1
n-1
n
Hxi - êêxL Hyi - êêyL
sx,y = ‚ ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ;
n-1
i=1
sx,y
rx,y = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅ ;
sx s y
Kovarianz = 12.724
Korrelationskoeffizient = 0.976286
Korrelationskoeffizienten können berechnet werden, wenn die Mittelwerte und Standardabweichungen sowie die Kovarianz
endlich und konstant sind.
Grenzen der Korrelationsanalyse
Der Korrelationskoeffizient misst den linearen Zusammenhang zwischen zwei Variablen. Der Korrelationskoeffizient
ist jedoch nicht immer zuverlässig. Dies kann verschiedene Ursachen haben:
Nichtlinearität
Beispielsweise können zwei Variablen eine starke nichtlineare Abhängigkeit - und trotzdem eine kleine lineare Korrelation - haben. Obwohl bei der Beziehung y = Hx - 4L2 die Daten vollständig korreliert sind, ergibt die Berechnung des
Korrelationskoeffizienten einen Wert von 0.
101
Skript Statistik und Stochastik
10
8
6
4
2
2
4
6
8
Korrelation = 0
Ausreisser
Der Korrelationskoeffizient kann auch unzuverlässig sein, wenn Ausreisser in einer oder beiden Datenreihen
vorhanden sind.
Ausreisser sind eine kleine Anzahl von Beobachtungen an beiden Enden (klein oder gross) einer Stichprobe.
Beispielsweise wird in der folgenden linearen Beziehung durch einen einzigen Ausreisser der Korrelationskoeffizient
von 1.00 auf 0.73 reduziert.
20
15
10
5
5
10
15
20
Korrelation = 0.969228
Wenn der Ausreisser eliminiert wird steigt der Korrelationskoeffizient wieder auf 1.00.
20
15
10
5
5
10
15
20
Korrelation = 1.
Die Berechnung des Korrelationskoeffizienten ist sehr empfindlich auf den Aufschluss von Ausreissern.
Ein Ausreisser darf nicht ohne Grund aus den Daten entfernt werden. Man muss sich zuerst versichern, ob der Ausreisser Information über die Beziehung zwischen den Datenpunkten enthält oder nicht.
Falls der Ausreisser keine Information enthält, und es sich um eine Fehlmessung bzw. Noise handelt, sollte er von der
Analyse ausgeschlossen werden.
Falls der Ausreisser jedoch Informationen enthält und auf eine relevante Beziehung zwischen den Datenpunkten
hinweist, darf er von der Datenanalyse nicht ausgeschlossen werden.
Skript Statistik und Stochastik
102
Ausserdem sollte generell untersucht werden, wie sich der Korrelationskoeffizient beim Auschluss von Ausreissern
ändert.
Wichtig ist auch zu berücksichtigen, dass eine Korrelation keine Ursache (kausale Verknüpfung) impliziert. Auch
wenn zwei Variablen stark korreliert sind, heisst dies nicht, dass ein bestimmter Wert einer Variable einen bestimmten
Wert der anderen Variablen verursacht.
Korrelationen können auch auf eine Beziehung hinweisen, die gar nicht existiert. Dies kann verschiedene Ursachen
haben:
† die Korrelation kann zufällig sein;
† die Korrelation wurde herbeigeführt durch eine Rechnung, die jede von zwei Variablen x und y mit einer dritten
Variable z vermischt; wenn beispielsweise zwei unkorrelierte Variablen durch eine dritte Variable dividiert werden.
† die Korrelation zwischen zwei Datenreihen entsteht dadurch, dass beide Datenreihen mit einer dritten Datenreihe
korreliert sind; wenn beispielsweise die beiden Korrelationen Alter/Grösse und Alter/Wortschatz auf die falsche
Korrelation Grösse/Wortschaft führen.
Signifikanz des Korrelationskoeffizienten
Es ist relativ einfach, den Korrelationskoeffizienten zwischen zwei Datenreihen 8xi < und 8yi < zu berechnen.
Wenn wir wissen, dass die linear Beziehung nicht auf Zufall beruht, können wir dann diese Beziehung für Voraussagen von y aus der Kenntnis (oder Voraussage) von x verwenden.
Um festzustellen, ob die berechnete Korrelation eine wirklich vorhandene Beziehung zwischen den Datenreihen
ausdrückt oder nur auf Zufall beruht, reicht die Grösse des Korrelationskoeffizienten allein nicht aus; es muss ein
Signifikanztest durchgeführt werden, um festzustellen ob der Korrelationskoeffizient der Population r wirklich von 0
verschieden ist.
Ein Signifikanztest verläuft analog zu den Hypothese Tests und enthält die folgenden Schritte:
† Aufstellen der Nullhypothese H0 , dass die Korrelation in der Population gleich 0 ist ( r = 0) und der Alternativhypothese (r ∫ 0), was auf einen zweiseitigen Test führt.
† Unter der Annahme, dass die beiden Variablen normalverteilt sind, führt dies auf die folgende Test Statistik
è!!!!!!!!!!!!
r n-2
t = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅ
è!!!!!!!!!!!!!
2
1-r
mit einer t-Verteilung und n - 2 Freiheitsgraden.
Wenn die Anzahl der Datenpunkte n erhöht wird, fällt der Wert des Korrelationskoeffizienten r, der notwendig ist, die
Nullhypothese (r = 0) zu verwerfen (d.h. t > tc ). Einerseits fällt tc (da die Anzahl der Freiheitsgrade n - 2 steigt) und
è!!!!!!!!!!!!
andererseits erhöht sich t (mit n - 2 ).
(Lineare) Regression
Einleitung
Als nächstes diskutieren wir ein weiteres Verfahren, die Beziehung zwischen zwei Datenreihen zu quantifizieren: die
Regressionsanalyse. Eine Regression erlaubt uns mit Hilfe einer Variablen x Voraussagen über eine zweite Variable y
zu machen, Hypothesen über die Beziehung zwischen den zwei Variablen zu testen und die Stärke der Beziehung zu
quantifizieren.
Zur Durchführung einer Regressionsanalyse modelliert man die Werte der "zu erklärenden" Variable y (abhängige
Variable, erklärte Variable, Regressand) als Funktion der Werte der anderen so genannten "erklärenden" Variablen x
103
Skript Statistik und Stochastik
(unabhängige Variable, Regressor) und eines Störterms e.
yi = f @xi D + ei = y@xi D + ei
Der Störterm beschreibt die als unsystematisch oder zufällig angesehenen Abweichungen vom exakten funktionalen
Zusammenhang. Die Funktion legt man bis auf gewisse Parameter vorweg fest und schätzt diese Parameter dann aus
den Daten. Die resultierende Kurve y@xD nennen wir die Regressionskurve für y aus x, da von x auf die y geschlossen
wird.
Der Rest dieses Abschnitts wird sich mit der Linearen Regression (auch Linear Least Square genannt) mit einer
einzigen unabhängigen Variablen x beschäftigen. Es wird also die lineare Beziehung der Form y = b0 + b1 x vorausgesetzt.
Modell Annahmen
Das Modell der linearen Regression (genauer lineare Einfachregression, da nur eine abhängige Variable x existiert)
führt auf den Ansatz
yi = b0 + b1 xi + ei
Diese Gleichung besagt, dass die abhängige Variable yi gleich dem Achsenabschnitt b0 plus der Steigung b1 mal der
abhängigen Variable xi plus einem Fehlerterm (Störterm, Residuum) ist. Der Fehlerterm ei repräsentiert denjenigen
Anteil der abhängigen Variablen, der nicht durch die abhängige Variable xi erklärt werden kann.
In diesem Modell wird weiters vorausgesetzt, dass ...
† ... die Werte x1 , x2 , ... deterministisch (d.h. fest gegeben) und nicht alle gleich (d.h. sx 2 > 0) sind; dies ist oft nicht
der Fall; wichtig ist vor allem, dass die unabhängige und abhängige Variable unkorreliert sind; dann kann den
Ergebnissen der Regression trotzdem vertraut werden;
† ... für die Verteilung der Fehlerterme (die nicht beobachtet werden können) folgendes gilt:
Erwartungswert@ei D = 0 " i
Varianz@ei D = s2 " i
Kovarianz@ei , e j D = 0 " i ∫ j
Das Modell besitzt drei Parameter: die beiden Regressionskoeffizienten b0 und b1 sowie die Residualvarianz s2 .
Dies sind Modellparameter (bzw. Parameter der Population) und sind nicht bekannt. Aus den Daten8xi , yi < können sie
jedoch geschätzt werden.
Mit der Methode der kleinsten Quadrate berechnet man die beiden (aus den Daten geschätzten) Regressionskoeffi`
`
zienten b0 und b0 , mit deren Hilfe man eine Gerade in den Scatterplot einzeichnen kann, die die beobachteten y-Werte
für die vorliegenden Werte von x am besten erklärt.
10
8
6
4
2
2
4
6
8
10
Fig. Scatterplot mit eingezeichneter Regressionsgerade.
Mit Hilfe dieser Regressionskoeffizienten können dann auch die geschätzten Fehler e`i und daraus die geschätzte
` 2 berechnet werden.
Residualvarianz s
Das genaue Vorgehen zur Berechnung dieser Parameter wird in den nächsten beiden Abschnitten gezeigt.
104
Skript Statistik und Stochastik
`
`
Berechnung der (geschätzten) Regressionskoeffizienten b0 und b1
Um die Parameter b0 und b1 zu bestimmen (bzw. zu schätzen), wird die Methode der kleinsten Quadrate angewandt.
Das heisst, dass die Summe der Fehlerquadrate minimiert wird:
⁄ni=1 ei 2 = ‚
n
i=1
Hyi - b0 - b1 xi L2
Um das Minimum zu finden, wird dieser Ausdruck nach b0 und b1 abgeleitet und gleich 0 gesetzt. Die daraus resultier`
`
`
enden Lösungen für b0 und b1 werden mit b0 und b1 sowie die dazugehörigen Fehler werden mit ei bezeichnet.
`
Die Ableitung nach b0 und Nullsetzen ergibt für b0 die Beziehung:
n
`
`
`
⁄ni=1 ei = ‚ Iyi - b0 - b1 xi M = 0
⁄ni=1
i=1
`
yi - ⁄ni=1 b0
-‚
n
i=1
`
b1 xi = 0
`
`
n êêy - n b0 - b1 n êêx = 0
`
`
b0 = êêy - b1 êêx
`
Analog folgt für b1 :
n
`
`
`
⁄ni=1 ei xi = ‚ Iyi - b0 - b1 xi M xi = 0
⁄ni=1
i=1
`
`
yi xi - b0 n êêx - b1 ⁄ni=1 xi xi = 0
` `
`
Wenn man nun die Gleichung für b0 (b0 = êêy - b1 êêx ) hier einsetzt folgt:
`
`
⁄ni=1 yi xi - Iêêy - b1 êêx M n êêx - b1 ⁄ni=1 xi xi = 0
êêL
`
sx y
⁄ni=1 yi xi -n êêy êêx
⁄ni=1 Hxi -xêêL Hyi -y
Covaricance@x,yD
b1 = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅ
ÅÅ Å
Variance@xD
sx 2
⁄n xi xi -n êêx êêx
⁄n Hx -xêêL2
i=1
i=1
i
Dabei wurde benutzt, dass ...
⁄ni=1 Hxi - êêx L Hyi - êêyL = ⁄ni=1 xi yi - êêy ⁄ni=1 xi - êêx ⁄ni=1 yi + n êêx êêy = ⁄ni=1 xi yi - n êêx êêy
... und analog dass ...
⁄ni=1 Hxi - êêx L2 = ⁄ni=1 xi xi - n êêx êêx .
Zusammenfassend gilt also
`
und
⁄ni=1 ei = 0
`
sx y
b1 = ÅÅÅÅ
ÅÅ ÅÅ
s 2
x
und
`
⁄ni=1 ei xi = 0
`
`
sx y êê
b0 = êêy - b1 êêx = êêy - ÅÅÅÅ
ÅÅÅÅÅ x
s 2
x
`
`
Die lineare Regression liefert somit die Parameter b0 und b1 , die die lineare Beziehung (Gerade) zwischen den Datenreihen beschreiben. Damit lassen sich ...
† ... für ein gegebenes xi das dazugehörige yi voraussagen;
`
`
† ... Hypothesen über die Parameter b0 und b1 testen; und
† ... die Stärke der Beziehung zwischen den beiden Variablen x und y quantifizieren.
Eigenschaften der Regressionsgerade
Die Regressionsgerade hat einige interessante Eigenschaften.
105
Skript Statistik und Stochastik
êê,y
êê} der Punktwolke, da gemäss
† Mittlere Gerade. Die Regressionsgerade läuft genau durch den Schwerpunkt {x
`
`
`
Definition von b0 gilt: êêy = b0 + b1 êêx
ˆ
sxy
sy
† Steigungsregression: es gilt b1 = s2x = rxy sx .
† das Vorzeichen der Steigung entspricht dem Vorzeichen des Korrelationskoeffizienten rxy ;
† die Steigung hängt vom Verhältnis der beiden Varianzen sx , sy ab;
† bei gegebenen Varianzen verläuft die Gerade um so flacher je schwächer der lineare statistische Zusammenhang zwischen den Variablen ist;
† Varianzminimierung. Die Varianz der Regressionsabweichungen wird minimiert.
Berechnung der Residualvarianz s2 (standard error of estimate)
Manchmal beschreibt die lineare Regression den Zusammenhang zwischen x und y recht gut, manchmal aber auch
nicht. Wir müssen in der Lage sein, zwischen diesen zwei Fällen zu unterscheiden, um die Regressionsanalyse auch
wirkunsvoll einsetzen zu können.
Ein Mass für die Güte der gefundenen Regressionsbeziehung ist die sogenannte Residualvarianz s2 , die mit Hilfe der Daten
folgendermassen geschätzt wird:
2
n
`
`
2
2
1
1
s` = ÅÅÅÅ
ÅÅÅÅÅÅ n e` = ÅÅÅÅ
ÅÅÅÅÅÅ
Iy - b0 - b1 xi M
n-2 ⁄i=1 i
n-2 ‚i=1 i
Die Wurzel aus diesem Ausdruck (d.h. s`) wird auch mit (geschätztem) Standardfehler der Regression sowie im
Englischen mit "standard error of estimate" (SEE) oder mit "standard error of the regression" bezeichnet.
Bei der Berechnung der Residualvarianz wird im Nenner der Faktor n - 2 verwendet, weil n Datenpunkte vorliegen
`
`
und das lineare Regressionsmodell zwei Parameter (die beiden Regressionskoeffizienten b0 und b1 ) abschätzt: der
Freiheitsgrad, d.h. die Differenz zwischen der Anzahl Beobachtungen und der Anzahl Parameter, ist demzufolge gleich
n - 2.
` 2 ist es nicht notwendig, die Fehlerterme zu berechnen. Es gilt:
Zur Berechnung von s
`2
s
n
2
`
`
1
= ÅÅÅÅ
ÅÅÅÅÅÅ
Iy - b0 - b1 xi M
n-2 ‚i=1 i
n
2
`
`
1
= ÅÅÅÅ
ÅÅÅÅÅÅ
Iyi - êêy + b1 êêx - b1 xi M
n-2 ‚
i=1
` 2
`
1
= ÅÅÅÅ
ÅÅÅÅÅÅ J⁄ni=1 Hyi - êêyL2 + b1 ⁄ni=1 Hxi - êêx L2 - 2 b1 ⁄ni=1 Hyi - êêyL Hxi - êêx LN
n-2
` 2
`
n
= ÅÅÅÅ
ÅÅÅÅÅÅ Js y 2 + b1 sx 2 - 2 b1 sx y N
n-2
` 2
n
= ÅÅÅÅ
ÅÅÅÅÅÅ Js y 2 - b1 sx 2 N
n-2
`
Im letzten Schritt wurde die Beziehung sx y = b1 sx 2 ausgenutzt. Es folgt also:
` 2
sx y 2
2
n
n
s` = ÅÅÅÅ
ÅÅÅÅÅÅ Js y 2 - b1 sx 2 N = ÅÅÅÅ
ÅÅÅÅÅÅ Js y 2 - ÅÅÅÅÅÅÅÅ
ÅÅÅÅ N
n-2
n-2
s 2
x
` `
` 2 nur von den fünf Grössen êêx , êêy, s , s und s abhängen.
Man sieht also, dass alle drei Parameter b0 , b1 und s
x
y
x,y
`
`
Berechnung der Varianzen für b0 und b1
`
Die Regressionskoeffizienten b0 und b1 (des Modells) können nicht exakt bestimmt werden; die geschätzten b0 und
`
b1 hängen von den vorliegenden Stichprobenwerten yi ab.
106
Skript Statistik und Stochastik
Wir können jedoch die Varianz dieser Koeffizienten bestimmen und so den möglichen Fehler abschätzen. Es gilt:
êêL
`
⁄ni=1 Hxi -xêêL Hyi -y
1
b1 = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅ
ÅÅÅÅ n Hx - êêx L yi
n sx 2 ⁄i=1 i
⁄n Hx -xêêL2
i=1
da
⁄ni=1 Hxi
i
- êêx L êêy = êêy ⁄ni=1 Hxi - êêx L = 0
Für die Varianz folgt:
1 2 n
V @b̀1 D = I ÅÅÅÅÅÅÅÅ
ÅÅÅÅ M ⁄i=1 Hxi - êêx L2 V @yi D
n sx 2
1 2 2 n
= I ÅÅÅÅÅÅÅÅ
ÅÅÅÅ M s ⁄i=1 Hxi - êêx L2
n sx 2
1
s
= I ÅÅÅÅÅÅÅÅ
ÅÅÅÅ M s2 n sx 2 = ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
n sx 2
n sx 2
2
2
Bei dieser Herleitung wurde benutzt, dass V @yi D = V @ei D = s2 gemäss Annahme.
Analog berechnet man V @b̀0 D, so dass zusammenfassend gilt:
Varianzen der Regressionskoeffizienten:
`
s2
s2
V@b1 D = ÅÅÅÅÅÅÅÅ
ÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
und
êêLÅÅ2ÅÅ
ns 2
⁄n Hx -x
x
i=1
i
`
` ⁄ni=1 xi 2
s2 ⁄ni=1 xi 2
V@b0 D = V@b1 D ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
ÅÅÅÅÅÅ = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ
êêLÅ2ÅÅÅÅ
n
n ⁄n Hx -x
i=1
i
Die Varianzen (Fehler) beider Schätzer hängen proportional von s2 und umgekehrt proportional von sx 2 ab.
Ist s2 gross, so streuen die Punkte stark um die Gerade. Ist s2 klein, liegen die Punkte nahe an der Gerade und die
Gerade kann genauer festgelegt werden.
Ist sx 2 klein, dann streuen die x-Werte kaum und nur ein kleiner Abschnitt auf der x-Achse dient zur Bestimmung der
Geraden. Für grosse sx 2 kann die Gerade deshalb genauer bestimmt werden. Für eine verlässliche Schätzung der
Steigung wird eine hinreichend grosse Streuung der erklärenden Variablen x benötigt. Ausserdem sollte die Gerade
nicht über den Bereich der gegebenen x-Werte hinaus extrapoliert werden.
Bestimmtheitsmass R2 (coefficient of determination)
Obwohl die Residualvarianz s2 uns einen Hinweis darauf gibt, wie zuverlässig wir ein bestimmtes y voraussagen können, sagt
sie uns trotzdem noch nicht, wie gut die unabhängige Variable die Variation in der abhängigen Variablen erklären kann.
Dies leistet uns jedoch das sogenannte Bestimmtheitsmass. Es misst den Anteil an der ganzen Variation in y, der durch die
Variation in x erklärt werden kann und kann auf zwei Arten berechnet werden:
Allgemeiner Fall:
s` 2
s` 2
y
y
y
e
R2 = ÅÅÅÅ
ÅÅÅÅÅ = 1 - ÅÅÅÅ
ÅÅ Å
s 2
s 2
Spezieller Fall (eine unabhängige Variable x):
R2 = rx y 2
Anschaulich
Diese Beziehung für das Bestimmtheitsmass (ein Mass, wie gut ein yi bei gegebenem xi vorausgesagt werden kann),
kann folgendermassen gefunden werden.
Wenn wir nicht wissen, wie die abhängige Variable y von der unabhängigen Variablen x abhängt, dann dient der
Mittelwert êêy als beste Voraussage. Ein Mass für die Güte der Voraussage besteht in diesem Fall in der (totalen)
1
Varianz von y, d.h. ÅÅÅÅ
ÅÅÅÅÅÅ n Hy - êêyL2 .
n-1 ⁄i=1 i
Wenn wir jedoch bereits mittels Regression einen Zusammenhang zwischen den xi und den yi gefunden haben, dann
`
`
können wir diese Beziehung dazu benutzen, das yi mittels y` i = b0 + b1 x genauer (als mit dem Mittelwert) vorauszusagen. Falls die Regressionsbeziehung y gut zu erklären vermag, dann sollte der resultierende Fehler kleiner sein als
n
2
2
mit dem Mittelwert. Wenn wir den Ausdruck ⁄ni=1 Hyi - êêyL2 als totale Variation und ‚ Hyi - y` i L = ⁄ni=1 e`i als
i=1
107
Skript Statistik und Stochastik
unerklärte Variation (die nach der Regression noch übrig bleibt) bezeichnen, dann können wir das Bestimmtheitsmass
R2 folgendermassen definieren:
‚
n
Hyi -y` i L2
s` 2
erklärte Variation
unerklärte Variation
i=1
e
R2 = ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = 1 - ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ = 1 - ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
ÅÅÅÅ
êêÅLÅÅÅ
2 ÅÅ = 1 - ÅÅÅÅ
totale Variation
totale Variation
sy 2
⁄n Hy -y
i=1
i
Ausführlicher
Im Folgenden soll diese Beziehung noch etwas genauer und ausführlicher hergeleitet werden.
`
In den vorangegangenen Abschnitten wurden aus vorliegenden Beobachtungen 8xi , yi < die Regressionskoeffizienten b0
`
und b1 berechnet bzw. geschätzt. Diese Koeffizienten können nun benutzt werden, um für eine unabhängige Variable
`
`
xi den Wert für die abhängige Variable yi zu schätzen bzw. zu prognostizieren nach der Formel y`i = b0 + b1 xi . Mit
dem Ansatz:
`
yi = y`i + ei
und der Mittelung folgt (da ⁄ni=1 e`i = 0):
êêy = êêy` + eề = êêy`
Für die Varianz gilt weiters:
sy2
n
êê 2
= ÅÅ1nÅÅ ⁄ni=1 Hyi - êêyL2 = ÅÅÅÅ1n ‚ Iy`i + e`i - y` M
i=1
n
n `
n
ề 2
êê` 2
êê
`
1
= ÅÅnÅÅ J‚ Iyi - yM + 2 ‚ ei Iy`i - y` M + ‚ Ièi - eM N
i=1
i=1
i=1
= s y` 2 + se` 2
ề
Zur Herleitung wurde beim dritten Term benutzt, dass e = 0 ist und deshalb eingefügt werden kann, sowie beim
zweiten Term, dass:
n ` `
n `
êê`
êê` n `
`
n ` `
‚i=1 ei Iyi - yM = ⁄i=1 ei yi - y ⁄i=1 ei = ‚i=1 ei Ib̀0 + b1 xi M - 0
`
`
= b0 ⁄ni=1 e`i + b1 ⁄ni=1 e`i xi = 0 + 0 = 0
Beim letzten Schritt wurde ⁄ni=1 ei xi = 0 benutzt; diese Beziehung war ein Resultat der Anwendung der Methode der
`
`
kleinsten Quadrate zur Bestimmung von b0 und b1 .
Die hergeleitete Beziehung bezeichnet man auch als Varianzzerlegungssatz:
s y 2 = s y` 2 + se` 2
Die Varianz der abhängigen Variablen y lässt sich demnach in zwei Teile aufspalten.
`
`
† s y` 2 ist die Varianz der exakt auf der Regressionsgeraden liegenden Werte y`i . Da die Definition von y`i = b0 + b1 xi
in die berechnete Regressionsgerade eingeht, nennt man s y` 2 auch den durch die Regression erklärten Teil der
Varianz s y 2 .
† s` 2 ist die Varianz der Residuen e` , die sogenannte Residualvarianz oder die durch die Regression nicht erklärte
e
i
Varianz.
Der obige Varianzzerlegungssatz ist auch die Basis für die Definition einer Masszahl zur Beurteilung der Güte oder
der Qualität einer berechneten Regressionsgeraden: das Bestimmtheitsmass. Es ist folgendermassen definiert:
s` 2
s` 2
y
y
y
e
Das Bestimmtheistsmass R2 = ÅÅÅÅ
ÅÅÅÅÅ = 1 - ÅÅÅÅ
ÅÅÅÅÅ ist der Anteil der durch die Regression erklärten Varianz an der Varianz der
s 2
s 2
y-Werte.
Es gilt:
108
Skript Statistik und Stochastik
† 0 § R2 § 1
`
† Es ist R2 = 1, wenn die Residualvarianz se` 2 = 0 ist; d.h. wenn alle empirischen Residuen ei = 0 sind; d.h. wenn alle
Punkte 8xi , yi < exakt auf der Regressionsgeraden liegen. In diesem Fall werden 100% der Varianz s y 2 der y-Werte
durch die Regression erklärt.
† Es ist R2 = 0, wenn die erklärte Varianz s ` 2 = 0 ist; d.h. wenn y` = y` =. .. = y` . Dann verläuft die Regressionsy
1
2
n
gerade parallel zur x-Achse; die Variation der y-Werte wird nicht durch die Variation der x-Werte erklärt.
Für die konkrete Berechnung des Bestimmtheitsmasses muss nicht auf die Berechnung von se` 2 zurückgegriffen
werden, da mit Hilfe von ...
n
n
2
`
`
2
= ÅÅ1nÅÅ ‚ Hy`i - êêyL = ÅÅÅÅ1n ‚ IIb̀0 + b1 xi M - Ib̀0 + b1 êêx MM
i=1
i=1
` 2
` 2
b1
= ÅÅÅÅ
ÅÅÅÅÅ n Hx - êêx L2 = b1 sx 2
n ⁄i=1 i
s y` 2
... für R2 folgt:
2
R =
s y` 2
ÅÅÅÅ
ÅÅÅÅ
sy2
=
` 2
b 1 sx 2
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ
sy 2
s
2
xy
= ÅÅÅÅÅÅÅÅsÅyÅÅÅÅÅÅÅ
ÅÅ M = rx y 2
2 ÅÅÅÅ = I ÅÅÅÅÅÅÅÅ
sx s y
xy
ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ s 2
22 x
sx
s
2
Das Bestimmtsheitsmass R2 ist also das Quadrat des Korrelationskoeffizienten rx y : R2 = rx y 2
Intervallschätzung und Tests
`
`
Nachdem wir die Parameter b0 und b1 bestimmt haben, interessiert uns natürlich die Frage, ob die Daten durch eine
Gerade gut approximiert werden, oder weiters wie gross die Zuverlässigkeit der gefundenen Parameter ist.
` `
2
Um Konfidenzintervalle für b0 , b1 oder s` konstruieren und Hypothesen über die Parameter testen zu können, nimmt
man zusätzlich an, dass die Residuen gemeinsam normalverteilt sind.
Ohne Herleitung seien die wichtigsten Ergebnisse angegeben:
Konfidenzintervall zum Niveau 1 - a:
`
`
b0 :
b0 ≤ s`b` tn-2,1-aê2
0
`
`
b :
b ≤ s` ` t
1
2
s` :
1
b1 n-2,1-aê2
`2
`2
Hn-2L s
Hn-2L s
A ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅ , ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅ E
c2 n-2, 1-aê2
c2 n-2, aê2
`
`
Hypothesen über b0 und b1 testet man mit den folgenden t-Tests:
Hypothesentests:
` `
`
b0 -b0,0
b0 :
T = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ ∂ tn-2
s`b
` `0
`
b1 -b1,0
b1 :
T = ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ ∂ tn-2
s`
b1
`
`
`
`
wobei getestet wird ob die geschätzten Werte b0 und b1 mit den Werten b0,0 bzw. b1,0 übereinstimmen.
Prognose
In den vorangehenden Abschnitten haben wir die Zuverlässigkeit der linearen Regression und den Fehler der Korrelationskoeffizienten und der Residualvarianz untersucht.
In der Praxis ist es häufig wünschenswert eine Regressionsanalyse dazu zu benutzen, um eine Prognose für eine
abhängige Variable zu machen, konkret um für ein gegebenes zusätzliches xi+1 das dazugehörige y` i+1 zu schätzen.
109
Skript Statistik und Stochastik
Wir wollen jedoch nicht nur diese Prognose machen, sondern auch den dabei auftretenden Fehler dieses Wertes
abschätzen können. Dies ist der Gegenstand dieses Abschnitts.
Nachdem wir für die Daten 8xi , yi < eine lineare Regression durchgeführt haben, können wir naheliegenderweise ansetzen:
`
`
`
`
Y i+1 = b0 + b1 xn+1 . Der Wert Y i+1 heisst Punktprognose.
Wir müssen berücksichtigen, dass wir bei der Benutzung des Regressionsmodells
Yi+1 = b0 + b1 xn+1 + en+1
`
`
und der geschätzten Parameter b0 und b1 , zwei Quellen von Fehlern haben. Wenn wir für den Prognosefehler ansetzen
...
`
`
`
Y i+1 - Yi+1 = b0 + b1 xn+1 - Hb0 + b1 xn+1 + en+1 L
... sehen wir, dass die erste Quelle der Fehlerterm (en+1 ) ist, dessen Fehler mit der Residualvarianz abgeschätzt werden
`
`
kann. Die zweite Quelle ist der Fehler bei der Bestimmung der geschätzten Regressionskoeffizienten b0 und b1 .
Wenn wir die wahren Werte der Regressionskoeffizienten wüssten, dann wäre die Varianz des Prognosefehlers gleich
der Residualvarianz s2 .
Eine genauere Untersuchung zeigt (ohne Herleitung):
Prognosefehler
Erwartungswert:
Varianz:
`
EAY i+1 - Yi+1 E = 0
êêL2
`
Hxn-1 -x
VAY i+1 - Yi+1 E = s2 I1 + ÅÅÅÅ1n + ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅ M
n s2
X
Die Varianz des Prognosefehlers ist offenbar dann am kleinsten, wenn xn-1 = êêx . Sie wächst quadratisch mit dem
Abstand zwischen xn+1 und êêx .
2
Wenn man für s2 die geschätzte Varianz s` einsetzt, erhält man die geschätzte Varianz für die Varianz des Prognosefe`
2
`
Hxn-1 -xêêL2
1
hlers: V AỲ i+1 - Yi+1 E = s I1 + ÅÅÅÅn + ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅ M
n s2
X
`
Y i+1 -Yi+1
Da die Grösse ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ eine Student-t Verteilung hat (mit n - 2 Freiheitsgraden) kann dies dazu benutzt werden, ein
`
V AỲ i+1 -Yi+1 E
`
`
Prognoseintervall zu bilden: Y i+1 ¡V AỲ i+1 - Yi+1 E tn-2,1- ÅÅa2ÅÅ
Unter der Normalverteilungsannahme an die Residuen überdeckt dieses Intervall die zukünftige Beobachtung Yn+1 mit
Wahrscheinlichkeit 1 - a.
`
`
Mathematica Lineare Regression - b0 und b1 Berechnungen
Beispiel mit Covariance und Mean
Für unser obiges Beispiel erhalten wir somit:
<< Statistics`MultiDescriptiveStatistics`
Covariance@X, YD
PrintA"b1 = ", b1 = E;
Covariance@X, XD
Print@"b0 = ", b0 = Mean@YD − b1 Mean@XDD;
b1 = 0.908857
b0 = 1.71238
Die folgende Graphik überlagert die Datenpunkte und die gefundene Regressionsgerade.
110
Skript Statistik und Stochastik
10
8
6
4
2
2
4
6
8
10
Mathematica kennt eine Reihe von eingebauten Funktionen, die auch zur Bestimmung der Regressionsgeraden verwendet werden können: FindFit, Fit, Regress etc.
Auf dies wird hier nicht weiter eingegangen.
Skript Statistik und Stochastik
111
12. Zeitreihen
Einleitung
In diesem Kapitel soll speziell auf Zeitreihen, d.h. Beobachtungen, die zu bestimmten Zeitpunkten in normalerweise
gleichen Zeitabständen aufgenommen wurden (z.B Jahresproduktion, Schlussnotierungen von Aktien an der Börse),
eingegangen werden.
Es ist allgemeine Konvention, die Zeit (an Stelle von x) mit t zu bezeichnen. Sie ist die unabhängige Variable in den
mathematischen Überlegungen.
Eine Zeitreihe kann anschaulich in einer Graphik (mit der Abszisse t) dargestellt werden. Die Erfahrung hat gezeigt,
dass es bestimmte charakteristische Bewegungen und Variationen gibt, die einzeln oder auch gemeinsam auftreten
können. Die Analyse und Separation der einzelnen Variationen ist vor allem auch im Hinblick auf Voraussagen für
zukünftige Entwicklungen von grosser Wichtigkeit. Diese Analyse nimmt in vielen Bereichen eine sehr wichtige
Stellung ein.
Die charakteristischen Variationen von Zeitreihen können in vier Haupttypen eingeteilt werden:
† Langfristige (säkulare) Variation (Bewegung, Trend)
Diese Variation beschreibt die allgemeine Richtung, in die sich der y-Wert über eine lange Zeitspanne bewegt.
Dies kann durch eine Trendlinie bzw. Trendkurve beschrieben werden.
† Zyklische Variation
Diese Variation beschreibt die langfristigen Schwankungen um die Trendlinie oder Trendkurve und werden auch
als Zyklen bezeichnet (Konjunkturzyklen).
† Saisonale Variation
Diese Variation beschreibt die identischen oder fast identischen Muster, denen eine Zeitreihe in den entsprechenden Monaten oder Quartalen von aufeinanderfolgenden Jahren unterworfen ist (z.B. Weihnachtsgeschäft).
Saisonal heisst zwar üblicherweise jährliche Regularität; man kann dieses Konzept jedoch auch auf Monate, Tage
oder Stunden erweitern.
† Zufällige (irreguläre) Variation
Diese Variation beschreibt sporadische, zufällige und in der Regel kurzzeitige Variationen. Die Ursachen können
jedoch auch langfristige Folgen haben.
Trendschätzung
Zur Schätzung des Trends (bzw. der mathematischen Beschreibung des Trends) bieten sich die folgenden Methoden
an:
† Methode der kleinsten Quadrate
Man wählt eine geeignete Trendkurve (Modell mit geeigneter Anzahl der Parameter) und findet mit der Methode
der kleinsten Quadrate die Parameter dieser Kurve.
† Freihand Methode
Man zeichnet von Hand den Trend in die Graphik ein. Diese Methode hat den Nachteil, dass die gefundene
Lösung vom persönlichen Urteil des Zeichnenden abhängt und nicht reproduzierbar ist.
† Methode des gleitenden Durchschnitts (siehe auch später)
Damit können zyklische, saisonale und irreguläre Muster (wenigsten zum Teil) beseitigt werden. Diese Methode
hat den Nachteil, dass Daten am Anfang und Ende einer Reihe verloren gehen. Sie kann auch Zyklen vortäuschen,
Skript Statistik und Stochastik
112
die in den Ausgangsdaten nicht vorhanden waren. Mit spezieller Gewichtung kann dieses Problem gemildert
werden.
† Methode der Semi-Mittelwerte
Man trennt die Daten in zwei (vorzugsweise gleich lange) Teile und bestimmt in beiden Teilen den Durchschnitt.
Mit diesen zwei Punkten wird dann eine Trendlinie gezogen. Dies funktioniert nur bei linearen oder fast linearen
Trends. Die Methode kann erweitert werden, indem man die Daten in mehr als zwei Teile teilt.
Saisonale Variation
Um den saisonalen Beitrag zur resultierenden Variation zu bestimmen, muss abgeschätzt werden wie die Daten der
Zeitreihe im Verlaufe eines durchschnittlichen Jahres von Monat zu Monat schwanken. Gesucht wird also der Saisonindex, bei dem für jeden Monat ein %Wert relativ zum Wert des gesamten Jahres (der gleich 1200% ist) steht.
Zur konkreten Berechnung bieten sich die folgenden Methoden an:
† Methode "Durchschnittliche Prozente"
Bei dieser Methode werden die Daten für jeden Monat als Prozentsatz für das ganze Jahr angegeben. Die
Monatswerte mehrerer Jahre werden dann gemittelt (arithmetischer Mittelwert, Median). Die erhaltenen Prozentsätze müssen eventuell noch auf 1200% für das ganze Jahr skaliert werden.
† Methode "Prozent Trend"
Bei dieser Methode werden die Daten für die einzelnen Monate als Prozentsätze der monatlichen Trendwerte
angegeben. Wiederum ergibt eine Mittelung über mehrere Jahre den erforderlichen Saisonindex.
† Methode "Prozent Gleitender Durchschnitt"
Wenn die monatlichen Ausgangsdaten durch die entsprechenden saisonalen Indexzahlen geteilt werden, spricht man
von Desaisonalisierung oder Anpassung auf Grund von saisonaler Variation. Solche Daten umfassen nach wie vor
Trend-, zyklische und irreguläre Variationen.
Zyklische Variation
Nach der Elimination des Trends und der saisonalen Schwankungen bleiben noch die zyklischen und irregulären
Schwankungen übrig. Wenn man die angepassten Daten (z.B.) über mehrere Monate mittelt, können auch noch die
irregulären Anteile eliminiert bzw. verkleinert werden, und man erhält die zyklische Variation.
Irreguläre Variaton
Nach den bisherigen Korrekturen bleiben noch die irregulären Variationen übrig. Sie sind in der Regel klein und
folgen einer Normal-Verteilung, d.h. dass kleine Abweichungen sehr häufig und grosse eher selten auftreten.
Achtung bei Extrapolationen
Die obigen Verfahrensschritte liefern eine mathematische Beschreibung der verschiedenen Variationen und können
ohne weiteres in die Zukunft extrapoliert werden. Es versteht sich von selbst, dass sich die Wirklichkeit nicht immer an
unsere Vorstellungen und Erwartungen hält und (in der Regel) auch nicht alle möglichen Einflüsse im mathematischen
Modell berücksichtigt werden (können).
113
Skript Statistik und Stochastik
Simulation
In dieser Simulation wird (exemplarisch) gezeigt, wie der Ansatz
DatenPunkt = Trend * Zyklisch * Saisonal * Irregulär
programmiert und simuliert werden kann. Da die einzelnen Anteile multiplikativ miteinander verknüft werden, werden
die Anteile als relative Abweichung von 1 (1 bedeutet keinen Einfluss) definiert.
Langfristige Variation (Trend) (blau): f1HxL = 0.05 x + 1
2px
Zyklische Variation (in der Regel jedoch nicht periodisch, grün): f2HxL = 0.2 sinH ÅÅÅÅÅÅÅÅ
ÅÅÅ L + 1
6
Saisonale Variation (periodisch, magenta): f3HxL = 0.1 sinH2 p xL + 1
Zufällige Variation (cyan): f4HxL = .05 Random@D + 1
Summe aller Variationen (rot): fAllHxL = f1HxL f2HxL f3HxL f4HxL;
Der Plot zeigt sehr schön die einzelnen Anteile.
Plot@8fAll@xD, f1@xD, f2@xD − 1, f3@xD − 1, f4@xD − 1<, 8x, 0, 10<,
PlotStyle → 8Red, Blue, Green, Magenta, Cyan<, PlotRange → AllD;
1.5
1
0.5
2
4
6
8
10
Es ist auch manchmal üblich für die Berechnung (an Stelle des Produkts) eine Summe zu verwenden. Dann sind die
einzelnen Bewegungen absolut und nicht als relativ (um 1 schwankend) einzugeben. Je nach vorliegender Aufgabenstellung ist die eine oder andere Wahl vorteilhaft.
Im Folgenden ginge es nun darum, die einzelnen Beiträge aus der beobachteten Variation herauszufiltern. Für die vier
Beiträge (der hier besprochenen Haupttypen) gibt es unterschiedliche Verfahren.
114
Skript Statistik und Stochastik
13. Stochastische Differentialgleichungen
Einleitung
Stochastische Differentialgleichungen (SDE) spielen nicht nur in der Physik (1905, Paper von Albert Einstein über die
Brown'sche Bewegung), sondern auch in der Finanzmathematik eine wichtige Rolle.
In diesem Kapitel soll exemplarisch die Preisentwicklung einer Aktie beschrieben werden.
Aktie
Die Preisentwicklung einer Aktie wird durch eine Stochastische Differentialgleichung beschrieben
„ y HtL = a y HtL „ t + s y HtL „ B HtL
yHt0 L = y0
Über die effektive Preisentwicklung können nur Wahrscheinlichkeitsaussagen gemacht werden.
Im Vergleich zu (praktisch) risikofreien Instrumenten wie Cash Accounts sind Investitionen in risikoreiche
Wertschriften wie z.B. Aktien mit grösseren Unsicherheiten behaftet.
Aktien haben einen Preis auf dem offenen Markt, der sich praktisch kontinuierlich ändert. Diese Fluktuationen des
Aktienpreises stellen die konstante Suche nach einem fairen Preis dar. Zusätzlich zu diesen (zufälligen) Fluktuationen
gibt es eine mehr oder weniger kontinuierliche (in der Zeit) Zunahme oder Abnahme des Werts, die auf das wirtschaftliche Umfeld oder firmenspezifische Faktoren zurückzuführen sind.
Stochastiche Differentialgleichung
Die Berechnung des Werts einer Aktie ist aus den angeführten Gründen nicht so einfach wie die Berechnung des Werts
von Cash. Die Änderung des Werts ist nicht nur von der Zeit und dem momentanten Wert der Aktie abhängig. In
komplizierter Art und Weise hängt die Änderung ausserdem von vielen weiteren Dingen ab (Inflationsrate, Zins,
Arbeitslosigkeit, Währungskurse, etc.), die nicht mit genügender Genauigkeit modelliert werden können.
Aus diesem Grund wird der Differenzialgleichung ein Zufallselement hinzugefügt, das diese nicht deterministischen
Terme enthalten soll. Dies führt auf den folgenden Ansatz für die zeitliche Änderung des Werts einer Aktie:
„ yHtL = aHt, yHtLL „ t + sHt, yHtLL „ BHtL
yHt0 L = y0
(1)
wo a(t,y(t)) „t den deterministischen Teil und s(t,y(t)) „B(t) den zufälligen Teil beschreibt. „ BHtL ist dabei das
sHt,yHtLL
"Differential" der Brownschen Bewegung BHtL, und sHt, yL eine gegebene Funktion ( ÅÅÅÅÅÅÅÅ
ÅÅÅÅÅÅÅÅÅÅ wird Volatilität genannt).
yHtL
Mit Brown'scher Bewegung ist gemeint, dass die „ BHtL's (unabhängige) normal verteilte Zufallsvariablen sind, mit
è!!!!!!!
Mittelwert 0 und Standard Abweichung „ t (Varianz „ t), i.e.,
è!!!!!!!
„ BHtL ~ NI0, „ t M.
Die obige Gleichung wird Stochastische Differenzialgleichung (SDE: stochastic differential equation) oder präziser
Stochastische Gewöhnliche Differenzialgleichung genannt.
Zusätzlich wird im obigen Gleichungssystem auch noch die Randbedingung - d.h. der anfängliche Wert der Aktie yHt0 L
- festgelegt.
115
Skript Statistik und Stochastik
Brown'sche Bewegung
Zuerst soll die Brown'sche Bewegung etwas Genauer untersucht werden. Dazu wird im Folgenden die Funktion
"BrownianMotion" definiert und verwendet:
Als Input verlangt sie die Startzeit (t0), die Endzeit (t1), den Anfangswert (y0) sowie die Anzahl der Schritte (K) der
Brown'schen Bewegung.
Bei der Berechnung, die auch auf das Statistik Paket zurückgreift, werden zuerst die Schrittweite (dt), dann die Liste
der einzelnen Schritte (dB, wobei Schritte aus einer Normalverteilung mit Varianz dt stammen) und schlussendlich mit
FoldList auch noch die Listen mit den Zeitpunkten und den aufsummierten Schritten (d.h. die Trajektorie) zu diesen
Zeitpunkten berechnet.
Diese drei Listen werden von der Funktion als Output retourniert.
Needs@"Statistics`NormalDistribution`"D;
t1 - t0
BrownianMotionHt0_, t1_, y0_, K_L := ModuleB8dt, dB<, dt = NB ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ F;
K
è!!!!!!
9dB = TableARandomANormalDistributionI0, dt ME, 8K<E, FoldList@8dt + #1P1T, #1P2T + #2< &, 80, 0<, dBD=F;
Im Folgenden werden vier solcher Trajektorien berechnet. Jeder Aufruf dieser Funktion gibt auf Grund des Aufrufs
von "Random" in der Funktion BrownianMotion eine andere Trajektorie. Mit "Interpolation" wird zum Plotten
zwischen den Punkten der Trajektorie linear interpoliert.
Plot@Evaluate@Table@Interpolation@BrownianMotionH0, 1, 0, 100LP2T, InterpolationOrder Ø 1D@sD, 84<DD,
8s, 0, 1<, PlotStyle Ø 8Red, Green, Blue, Black<, AxesLabel Ø 8"Zeit", ""<D;
2.5
2
1.5
1
0.5
-0.5
-1
0.2 0.4 0.6 0.8
1
Zeit
Monte-Carlo Lösung der SDE
Nachdem wir gesehen haben, wie die Brown'sche Bewegung programmiert werden kann, soll nun die SDE gelöst
werden. Lösen heisst hier, ein Verfahren zu finden, um den Verlauf des Aktienpreises (je nach Verlauf der
Brown'schen Bewegung) zu berechnen. Die SDE lautet in der diskretisierten Darstellung
yi+1 = yi + aHti , yi L „ t + sHti , yi L „ Bi
(2)
Zur Lösung der SDE wird die Funktion "SDESolver" verwendet. Im Vergleich zu "BrownianMotion" wird hier nicht
nur die Schrittlänge aufsummiert, sondern alle in der obigen Gleichung gegebenen Terme. Beim Aufruf der Funktion
muss auch die Drift aHt, yL und die nicht-deterministische Funktion sHt, yL eingegeben werden. Die Funktion "SDESolver" wird folgendermassen definiert:
Needs@"Statistics`NormalDistribution`"D;
SDESolverHaFunc_, sFunc_, t0_, t1_, y0_, K_L :=
t1 - t0
ModuleB8dt, G<, dt = NB ÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅÅ F; GH8t_, y_<, db_L := 8dt + t, y + dt aFuncHt, yL + db sFuncHt, yL<;
K
è!!!!!!
FoldListAG, 8t0, y0<, TableARandomANormalDistributionI0, dt ME, 8K<EEF;
Die einfachste SDE für eine Aktienpreis Entwicklung stellt die spezielle Wahl der Funktionen aHti , yi L = a yi und
sHti , yi L = s yi dar:
116
Skript Statistik und Stochastik
„ yHtL = a yHtL „ t + s yHtL „ BHtL
yHt0 L = y0
(3)
Experimentell (Monte-Carlo) kann diese Gleichung - mit Hilfe der oben definierten Funktion "SDESolver" - gelöst
werden. Im Folgenden werden a und s gesetzt sowie 10 mögliche Aktienpreisverläufe berechnet und geplottet.
aFuncHt_, y_L := .3 y;
sFuncHt_, y_L := .1 y;
t0 = 0; t1 = 2; y0 = 100; K = 1000;
Plot@Evaluate@Table@Interpolation@SDESolverHaFunc, sFunc, t0, t1, y0, KL, InterpolationOrder Ø 1D@tD, 810<DD,
8t, t0, t1<, PlotRange Ø 80, Automatic<,
PlotStyle Ø 8Red, Green, Blue, Magenta, Black, Cyan<, AxesLabel Ø 8"Zeit", "Aktienpreis"<D;
Aktienpreis
200
150
100
50
0.5
1
1.5
2
Zeit
Symbolische Lösung der SDE
Nach der numerischen Monte-Carlo Lösung soll noch auf die symbolische Lösung der SDE eingegangen werden.
„ yHtL = a yHtL „ t + s yHtL „ BHtL
yHt0 L = y0
(4)
Bei Stochastischen Differenzialgleichungen ist zu berücksichtigen, dass nicht die aus der Analysis gewohnten Regeln
(z.B. Kettenregel, Produktregel, Integration) zu verwenden sind, sondern die für Stochastische Gleichungen angepassten (z.B. Ito Kettenregel, Ito Integration). Auf diese Details wird hier jedoch nicht näher eingegangen.
Mit dem Ansatz für den zeitabhängigen Preis y(t)
z = logHyL
(5)
und Ausnutzung der Ito Kettenregel
H„ yL2 = s2 y2 „ t
(6)
1
1 -1
1
1
„ z = „ logHyL = ÅÅÅÅÅ „ y + ÅÅÅÅÅ ÅÅÅÅÅÅÅÅ2ÅÅ H„ yL2 = a „ t + s „ B - ÅÅÅÅÅÅÅÅÅÅÅÅÅ2Å s2 y2 „ t = Ja - ÅÅÅÅÅÅ s2 N „ t + s „ B
y
2 y
2y
2
(7)
kann man ableiten, dass
Es fällt auf, dass die Drift von z nicht gleich der Drift von y ist. Stochastische Integration liefert dann
s2 y
s2 y
i
i
zHtL = t jja - ÅÅÅÅÅÅÅÅÅÅ zz + s HBHtL - BH0LL + zH0L = t jja - ÅÅÅÅÅÅÅÅÅÅ zz + s BHtL + logHy0L.
2 {
2 {
k
k
(8)
yHtL = ‰zHtL = ‰Ia- ÅÅÅÅ2ÅÅ Å M t+s BHtL+logHy0L = y0 ‰Ia- ÅÅÅÅ2ÅÅ Å M t+s BHtL .
(9)
Exponenzieren liefert schliesslich
s2
s2
Diese Gleichung ist nicht besonders nützlich für die Berechnung von y(t), da die Brown'sche Bewegung B(t) nicht
gemessen werden kann und y(t) ja sowieso vom Markt geliefert wird.
Die Gleichung liefert jedoch Grenzen für den Verlauf des Preises. Man sieht auch schnell, dass der Median den
Verlauf y0 ‰Ia- ÅÅÅÅ2ÅÅÅÅ M t hat und etwas tiefer als der Durchschnittspreis (y0 ‰a t ) liegt.
s2
117
Skript Statistik und Stochastik
Im untenstehenden Plot werden einige (mögliche) Preisentwicklungen (grün), die gegebenen Grenzen (±s innerhalb
dessen 68.3% der Werte liegen sollten, ±2 s mit 95.5% und ±3 s mit 99.7%) in schwarz, der Median (blau) sowie der
Durchschnitt des Preises (rot) eingezeichnet.
y0 = 70; a = .5; s = .6; t0 = 0; t1 = 1; T = t1 - t0; K = 200;
aFuncHt_, y_L := a y;
sFuncHt_, y_L := s y;
s
Ja- ÅÅÅÅ
2ÅÅ ÅÅ N t+b s
2
ZHa_, s_, b_, t_L = y0 ‰
è!!!
t
;
Show@Plot@Evaluate@Table@Interpolation@SDESolverHaFunc, sFunc, t0, t1, y0, KL, InterpolationOrder Ø 1D@tD, 850<DD,
8t, t0, t1<, PlotRange Ø 80, 400<, PlotStyle Ø Green, DisplayFunction Ø IdentityD,
Plot@Evaluate@Table@ZHa, s, b, tL, 8b, -3, 3<DD, 8t, 0, T<,
PlotStyle Ø ReplacePart@Table@RGBColor@0, 0, 0D, 86<D, RGBColor@0, 0, 1D, 4D, DisplayFunction Ø IdentityD,
Plot@y0 ‰a t , 8t, 0, T<, PlotStyle Ø RGBColor@1, 0, 0D, DisplayFunction Ø IdentityD,
DisplayFunction Ø $DisplayFunction, AxesLabel Ø 8"Zeit", "Aktienpreis"<D;
Aktienpreis
400
350
300
250
200
150
100
50
0.2 0.4 0.6 0.8
1
Zeit
Mehrere Aktien
Die bisherige Untersuchung ging von einer einzelnen Aktie aus. In ähnlicher (jedoch etwas komplizierterer) Weise
können auch mehrere Aktien behandelt werden. Bei mehreren Aktien muss die Multinormal Verteilung verwendet
sowie die Kovarianz zwischen den Preisen berücksichtigt werden.