2 Addieren und Subtrahieren von Dezimalzahlen

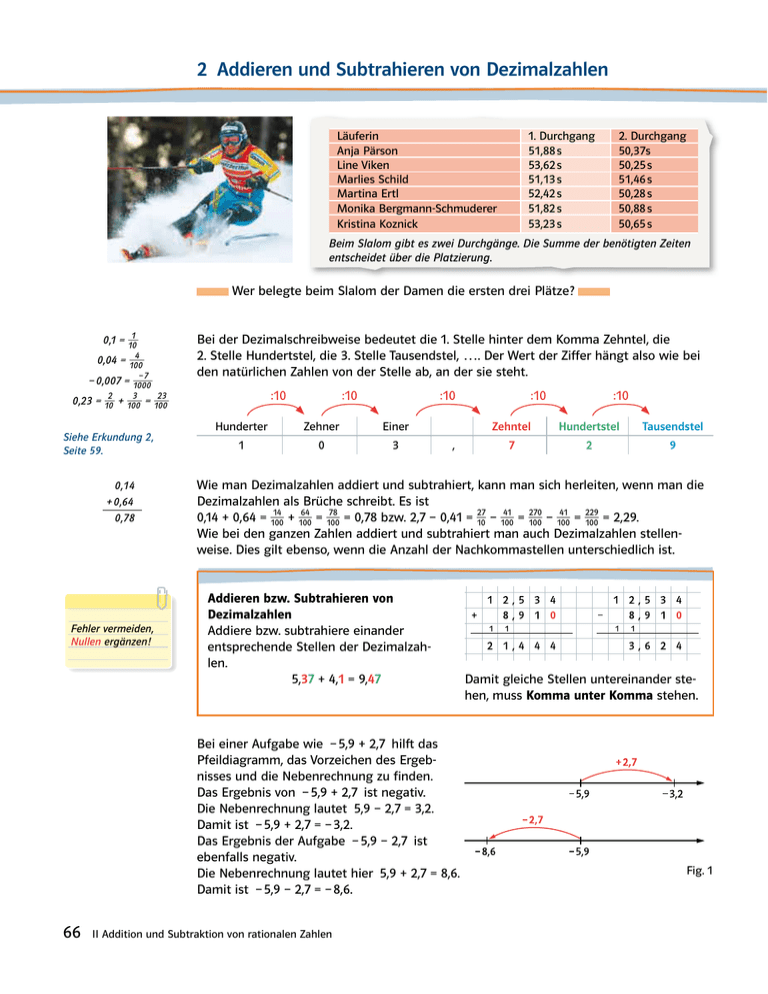
2 Addieren und Subtrahieren von Dezimalzahlen
Läuferin
Anja Pärson
Line Viken
Marlies Schild
Martina Ertl
Monika Bergmann-Schmuderer
Kristina Koznick
1. Durchgang
5Å,88 s
53,62 s
5Å,Å3 s
52,42 s
5Å,82 s
53,23 s
2. Durchgang
50,3ås
50,25 s
5Å,46 s
50,28 s
50,88 s
50,65 s
Beim Slalom gibt es zwei Durchgänge. Die Summe der benötigten Zeiten
entscheidet über die Platzierung.
Wer belegte beim Slalom der Damen die ersten drei Plätze?
1
0,1 = _
10  
4
0,04 = _
100  
–7
– 0,007 = _
1000  
3
23
2
_
_
0,23 = _
10  + 100  = 100  
Siehe Erkundung 2,
Seite 59.
0,Å4
+ 0,64
0,å8
Fehler vermeiden,
Nullen ergänzen!
Bei der Dezimalschreibweise bedeutet die 1. Stelle hinter dem Komma Zehntel, die
2. Stelle Hundertstel, die 3. Stelle Tausendstel, …. Der Wert der Ziffer hängt also wie bei
den natürlichen Zahlen von der Stelle ab, an der sie steht.
:10
:10
:10
Hunderter
Zehner
Einer
1
0
3
,
:10
Zehntel
Hundertstel
Tausendstel
7
2
9
Wie man Dezimalzahlen addiert und subtrahiert, kann man sich herleiten, wenn man die
Dezimalzahlen als Brüche schreibt. Es ist
229
64
78
270
14
27
41
41
_
_
_
_
_
_
_
0,14 + 0,64 = _
100  + 100  = 100  = 0,78 bzw. 2,7 – 0,41 = 10   – 100  = 100  – 100  = 100  = 2,29.
Wie bei den ganzen Zahlen addiert und subtrahiert man auch Dezimalzahlen stellenweise. Dies gilt ebenso, wenn die Anzahl der Nachkommastellen unterschiedlich ist.
Addieren bzw. Subtrahieren von
Dezimalzahlen
Addiere bzw. subtrahiere einander
entsprechende Stellen der Dezimalzahlen.
5,37 + 4,1 = 9,47
Bei einer Aufgabe wie – 5,9 + 2,7 hilft das
Pfeildiagramm, das Vorzeichen des Ergebnisses und die Nebenrechnung zu finden.
Das Ergebnis von – 5,9 + 2,7 ist negativ.
Die Nebenrechnung lautet 5,9 – 2,7 = 3,2.
Damit ist – 5,9 + 2,7 = – 3,2.
Das Ergebnis der Aufgabe – 5,9 – 2,7 ist
ebenfalls negativ.
Die Nebenrechnung lautet hier 5,9 + 2,7 = 8,6.
Damit ist – 5,9 – 2,7 = – 8,6.
66
:10
II Addition und Subtraktion von rationalen Zahlen
Damit gleiche Stellen untereinander stehen, muss Komma unter Komma stehen.
Fig. 1
Beispiel 1
Berechne. Bestimme zunächst das Vorzeichen des Ergebnisses.
a) 5,8 – 1,9
b) – 6,2 + 8,4
c) – 1,05 – 7,3
d) 17,3 – (– 18,5)
Mögliche Lösung:
a) 5,8 – 1,9 = 3,9
Vorzeichen positiv
b) – 6,2 + 8,4 = 2,2
Vorzeichen positiv; Nebenrechnung: 8,4 – 6,2 = 2,2
c) – 1,05 – 7,3 = – 8,35
Vorzeichen negativ; Nebenrechnung: 1,05 + 7,3 = 8,35
d) 17,3 – (– 18,5) = 17,3 + 18,5 = 35,8 Zuerst vereinfachen; Vorzeichen positiv.
Beispiel 2 Schriftliches Rechnen
Berechne schriftlich. Bestimme zunächst das Vorzeichen des Ergebnisses.
a) 7,89 – 5,63
b) 38,9 + 19,57
c) – 13,28 + (– 55,19)
d) 6,708 – 10,31
Lösung:
a) 7,89 Komma unter Komma schreiben;
b) 38,90 Komma unter Komma schreiben;
– 5,63 Vorzeichen positiv. + 19,57 eventuell „Endnull“ ergänzen;
2,26 58,47 Vorzeichen positiv.
c) Vorzeichen negativ.
Nebenrechnung:
13,28
+ 55,19
68,47
Also ist – 13,28 + (– 55,19) = – 68,47.
d) Vorzeichen negativ.
Nebenrechnung:
10,310
– 6,708
3,602
Also ist 6,708 – 10,31 = – 3,602.
Aufgaben
1 p Rechne im Kopf. Bestimme zunächst das Vorzeichen des Ergebnisses.
a) 1,4 + 0,6
b) 9,8 – 7
c) 1,9 + 2,3
0,8 + 2,1
2 – 1,3
1,9 – 2,3
3,7 + 1,7
– 4,2 – 2,4
– 1,9 – 2,3
Überlege eigene Aufgaben und stelle sie deinem Nachbarn.
d) – 0,5 + 1,7
12,3 – 15
– 25 – 13,3
Bei der Aufgabe 2
kannst du eine Ergebniskontrolle durch die
Quersummenprobe
machen.
2
Berechne schriftlich.
a) 5,22 + 2,73
b) 2,03 + 1,28
e) 3,45 – 1,89
f) 0,473 – 0,289
c) 4,27 + 16,2
g) 1 – 0,097
d) 0,021 + 5,23
h) 3,999 – 3,7
3
Bestimme das Vorzeichen und überschlage zuvor.
a) – 16,5 – 23,2
b) – 16,5 + 23,2
c) 16,5 + 23,2
e) – 1,2 + 25,2
f) 12,3 – 23,9
g) – 1,5 – 2,33
d) 16,5 – 23,2
h) 7 – 10,6
4
a) Um wie viel sind die Zahlen größer als 1? 1,5; 1,04; 1,33; 2,22; 1,001; 10,01
b) Wie viel fehlt noch bis 1? 0,5; 0,7; 0,36; – 1,5; – 0,15; – 10,5
c) Wie groß ist der Abstand zu 15 km? 9,7 km; 9270 m; 16,64 km; 17866 m
5
Übertrage in dein Heft und setze im Ergebnis das Komma an die richtige Stelle.
a) 4,4 + 0,8 = 52
b) 1,04 + 0,4 = 144
c) 2,55 – 7,6 = – 505
d) – 3,2 – 4,1 = – 73
6
Berechne jeweils die Summe und die Differenz der Zahlen.
a) 5,7; 3,6
b) – 1,8; 0,9
c) 99,9; 9,99
d) – 10,01; – 1,1
Fig. 1
II Addition und Subtraktion von rationalen Zahlen 67
7
Frau Hinz erledigte noch ein paar Ostereinkäufe. Ihr Einkaufsbon ist in Fig. 1
abgebildet.
a) Wie viel hat Frau Hinz für Süßigkeiten
und Osterdekor ausgegeben? Überschlage
erst und berechne anschließend genau.
b) Das Wildlachsfilet und die Margarine
hat Frau Hinz für ihre Nachbarin mitgebracht. Wie viel Geld bekommt sie von der
Nachbarin und wie viel hat ihr eigener Einkauf gekostet?
8
2,03
3
2
_
​   ​
1 ​ _25 ​
Ergänze in deinem Heft die magischen
Quadrate (Fig. 2 und Fig. 3). In jeder Zeile,
Spalte und jeder Diagonalen beträgt die
Summe 4,5.
9
Fig. 2
0,54
– 1,38
1,5
Fig. 3
a) Im Laufe eines Jahres beträgt die
Entfernung der Erde zur Sonne bei Sonnenferne 152,009 Mio. km und bei Sonnennähe 147,096 Mio. km. Wie groß ist der
Unterschied? Woher kommt er?
b) Der Erdumfang über die Pole gemessen
beträgt 40008,006 km und entlang des
Äquators 40075,161 km. Wie groß ist der
Unterschied? Woran liegt das?
Montag – Samstag
8 – 20 Uhr
EUR
Atlantik Wildlachsfilet 2.69 A
Atlantik Wildlachsfilet 2.69 A
Bunte Baiser Eier
0.79 A
Bunte Baiser Eier
0.79 A
Großes Ostersortiment
1.29 A
Großes Ostersortiment
1.29 A
Marzipan-Ei
0.59 A
Marzipan-Ei
0.59 A
Dekor-Marienkäfer
0.99 A
Dekor-Küken
0.99 A
4 x 0.48
H-Sahne 30 %
1.92 A
––––––
Summe
11 Pos. 14.62
Bockwurst 1 000 g
3.59 A
Pflanzen Margarine
1.19 A
Fleischsalat Joghurt
0.95 A
Metzgersalat
0.95 A
Metzgersalat
0.95 A
American Sandwich
0.72 A
––––––
Summe
17 Pos. 22.97 A
======
Geg
50.00
Rueck
27.03
A 7 %
1.50
22.97
*
*
*
*
VIELEN DANK FÜR IHREN EINKAUF
*
*
*
*
Frohe Ostern
Fig. 1
10 Hier wurde falsch gerechnet. Suche den Fehler und erkläre ihn. Gib anschließend das
richtige Ergebnis an.
Bist du sicher?
1 a)
Berechne im Kopf: 5,2 + 2,4
b)Berechne schriftlich: 6,59 + 13,8
c) Berechne:
15,8 kg + 6,3 kg
– 2,7 – 3,8
– 3,608 + 2,22
27,2 kg – 1100 g
2
a) Welche Zahl vermindert um 3,55 ergibt 7,99?
b) Welche Zahl muss man zu – 6,57 addieren, um 17,22 zu erhalten?
11 Welche Zahl musst du einsetzen, damit die Gleichung stimmt?
a) 6,4 + 4,8 = º
d) 12,45 – 8,05 = º
68 b) 7,2 + º = 9,6
e) 0,02 – º = 0,005
II Addition und Subtraktion von rationalen Zahlen
c) º + 10,5 = 15
f) º – 3,15 = 8,25
1,5 – 10,2
6,97 – 10,5
47,8 ​m3​ ​ – 800 ​dm​3​
12 º º, º – 0, º = ? Setze die Ziffern 4; 5; 6 und 7 so ein, dass das Ergebnis
a) möglichst groß wird,
b) möglichst klein wird,
c) genau 55,7 beträgt.
13 t Welche Zahlen (Fig. 1) ergeben die Summe 1? Verwende zwei, drei oder vier Summanden.
0,6
0,2
0,3715
0,5
0,0285
0,8
0,1715
0,3
0,6285
14 t Der Regierungsbezirk Köln hat eine Gesamtfläche von 7365 km2, davon werden
3527,77 km2
Fig. 1
19,31 km2
landwirtschaftlich genutzt.
bestehen aus Wald- und Grünland. Der
Rest sind Ödland, Wasserflächen, Verkehrs- und Siedlungsflächen. Wie viel km2 sind das?
15
Die Tabelle unten zeigt die Ergebnisse des olympischen Rodelwettbewerbs der Herren
2006 in Torino.
a) An wen gingen die Medaillen? Notiere die Reihenfolge nach dem gesamten Lauf.
b) Um wie viel Sekunden war der Sieger schneller als der Silbermedaillengewinner?
c) In welchem Durchgang war der Zeitabstand zwischen dem ersten und dem sechsten
am größten bzw. geringsten an?
Zeiten in s
Name
Land
Zöggeler
Italien
Demtschenko
Russland
Rubenis
Lettland
Benshoof
USA
Möller
Deutschland
Eichhorn
Deutschland
1. Durchgang
2. Durchgang
3. Durchgang
4. Durchgang
51,718
51,414
51,430
51,526
51,747
51,543
51,396
51,512
51,913
51,497
51,561
51,474
51,907
51,458
51,674
51,559
52,085
51,533
51,655
51,438
52,103
51,469
51,656
51,515
+
?
16
Übertrage Fig. 2 in dein Heft. Jedes Kästchen steht für eine der Ziffern 0, 2, 3, 6, 7, 9.
Jede Ziffer darf nur einmal vorkommen. Setze die Ziffern so ein, dass
a) der Wert der Summe möglichst klein ist, b) der Wert der Summe möglichst groß ist,
c) der Wert der Summe 9,45 beträgt,
d) der Wert der Differenz möglichst klein ist,
e) der Wert der Differenz 6,12 beträgt.
f) Erkläre, warum es bei den Aufgaben mit Summen immer mehrere Möglichkeiten gibt.
Kistenmaße (Länge × Breite × Höhe)
17 p Karl Schmidt soll mit seinem Kleintransporter verschiedene Kisten zu einem
1,76 × 0,65 × 1,14 m
1,51 × 0,29 × 0,75 m
Kunden fahren. Die Maße für die Lade1,76 × 0,92 × 1,14 m
1,49 × 1,38 × 0,75 m
fläche betragen 3,30 × 1,70 × 1,70 m. Die
0,76 × 1,65 × 0,51 m
1,48 × 0,68 × 0,89 m
Maße der acht Kisten stehen in der neben0,98 × 1,65 × 0,51 m
1,48 × 1,00 × 0,89 m
stehenden Tabelle.
Überlege dir mit deinem Nachbarn eine Empfehlung für Herrn Schmidt, wie er seinen
Transporter beladen sollte. Vergleicht eure Empfehlung mit der einer anderen Gruppe.
,
,
–
,
,
?
Fig. 2
Das ist leider nicht
erlaubt!
18
Berechne. Überlege dir jeweils eine passende Sachsituation und schreibe sie auf.
a) 610 m + 0,45 km – 0,05 km
b) 3,2m3 + 255 ø – 3300dm3
19
a) Forme bei 0,35 + 1,25 beide Summanden als Brüche um und addiere sie.
3
24
_
b) Forme bei _
100  + 10   beide Summanden als Dezimalzahlen um und addiere sie.
c) Begründe allgemein mithilfe der Regeln für Brüche, dass man Dezimalzahlen stellenweise addieren kann.
II Addition und Subtraktion von rationalen Zahlen
69