Aufgaben zum Stirlingschen Kreisprozess

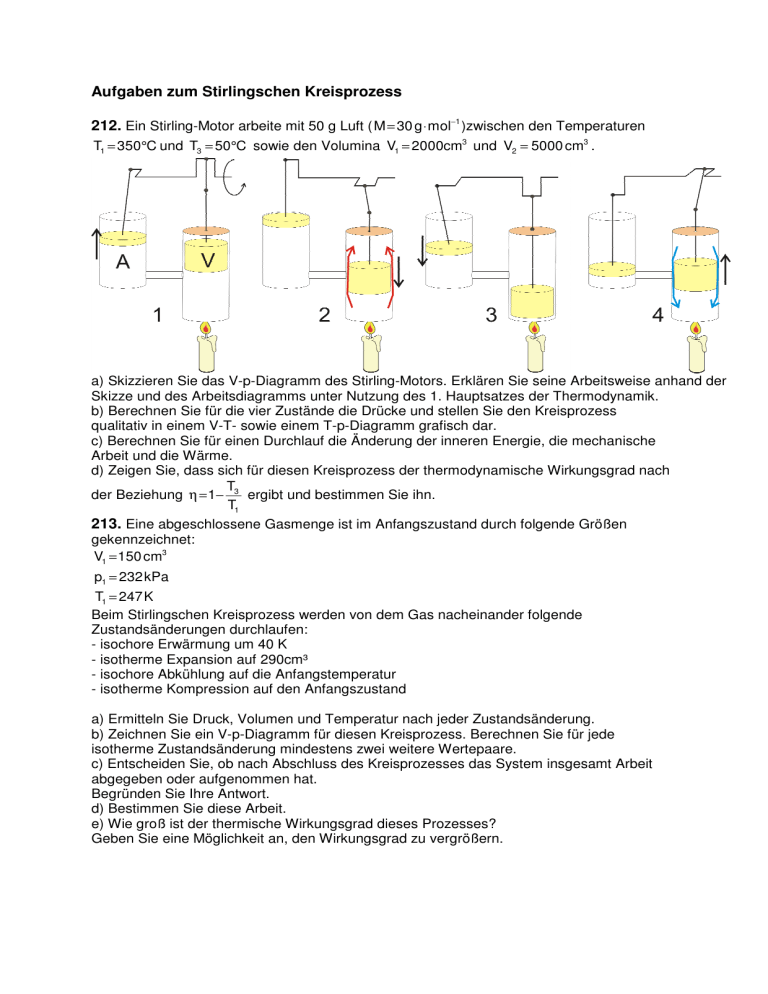
Aufgaben zum Stirlingschen Kreisprozess
212. Ein Stirling-Motor arbeite mit 50 g Luft ( M = 30 g ⋅ mol−1 )zwischen den Temperaturen
T1 = 350°C und T3 = 50°C sowie den Volumina V1 = 2000cm3 und V2 = 5000 cm3 .
a) Skizzieren Sie das V-p-Diagramm des Stirling-Motors. Erklären Sie seine Arbeitsweise anhand der
Skizze und des Arbeitsdiagramms unter Nutzung des 1. Hauptsatzes der Thermodynamik.
b) Berechnen Sie für die vier Zustände die Drücke und stellen Sie den Kreisprozess
qualitativ in einem V-T- sowie einem T-p-Diagramm grafisch dar.
c) Berechnen Sie für einen Durchlauf die Änderung der inneren Energie, die mechanische
Arbeit und die Wärme.
d) Zeigen Sie, dass sich für diesen Kreisprozess der thermodynamische Wirkungsgrad nach
T
der Beziehung η = 1− 3 ergibt und bestimmen Sie ihn.
T1
213. Eine abgeschlossene Gasmenge ist im Anfangszustand durch folgende Größen
gekennzeichnet:
V1 = 150 cm3
p1 = 232kPa
T1 = 247K
Beim Stirlingschen Kreisprozess werden von dem Gas nacheinander folgende
Zustandsänderungen durchlaufen:
- isochore Erwärmung um 40 K
- isotherme Expansion auf 290cm³
- isochore Abkühlung auf die Anfangstemperatur
- isotherme Kompression auf den Anfangszustand
a) Ermitteln Sie Druck, Volumen und Temperatur nach jeder Zustandsänderung.
b) Zeichnen Sie ein V-p-Diagramm für diesen Kreisprozess. Berechnen Sie für jede
isotherme Zustandsänderung mindestens zwei weitere Wertepaare.
c) Entscheiden Sie, ob nach Abschluss des Kreisprozesses das System insgesamt Arbeit
abgegeben oder aufgenommen hat.
Begründen Sie Ihre Antwort.
d) Bestimmen Sie diese Arbeit.
e) Wie groß ist der thermische Wirkungsgrad dieses Prozesses?
Geben Sie eine Möglichkeit an, den Wirkungsgrad zu vergrößern.
Lösungen
212.
1-2: isotherme Expansion:
Die Luft wird erwärmt und dehnt sich aus. Der
Arbeitskolben bewegt sich nach oben. Da die
Kurbelwelle für den Verdrängungskolben im
oberen Teil ist, bewegt sich dieser praktisch
nicht.
Die Luft verrichtet Arbeit. Die dafür
notwendige Energie wird durch die
Erwärmung zugeführt. Da sie sich gleichzeitig
ausdehnt, ändert sich die Temperatur nicht.
2-3: isochore Abkühlung:
Der Arbeitskolben befindet sich im oberen
Umkehrpunkt und bewegt sich praktisch
nicht. Damit bleibt das Volumen konstant.
Der Verdrängungskolben bewegt sich nach
unten und schiebt die Luft durch den
Zwischenraum zwischen Kolben und Zylinder
in den oberen Teil. Dort kühlt die Luft ab.
∆U = Q + WV
Da die Temperatur konstant bleibt, ändert
sich die innerer Energie nicht. Es gilt also
∆U = 0 und damit kann schreiben:
0 = Q12 + WV12
Q12 = − WV12
Die dem System zugeführte Wärme (positiv)
wird als Arbeit vom Motor abgegeben
(negativ).
∆U = Q + WV
Es wird keine Arbeit verrichtet, also ist
WV = 0 . Damit wird
23
∆U23 = Q23
Da eine Wärmeabgabe erfolgt, sinkt die
innere Energie und damit die Temperatur von
T1 auf T2.
Da sich der Arbeitskolben nicht bewegt, wird
keine Arbeit verrichtet.
3-4 isotherme Kompression:
Auf Grund der Energie des Schwungrades,
dass im Bild nicht mit dargestellt ist, bewegt
sich der Arbeitskolben jetzt von oben nach
unten und drückt die Luft zusammen. Die Luft
ist immer noch im kühleren Teil des
Verdrängungszylinders und gibt Wärme ab.
Die Temperatur bleibt konstant.
An der Luft wird Arbeit verrichtet, sie wird
zusammengepresst.
4-1 isochore Temperaturerhöhung
Der Verdrängungskolben bewegt sich nach
oben. Die kalte Luft strömt an ihm vorbei in
den unteren Teil und wird dort erwärmt. Der
Druckt steigt, es wird keine Arbeit verrichtet.
Zustand
1
2
3
4
V in10 −3 m3
2
5
5
2
∆U = Q + WV
Da die Temperatur konstant bleibt, ist die
Änderung der inneren Energie wieder 0.
0 = Q23 + WV23
Q23 = − WV23
Da dass System Wärme abgibt, wird daraus
−Q23 = WV23
Am System wird Arbeit verrichtet.
∆U = Q + WV
Die verrichtete Arbeit ist 0, also wird
∆U41 = Q41
Da dem System Wärme zugeführt wird, steigt
die innere Energie, also die Temperatur.
p inMPa
T in K
4,32
1,73
0,897
2,24
623
623
323
323
1-2: isotherm
Für eine isotherme Zustandsänderung gilt:
p1 ⋅ V1 = p2 ⋅ V2
Die beiden Volumina sind gegeben, aber beide Drücke sind unbekannt. Also muss noch eine
zweite Gleichung gefunden werden, damit ein Druck berechnet werden kann.
Es gilt weiterhin:
p1 ⋅ V1 = n ⋅ R ⋅ T1
n ⋅ R ⋅ T1
V1
n ist die Stoffmenge und für die gilt:
m
n=
M
Das kann man nun einsetzen und erhält eine Gleichung für den Druck bei Zustand 1:
m ⋅ R ⋅ T1
p1 =
M ⋅ V1
Damit kann der Druck berechnet werden:
50 ⋅10 −3 kg ⋅ 8,314 J ⋅ K −1 ⋅ mol−1 ⋅ 623K
p1 =
30 ⋅10 −3 kg ⋅ mol−1 ⋅ 2 ⋅10 −3 m3
p1 = 4,32MPa
p1 =
und gleich weiter der Druck für Zustand 2:
p1 ⋅ V1 = p2 ⋅ V2
p2 =
p1 ⋅ V1
V2
4,32MPa ⋅ 2 ⋅10 −3 m3
5 ⋅10−3 m3
p2 = 1,73MPa
p2 =
2-3: isochor
Das Volumen bleibt konstant und es gilt:
p 2 p3
=
T2 T3
p3 =
p2 ⋅ T3
T2
p3 =
1,73MPa ⋅ 323K
623K
p3 = 0,897MPa
3-4: isotherm
p3 ⋅ V3 = p4 ⋅ V4
p4 =
p3 ⋅ V3
V4
0,897MPa ⋅ 5 ⋅10 −3 m3
2 ⋅10−3 m3
p 4 = 2,24MPa
p4 =
V-T-Diagramm
T-p-Diagramm
Da für die beiden isochoren Zustandsänderungen gilt:
T ∼ p , müssen die beiden Geraden sich im Nullpunkt schneiden!
c) Es müssen für alle 4 Änderungen die Größen berechnet werden.
1-2 isotherm:
Die Änderung der inneren Energie ist Null.
Für eine isotherme Zustandsänderung berechnet sich die Volumenarbeit mit der Gleichung
V3
WV = −
∫ p dV
Va
Das ergibt
V 
WV = p ⋅ V ⋅ ln  e 
 Va 
Da für eine isotherme Änderung das Produkt aus p und V konstant ist, kann man die Werte
für Zustand 1 oder Zustand 2 einsetzen:
V 
WV12 = p1 ⋅ V1 ⋅ ln  2 
 V1 
 5 ⋅10 −3 m3 
WV12 = 4,32 ⋅106 Pa ⋅ 2 ⋅10 −3 m−3 ⋅ ln 
−3
3 
 2 ⋅10 m 
WV12 = − 7,93kJ
In Aufgabe a) wurde gezeigt, dass
Q12 = − WV12
Damit wird vom System 7,93 kJ Arbeit verrichtet und 7,93 kJ Wärme aufgenommen.
2-3 isochor:
Vom System wird Wärme abgegeben, es gilt:
Q = m ⋅ C V ⋅ ∆T
und eingesetzt:
Q23 = 0,05kg ⋅ 0,72
kJ
⋅ ( −300K )
kg ⋅ K
Q23 = − 10,8kJ
Das System gibt 10,8 kJ Wärme ab.
3-4 isotherm:
Das wird wieder wie bei der Zustandänderung 1-2 gerechnet:
V 
WV34 = p3 ⋅ V3 ⋅ ln  4 
 V3 
 2 ⋅10−3 m3 
WV34 = 0,897 ⋅106 Pa ⋅ 5 ⋅10 −3 m−3 ⋅ ln 
3 
−3
 5 ⋅10 m 
WV34 = 4,11kJ
Diese Arbeit von 4,11 kJ muss in das System gesteckt werden. Dabei wird genau dieser
Betrag in Form von Wärme abgegeben.
4-1 isochor
Es wird wie bei der Änderung 2-4 gerechnet und man erhält eine Wärme von 10,8 kJ, die
das System aufnehmen muss.
d) Für eine Maschine, in der ein Kreisprozess abläuft, gilt allgemein für de Wirkungsgrad:
Q + Qab
η = zu
Q zu
Die in den Änderungen 2-3 und 4-1 auftretenden Wärmengen heben sich auf, so dass nur
noch die Änderungen 1-2 und 3-4 betrachtet werden müssen. Da entsprechen die Wärmen
den verrichteten Arbeiten.
V 
V 
−p1 ⋅ V1 ⋅ ln  2  − p3 ⋅ V3 ⋅ ln  4 
 V1 
 V3 
η=
V 
−p1 ⋅ V1 ⋅ ln  2 
 V1 
Nun kann man ersetzten:
p ⋅ V = n ⋅R ⋅ T
V 
V 
−n ⋅ R ⋅ T1 ⋅ ln  2  − n ⋅ R ⋅ T3 ⋅ ln  4 
 V1 
 V3 
η=
V 
−n ⋅ R ⋅ T1 ⋅ ln  2 
 V1 
V 
V 
−T1 ⋅ ln  2  − T3 ⋅ ln  4 
 V1 
 V3 
η=
V 
−T1 ⋅ ln  2 
 V1 
Da gilt:
V 
V 
ln  4  = − ln  3 
 V3 
 V4 
und
V1 = V4
V2 = V3
wird
V 
V 
−T1 ⋅ ln  2  + T3 ⋅ ln  2 
 V1 
 V1 
η=
V 
−T1 ⋅ ln  2 
 V1 
gekürzt:
−T + T
η= 1 3
−T1
η = 1−
T3
T1
Mit den gegebenen Temperaturen erhält man einen maximalen Wirkungsgrad von 48%. In
der Realität ist er kleiner, da in diese Rechnung keine Reibungsverluste eingegangen sind.
213.
a) Die vier Zustände werden in einer Tabelle dargestellt:
Zustand
p in kPa
V in cm³
1
232
150
2
270
150 (isochor)
3
140
290
4
120
290
T in K
247
287 (247 + 40)
287
247
Der Druck beim Übergang von Zustand 1 nach Zustand 2 berechnet sich mit
p1 T1
=
p2 T2
T2
⋅ p1
T1
Beim Übergang 2 nach 3 gilt für die isotherme Zustandsänderung:
p2 =
p2 V3
=
p3 V2
V2
⋅ p2
V3
Beim Übergang 3 nach 4 gilt:
p3 T3
=
p 4 T4
p3 =
p4 =
T4
⋅ p3
T3
b) Für die isothermen Zustandsänderungen werden für selbst gewählte Volumen die Drücke
berechnet. Dazu wird der in Aufgabe a) gezeigte Zusammenhang zwischen Druck und
Volumen für die isotherme Zustandsänderung verwendet:
p ⋅ V = konst.
Übergang 2->3 (isotherme Expansion)
V in cm³ 180 210 240 270
p in kPa 225 193 169 150
Übergang 4->1 (isotherme Kompression)
V in cm³ 180 210 240 270
p in kPa 193 166 145 129
Kreisdiagramm
c) Die von einem System abgegeben Arbeit ist allgemein die Fläche unter der Kurve im V-pDiagramm.
Der Vorgang 2->3 ist eine Expansion, also der Vorgang, bei dem das System Arbeit
verrichtet. Der Übergang 4->1 ist eine Kompression, am System muss Arbeit verrichtet
werden.
Der Betrag des Anteils 2 -> 3 ist größer als der Betrag des Anteils 4 -> 1, insgesamt wird
also vom System Arbeit abgegeben.
d) Damit ist auch klar, wie sich diese Arbeit berechnen lässt. Es muss die Arbeit für den
Übergang 2->3 berechnet werden. Davon zieht man die Arbeit ab, die beim Übergang 4->1
wieder in das System hinein gesteckt wird. Diese Arbeit wird bei einem Motor z.B. in einer
Schwungscheibe gespeichert.
Für eine isotherme Zustandänderung berechnet sich die Volumenarbeit nach der Gleichung:
V
W = p A ⋅ VA ⋅ ln A
VE
A kennzeichnet den Anfang und E das Ende.
Gibt ein System Arbeit ab, hat die Arbeit ein negatives Vorzeichen. Nimmt es Arbeit auf, wird
das Vorzeichen automatisch positiv, da das Endvolumen kleiner ist als das Anfangsvolumen.
Die Gesamtarbeit ist dann also:
W = W23 + W41
Plus deshalb, weil sich die Vorzeichen bei der Berechnung ergeben.
V
V
W = p2 ⋅ V2 ⋅ ln 2 + p 4 ⋅ V4 ⋅ ln 4
V3
V1
W = 2,7 ⋅105 Pa ⋅1,5 ⋅10 −4 m3 ⋅ ln
150 cm3
290 cm3
5
−4
3
+
1,2
⋅
10
Pa
⋅
2,9
⋅
10
m
⋅
ln
290 cm3
150 cm3
W = − 26.7 J + 22,9 J
W = − 3,8 J
Der Stirlingmotor gibt bei jeder Umdrehung 3,8 J Arbeit ab,
e) Der thermische Wirkungsgrad eines Kreisprozesses wird durch die beiden Temperaturen
bestimmt. Es gilt:
T
η = 1− 1
T2
247K
287K
η = 0,14
η = 1−
η = 14%
Der Wirkungsgrad kann nur durch die Änderungen der Temperaturen erhöht werden.
Entweder wird die große Temperatur weiter erhöht oder die niedrige Temperatur weiter
verkleinert.