pch_ausarbeitung

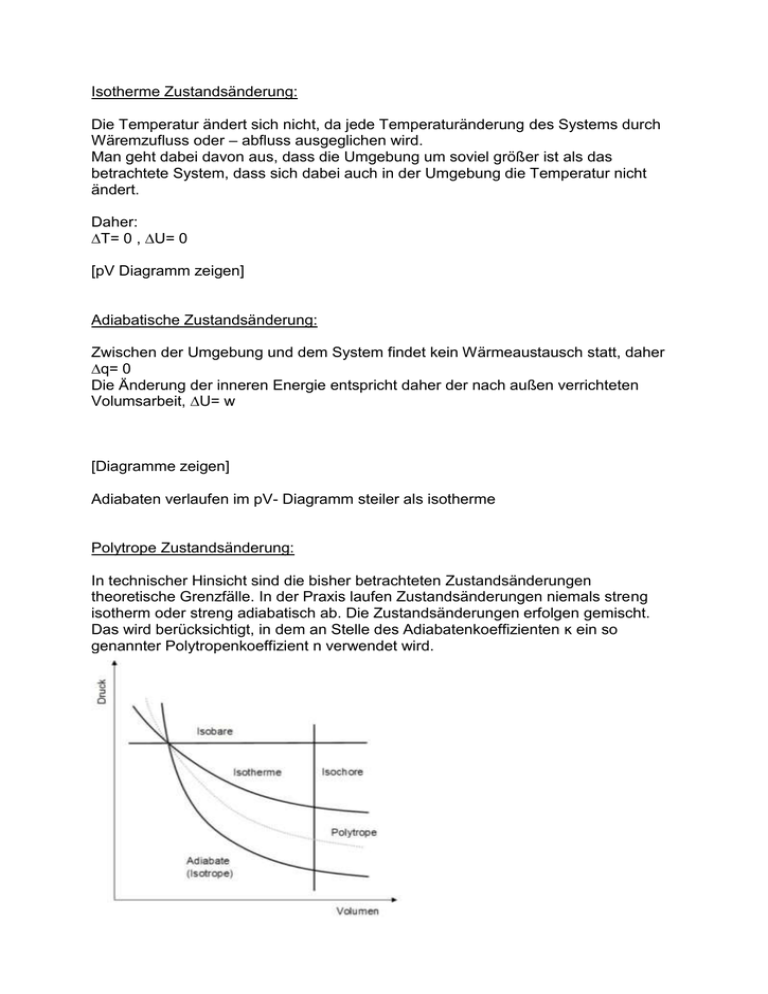
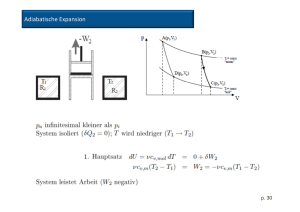
Isotherme Zustandsänderung:
Die Temperatur ändert sich nicht, da jede Temperaturänderung des Systems durch
Wäremzufluss oder – abfluss ausgeglichen wird.
Man geht dabei davon aus, dass die Umgebung um soviel größer ist als das
betrachtete System, dass sich dabei auch in der Umgebung die Temperatur nicht
ändert.
Daher:
∆T= 0 , ∆U= 0
[pV Diagramm zeigen]
Adiabatische Zustandsänderung:
Zwischen der Umgebung und dem System findet kein Wärmeaustausch statt, daher
∆q= 0
Die Änderung der inneren Energie entspricht daher der nach außen verrichteten
Volumsarbeit, ∆U= w
[Diagramme zeigen]
Adiabaten verlaufen im pV- Diagramm steiler als isotherme
Polytrope Zustandsänderung:
In technischer Hinsicht sind die bisher betrachteten Zustandsänderungen
theoretische Grenzfälle. In der Praxis laufen Zustandsänderungen niemals streng
isotherm oder streng adiabatisch ab. Die Zustandsänderungen erfolgen gemischt.
Das wird berücksichtigt, in dem an Stelle des Adiabatenkoeffizienten ĸ ein so
genannter Polytropenkoeffizient n verwendet wird.
Cannonischer Kreisprozess:
In einem thermodynamischen Kreisprozess ist die Gesamtänderung einer
Zustandsfunktion gleich Null.
Der ideale Fall, ein Kreisprozess ausschließlich aus Isothermen und Adiabaten ist
der so genannte Carnot- Prozess. Er besteht aus vier reversiblen Teilschritten:
1. Schritt: Reversible isotherme Expansion
Durch die Expansion wird Arbeit an der Umgebung verrrichtet
Die Innere Engergie ändert sich nicht, da Wärme von außen zugeführt
wird. ∆U= 0
2. Schritt: Reversible adiabatische Expansion
Das System gibt keine Wärme an die Umgebung ab: q= 0
Die Entropieänderung ist Null: ∆S= 0
Die Temperatur fällt von ab
3. Schritt: Reversible isotherme Kompression
Durch die Kompression wird Arbeit am System verrichtet
Die Innere Energie ändert sich nicht, da Wärme nach außen an die
kalte Umgebung abgeführt wird. ∆U= 0
4. Schritt: Reversible adiabatische Kompression
Das System nimmt keine Wärme von der Umgebung auf: q= 0
Die Entropieänderung ist Null: ∆S= 0
Die Temperatur steigt an
Da q= 0 ist entspricht w= ∆U
Die Gesamänderung der Entropie ist gleich Null, da die Entropie eine
Zustandsfunktion ist.
Wirkungsgrad:
Die dem warmen Reservoir entnommene Wärmemenge entspricht der Arbeit bei der
isothermen Expansion(q= -w), Für den Wirkungsgrad eingesetzt ergibt das:
η= ∆T/TW
Wärmekraftmaschine:
Aus Wärme kann nur dann mechanische Arbeit gewonnen werden wenn ein
freiwilliger Vorgang abläuft bei dem die Gesamtenthropie zunimmt. Ein solcher
Vorgang kann nur der Transport von Wärme von einem warmen zu einem kalten
Reservoir sein.
Die dem warmen Reservoir entnommenen Wärme bewirkt eine geringere
Entropieabnahme als dieselbe Wärme die dem kalten Reservoir zugeführt wird an
Entropiezunahme bewirkt
q/T
Wirkungsgrad von Wärmekraftmaschinen:
ist das Verhältnis von Ertrag zu Aufwand
η= geleistete Arbeit/aufgenommene Wärme
Die aufgenommene Wärme ist die Wärme die der Maschine durch den Brennstoff
zugeführt werden muss. Durch die Verbrennung und die Bewegung der Maschine
kommt es jedoch zu zahlreichen Energieverlusten, der Wirkungsgrad ist daher in der
Praxis nicht erreichbar, er ist die obere theoretische Grenze des Wirkungsgrades für
jede mögliche Wärmekraftmaschine.
Da der Wirkungsgrad gegen 1 strebt wenn die Temperatur des klaten Reservoirs
gegen Null geht oder die Temperatur des warmen Reservoirs unendlich groß wird,
sind folgende Verhältnisse anzustreben:
 Eine möglichst große Temperaturdifferenz zwischen dem warmen und kaklten
Reservoir
 Eine möglichst niedrige Temperatur des kalten Reservoirs