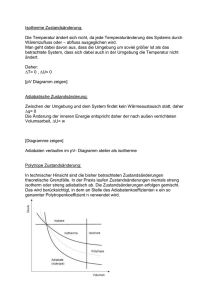
10 v , 〉〈v und max v

45) Die Temperatur einer Schmelze soll bestimmt werden. Dazu wird eine Platinkugel
(spezifische Wärme 130 J kg-1 K-1) mit Masse 0.35 kg in die Schmelze gegeben und danach in
einem Kalorimeter abgekühlt, in dem sich 1 Liter Wasser mit Temperatur 10°C befindet.
Nachdem das thermische Gleichgewicht erreicht ist, misst man eine Wassertemperatur von
12°C. Wie heiß ist die Schmelze?
46) "Gewicht" eines idealen Gases. Gegeben sei ein dünner Ballon von Durchmesser d. Er
werde mit einem idealen Gas gefüllt und im Vakuum auf eine Waage gelegt.
• Welches "Gewicht" des Ballons wird gemessen? Zeigt die Waage nicht überhaupt Null
an?
• Welches "Gewicht" ergibt sich, wenn Sie für das ideale Gas Normalbedingungen
(T=25 oC, p~1 atm) und d ~ 1 m voraussetzen?
Anleitung: Bedenken Sie, dass die idealen Gasteilchen untereinander überhaupt nicht
wechselwirken und auch nur beim Aufprall auf die Hülle des Ballons auf diesen Kraft
übertragen können. Nehmen Sie vereinfachend einen würfelförmigen "Ballon" an!
Vernachlässigen Sie auch das Gewicht seiner Hülle.
47) Nehmen Sie an, Sie möchten einen Wetterballon so hoch wie möglich steigen lassen. Mit
der Höhe nimmt der Druck in der Atmosphäre ab (barometrische Höhenformel), also dehnt
sich das Helium im Ballon aus. Der Ballon wird am Boden daher nur zu einem Teil befüllt
(der Rest der Hülle enthält nur Luft). Binden sie den Ballon unten zu, bevor Sie ihn
aufsteigen lassen, oder lassen Sie ihn offen? Warum?
48) Bei der Ableitung der barometrischen Höhenformel wird angenommen, dass die
Temperatur über die gesamte betrachtete Höhe konstant bleibt. In der Realität nimmt die
Temperatur mit zunehmender Höhe ab (in trockener Luft ca. 1°C / 100 m)
a) Warum muss in einem kompressiblen Medium im Schwerefeld die Temperatur mit
der Höhe abnehmen? (Betrachten Sie ein „Luftpaket“ mit einer fiktiven Grenze, über
die im betrachteten Zeitraum weder Wärme- noch Materialtransport stattfindet)
b) Warum kann man bei relativ geringen Höhenunterschieden (Ann: ca. 1000 m)
trotzdem relativ gut mit der barometrischen Höhenformel arbeiten?
c) Wie ändert sich die Temperaturabnahme mit der Höhe (qualitativ!), wenn die Luft
sehr viel Wasserdampf enthält?
49) Auf wieviel Grad erhitzt sich die Luft in einem Dieselmotor vor der Einspritzung bei der
adiabatischen Kompression (V1/V2 = 30, Ausgangsdruck und Temperatur: 1 bar, 20°C)
50) Die Analyse einer Gasmischung ergab folgende molekulare Zusammensetzung:
N2 = 60 %, CO2 = 20 %, O2 = 20 %. Wie groß sind die Massenanteile und die molare Masse
der Mischung? Wie groß ist die Masse von 100 m3 Gas bei 0.75 bar und 0°C ?
51) Geben Sie ein ungefähres Bild der Maxwell-Boltzmann-Verteilung für zwei verschiedene
Temperaturen. Berechnen Sie ⟨ v 2 ⟩ , ⟨v ⟩ und v max für He und N2 für 100 K, 300 K und
1000 K. Was bedeuten die verschiedenen Geschwindigkeiten?
52) In einem geschlossenen Behälter mit dem Volumen V = 10 Liter und einer Temperatur
von 300 K befindet sich ein Gemisch von 16 g Helium und 10 g molekularem Wasserstoff.
Wie groß ist der Druck auf die Behälterwände? Welches Gas hat den größeren Partialdruck
und warum?
53) Eine ideale (reversibel arbeitende) Wärmepumpe soll Wärme für Heizzwecke bei einer
Temperatur von T+ = 350 K liefern. Ein (unerschöpflicher) See mit der Wassertemperatur T= 280 K dient als unteres Wärmereservoir. Wie groß ist die Leistungsziffer und wie viel
Übungen zu Einführung in die Physik I, WS 09/10
10
Arbeit ist pro Joule bei T+ abgegebener Wärme aufzuwenden? Erklären Sie generell, was eine
Wärmepumpe ist und wie sie funktioniert!
54) Wirkungsgrad von Dampfmaschinen:
Eine Dampfmaschine arbeitet zwischen den Temperaturen 100 °C und 200 °C.
a) Wie groß ist der theoretische Wirkungsgrad?
b) Welche Arbeit leistet die Maschine, wenn sie dem heißeren Reservoir 12000 J in Form von
Wärme entnimmt?
c) Berechnen Sie die Änderung der Entropie pro Zyklus, wenn die gesamte vom heißen
Reservoir aufgenommene Wärmemenge an das kalte Reservoir abgegeben wird!
55) Die Wirkungsweise eines Motors sei – idealisiert – durch folgende Prozesse beschrieben:
a) v1 → v2 (adiabatisches Verdichten, wobei p1 → p2; Verdichtungsverhältnis v1/v2 = 10)
b) p2 → p3 (v = const., Verbrennung unter Freisetzung von Q)
c) v2 → v1 (adiabatisches Expandieren, wobei p3 → p4)
d) p4 → p1 (v = const, sodass der Ausgangszustand erreicht wird).
Berechnen Sie den Wirkungsgrad Arbeit/(Verbrennungswärme Q). (Es wird cV = const
angenommen).
Übungen zu Einführung in die Physik I, WS 09/10
11