Binomialverteilung - Hochschule Niederrhein

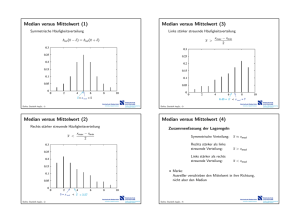
Binomialverteilung (1)
Binomialverteilung (3)
Situation:
Eigenschaften (Forts.):
• Münze wird n mal geworfen
• je Wurf 1“ mit W’keit p oder 0“ mit W’keit q = (1 − p)
”
”
• gefragt: W’keit für Auftreten von k Einsen
• für p = 0.5 symmetrisch um k = np = n/2
P(k)
• insgesamt zwei Parameter: n und p
0.2
Wahrscheinlichkeit:
0.15
n k n−k
P(“k Einsen”) =
p q
k
0.1
Normierung:
• k kann Werte 0, 1, . . . , n annehmen
⇒ Summe über W’keiten aller k Werte muss Eins sein
• ergibt sich aus binomischer Formel:
n X
n k n−k
p q
= (p + q)n = (p + 1 − p)n = 1n = 1
k
k=0
Hochschule Niederrhein
University of Applied Sciences
Dalitz: Statistik kap3b. -1-
0.05
0
0
2
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
4
6
P(4) = P(6)
n = 10
p = 0.5
8
Elektrotechnik
und Informatik
Faculty of Electrical Engineering
and Computer Science
Binomialverteilung (2)
10
k
Hochschule Niederrhein
University of Applied Sciences
Dalitz: Statistik kap3b. -3-
Eigenschaften (Forts.):
• maximale Wahrscheinlichkeit für k ≈ np
• Verteilungen für p und (1 − p) sind gespiegelt an n/2
P(k)
Pp (k)
0.25
0.2
0.15
0.1
0.05
0
−2
0
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
2
np = 2
0.3
n = 10
p = 0.2
P0.8 (k)
P0.2 (k)
n = 10
0.25
000
111
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
0.2
0.15
0.1
0.05
0
4
6
8
10
0
k
Hochschule Niederrhein
Dalitz: Statistik kap3b. -2-
Faculty of Electrical Engineering
and Computer Science
Binomialverteilung (4)
Eigenschaften:
0.3
Elektrotechnik
und Informatik
University of Applied Sciences
Elektrotechnik
und Informatik
Faculty of Electrical Engineering
and Computer Science
2
000
111
111
000
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
000
111
4
6
8
Pp (k) = P1−p (n−k)
10
k
Hochschule Niederrhein
Dalitz: Statistik kap3b. -4-
University of Applied Sciences
Elektrotechnik
und Informatik
Faculty of Electrical Engineering
and Computer Science