Median versus Mittelwert (1) Median versus Mittelwert (2) Median
Werbung

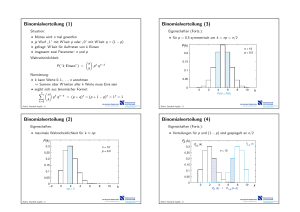
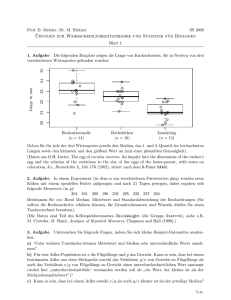
Median versus Mittelwert (1) Median versus Mittelwert (3) Symmetrische Häufigkeitsverteilung Links stärker streuende Häufigkeitsverteilung hrel (x − δ) = hrel (x + δ) x > 0.3 xmax − xmin 2 0.3 0.25 0.25 0.2 0.2 0.15 0.15 0.1 0.1 0.05 0.05 0 0 2 4 6 8 0 10 0 x = x med = 5 2 4 6 8 10 6.43 = x < x med = 7 Hochschule Niederrhein University of Applied Sciences Dalitz: Statistik kap2c. -1- Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science Median versus Mittelwert (2) Hochschule Niederrhein University of Applied Sciences Dalitz: Statistik kap2c. -3- Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science Median versus Mittelwert (4) Rechts stärker streuende Häufigkeitsverteilung Zusammenfassung der Lageregeln xmax − xmin x < 2 0.3 Symmetrische Verteilung: x ≈ xmed Rechts stärker als links streuende Verteilung: x > xmed Links stärker als rechts streuende Verteilung: x < xmed 0.25 0.2 0.15 • Merke: 0.1 Ausreißer verschieben den Mittelwert in ihre Richtung, nicht aber den Median 0.05 0 0 2 4 6 8 10 3 = x med < x = 3.57 Hochschule Niederrhein Dalitz: Statistik kap2c. -2- University of Applied Sciences Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science Hochschule Niederrhein Dalitz: Statistik kap2c. -4- University of Applied Sciences Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science Weitere Kenngrößen (1) Weitere Kenngrößen (3) Zwei Verteilungen mit gleichem Mittelwert und Median: (die Balken sind leicht verschoben, damit sie unterscheidbar sind) Naheliegendes Streuungsmaß: n 1 X |xi − x| n 0.35 i=1 0.3 • mittlerer Abstand vom Mittelwert 0.25 0.2 • wird jedoch nicht verwendet 0.15 I Betragsfunktion hat Knick (nicht differenzierbar) ⇒ keine analytische Behandlung möglich ⇒ keine Näherungsformeln/Fehlerfortpflanzungsgesetz möglich I taucht in theoretischen Rechnungen nicht als natürliche“ ” Größe auf (z.B. kein Parameter in Normalverteilung) 0.1 0.05 0 x = x med Wodurch unterscheiden sich diese Verteilungen? Hochschule Niederrhein University of Applied Sciences Dalitz: Statistik kap2c. -5- Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science Weitere Kenngrößen (2) Hochschule Niederrhein University of Applied Sciences Dalitz: Statistik kap2c. -7- Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science Weitere Kenngrößen (4) Deswegen betrachtet man: 0.35 n 1 X (xi − x)2 n 0.3 mehr Werte weichen vom Mittelwert ab 0.25 i=1 0.2 I mittlerer quadratischer Abstand vom Mittelwert I analytische Funktion I gewichtet starke Abweichungen stärker 0.15 0.1 0.05 0 • führt zum Begriff der Varianz x • bei der einen Verteilung sind stärkere Abweichungen • alternatives Streuungsmaß sind Quantile vom Mittelwert häufiger • Gesucht: Maß für die Konzentration der Werte um Mittelwert Hochschule Niederrhein Dalitz: Statistik kap2c. -6- University of Applied Sciences Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science Hochschule Niederrhein Dalitz: Statistik kap2c. -8- University of Applied Sciences Elektrotechnik und Informatik Faculty of Electrical Engineering and Computer Science