H. Stichtenoth WS 2005/06 Lösungsvorschlag für das 3
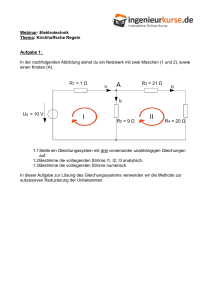
Werbung

H. Stichtenoth
WS 2005/06
Lösungsvorschlag für das 3. Übungsblatt
Aufgabe 11: Der gesuchte Unterraum U ist die lineare Hülle von v1 und v2 (siehe Def. 5.13
und Bsp. 5.15b), d. h.
U := Span{v1 , v2 } = {v ∈ R3 : v = λ1 · v1 + λ2 · v2 , λ1 , λ2 ∈ R} =
2
−1
3
3
+ λ2 · −6 , λ1 , λ2 ∈ R .
=
v ∈ R : λ1 ·
−2
1
Aber v2 = −2v1 , also kann man v als v = (λ1 − 2λ2 ) · v1 schreiben, d. h.
−1
Span{v1 , v2 } = v ∈ R3 : v = λ · 3 , λ ∈ R = Span{v1 }.
1
Analog v1 = − 12 v2 , und weiter v = − 12 · λ1 + λ2 · v2 , d. h.
2
Span{v1 , v2 } = v ∈ R3 : v = λ · −6 , λ ∈ R = Span{v2 }.
−2
Der Unterraum U ist also eine Gerade im R3 , zu der der Ursprung des Koordinatensystems
gehört und die durch den Vektor v1 (bzw. v2 ) bestimmt ist.
Aufgabe 12: Zu zeigen ist, dass R3 ⊆ U = Span{v1 , v2 , v3 }.
Sei v = (x1 , x2 , x3 )t ein beliebiger Vektor des R3 . Wir wollen v als Linearkombination von
Vektoren {v1 , v2 , v3 } darstellen, d. h. wir müssen die reellen Zahlen λ1 , λ2 , λ3 finden, so dass
1
1
0
x1
v = x2 = λ1 · v 1 + λ2 · v 2 + λ3 · v 3 = λ1 · 1 + λ2 · 0 + λ3 · 1 .
0
1
1
x3
Dies ist äquivalent mit dem folgenden Gleichungssystem
λ2 + λ3 = x1
λ1 +
+ λ3 = x2
λ1 + λ2
= x3 ,
wobei λ1 , λ2 , λ3 Unbekannten und x1 , x2 , x3 die gegebenen rechte Seiten sind.
Man kann leicht feststellen, dass das Gleichungssystem lösbar ist und
1
(−x1 + x2 + x3 ) ,
2
die eindeutige Lösung ist.
λ1 =
λ2 =
1
(x1 − x2 + x3 ) ,
2
λ3 =
1
(x1 + x2 − x3 )
2
Folglich, jeder Vektor des R3 ist als Linearkombination von Vektoren {v1 , v2 , v3 } mit den
oben angegebenen Koeffizienten darstellbar, d. h. R3 ⊆ U = Span{v1 , v2 , v3 }.
Aufgabe 13:
1
2
a) Wir suchen λ1 , λ2 ∈ R, so dass v3 = λ1 · v1 + λ2 · v2 , d. h.
3
−1
3
= λ1 ·
+ λ2 ·
.
5
3
−2
Dies ergibt ein lineares Gleichungssystem mit den Unbekannten λ1 und λ2 :
−λ1 + 3 · λ2 = 3
(∗)
3 · λ1 − 2 · λ2 = 5.
(∗∗)
Aus (∗) bekommt man λ1 = 3λ2 − 3 und setzt man dies in (∗∗) ein:
3 (3λ2 − 3) − 2λ2 = 5
⇐⇒
9λ2 − 9 − 2λ2 = 5 ⇐⇒
⇐⇒
7λ2 = 5 + 9 = 14 ⇐⇒ λ2 = 2.
Daraus folgt λ1 = 3 · 2 − 3 = 3.
Somit ist:
v3 = 2v1 + 3v2 .
b) Nein! Mit a) erhält man
2v1 + 3v2 − v3 = 0
und diese Darstellung der Null ist nicht trivial.
c) Man muss zeigen, dass die Null nur trivial darstellbar ist.
Nehmen wir an, dass für gewisse λ1 , λ2 ∈ R:
0
3
−1
.
=
+ λ2 ·
λ1 ·
0
−2
3
Dies ergibt wieder ein lineares (homogenes) Gleichungssystem mit den Unbekannten
λ1 und λ2 :
−λ1 + 3 · λ2 = 0
3 · λ1 − 2 · λ2 = 0,
dessen Lösung λ1 = λ2 = 0 genauso bestimmt wird, wie im a). Somit sind diese
Vektoren linear unabhängig.
Aufgabe 14: Wir berechnen zuerst die Vektoren
−2
3
1
und
=
−
v1 − v2 =
3
4
7
v1 + v2 =
1
7
+
3
4
=
4
11
.
Nehmen wir jetzt an, dass für gewisse λ1 , λ2 ∈ R:
0
4
−2
.
=
+ λ2 ·
λ1 ·
0
11
3
Dies ergibt ein lineares (homogenes) Gleichungssystem mit den Unbekannten λ1 und λ2 :
−2 · λ1 + 4 · λ2 = 0
3 · λ1 + 11 · λ2 = 0,
dessen Lösung λ1 = λ2 = 0 genauso bestimmt wird, wie in Aufgabe 13a). Somit sind diese
Vektoren linear unabhängig.
Diese Folgerung gilt für beliebige linear unabhängige Vektoren v1 und v2 :
Nehmen wir an, dass
λ1 · (v1 − v2 ) + λ2 · (v1 + v2 ) = 0
für gewisse reelle Zahlen λ1 , λ2 . Wir wollen zeigen, dass daraus λ1 = λ2 = 0 folgt.
3
Wir formen die obige Gleichung um, indem wir die Rechengesetze für Vektoradditon und
Skalarmultiplikation benutzen:
(λ1 + λ2 ) v1 + (λ2 − λ1 ) v2 = 0.
Die Vektoren v1 und v2 sind aber linear unabhängig, d. h.
λ1 + λ2 = 0
−λ1 + λ2 = 0.
Dieses lineare Gleichungssystem lösen wir genauso, wie in den vorherigen Aufgaben, und
bekommen wir als Lösung
λ1 = 0
und
λ2 = 0.
Daraus folgt, dass auch die Vektoren v1 − v2 und v1 + v2 linear unabhängig sind.
Aufgabe 15: Nehmen wir an, dass für gewisse reelle Zahlen λ1 , λ2 , λ3 gilt:
λ1 · v1 + λ2 · v2 + λ3 · v3 = 0,
d. h.
1
−1
−1
λ1 2 + λ2 2 + λ3 −2 = 0.
3
3
1
Dies ergibt ein lineares Gleichungssystem mit drei
λ1 , λ2 , λ3 :
λ2 +
λ3 =
−λ1 −
2 · λ1 + 2 · λ2 − 2 · λ3 =
λ1 + 3 · λ2 + 3 · λ3 =
Gleichungen und drei Unbekannten
0
0
0
(∗)
(∗∗)
(∗ ∗ ∗)
Addiert man jetzt zu der zweiten Gleichung zweifaches der ersten Gleichung ((∗∗) + 2 · (∗)),
bekommt man eine triviale Gleichung 0 = 0. Das heisst, man muss ein lineares Gleichungssystem mit zwei Gleichungen und drei Unbekannten λ1 , λ2 , λ3 lösen:
−λ1 −
λ2 +
λ3 = 0
λ1 + 3 · λ2 + 3 · λ3 = 0
Die Unbekannte λ3 = C kann jetzt mit beliebigem Wert C ∈ R belegt werden. Werden
die Ausdrücke mit C auf die rechte Seite gebracht, so ensteht ein lineares Gleichungssystem
mit zwei Gleichungen und zwei Unbekannten λ1 , λ2 :
−λ1 −
λ2 = −C
λ1 + 3 · λ2 = −3C
das wird genauso, wie in den vorherigen Aufgaben, gelöst:
λ1 = 3C
und
λ2 = −2C.
Folglich, das erste Gleichungssystem hat unendlich viele Lösungen mit einem Parameter:
λ1 = 3C,
λ2 = −2C,
λ3 = C
mit C ∈ R,
d. h. die Vektoren v1 , v2 , v3 sind linear abhängig.
Eine nichttriviale Linearkombination von v1 , v2 , v3 , die dem Nullvektor gleich ist, erhält
man z. B. für C = 1:
3 · v1 − 2 · v2 + v3 = 0.
4
Aufgabe 16: Es reicht zu zeigen, dass die drei Vektoren v1 , v2 , v3 ∈ R3 linear unabhängig
sind, weil dim R3 = 3.
Dazu nehmen wir an, dass für gewisse reelle Zahlen λ1 , λ2 , λ3 gilt:
λ1 · v1 + λ2 · v2 + λ3 · v3 = 0,
d. h.
1
1
1
λ1 0 + λ2 1 + λ3 1 = 0.
1
0
0
Dies ergibt ein lineares Gleichungssystem mit drei Gleichungen und drei Unbekannten
λ1 , λ2 , λ3 :
λ1 + λ2 + λ3 = 0
λ2 + λ3 = 0
λ3 = 0,
dessen Lösung λ1 = λ2 = λ3 = 0 leicht zu berechnen ist.
Folglich sind die Vektoren v1 , v2 , v3 linear unabhängig und sie bilden eine Basis des R3 .
Aufgabe 17: Zuerst müssen wir den Kern von ϕ bestimmen, d. h. wir müssen alle Vektoren
x = (x1 , x2 , x3 )t finden, die die Gleichung
x1
ϕ x2 = 0
x3
erfüllen. Dies ergibt ein lineares Gleichungssystem mit drei Gleichungen und drei Unbekannten x1 , x2 , x3 :
x3 = 0
(∗)
x1 + 2 · x2 −
x2 +
x3 = 0
(∗∗)
x +
x2 − 2 · x3 = 0
(∗ ∗ ∗).
1
Subtrahiert man von der ersten Gleichung die Summe von der zweiten und dritten Gleichung
((∗) − ((∗ ∗ ∗) + (∗∗))), so bekommt man eine triviale Gleichung 0 = 0. Das heisst, man muss
das Gleichungssystem mit zwei Gleichungen und drei Unbekannten x1 , x2 , x3 lösen:
x2 +
x3 = 0
x1 + x2 − 2 · x3 = 0.
Die Unbekannte x3 = C kann jetzt mit beliebigem Wert C ∈ R belegt werden. Werden die
Ausdrücke mit C auf die rechte Seite gebracht, so ensteht ein lineares Gleichungssystem mit
zwei Gleichungen und zwei Unbekannten x1 , x2 :
x2 = −C
x1 + x2 = 2C,
dessen Lösung
x1 = 3C
und
x2 = −C
leicht zu berechnen ist.
Folglich, das erste Gleichungssystem hat unendlich viele Lösungen mit einem Parameter:
x1 = 3C,
x2 = −C,
x3 = C
mit C ∈ R,
5
und
3C
Kern ϕ = x = −C :
C
3
C ∈ R = x = C · −1 :
1
Das heisst, dim Kern ϕ = 1 und (3, −1, 1)t ist ein Basisvektor des Kernes.
C∈R .
Aufgabe 18:
a) Zwei Matrizen sind gleich genau dann, wenn sie gleichdimensioniert sind und wenn
die Elemente an den entsprechenden Positionen gleich sind.
Die erste und zweite Matrix sind zwar gleichdimensioniert (4 × 1), aber in der ersten
Matrix ist 1 an der Stelle (4, 1) und in der zweiten Matrix – an der Stelle (1, 1).
Die dritte und vierte Matrix sind auch gleichdimensioniert (1× 4), aber in der dritten
Matrix ist 1 an der Stelle (1, 4) und in der vierten Matrix – an der Stelle (1, 1).
b) Die gegebenen Matrizen sind gleichdimensioniert (2 × 4), also sie sind gleich, wenn
die Elemente an den entsprechenden Positionen gleich sind, insbesondere
x2 − 1 = 0
=⇒
x = −1
oder
x = 1,
2
(x + 1) = 4
=⇒
x = −3
oder
x=1
Folglich: die Matrizen sind gleich für x = 1.