Mathematik - Duden Schulbuch
Werbung

Mathematik
Gymnasium
Übungsaufgaben mit Lösungen
ch
Nordrhein-Westfalen
Bu
Mathematik 7 Gymnasium NRW
7
CD
m
-ROM i
12.12.2007 10:20:43 Uhr
Fit in Mathe 1
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Fit in Mathe
1. Rechne vorteilhaft.
a) 75 + 16 + 25 + 84
e) 32 · 68 · 0 · 12
i) (270 – 54) : 9
b) 87 + 21 – 17 + 39
f ) 8 · (15 + 25)
j) (– 4) · 21 · (– 5)
c) 4 · 21 · 25
g) 28 : (7 – 3)
k) 18 · 9 · (–1)
d) 15 · 17 : 5
h) (75 + 9) : 12
l) (13 + 5) · 25 · 4
2. Löse die Aufgaben.
a) 2,7 · 4
e) 19,8 : 11
i) 0,371 · 100
b) 0,34 · 1,1
f ) 37,5 : 25
j) 16,4 : 10
c) 3,6 : 9
g) 4,85 · 10
k) 16,4 : 100
d) 15,2 : 4
h) 4,85 · 100
l) 2,5 : 100
3. Gib an, welchen Bruchteil von der gesamten Fläche der gefärbte Teil einnimmt.
a)
b)
c)
d)
e)
f)
4. Vergleiche. Setze <, > oder = ein.
a) 63
104
b) 2,3
0,035
e) 0,35
2
}3
f)
2,03
c) 0,43
5
}3
g)
5. a) Erweitere die Brüche.
2
}3 = }9 ;
4
;
}5 = }
25
4
}9
0,405
d) 1,0
4
}7
h)
2
}3
1,000
5
}6
b) Kürze die Brüche.
2
}7 = }
35
12
;
}
24
15
;
}
25
25
;
}
100
70
}
100
6. Berechne.
a) }23 + }45
b) }56 + }79 – }13
4
3 1
c) }
+}
–}
16 12 4
1
d) }35 – }
+ }3
10 4
7. Löse die Aufgabenketten. Was stellst du fest?
a) 8 · }14
4 · }14
2 · }14
1 · }14
}2 · }4
1 1
b) 4 : }12
2 : }12
1 : }12
}2 : }2
1 1
}4 : }2
1 1
8. Belege die Leerstelle mit einer Zahl, sodass richtig gelöste Aufgaben entstehen.
a)
+ 3 = 12
– 4 = 16
= 15
3·
:9 = 6
d) 4,5 ·
= 0,45
b) }45 + }5 = }75
4
1
}7 – }7 = }7
2
= }56
}3 +
7
19
=}
}4 + }
10 20
e) }25 ·
6
=}
10
c) 2,3 +
= 4,5
7,8 –
= 2,4
+ 1,5 = 6,1
1,3 –
f ) }45 :
= 1,03
4
=}
35
2,5 :
= 0,5
}9 · }7 = }
63
4
20
}7 : }5 = }
21
3,6 :
=3
}6 · } = }
12
5 2
5
:} = }
}
15 3 10
: 0,2 = 4
231262_NRW7_online_Aufgaben.indd1 1
8
2
·} = }
}
12 15 9
2
10
7
7
5
=1
}9 :
21.01.2008 8:23:57 Uhr
2 Rationale Zahlen
Rationale Zahlen
Positive und negative Zahlen
1. Zeichne eine Zahlengerade, die von –10 bis +10 reicht. Kennzeichne dort die Punkte, die zu
den folgenden Zahlen gehören:
A = –9,5;
B = + 8,25;
C = –7,1;
D = + 6,2;
E = – 5,4;
F = + 4,7
2. Setze das richtige Relationszeichen (<; =; >).
a) 0
3
b) – 3
–12
c) – 2
10
–}
15
g) |– 2,7|
e) – 0,9
–0,09
f ) – }46
i) |– 3|
|3|
j) }56
m) 17 + 11
17
| – }56 |
n) 15
15 – 15
1
d) 2
3
–1
h) 0,2
k) 5
– (–5)
l) – 4,4
o) 0
– 22 – 22
p) –15 · 2
|– 2,9|
– 4,44
–7 · 0
3. Trage die folgenden Punkte in ein Koordinatensystem und versuche, durch Verbinden der
Punkte eine Figur zu erkennen:
a) A1(–1 | 4); A2(– 2 | 0); A3(– 6 | –1); A4(– 2 | – 2); A5(–1 | – 6); A6(0 | – 2); A7(4 | –1); A8(0 | 0)
b) B1(5 | 5); B2(0 | 3); B3(– 5 | 5); B4(– 3 | 0); B5(– 5 | – 5); B6(0 | – 3); B7(5 | – 5); B8(3 | 0)
Addition und Subtraktion
Löse die Aufgaben.
1. a) (+ 37) + (+ 85)
d) (+ 63) + (+ 68)
g) (+ 95) + (+ 548)
b) (+ 73) + (+ 58)
e) (+ 29) + (+ 93)
h) (+ 88) + (+ 324)
c) (+ 46) + (+77)
f ) (+ 62) + (+ 217)
i) (+76) + (+ 639)
2. a) (+1,2) + (+7,8)
d) (+ 4,5) + (+ 2,6)
g) (+ 3,5) + (+ 37,49)
b) (+ 2,3) + (+ 8,9)
e) (+ 5,6) + (+ 6,5)
h) (+ 8,6) + (+ 65,52)
c) (+ 3,4) + (+ 9,3)
f ) (+ 2,3) + (+ 25,64)
i) (+7,8) + (+ 42,81)
3. a) (+ 23,7) + (+ 435,81)
d) (+ 62,8) + (+ 279,64)
g) (+ 23,46) + (+ 3,03)
b) (+72,3) + (+ 694,75)
e) (+ 35,4) + (+183,76)
h) (+ 890,3) + (+ 49,4)
c) (+ 85,6) + (+741,79)
f ) (+ 6,789) + (+ 21,2)
i) (+ 45,61) + (+ 5,85)
4. a) (– 43) + (–74)
d) (–79) + (– 96)
g) (– 26) + (– 275)
b) (– 55) + (– 69)
e) (– 81) + (– 48)
h) (–19) + (– 383)
c) (– 67) + (– 85)
f ) (– 39) + (–764)
i) (– 44) + (– 859)
5. a) (–123) + (– 676)
d) (–789) + (– 303)
g) (– 468) + (– 2 235)
b) (– 345) + (– 585)
e) (– 901) + (– 212)
h) (– 802) + (– 3 879)
c) (– 567) + (– 494)
f ) (– 246) + (– 4 657)
i) (– 246) + (– 5 465)
6. a) (–7,2) + (– 4,7)
d) (– 8,6) + (– 3,4)
g) (– 2,6) + (–78,95)
b) (– 6,4) + (– 5,8)
e) (– 2,4) + (–7,5)
h) (– 4,9) + (– 37,24)
c) (– 5,3) + (– 6,9)
f ) (–1,5) + (– 45,62)
i) (–7,8) + (– 54,19)
231262_NRW7_online_Aufgaben.indd2 2
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:23:58 Uhr
Rationale Zahlen 3
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
7. a) (– 32,6) + (– 224,42)
d) (– 61,7) + (– 368,63)
g) (– 4,679) + (– 616,9)
b) (– 67,8) + (–184,21)
e) (– 56,4) + (– 457,56)
h) (– 58,06) + (–7,097)
c) (– 49,2) + (– 974,94)
f ) (–132,4) + (– 52,38)
i) (–734,2) + (– 45,25)
8. a) (+ 67) + (– 87)
d) (– 83) + (+ 53)
g) (+ 54) + (– 94)
b) (– 38) + (+ 49)
e) (+ 92) + (– 49)
h) (– 45) + (+ 49)
c) (+76) + (– 35)
f ) (– 29) + (+12)
i) (+17) + (– 37)
9. a) (– 237) + (+175)
d) (+732) + (– 976)
g) (– 491) + (+ 281)
b) (+ 372) + (– 283)
e) (– 327) + (+273)
h) (+ 941) + (– 821)
c) (–723) + (+ 847)
f ) (+ 273) + (–128)
i) (–149) + (+182)
10. a) (+7,2) + (– 5,4)
d) (– 8,4) + (+ 8,1)
g) (+ 6,3) + (– 8,6)
b) (– 2,7) + (+ 4,5)
e) (+1,5) + (– 2,7)
h) (– 3,6) + (+ 6,8)
c) (+ 4,8) + (– 9,9)
f ) (– 5,1) + (+7,2)
i) (+ 9,2) + (– 8,7)
11. a) (– 35,2) + (+ 253,5)
d) (+ 52,3) + (– 352,9)
g) (–72,4) + (+ 427,8)
b) (+ 25,3) + (– 325,6)
e) (– 32,5) + (+ 532,6)
h) (+ 47,2) + (– 274,1)
c) (– 53,2) + (+ 253,1)
f ) (+ 23,5) + (– 532,6)
i) (– 24,7) + (+ 365,4)
12. a) (+27) – (+63)
d) (–48) – (+79)
g) (+61,2) – (+72,3)
b) (+72) – (–36)
e) (–12,6) – (+23,7)
h) (+40,17) – (–74,01)
c) (–84) – (–97)
f ) (–26,1) – (–37,2)
i) (– 34,7) – (+ 25,25)
13. a) (+ 496) – (– 337)
d) (+ 6 374) – (+ 3 746)
g) (+ 4 873) – (–1 239)
b) (+ 543) – (+ 489)
e) (– 3 456) – (– 4 563)
h) (– 4 083) – (+ 2 691)
c) (+ 5 834) – (– 337)
f ) (– 6 198) – (–1986)
i) (+ 5 724) – (– 3 167)
14. a) (+ 50,17) – (– 84,01)
d) (– 21,4) – (+ 37,9)
g) (+ 23,6) – (– 43,2)
b) (– 27,9) – (– 53,8)
e) (– 42,7) – (– 26,8)
h) (+72,3) – (–12,4)
c) (– 87,2) – (+12,6)
f ) (+ 48,6) – (+ 37,7)
i) (+ 63,1) – (+ 85,6)
15. a)
b)
c)
d)
92 – 94 – 65 + 72 + 87 – 49 – 37 – 26 + 52 – 56 + 66
– 81 + 84 – 53 + 12 – 75 + 34 – 73 – 47 + 67 – 68 – 88
–70 + 72 – 41 + 14 – 63 – 19 – 62 + 19 – 89 – 71 – 99
69 – 71 – 29 + 36 + 51 + 91 – 26 + 82 – 73 + 42 – 11
16. a)
b)
c)
d)
– 563 – 792 + 784 + 326 – 487 – 714 + 563 – 729 + 653 + 972
+ 279 – 478 – 632 + 748 + 471 – 356 – 279 – 487 + 729 – 784
– 847 + 263 + 874 – 147 – 635 + 927 – 847 – 236 + 487 – 632
326 + 487 – 714 – 563 + 792 + 784 + 326 – 478 + 236 – 874
Multiplikation
1. Berechne.
a) –1 · 0,5
b) – 0,5 · 4
c) – 4 · 0,3
d) –10 · 0,04
231262_NRW7_online_Aufgaben.indd3 3
– 2 · 0,6
– 2,5 · 6
–12 · 0,1
– 3 · 14
–7 · 0,3
– 2,1 · 9
2,4 · (– 2)
– 0,4 · 0,5
–10 · 1,2
–1,5 · 3
– 3,6 · 0
1,7 · (– 4)
– 5 · 0,4
–1,8 · 2
0,8 · (– 5)
–1,35 · 100
21.01.2008 8:23:58 Uhr
4 Rationale Zahlen
2. Berechne. Lege zuerst das Vorzeichen des Ergebnisses fest.
a) – 2 · (– 4)
–17 · (– 3)
– 6 · (– 8)
– 25 · (– 5)
b) –1,2 · (– 5)
– 4 · (– 4,1)
–11 · 1,1
– 3,2 · (– 3)
c) 4 · 7
12 · (– 3)
40 · (– 8)
– 23 · (– 2)
d) – 5 · (– 0,6)
0,6 · 0,7
– 6,5 · 3
–15 · (–10)
– 31 · (– 3)
– 0,01 · (–100)
–1 · (– 0,7)
– 65 · 0,01
3. Löse folgende Aufgaben. Bestimme zunächst das Vorzeichen des Produkts.
a) 3 · 5 · (– 4)
– 6 · (– 4) · 10
12 · 0,5 · (– 2)
–7 · (– 5) · (– 2)
–2 · (– 3) · (– 4) · (– 5)
b) – 4 · (– 3) · 6
–10 · (– 5) · 0,1
5 · 2 · 8 · (– 3) · (–1)
6 · 10 · (– 4) · (– 3)
2 · (–10) · (– 5) · (– 4)
c) – 5 · (– 4) · (– 3) · (–10)
5 · (–10) · 4 · 5 · (– 3)
30 · (– 0,5) · 6
–12 · (– 5) · (– 4)
4 · 8 · 3 · (– 2)
4. Bestimme x jeweils so, dass wahre Aussagen entstehen.
a) – 5 · x = 25
b) x · (–5) = 60
c) –10 · x = 15
12 · x = – 48
– 39 · x = 0
– 4 · x = 28
–9 · x = 81
x · 8 = – 48
– 30 · x = 15
d) 12 · x = 18
–32 · x = 64
–x · 12 = 36
5. Übertrage ins Heft und ergänze die Tabellen.
·
a)
–7
– 0,4
11
·
b)
3
– 0,25
–5
0,5
12
0,1
–10
6. Bestimme das Vorzeichen und rechne dann schriftlich. Führe eine Überschlagsrechnung
durch.
a) 8,5 · (– 4,2)
b) – 2 028 · (– 88)
c) 47,4 · (– 0,82)
d) – 2 546 · 8
e) 171,2 · (–18)
7. Übetrage die folgende Tabelle in dein Heft und löse die Aufgaben:
x
–7
+8
–11
–17
+13
– 0,7
+1,8
–7,2
+2,9
y
+9
–6
–13
+14
–16
+ 0,6
– 0,4
– 0,7
+1,1
x·y
(– x) · y
(– x) · (– y)
x · (– y)
– (x · y)
Division
1. Berechne.
a) – 6 : 3
b) 18 : (– 6)
c) 120 : (– 3)
231262_NRW7_online_Aufgaben.indd4 4
–12 : 6
9 : (– 9)
–1 000 : (– 50)
– 2 : 0,2
100 : (– 25)
– 3,8 : (– 2)
– 60 : 12
51 : (– 3)
–15 : (–1,5)
– 0,75 : 3
30 : (– 0,5)
– 99 : (–100)
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:23:59 Uhr
Rationale Zahlen
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
5
2. Bestimme zunächst das Vorzeichen und rechne dann schriftlich. Führe eine Überschlagsrechnung durch.
a) 1 230 : (–120)
b) – 2 028 : (–78)
c) 77,4 : (– 0,32)
d) – 526,5 : 22
e) 871,2 : (– 88)
f ) – 40,8 : (– 0,8)
3. Welches Vorzeichen hat das Ergebnis? Bestimme den Quotienten der Beträge beider Zahlen
durch schriftliches Rechnen.
a) –12 466 : (– 23)
b) 738,3 : (– 0,6)
c) 0,048 : (– 0,4)
d) 576 : (– 24)
e) 197,12 : (–12,8)
f ) – 30,82 : (–13,4)
g) – 837 : 31
h) – 4 144 : (–74)
4. Übernimm die Tabellen ins Heft und rechne.
a)
:
–6
12
–4
3
:
b)
84
72
– 0,36
– 0,18
144
216
–6
1,2
–9
5. Ermittle jeweils, für welches a eine wahre Aussage entsteht.
a) – 96 : a = –12
b) – 35 : a = 5
d) a : (–12) = 8
e) a : (– 4) = –15
c) a : (– 90) = 3
f ) 0,9 : (– a) = 0,3
6. Berechne.
a) –5 · (–21) : 7
d) (15 – 25) : 5
c) (7 – 12) : (– 8 + 3)
f ) (–72 – 48) : (– 4)
7. Berechne.
a) (+ 42) : (–7)
e) (– 96) : (+12)
i) (– 24,8) : (– 0,8)
( )( )
m) + }34 : – }12
b) 25 : (6,3 – 1,3)
e) (– 88 + 55) : 11
b) (+119) : (–17)
f ) (–108) : (–18)
j) (– 5,8) : (17,4)
( )( )
13
n) + }83 : – }
8
c) (–72) : (– 8)
g) (– 64) : (+16)
k) (+ 2,75) : (– 0,25)
18
d) (+ 92) : (+ 4)
h) (–105) : (+ 21)
l) (– 4,95) : (– 33)
( )( )
( )( )
19
20
o) – }
: –}
2
3
31
15
p) – }
: –}
6
4
8. Übernimm die Tabelle ins Heft und rechne.
x
a)
5,6
b)
– 56,6
x : 10
x : 100
231262_NRW7_online_Aufgaben.indd5 5
100 · x
100
c)
d)
10 · x
–3
21.01.2008 8:23:59 Uhr
6 Zuordnungen, Proportionalitäten
Zuordnungen, Proportionalitäten
1. Untersuche, ob zwischen den Zahlen für x und y eine proportionale oder antiproportionale
Zuordnung besteht und gib, wenn möglich, den Proportionalitätsfaktor an.
a) x
0,5
1,0
1,5
2,0
2,5
3,0
b) x
2
4
6
8
10
12
y
2,5
5,0
7,5
10,0
12,5
15,0
y
12
6
4
3
2,4
2
c) x
1
2
3
4
5
6
d) x
0,2
0,4
0,6
0,8
0,9
1,2
y
1
4
9
16
25
36
y
0,5
1,0
1,5
2,0
2,25
3,0
7
5
4
2,7
2. Ergänze so, dass eine proportionale Zuordnung entsteht.
a) a
2
b
6
4
4,8
15
72
120
b) s
t
13
5,2
1,95
3. Ergänze so, dass eine antiproportionale Zuordnung entsteht.
a) b
18
c
10
3
4
4
1,5
b) s
24
t
0,4
0,5
0,8
12
3
2
0,6
4. Berechne jeweils den Wert für x, wenn die Zuordnungen proportional sind.
a)
d)
Masse
Preis
b)
Anzahl
Preis
c)
Länge
Preis
4t
750 €
18 Stück
72 €
90 dm
54 €
16 t
x€
3 Stück
x€
x dm
18 €
Benzinmenge
Preis
Strecke
Zeit
Arbeitszeit
Lohn
2l
1,5 €
75 km
225 min
2h
56 €
38 l
x€
25 km
x min
66 h
x€
e)
f)
5. Berechne jeweils den Wert für x, wenn die Zuordnungen antiproportional sind.
a)
Arbeiter
Arbeitszeit
b) Baumaschinen
Arbeitszeit
c)
Anzahl der
Kühe
Futtervorrat
6 Arbeiter
13 h
4 Bagger
8h
2 Kühe
20 Tage
3 Arbeiter
xh
x Bagger
16 h
8 Kühe
x Tage
d) Personenzahl
Buspreis je
Person
e)
Arbeiter
Arbeitszeit
f)
Baumaschinen
Arbeitszeit
34 Personen
58 €
7 Arbeiter
8h
6 Bagger
20 h
x Personen
116 €
x Arbeiter
28 h
5 Bagger
xh
231262_NRW7_online_Aufgaben.indd6 6
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:24:00 Uhr
Zuordnungen, Proportionalitäten 7
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
6. Bei den folgenden Beispielen handelt es sich um proportionale Zusammenhänge.
Löse die Aufgaben. Erkläre dein Vorgehen.
a) 2 kg Äpfel kosten 4 €. Wie viel Euro kostet 1 kg Äpfel?
b) 6 Flaschen Mineralwasser kosten 2,40 €. Wie viel Euro kostet eine Flasche?
c) 10 Eier kosten 1,50 €. Wie viel Cent kostet ein Ei?
d) In 1,5 Stunden legt ein Radfahrer eine Strecke von 30 km zurück.
Wie viel Kilometer schafft er in einer Stunde?
e) Ein 4 m langer Holzbalken hat eine Masse von 42 kg.
Welche Masse hat ein entsprechender Balken von 1 m Länge?
f ) 800 g Schweinefleisch kosten 3,20 €. Wie viel Euro kosten 100 g Schweinefleisch?
g) Eine Seilbahn überwindet auf einer Strecke von 520 m einen Höhenunterschied von 260 m.
Auf welcher Strecke beträgt der Höhenunterschied 100 m?
h) 1 kg Tomaten kostet 1,35 €. Wie viel Euro kosten 2 kg Tomaten?
i) 1 Flasche Saft kostet 1,04 €. Wie viel Euro kosten 6 Flaschen?
j) Ein Ei kostet 9 Cent. Wie viel Euro kosten 12 Eier?
k) Ein Dampfer fährt in einer Stunde 30 km. Wie weit kommt er in 1,5 Stunden?
l) 1 m3 Holz wiegt 1,2 t. Wie schwer sind 4 m3 Holz?
m) Eine Straße steigt auf einer Länge von 100 m um 8 m.
Wie groß ist der Höhenunterschied bei einer Länge von 900 m?
n) 1 kg Rindfleisch kostet 6,46 €. Wie viel Euro kosten 500 g Rindfleisch?
7. Bei den folgenden Beispielen handelt es sich um antiproportionale Zusammenhänge.
Löse die Aufgaben. Erkläre dein Vorgehen.
a) 2 Arbeiter brauchen für eine bestimmte Arbeit 3 Stunden.
Wie lange braucht ein Arbeiter für die gleiche Arbeit?
b) 2 gleich starke Pumpen füllen ein Schwimmbecken in 7 Stunden.
Wie lange braucht eine Pumpe dafür?
c) Wenn sich 4 Personen den Preis für eine Taxifahrt teilen, muss jeder 7,05 € bezahlen.
Wie viel Euro muss eine Person allein bezahlen?
d) Wenn man eine Klasse in Dreiergruppen teilt, entstehen 8 Gruppen.
Wie groß ist die gesamte Klasse?
e) Wenn Gerd 5 € pro Tag ausgibt, reicht sein Urlaubsgeld 4 Tage.
Wie lange reicht es, wenn er 1 € pro Tag ausgibt?
f ) Wenn Frau Krause es schafft, in jeder Woche 800 g abzunehmen, hat sie ihr Idealgewicht in
6 Wochen erreicht.
Wie lange dauert es, wenn sie 400 g pro Woche abnimmt?
km
braucht man mit dem Auto bis zum Bahnhof 10 min.
g) Bei einer Geschwindigkeit von 50 }
h
km
?
Wie lange braucht man dafür bei einer Geschwindigkeit von 10 }
h
h) Ein Maler braucht zum Streichen eines Zauns 9 Stunden.
Wie lange brauchen 3 Maler für die gleiche Arbeit bei gleichem Tempo?
i) Eine Pumpe pumpt ein Becken in 7 Stunden leer. Wie lange brauchen 2 Pumpen?
j) Eine Klasse besteht aus 24 Schülern.
Wie viele Möglichkeiten gibt es, sie in Gruppen gleicher Größe einzuteilen?
k) Wenn sich Gerd jeden Tag ein Softeis kauft, reicht sein Taschengeld 30 Tage.
Wie lange reicht es, wenn er jeden Tag drei Softeis kauft?
231262_NRW7_online_Aufgaben.indd7 7
21.01.2008 8:24:00 Uhr
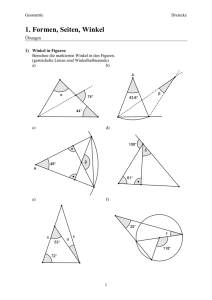
8 Winkel
Winkel
Wenn Geraden einander schneiden
1. Berechne die Winkelgrößen von α; β und γ. Begründe.
a)
b)
124°
γ
α
β
β
c)
α
α
58°
43°
β
γ
2. Berechne jeweils, wie groß die gekennzeichneten Winkel sind.
a)
b)
γ2
γ
α
1
β2 20°
β1
24°
β
α1
c)
d)
α
γ1
96°
135°
γ1
86°
120°
β
γ
γ
ε
δ
α1
60°
β1
60°
α=β
3. Berechne die Größe aller gekennzeichneten Winkel.
a)
b)
°
α
68
42°
δ
ε
β
γ
45°
δ
c)
125° γ
α
231262_NRW7_online_Aufgaben.indd8 8
β
125°
70° δ
β γ
g
h
α
ε
ω
g|| h
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:24:01 Uhr
Winkel
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
9
Wenn Parallelen geschnitten werden
1. Berechne jeweils die fehlenden Winkelgrößen (g || h).
s
a)
α1
h
h
°
α2
g
b)
118
α3
55
α3
α5
α6
°
α1
α2
g
β2
β1
β3
β4
s
α4
α7
2. Berechne die gekennzeichneten Winkel. Begründe (g || h).
a)
b)
δ
ε
h
g
c)
114°
γ
β
α
β
h
γ
s
γ
s
ε
g
h
β
δ
45°
α
131°
α
g
s
3. Die nebenstehende (nicht maßstäbliche) Abbildung zeigt
ein Dreieck ABC und die Parallele zur Geraden AB durch
den Punkt C.
Ermittle die Größen von α; β und γ. Begründe.
67°
34°
γ
C
β
α
A
B
4. Berechne die gekennzeichneten Winkel für a || b und c || d.
Begründe die erhaltenen Ergebnisse.
a)
β
0°
15
b)
d
δ
γ
ε
γ
α
α
ε
c)
β
d
δ
δ
52°
c
60°
b
a
ε
c
α
β
a
b
a
5. Berechne jeweils die Größe aller Innenwinkel im Parallelogramm ABCD für folgende Werte.
Berechne jeweils auch die Summe dieser Winkel.
a) α = 58°
b) β = 90°
A
c) γ = 127°
231262_NRW7_online_Aufgaben.indd9 9
d
γ
b
D
C
γ
δ
α
c
β
B
21.01.2008 8:24:03 Uhr
10 Dreiecke
Dreiecke
Dreiecke unterscheiden
1. Vergleiche in jedem Dreieck die Länge der bezeichneten Seiten und die Größe der beiden gegenüberliegenden Winkel. Formuliere einen Zusammenhang.
a)
b)
a
γ
a
b
b
α
c)
γ
β
β
α
c
c
2. Von einem Dreieck ABC sind jeweils zwei Seitenlängen bekannt.
a) a = 7 cm
b) b = 12 cm
c) a = 4,1 cm
b = 5 cm
c = 15 cm
c = 6,3 cm
Vergleiche jeweils die Größe der gegenüberliegenden Innenwinkel.
d) b = 3,5 cm
c = 3,5 cm
3. Vom Dreieck ABC sind jeweils zwei Innenwinkelgrößen bekannt.
a) α = 64°
b) γ = 17°
c) β = 102°
β = 39°
α = 65°
γ = 29°
Vergleiche jeweils die Längen der gegenüberliegenden Seiten.
d) α = 45°
γ = 45°
4. Gibt es Dreiecke ABC mit folgenden Seitenlängen? Begründe mithilfe der Dreiecksungleichung. Gib gegebenenfalls die dritte Seite so an, dass es gebildet werden kann.
a) a = 5 cm
b) a = 2 cm
c) a = 7 cm
d) a = 28 cm
b = 4 cm
b = 6 cm
b = 6 cm
b = 65 cm
c = 3 cm
c = 9 cm
c = 1 cm
c = 38 cm
5. Begründe, warum es keine Dreiecke ABC mit folgenden Stücken gibt.
a) a = 4 cm
b) a = 5 cm
c) b = 7,5 cm
b = 2 cm
b = 2 cm
c = 2,2 cm
α = 70°
c = 3 cm
β = 35°
β = 80°
γ = 60°
d) a = 7,1 cm
b = 2,6 cm
c = 2,8 cm
6. In einem gleichschenkligen Dreieck ABC sind die Seiten a und b jeweils 5 cm lang. Welche
Länge könnte die Seite c haben? Begründe.
7. Es gilt folgender Satz: Die kürzeste Seite in einem Dreieck liegt stets einem spitzen Winkel gegenüber. Begründe diese Aussage.
Bilde die Umkehrung des Satzes. Ist die Umkehrung wahr oder falsch? Begründe.
8. Kerstin und Annett sitzen auf einer Bank
im Park. Für den Weg zur Bushaltestelle
schlägt Kerstin den Weg A vor. Annett hält
jedoch den Weg B für kürzer und möchte
diesen benutzen.
Für welchen Weg würdest du dich entscheiden? Begründe.
231262_NRW7_online_Aufgaben.indd10 10
B
A
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:24:04 Uhr
Dreiecke 11
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Dreiecke konstruieren und berechnen
1. Von einem gleichschenkligen Dreieck ABC ist bekannt:
a) Ein Basiswinkel ist 75° groß.
b) Der Winkel an der Spitze hat eine Größe von 102°.
c) Die Winkel α und β sind jeweils 63° groß, im Dreieck gibt
es Seitenlängen von 7,2 cm und 7,9 cm.
d) Der Winkel an der Spitze ist 48° groß, die kürzeste Seite
ist 5,2 cm lang.
Schreibe jeweils die Größen aller Seiten und Winkel auf, die
du aufgrund dieser Aussagen berechnen kannst.
C
a=b
γ
b
a
β
α
A
c
B
2. Gib jeweils die Größe jedes Innenwinkels an. Berechne alle eingezeichneten Winkel.
a)
b)
47°
α1
α
68°
A
α1
C
γ
α
74°
c)
γ1
β 60°
AB = BC
40°
B
3. Im Dreieck ABC gilt für die Innenwinkel:
a) β = 110°, α ist um 20° größer als γ .
b) γ = 60°, α ist halb so groß wie β.
c) α ist doppelt so groß wie β und γ ist dreimal so groß wie β.
Gib jeweils die Größe jedes Innenwinkels an.
55°
α
C
γ
A
α
β
B
4. Von einem Dreieck sind die Größen zweier Winkel gegeben.
Ordne die Seiten des Dreiecks der Länge nach. Beginne mit der längsten Seite.
a) α = 60° und γ = 52°
b) β = 67° und γ = 72°
c) α = 34° und β = 92°
d) β = 107° und γ = 36°
5. Berechne jeweils den Flächeninhalt und den Umfang des Dreiecks ABC.
a) a = 3 cm
b) a = 13 cm
c) a = 33 m
d)
b = 5 cm
b = 5 cm
b = 107 m
c = 4 cm
c = 12 cm
c = 112 m
β = 90°
α = 90°
γ = 90°
a
b
c
α
= 9,7 dm
= 900 mm
= 36 cm
= 90°
6. Wie ändert sich der Flächeninhalt eines Dreiecks bei folgenden Veränderungen?
a) Die Grundseite und die dazugehörige Höhe werden beide verdoppelt.
b) Die Grundseite wird verdoppelt und die dazugehörige Höhe bleibt gleich.
c) Die Grundseite und die dazugehörige Höhe werden beide halbiert.
231262_NRW7_online_Aufgaben.indd11 11
21.01.2008 8:24:05 Uhr
12 Terme
Terme
1. Übertrage die Tabelle in dein Heft und berechne die Werte der verschiedenen Terme.
Setze dabei für die Variablen die angegebenen Zahlen ein.
–4
–2
–1,6
–1
0
1
2
5
a) 3x + 1
b) – 2y – 4
c) 1,5 (a + 2)
d) d · d – 1
e) 2,4 – 4 · s
f ) – w + 2w
2. Gib für die folgenden Sachverhalte eine mathematische Formulierung mithilfe von Variablen
an:
a) das Dreifache einer beliebigen Zahl
b) das Doppelte einer beliebigen Zahl vermehrt um 7
c) der fünfte Teil einer beliebigen Zahl
d) das Achtfache einer beliebigen Zahl
e) die Differenz zweier verschiedener beliebiger Zahlen
f ) der Quotient aus 9 und dem um 3 verminderten fünften Teil der Zahl a
g) die Summe aus einer beliebigen Zahl und 9 ist gleich 17
h) das Produkt aus der Summe des Vierfachen der Zahl x und 3 und der Hälfte einer anderen
Zahl y
i) das Fünffache einer beliebigen Zahl
j) der dritte Teil einer Zahl a vermindert um 7
k) das Quadrat einer Zahl b geteilt durch 5
3. Berechne jeweils den Wert des Terms.
a) 3x – 2
für x = 4
c) 3(s – 4,2)
für s = 8,2
e) –2(4z + 4)
für z = –9
b) – 4a + 5
d) r : 6 – 3
f ) –1,2 (3y + 1)
4. Welchen Wert bekommen die Terme für a = – 2?
a) a + 15
b) a
c) 3 · a – 5
e) |a|
f ) |a + 2|
g)
a
}a + a
für a = 1,2
für r = 24
für y = 4
d) a – 2 · a
h) 3 · a – 2 · a
5. Setze für die Variablen eine Zahl so ein, dass wahre Aussagen entstehen.
a) 7 · x = 49
b) 105 : y = 21
c) 8 – 2z = 2
d) (56 + 8) : u = – 2
e) a · a – 8 = 17
f ) – 3w + 8 = 48 : 12
g) 6t – 4 = 20 – 2t
h) 4 (0,5s + 2) = 10
231262_NRW7_online_Aufgaben.indd12 12
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:24:06 Uhr
Terme 13
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
6. Fasse möglichst weit zusammen.
a) 2x + 3x
b) a + a + a + a
d) a + a + a + b + b + b + b
e) 20k – 4r + 5r – 21k
g) 2ab + 4ab – 12ab
h) 5k + 12k – 2k + 15k
7. Fasse zusammen.
a) 3x + 4x
e) – 96d + 9d
i) 2c – 3c + 9c
b) 11s + 3s + 52s
f ) 3,5f + 5,7f
c) 12e – 11e
g) 24k – 49k
d) 0,5a – 3,2a
h) – 5,1x – 2,8x + 3x
j) –7,4y + 0,5y
k) –17j – 25j
l) }14 y – }12 y
8. Fasse zusammen. Achte dabei auf die „nicht sichtbare Eins“.
a) 8m – m
b) – a + 89a
c) 23p + 7p +3p
e) b – 65b
f ) 5d + d – 7d
g) – 3n + n – n
9. Fasse zusammen.
a) 25a – 7b + 14a + 73b
d) –12s + 13 + 25s – 36s
g) 41e + 45 – 29e – 26 + 12e
b) 27g + d – 12d – 45g + d
e) 6,5 v – 8,9 v – 0,4u – 8,4u
h) 3,2x + 9,2 – 3x – 17 + 4y
10. Bestimme die Lösungsmenge.
a) 6x = 24
b) 8x = – 40
e) – 3x = – 30
c) s + s + s + 3 + 3 + 3
f ) 4 + 4x + 4y
i) (– 4) + (– 4x) + (– 4y)
f)
– 4 = }3y
d) 0,7x – x
h) w + w + 3w
c) 33x + 13y – 67x + x
f ) – 5u + 8t + 3u – 2u + 9t
i) 23r – 2t – 8r + t + t
c) }6x = 12
d) 120 = 5x
g) – 4,2 = 2a
h) 5b = 6
11. Löse folgende Gleichungen durch Anwenden der Umformungsregeln.
Gib die Lösungsmenge an. Führe eine Probe durch.
a) 10x – 6 = 14
b) 2x + 8 = 28
c) 11x + 22 = 33
d) 15 + 3x = 45
e) –15 + 4x = 1
f ) 3a – 1 = 53
g) 12 + }3y = 10
h) 18 = 7y – 31
i) 11 = 2x + 11
j) – 4x – 2 = –14
k) 13 + 2a – 15 = 0
l) 1,5x – 6 = –9
12. Ermittle diejenige rationale Zahl, die die Gleichung erfüllt.
Fasse dazu, wenn möglich, entsprechende Terme zuerst zusammen. Führe eine Probe durch.
a) 5x + 4 – 2x = 2x + 5
b) 12x – 6x – 10 = 4x – 6 – 2x
c) x + 7 + x + 8 = 12 – 3x – 7
d) 16 – a = 7a – 6a + 10
e) 10y – 3 – 5y + 8 = 15
f ) 22 = –5b + 6 + 3b + 8
g) 26z + 9 + 11 – 17z = –16 + 9
h) – x + 15 – 3x + 6 = –7x – 4x
13. Bestimme die Lösungsmenge. Kontrolliere deine Lösungen. Beachte die Grundmenge.
a) 12x – 5 + 3x – 4x + 8 – 3x + 5 – 7x = 23 – 2x
G=Q
b) –9 + 3y – 7y + 17 – 6 + 2y = 14 – 7y + 8 – 2y – 6
G=N
c) – 5a + 6 – 13a + 4 + 8a – 10 = 5a – 20 – 3a + 6a – 10
G=Q
d) 8d + 4,5 = 17d + 7,3 – 8d – 5d + 3,2 + 3d
G=Z
e) – 5 + 7x – 8 – 6x – 2x + 12 + 8x + 7 – 6 – 7x = 0
G=Q
14. Löse folgende Gleichungen:
a) x + 6 = 11
d) 12 = 6 + x
g) – 4 + b = –16
231262_NRW7_online_Aufgaben.indd13 13
b) x – 7 = 15
e) – 5 + x = – 23
h) 15,8 = z – 3,6
c) 19 + x = – 6
f ) a – 3,1 = 5,4
i) – 24,8 = 12,1 + y
21.01.2008 8:24:06 Uhr
14 Prozentrechnung
Prozentrechnung
Prozentwerte
1. Gib von den folgenden Schülerzahlen 2 % an:
a) 700
b) 300
c) 50
d) 450
g) 30
h) 70
i) 350
j) 620
e) 1 000
k) 7 850
2. Berechne von 600 km die gegebenen Anteile.
a) 2 %
b) 12 %
c) 112 %
f ) 140 %
g) 4 %
h) 40 %
3. Berechne.
a) 45 % von 720
d) 250 % von 189,54
g) 2,2 % von 1 200
d) 1,2 %
i) 400 %
b) 75 % von 324
e) 47,3 % von 85
h) 5 % von 528
f ) 1 100
l) 26 300
e) 120 %
j) 0,4 %
c) 24,3 % von 780
f ) 40 % von 1 800
i) 6 % von 440
4. Berechne und vergleiche die Ergebnisse der folgenden Aufgaben:
a) 20 % von 300
b) 19 % von 310
c) 18 % von 320
d) 17 % von 330
e) 16 % von 340
f ) 15 % von 350
5. Vergleiche. Setze das richtige Zeichen (<; =; >).
a) 27 % von 520 und 25 % von 560
b) 220 % von 36 und 36 % von 220
c) 16,6 % von 72 und 12,5 % von 96
d) 1,7 % von 350 und 17 % von 35
Prozentsätze
1. Wie viel Prozent von 400 km entsprechen folgende Längenangaben?
a) 80 km
b) 120 km
c) 600 km
d) 48 km
e) 170 km
f ) 1 km
2. Wie viel Prozent sind 15 m von den folgenden Längenangaben?
a) 150 m
b) 30 m
c) 7,5 m
d) 45 m
e) 3 000 m
f) 1 m
3. Wie viel Prozent sind
a) 16 von 32;
b) 7 von 140;
e) 112 von 70;
f ) 26 von 650;
4. Berechne jeweils den Prozentsatz.
a) 619,2 m von 1 720 m
c) 72,4 t von 181 t
5. Gib in Prozent an.
a) 1 g von 1 kg
d) 1 min von 1 h
c) 23 von 11,5;
d) 2,8 von 84;
g) 27 von 72;
h) }14 von 0,5?
b) 17,29 g von 45,5 g
d) 3 150 m von 7 500 m
b) 1 ha von 1 km2
e) 1 h von 1 Tag
c) 1 mm von 1 cm
f ) 1 Tag von 1 Jahr
6. Berechne die Prozentsätze. Runde das Ergebnis auf eine Dezimalstelle.
a) 4,7 von 13,5
b) 812 von 852
c) 62,5 von 170,3
d) 0,62 von 31
e) 572 von 275
f ) 83,6 von 120
g) 49 von 243
h) 39,5 von 164
i) 123 von 32,1
231262_NRW7_online_Aufgaben.indd14 14
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:24:06 Uhr
Prozentrechnung 15
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Grundwerte
1. Die folgenden Figuren sind jeweils Teil einer Gesamtfigur. Wie könnte diese aussehen?
a)
b)
c)
75%
25%
60%
2. Gib jeweils an, wie viel 100 % sind.
a) 10 % sind 18 kg
b) 50 % sind 18 kg
d) 60 % sind 18 kg
c) 200 % sind 18 kg
f ) 33 }13 % sind 18 kg
e) 0,5 % sind 18 kg
3. Gib jeweils den Grundwert an.
a) 18 t sind 80 %
b) 162 t sind 80 %
d) 36 t sind 72 %
e) 5,6 t sind 72 %
c) 1 t sind 80 %
f ) 56 t sind 72 %
4. Berechne jeweils 100 %. Runde die Ergebnisse auf Ganze.
a) 75,9 % sind 4 500 cm
b) 3,7 % sind 225 cm
d) 105 % sind 7 400 cm
e) 0,3 % sind 21,50 cm
c) 18,6 % sind 1 212 cm
f ) 16 % sind 1 280 cm
Prozentuale Veränderungen
1. Vermehre die folgenden Größenangaben jeweils um 12 % bzw. auf 122 %.
a) 200 m
b) 120 dt
c) 48 g
d) 9,6 cm2
e) 15,30 km
2. Vermindere die folgenden Größenangaben jeweils um 12 % bzw. auf 78 %.
a) 400 m
b) 240 dt
c) 96 g
d) 19,2 m2
e) 30,60 km
3. Vermehre.
a) 150 um 10 %
b) 8 800 auf 112 %
c) 84 um 45 %
d) 3 440 auf 149 %
4. Die folgenden Preise werden um 15 % gesenkt. Wie viel Euro kosten die Waren dann?
a) 30,00 €
b) 16,00 €
c) 51,00 €
d) 17,50 €
e) 199,90 €
f ) 999,00 €
5. Die folgenden Angaben sind Preise nach einer Preissenkung um 15 %. Wie viel Euro kosteten
die Waren vor der Preissenkung?
a) 30,00 €
b) 16,00 €
c) 51,00 €
d) 17,50 €
e) 199,90 €
f ) 999,00 €
6. Auf Waren wird eine Mehrwertsteuer von 19 % bzw. 7 % des Grundbetrags erhoben. Berechne
die jeweiligen Mehrwertsteuern in Euro und den Preis (Grundbetrag + Mehrwertsteuer).
a) 30,00 €
b) 275 €
c) 1 900,00 €
d) 0,54 €
e) 128,50 €
f ) 250 000 €
7. Auf wie viel Prozent (um wie viel Prozent) wurden die Zahlen verkleinert?
a)
b)
c)
d)
e)
f)
ursprüngliche Zahl
200
340
428
27
37
1 290
verkleinerte Zahl
180
172
321
25
35
1 285
231262_NRW7_online_Aufgaben.indd15 15
21.01.2008 8:24:07 Uhr
16 Knobelei
Knobelei
1. Kreuzzahlrätsel
waagerecht: a 79 · 4
f 23 · 33
i 136 · 4
o 23 · 40
senkrecht:
c
g
n
p
a
72 – 24
e 8,5 · 8
320 : 4
h 28 – 14
20 + 30 + 35
6·4·4
b
e
f
g
h
i
a 450 – 42 – 40
b 700 + 605 + 500
c 103,5 · 4
d 200 – 114
f 4 280 : 20 k 180 + 290 l 16 · 16
m 25 · 8 – 101
n 147 – 58
c
k
d
l
m
n
o
p
2. Wenn du von einer rationalen Zahl 10 subtrahierst, die Differenz verdoppelst und dann 10 addierst, dieses Ergebnis halbierst und nun noch 5 dazu rechnest, so erhälst du deine ursprüngliche wieder. Prüfe die Aussage mit der Zahl – 20 nach.
3. Hier stimmt was nicht? Lege jeweils nur ein Hölzchen um, so erhältst du wahre Aussagen.
a)
b)
c)
d)
4. Alexander behauptet, dass er Gedanken lesen kann. Er lässt Daniela folgende Rechnung ausführen:
„Denke dir eine natürliche Zahl, multipliziere ihren Nachfolger mit 5, vermindere dieses Ergebnis um 1 und subtrahiere deine gedachte Zahl. Dividiere nun durch 4 und nenne mir das
Ergebnis deiner Rechnung.“
Als Daniela ihm die Zahl 10 nennt, sagt er ihr die gedachte Zahl. Wie heißt diese?
5. Hinter einer der Türen liegt ein Goldschatz, hinter den anderen lauert das Verderben. Welche
musst du öffnen, um an den Schatz zu gelangen? Ich gebe dir eine Hilfe. Viel Glück.
Rätsel:
2 · T = }12 T+ 6
1
2
3
4
5
6
T ([ – 5) = [ · (T – 4)
6·M – 2 = [·M – 1
M Öffne.
6. Robert und Steffen spielen Zahlenraten. Robert: „Denke dir eine Zahl, addiere 4. Verdopple
die Summe und addiere zu ihr die gedachte Zahl. Von dem Ergebnis subtrahiere 8.“
Als Steffen das Ergebnis 39 nennt, weiß Robert, dass er sich die 13 gedacht hat. Erkläre, wieso
er das weiß.
7. Der Empfangschef des Hotels sagt: „Wir können 25 % der Gruppe bei uns unterbringen.“ Antwortet der Reiseleiter: „Prima, dann können ja alle hierbleiben, wir sind nur 24.“
Hat der Reiseleiter recht?
231262_NRW7_online_Aufgaben.indd16 16
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:24:09 Uhr
Rationale Zahlen 17
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Lösungen
Fit in Mathe
1. a)
c)
e)
i)
(75 + 25) + (16 + 84) = 200
4 · 25 · 21 = 2 100
0
f ) 8 · 40 = 320
270 : 9 – 54 : 9 = 24 j) 4 · 5 · 21 = 420
b) (87 – 17) + (21 + 39) = 130
d) 15 : 5 · 17 = 51
g) 28 : 4 = 7
h) 84 : 12 = 7
k) –162
l) 18 · 100 = 1 800
2. a) 10,8
g) 48,5
b) 0,374
h) 485
c) 0,4
i) 37,1
d) 3,8
j) 1,64
e) 1,8
k) 0,164
f ) 1,5
l) 0,025
3. a) }12
1
b) }
10
c) }13
d) }34
3
e) }
10
7
f) }
24
4. a) <
e) >
5. a) }69 ;
b) >
c)
>
d) =
f)
g) <
h) <
<
20
10
; }
}
25
35
7
b) }12 ; }35 ; }14 ; }
10
22
7
6. a) }
= 1}
15
15
23
5
b) }
= 1}
18
18
7. a) 2; 1; }12 ; }14 ; }18
b) 8; 4; 2; 1;
c) }14
25 5
d) }
= } = 1 }14
20 4
Halbieren eines Faktors führt zum Halbieren des Produkts.
1
}2
Halbieren des Dividenden führt zum Verdoppeln des Quotienten.
8. a) 9 + 3 = 12
20 – 4 = 16
3 · 5 = 15
54 : 9 = 6
4
2
b) }45 + }35 = }75
}7 – }7 = }7
3
1
}3 + }6 = }6
1
5
=}
}4 + }
10 20
1
c) 2,3 + 2,2 = 4,5
7,8 – 5,4 = 2,4
4,6 + 1,5 = 6,1
1,3 – 0,27 = 1,03
d) 4,5 · 0,1 = 0,45
2,5 : 5 = 0,5
3,6 : 1,2 = 3
0,8 : 0,2 = 4
6
e) }25 · }32 = }
10
}9 · }7 = }
63
4 5
20
}6 · }4 = }
12
5 2
·} = }
}
12 15 9
4
f ) }45 : 7 = }
35
}7 : }5 = }
21
2 3
10
:} = }
}
15 3 10
7 2
}9 : }9 = 1
5
5
7
7
8
19
2
5 5
Rationale Zahlen
Positive und negative Zahlen
1. individuelle Lösung
2. a) <
b) >
c) <
d) >
e) <
f)
=
g) <
h) <
i)
j)
=
k) =
l)
n) >
o) >
p) <
=
m) >
3. a) Stern
231262_NRW7_online_Loesungen.ind17 17
>
b) Stern
21.01.2008 8:53:31 Uhr
18 Rationale Zahlen
Addition und Subtraktion
1. a) +122
f ) + 279
b) +131
g) + 643
c) +123
h) + 412
d) +131
i) +715
e) +122
2. a) + 9,0
f ) + 27,94
b) +11,2
g) + 40,99
c) +12,7
h) +74,12
d) +7,1
i) + 50,61
e) +12,1
3. a) + 459,51
f ) + 27,989
b) +767,05
g) + 26,49
c) + 827,39
h) + 939,7
d) + 342,44
i) + 51,46
e) + 219,16
4. a) –117
f ) – 803
b) –124
g) – 301
c) –152
h) – 402
d) –175
i) – 903
e) –129
5. a) –799
f ) – 4 903
b) – 930
g) – 2 703
c) –1 061
h) – 4 681
d) –1 092
i) – 5 711
e) –1 113
6. a) –11,9
f ) – 47,12
b) –12,2
g) – 81,55
c) –12,2
h) – 42,14
d) –12,0
i) – 61,99
e) – 9,9
7. a) – 257,02
f ) –184,78
b) – 252,01
g) – 621,579
c) –1 024,14
h) – 65,157
d) – 430,33
i) – 779,45
e) – 513,96
8. a) – 20
f ) –17
b) +11
g) – 40
c) +41
h) + 4
d) – 30
i) – 20
e) + 43
9. a) – 62
f ) +145
b) + 89
g) – 210
c) +124
h) +120
d) – 244
i) + 33
e) – 54
10. a) +1,8
f ) + 2,1
b) +1,8
g) – 2,3
c) – 5,1
h) + 3,2
d) – 0,3
i) + 0,5
e) –1,2
11. a) + 218,3
f ) – 509,1
b) – 300,3
g) + 355,4
c) +199,9
h) – 226,9
d) – 300,6
i) + 340,7
e) + 500,1
12. a) – 36
f ) +11,1
b) +108
g) –11,1
c) +13
h) 114,18
d) –127
i) – 59,95
e) – 36,3
13. a) + 833
f ) – 4 212
b) + 54
g) + 6 112
c) + 6 171
h) – 6 774
d) + 2 628
i) + 8 891
e) +1 107
14. a) +134,18
f ) +10,9
b) + 25,9
g) + 66,8
c) – 99,8
h) + 84,7
d) – 59,3
i) – 22,5
e) –15,9
15. a) + 42
b) – 288
c) – 409
d) +161
16. a) +13
b) –789
c) –793
d) + 322
–1,2
–15
–1,2
– 42
– 2,1
–18,9
– 4,8
– 0,2
–12
– 4,5
0
– 6,8
Multiplikation
1. a)
b)
c)
d)
– 0,5
–2
–1,2
– 0,4
231262_NRW7_online_Loesungen.ind18 18
–2
– 3,6
–4
–135
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:53:32 Uhr
Rationale Zahlen 19
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
2. a)
b)
c)
d)
+8
+6
+ 28
+3
+ 51
+16,4
– 36
+ 0,42
+ 48
–12,1
– 320
–19,5
+125
+ 9,6
+ 46
+150
+ 93
+1
+ 0,7
– 0,65
3. a) – 60
b) +72
c) + 600
+ 240
+5
+ 3 000
–12
+ 240
– 90
–70
+720
– 240
+ 120
– 400
–192
4. a) x = – 5
x = –4
x = –9
b) x = –12
x=0
x = –6
5. a)
c) x = –1,5
x = –7
x = – 0,5
·
–7
– 0,4
11
3
– 21
–1,2
–5
35
2
6. a) – 35,7
d) x = 1,5
x = –2
x = –3
b)
·
12
0,1
–10
33
– 0,25
–3
– 0,025
2,5
– 55
0,5
6
0,05
–5
b) 178 464
c) – 38,868
d) – 20 368
e) – 3 081,6
7. x
–7
+8
–11
–17
+13
– 0,7
+1,8
–7,2
+2,9
y
+9
–6
–13
+14
–16
+ 0,6
– 0,4
– 0,7
+1,1
x·y
– 63
– 48
+143
– 238
– 208
– 0,42
– 0,72
+ 5,04
+ 3,19
(– x) · y
+ 63
+ 48
–143
+ 238
+ 208
+ 0,42
+ 0,72
– 5,04
– 3,19
(– x) · (– y)
– 63
– 48
+143
– 238
– 208
– 0,42
– 0,72
+ 5,04
+ 3,19
x · (– y)
+ 63
+ 48
–143
+ 238
+ 208
+ 0,42
+ 0,72
– 5,04
– 3,19
– (x · y)
+ 63
+ 48
–143
+ 238
+ 208
+ 0,42
+ 0,72
– 5,04
– 3,19
Division
1. a) – 2
b) – 3
c) – 40
–2
–1
20
2. a) –10,25
b) 26
3. a) + 542
e) –15,4
4. a)
–10
–4
1,9
c) – 241,875
b) –1 230,5
f ) + 2,3
___
d) – 23,9318
– 0,25
– 60
0,99
e) – 9,9
c) – 0,12
g) – 27
:
–6
12
–4
3
84
–14
7
–21
– 0,36
0,06
– 0,03
144
– 24
12
231262_NRW7_online_Loesungen.ind19 19
–5
–17
10
b)
f ) 51
d) – 24
h) + 56
:
–6
1,2
–9
18
28
72
–12
60
–8
4
0,09
– 0,12
– 0,18
0,03
– 0,15
0,02
– 0,01
– 36
48
216
– 36
180
– 24
12
21.01.2008 8:53:32 Uhr
20 Zuordnungen, Proportionalitäten
5. a) a = 8
b) a = –7
c) a = – 270
d) a = – 96
e) a = 60
f ) a = –3
6. a) 15
b) 5
c) 1
d) – 2
e) – 3
f ) 30
7. a) – 6
b) –7
c) + 9
d) + 23
e) – 8
f) +6
g) – 4
h) – 5
i) + 31
j) – }13
k) –11
l) + 0,15
m)
– }32
n)
8. zeilenweise:
64
25
–}
= –1 }
39
39
o)
57
17
+}
= +1 }
40
40
a) 5,6; 0,56; 0,056; 56; 560
c) 10; 1; 0,1; 100; 1 000
p)
62
17
+}
= +1 }
45
45
b) – 56,6; – 5,66; – 0,566; – 566; – 5 660
d) – 300; – 30; – 3; – 3 000; – 30 000
Zuordnungen, Proportionalitäten
1. a) Vermutung: y _x
y und x wachsen in gleicher Weise (Verdopplung von y führt zur Verdopplung von x)
x
2,5
5,0
=}=…=5
}y = }
0,5 1,0
b) Vermutung:
y = 5x k = 5 proportionale Zuordnung
1
y _}x
y und x wachsen in unterschiedliche Richtungen. Die Paare sind produktgleich.
x · y = 2 · 12 = 4 · 6 = … = 24
1
y _}x k = 24 antiproportionale Zuordnung
c) keine Proportionalität:
keine Quotientengleichheit, keine Produktgleichheit
d) y _ x
Quotientengleichheit k = 2,5; y = 2,5 · x proportionale Zuordnung
2. a) a
5
2
4
60
100
15
b) s
10
7
5
4
2,7
1,5
b
6
2,4
4,8
72
120
18
t
13
9,1
6,5
5,2
3,51
1,95
3. a) b
18
12
10
9
4
1,5
b) s
0,2
0,4
0,5
0,8
1,2
4
c
2
3
3,6
4
9
24
t
12
6
4,8
3
2
0,6
4. a) x = 750 € · 4 = 3 000 €
d) x = 1,5 € · 19 = 28,5 €
b) x = 72 € : 6 = 12 €
e) x = 225 € : 3 = 75 €
5. a) 6 · 13 h = 3 · x h
x = 26
c) 2 · 20 Tage = 8 · x Tage x = 5
x=2
e) 7 · 8 h = x · 28 h
6. a) 2,00 €
h) 2,70 €
b) 0,40 €
i) 6,24 €
231262_NRW7_online_Loesungen.ind20 20
c) 15 Cent
j) 1,08 €
c) x = 90 dm : 3 = 30 dm
f ) x = 56 € · 33 = 1 848 €
b) 4 · 8 h = x · 16 h
d) 34 · 58 € = x · 116 €
f ) 6 · 20 h = 5 · x h
d) 20 km
k) 45 km
e) 10,5 kg
l) 4,8 t
x=2
x = 17
x = 24
f ) 0,40 €
m) 72 m
g) 200 m
n) 3,23 €
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:53:33 Uhr
Winkel
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
7. a) 6 Stunden
f ) 12 Wochen
b) 14 Stunden
g) 50 min
c) 28,20 €
h) 3 Stunden
j) Anzahl der Gruppen
Anzahl der Schüler pro Gruppe
d) 24 Schüler
i) 3,5 Stunden
21
e) 20 Tage
2
3
4
6
8
12
12
8
6
4
3
2
k) 10 Tage, wenn er nichts anderes kauft.
Winkel
Wenn Geraden einander schneiden
1. a) α = γ = 56° (Nebenwinkel), β = 124° (Scheitelwinkel)
b) α = γ = 122° (Nebenwinkel), β = 58° (Scheitelwinkel)
c) α = 137° (Nebenwinkel), β = 43° (Scheitelwinkel)
2. a) α = 45°
β = 135°
γ = 45°
b) α1 = 156°
β1 = β2 = 60°
γ1 = γ2 = 84°
c) α = β = 47°
γ = e = 47°
δ = 86°
3. a) a = 55°
β = 125°
γ = 55°
δ = 90°
ε = 45°
b) α = 70°
β = 68°
γ = 70°
δ = 42°
c) α = 55°
β = 110°
γ = 70°
δ = 110°
d) α1 = 120°
β1 = 120°
γ = γ1 = 60°
ε = 90°
ω = 125° (Wechselwinkel zu 125°)
Wenn Parallelen geschnitten werden
1. a) α2 = α5 = α7 = 118°; α1 = α3 = α4 = α6 = 62°
b) α2 = β1 = β3 = 55°; α1 = α3 = β2 = β4 = 125°
2. a) α = 45° (Scheitelwinkel)
β = 135° (Nebenw. zu γ)
γ = 45° (Stufenwinkel)
δ = 135° (Scheitelw. zu β)
ε = 45° (Wechselwinkel)
3. α = 34° (Stufenwinkel)
b) α = 66° (Nebenwinkel)
β = 114° (Scheitelwinkel)
γ = 114° (Stufenwinkel)
δ = 66° (Nebenw. zu γ)
ε = 114° (Scheitelw. zu γ)
β = 67° (Stufenwinkel)
c) α = 49° (Nebenwinkel)
β = 49° (Nebenw. zu γ)
γ = 131° (Wechselwinkel)
γ = 79° (180° – 67° – 34°)
4. a) α = 30° (Nebenwinkel)
b) α = 60° (Wechselwinkel)
c) α = 52° (Scheitelwinkel)
β = 150° (Stufenwinkel)
β = 120° (Nebenw. zu α)
β = 52° (Wechselw.zu α)
γ = 150° (Stufenwinkel zu β)
γ = 120° (Stufenw. zu β)
γ = 128° (Nebenw. zu δ)
δ = 30° (Nebenwinkel zu γ)
δ = 120° (Scheitelw. zu γ)
δ = 52° (Stufenw. zu β)
ε = 30° (Stufenwinkel zu δ)
ε = 120° (Stufenwinkel zu γ)
ε = 128° (Wechselw. zu γ)
5. a) γ = 58°; β = δ = 122 º
Innenwinkelsumme 360°
231262_NRW7_online_Loesungen.ind21 21
b) α = γ = δ = 90°
Innenwinkelsumme 360°
c) α = 127°; β = δ = 53°
Innenwinkelsumme 360°
21.01.2008 8:53:33 Uhr
22 Dreiecke
Dreiecke
Dreiecke unterscheiden
1. a) a > b; α > β
b) b > c; β > γ
c) c > a; γ > α
Der längeren von zwei Seiten liegt immer der größere Winkel gegenüber.
2. a) α > β
b) β < γ
c) α < γ
d) β = γ
3. a) a > b
b) c < a
c) b > c
d) a = c
4. a) ja, denn Dreiecksungleichung ist erfüllt
c) nein, denn b + c = a
b) nein, denn a + b < c
d) ja, denn Dreiecksungleichung ist erfüllt
5. a) a > b, aber α < β
c) b > c, aber β < γ
b) b + c = a
d) b + c < a
6. Die Seite c muss kürzer als 10 cm sein, da sonst die Dreiecksungleichung nicht erfüllt ist.
7. Die Innenwinkelsumme eines Dreiecks beträgt 180°. Demnach kann maximal ein Winkel im
Dreieck ein rechter Winkel oder ein stumpfer Winkel sein. Da die Größe des Winkels von der
Länge der gegenüberliegenden Seite abhängt, ist der der kürzesten Seite gegenüberliegende
Winkel immer kleiner als 90°.
Umkehrung:
Einem spitzen Winkel liegt stets die kürzeste Seite in einem Dreieck gegenüber.
Die Umkehrung ist falsch, da in einem Dreieck auch mehrere spitze Winkel existieren können.
Bei einem spitzwinkligen Dreieck beispielsweise sind alle drei Winkel spitze Winkel.
8. Annett hat recht wegen der Gültigkeit der Dreiecksungleichung.
Dreiecke konstruieren und berechnen
1. a)
b)
c)
d)
α = β = 75°; γ = 30°
γ = 102°; α = β = 39°
α = β = 63°; γ = 54°; a = b = 7,9 cm; c = 7,2 cm
γ = 48°; α = β = 66°; c = 5,2 cm
2. a) α = 65°
α1 = 115°
b) α = 53°; α1 = 127°
γ = 53°; γ1 = 127°
c) α = 65°
β = 25°
3. a) α = 45°; β = 110°; γ = 25°
b) α = 40°; β = 80°; γ = 60°
c) α = 60°; β = 30°; γ = 90°
4. a) b; a; c
b) c; b; a
c) b; c; a
d) b; a; c
5. a) u = 12 cm
A = 6 cm2
b) u = 30 dm
A = 30 dm2
c) u = 252 m
A = 1 765,5 m2
d) u = 22,3 dm
A = 16,2 dm2
6. a) Der Flächeninhalt vervierfacht sich.
b) Der Flächeninhalt verdoppelt sich.
c) Der Flächeninhalt wird geviertelt
231262_NRW7_online_Loesungen.ind22 22
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:53:34 Uhr
Terme 23
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Terme
1.
–4
–2
–1,6
–1
0
1
2
5
a) 3x + 1
–11
–5
– 3,8
–2
1
4
7
16
b) – 2y – 4
4
0
– 0,8
–2
–4
–6
–8
–14
c) 1,5 (a + 2)
–3
0
0,6
1,5
3
4,5
6
10,5
d) d · d – 1
15
3
1,56
0
–1
0
3
24
e) 2,4 – 4 · s
18,4
10,4
8,8
6,4
2,4
–1,6
– 5,6
–17,6
f ) – w + 2w
–4
–2
–1,6
–1
0
1
2
5
2. a) 3a
b) 2b + 7
e) e – f
f)
i) 5x
j)
3. a) 10
b) 0,2
4. a) 13
b) – 2
e) a = 5; – 5
g) – 25k
8. a) 7m
g) g + 9 = 17
h) (4x + 3) · }12 y
k) b2 : 5
d) 1
d) 2
e) 64
e) 2
f ) –15,6
f) 0
g) –1
h) – 2
c) z = 3
d) u = – 32
w = }43
g) t = 3
h) s = 1
b) 4a
g) – 6ab
c) 3s + 9
h) 30k
d) 3a + 4b
i) – 4 (1 + x + y)
e) –k + r
b) 66s
c) e
d) – 2,7a
e) – 87d
f ) 9,2f
h) – 4,9x
i) 8c
j) – 6,9y
k) – 42j
l) – }14 y
b) 88a
9. a) 39a + 66b
f ) – 4u + 17t
d) 8d
b) x = 5
f)
6. a) 5x
f ) 4 (1 + x + y)
c) c : 5
c) 12
c) –11
5. a) x = 7
7. a) 7x
g : ( }5a – 3)
a
}3 – 7
c) 33p
d) – 0,3x
b) –18g – 10d
g) 24e + 19
e) – 64b
f ) –d
c) – 33x + 13y
d) – 23s + 13
h) 0,2x + 4y – 7,8
g) – 3n
h) 5w
e) – 2,4v – 8,8u
i) 15r
10. a) L = {4}
e) L = {10}
b) L = {– 5}
f ) L = {–12}
c) L = {72}
g) L = {– 2,1}
d) L = {24}
h) L = {1,2}
11. a) L = {2}
e) L = {4}
i) L = {0}
b) L = {10}
f ) L = {18}
j) L = {3}
c) L = {1}
g) L = {– 6}
k) L = {1}
d) L = {10}
h) L = {7}
l) L = {– 2}
12. a) x = 1
e) y = 2
b) x = 1
f) b = –4
c) x = – 2
g) z = – 3
d) a = 3
h) x = – 3
13. a) L = {5}
b) L = {2}
c) L = { }; a = }35
d) L = {6}
e) L = Q
14. a) x = 5
f ) a = 8,5
b) x = 22
g) b = –12
c) x = – 25
h) z = 19,4
d) x = 6
i) y = – 36,9
e) x = –18
231262_NRW7_online_Loesungen.ind23 23
21.01.2008 8:53:34 Uhr
24 Prozentrechnung
Prozentrechnung
Prozentwerte
1. a) 14
g) 0,6
b) 6
h) 1,4
c) 1
i) 7
d) 9
j) 12,4
e) 20
k) 157
f ) 22
l) 526
2. a) 12 km
f ) 840 km
b) 72 km
g) 24 km
c) 672 km
h) 240 km
d) 7,20 km
i) 2 400 km
e) 720 km
j) 2,4 km
3. a) 324
f ) 720
b) 243
g) 26,4
c) 189,54
h) 26,4
d) 473,85
i) 26,4
e) 40,205
4. a) 60
b) 58,9
f ) < e) < d) < c) < b) < a)
5. a) 140,4 > 140
c) 57,6
b) 79,2 = 79,2
d) 56,1
e) 54,4
c) 11,95 < 12
f ) 52,5
d) 5,95 = 5,95
Prozentsätze
1. a) 20 %
b) 30 %
c) 150 %
d) 12 %
33 }31 %
3 }31 %
e) 42,5 %
f ) 0,25 %
e) 0,5 %
f ) 1 500 %
e) 160 %
f) 4%
2. a) 10 %
b) 50 %
c) 200 %
d)
3. a) 50 %
g) 37,5 %
b) 5 %
h) 50 %
c) 200 %
d)
4. a) 36 %
b) 38 %
c) 40 %
d) 42 %
5. a) 0,1 %
b) 1 %
c) 10 %
d) 1,6 %
e) 4,16 %
f ) 0,274 %
6. a) 34,8 %
g) 20,2 %
b) 95,3 %
h) 24,1 %
c) 36,7 %
i) 383,2 %
d) 2,0 %
e) 208,0 %
f ) 69,7 %
__
__
Grundwerte
1. a)
b)
Vorgabe
c)
Ergänzung zu 100%
2. a) 180 kg
b) 36 kg
c) 9 kg
d) 30 kg
e) 3 600 kg
f ) 54 kg
3. a) 22,5 t
b) 202,5 t
c) 1,25 t
d) 50 t
e) 7,8 t
f ) 77,8 t
4. a) 5 929 cm
d) 7 048 cm
231262_NRW7_online_Loesungen.ind24 24
b) 6 081 cm
e) 7 167 cm
c) 6 516 cm
f ) 8 000 cm
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
21.01.2008 8:53:36 Uhr
Knobelei 25
45
44
43
42
41
40
39
38
37
36
35
34
33
32
31
30
29
28
27
26
25
24
23
22
21
20
19
18
17
16
15
14
13
12
11
10
9
8
7
6
5
4
3
2
1
Prozentuale Veränderungen
1. + 12 %
+ 22 %
a) 224 m
a) 244 m
b) 134,4 dt
b) 146,4 dt
c) 53,76 g
c) 58,56 g
d) 10,752 cm2
d) 11,712 cm2
e) 17,136 km
e) 18,666 km
2. – 12 %
– 22 %
a) 352 m
a) 312 m
b) 211,2 dt
b) 187,2 dt
c) 84,48 g
c) 74,88 g
d) 16,896 cm2
d) 14,976 cm2
e) 26,928 km
e) 23,868 km
3. a) 165
b) 9 856
c) 121,8
d) 5 125,6
4. a) 25,50 €
b) 13,60 €
c) 43,35 €
d) 14,88 €
e) 169,92 €
f ) 849,15 €
5. a) 35,29 €
b) 18,82 €
c) 60,00 €
d) 20,59 €
e) 235,18 €
f ) 1 175,29 €
6.
a)
b)
c)
d)
e)
f)
7%
2,10 €
19,25 €
133 €
0,04 €
9€
17 500 €
G + 7%
32,10 €
294,25 €
2 033 €
0,58 €
137,50€
267 500 €
19 %
5,70 €
52,25 €
361 €
0,10 €
24,42 €
47 500 €
G + 19 %
35,70 €
327,25 €
2 261 €
0,64 €
152,92 €
297 500 €
a)
b)
c)
d)
e)
f)
auf wie viel Prozent
90 %
50,6 %
75 %
92,6 %
94,6 %
99,6 %
um wie viel Prozent
10 %
49,4 %
25 %
7,4 %
5,4 %
0,4 %
7.
Knobelei
1. waagerecht: a 316;
senkrecht: a 368;
c 48; e 68; f 216; g 80; h 14; i 544; n 85; o 920; p 96
b 1 805; c 414; d 86; f 214; k 470; l 256; m 99; n 89
2. [(– 20 – 10) · 2 + 10] : 2 + 5 = – 20
allgemein: [(a – 10) · 2 + 10] : 2 + 5 = a – 10 + 5 + 5 = a
3. a)
b)
4. gedachte Zahl: 9
allgemein: {[(n + 1) · 5] – 1 – n} : 4 = n + 1
5. T = 4
6. 2 (n + 4) + n – 8 = 3n
[=5
c)
d)
M=1
n – gedachte Zahl
1. Tür öffnen
Genannte Zahl durch 3 dividieren, um die gedachte Zahl (n) zu erhalten.
7. 25 % von 24 Personen sind 6 Personen; der Reiseleiter hat nicht recht.
231262_NRW7_online_Loesungen.ind25 25
21.01.2008 8:53:37 Uhr