B Bruchzahlen 1 Bruchteile und Anteile

Inhalt
A
Grundlagen
1
2
3
4
5
B
Bruchteile und Anteile
Bruchteile von Größen
Kürzen und Erweitern von Brüchen
Verhältnisse und Maßstäbe
Bruchzahlen
Positive rationale Zahlen
Dezimalschreibweise
Periodische Dezimalbrüche
Dezimalbrüche ordnen und runden
Addieren und Subtrahieren
Multiplizieren und Dividieren
Vermischte Rechnungen
Keine Angst vor Textaufgaben
27
29
30
31
32
34
35
Proportionale Zuordnungen – Prozentrechnung
1
2
3093_Buch.indb 4
20
22
23
24
25
26
Rechnen mit Dezimalbrüchen
1
2
3
4
5
6
7
E
12
14
16
17
18
19
Rechnen mit Brüchen
1
Addieren und Subtrahieren
2
Multiplizieren
3
Dividieren
4
Rechengesetze
5
Vermischte Übungen
Probe-Klassenarbeit: Bruchrechnen
D
6
7
8
10
11
Bruchteile – Brüche – Bruchzahlen
1
2
3
4
5
6
C
Die natürlichen Zahlen
Teilbarkeit natürlicher Zahlen
Rechnen mit natürlichen Zahlen
Umfänge und Flächeninhalte
Oberflächen und Rauminhalte
Zuordnungen
Proportionale Zuordnungen
36
38
13.07.2007 13:06:37
3
Dreisatzrechnung
4
Prozentrechnung
Probe-Klassenarbeit: Proportionalität und Prozente
F
Daten und Zufall
1
2
3
G
Häufigkeitstabellen und Diagramme
Kennwerte einer Häufigkeitsverteilung
Zufallsexperimente
Darstellungen – Modelle – Netze
Oberflächen und Volumen berechnen
65
67
Erweiterung des Zahlbereichs von N auf Z
Addieren und Subtrahieren
68
70
Terme und Gleichungen
1
2
3
Terme mit einer Variablen
Einfache Gleichungen
Äquivalenzumformungen
Lösungen
3093_Buch.indb 5
60
62
63
Ganze Zahlen
1
2
K
Achsenspiegelungen
Symmetrische Figuren
Grundkonstruktionen
Darstellungen und Berechnungen von Körpern
1
2
J
52
54
55
56
58
59
Achsenspiegelungen und Symmetrie
1
2
3
I
46
48
50
Ebene Geometrie
1
Grundlagen
2
Abstände
3
Ebenen und Winkel
4
Winkelmessung
5
Winkelarten
Probe-Klassenarbeit: Ebene Geometrie
H
41
42
45
72
74
75
76
13.07.2007 13:06:37
A Grundlagen
1
Die natürlichen Zahlen
Die natürlichen Zahlen fasst man zur Menge N zusammen:
N = {0, 1, 2, 3, 4, 5, 6, 7, ...}
Sie werden mithilfe der Kleiner-als-Beziehung der Größe nach geordnet
(0 < 1 < 2 < 3 < 4 < 5 < 6 < 7 < ...) und am Zahlenstrahl dargestellt.
0
1
2
3
4
5
6
7
8
9
10
0
10
20
30
40
50
60
70
80
90
100
0
100
200
300
400
500
600
700
800
900
1000
0
1000
2000
3000
4000
5000
6000
7000
8000
9000 10 000
Jede natürliche Zahl besitzt genau einen Nachfolger und bis auf die
Zahl 0 auch genau einen Vorgänger.
In der Regel schreiben wir die natürlichen Zahlen im Dezimalsystem
(Zehnersystem) und verwenden dabei die Stufenzahlen Einer (E),
Zehner (Z), Hunderter (H), Tausender (T) usw.
Sehr übersichtlich ist die Schreibweise in einer Stellenwerttafel.
B HMrd ZMrd Mrd HM ZM
M
HT
ZT
T
H
Z
E
1012 1011 1010 109 108 107 106 105 104 103 102 101
Die Stufenzahlen sind hier als Zehnerpotenzen geschrieben.
Beispiel 1 Lies die Zahl 4 609 630, gib Vorgänger und Nachfolger an, markiere ihre Stelle
auf einem Zahlenstrahl und runde sie auf Tausender (auf Millionen).
Lösung: Die Zahl heißt vier Millionen sechshundertneuntausendsechshundertdreißig, ihr Vorgänger ist 4 609 629, ihr Nachfolger 4 609 631.
4 600 000
4 650 00
4 700 000
Runden: 4 609 630 ≈ 4 610 000 (≈ 5 000 000).
Beispiel 2 Die kleinste mit sechs verschiedenen Ziffern geschriebene natürliche Zahl heißt
123 450, die größte 987 654.
6
3093_Buch.indb 6
13.07.2007 13:06:38
2 Teilbarkeit natürlicher Zahlen
2 Teilbarkeit natürlicher Zahlen
Ist eine natürliche Zahl n durch eine andere natürliche Zahl t ohne Rest
teilbar, dann heißt t ein Teiler von n. 1 ist Teiler jeder natürlichen Zahl.
Teilbarkeitsregeln: Eine natürliche Zahl ist
– durch 2 teilbar, wenn sie auf 0, 2, 4, 6 oder 8 endet,
– durch 4 teilbar, wenn ihr zweistelliges Ende durch 4 teilbar ist,
– durch 8 teilbar, wenn ihr dreistelliges Ende durch 8 teilbar ist,
– durch 10 teilbar, wenn sie auf 0 endet,
– durch 5 teilbar, wenn sie auf 0 oder 5 endet,
– durch 3 teilbar, wenn ihre Quersumme durch 3 teilbar ist,
– durch 9 teilbar, wenn ihre Quersumme durch 9 teilbar ist,
– durch 6 teilbar, wenn sie durch 2 und durch 3 teilbar ist.
Eine Zahl, die genau zwei Teiler hat, nennt man Primzahl. Primzahlen
sind nur durch 1 und sich selbst ohne Rest teilbar.
Die ersten Primzahlen lauten 2, 3, 5, 7, 11, 13, 17, 19, …
Multipliziert man eine natürliche Zahl der Reihe nach mit
2, 3, 4, 5, 6, 7, …, dann erhält man die Vielfachen dieser Zahl.
Bestimme die Teiler der Zahl 90.
Lösung: Wende zunächst systematisch die Teilbarkeitsregeln an: 1 ist Teiler jeder
Zahl, 90 ist durch 2 teilbar, weil sie auf 0 endet, 90 ist durch 3 teilbar, weil ihre
Quersumme 9 ist, 90 ist nicht durch 4 teilbar, weil ... . Auf diese Weise erhältst
du als Teiler von 90 bereits: 1, 2, 3, 5, 6, 9 und 10. Die restlichen Teiler heißen:
90 : 6 = 15, 90 : 5 = 18, 90 : 3 = 30, 90 : 2 = 45 und 90 selbst.
Antwort: T90 = {1, 2, 3, 5, 6, 9, 10, 15, 18, 30, 45, 90}
Beispiel 1
Bestimme a) die gemeinsamen Teiler, b) den größten gemeinsamen Teiler,
c) die ersten drei gemeinsamen Vielfachen von 24 und 36.
Lösung
a) Teiler von 24: 1, 2, 3, 4, 6, 8, 12, 24
Teiler von 36: 1, 2, 3, 4, 6, 9, 12, 18, 36
Die gemeinsamen Teiler von 24 und 36 sind 1, 2, 3, 4, 6 und 12.
b) Der größte gemeinsame Teiler von 24 und 36 ist 12.
c) Vielfache von 24: 48, 72, 96, 120, 144, 168, 192, 216, 240, …
Vielfache von 36: 72, 108, 144, 180, 216, …
Die ersten drei gemeinsamen Vielfachen von 24 und 36 sind 72, 144, 216.
Beispiel 2
7
3093_Buch.indb 7
13.07.2007 13:06:39
A Grundlagen
3
Rechnen mit natürlichen Zahlen
Addition und Subtraktion
Begriffe, die du kennen solltest:
Summand + Summand
Minuend – Subtrahend
246 + 753
= 999
357 – 246
= 111
Summe
Wert der
Differenz
Wert der
Summe
Differenz
Schriftliche Rechenverfahren
Denke an die Stellenwerttafel des Zehnersystems. Schreibe also Einer
unter Einer, Zehner unter Zehner, Hunderter unter Hunderter usw.
ZT T H Z
3 4 5 3
+ 1 3 1 8
+
5 8
1
2
1
E
3
0
9
4 8 3 0 2
3 4
– 1 0
–
–
8
1
1
5
2
5
4
2
1
0
4
8
1
3
2
1
3
1 5 2 8 7
Sprich: „neun plus null plus drei gleich zwölf.“
Schreibe die Ziffer 2 in die Einerstelle der Antwort
und den Übertrag 1 in die nächste Spalte links.
Sprich: „neun (8+1) plus acht plus drei gleich zwanzig.“ Schreibe die Ziffer 0 in die Zehnerstelle und
den Übertrag 2 in die nächste Spalte links usw.
Sprich: „drei plus eins plus zwei gleich sechs,
plus sieben gleich dreizehn.“
Schreibe die Ziffer 7 in die Einerstelle der Antwort
und den Übertrag 1 in die nächste Spalte links.
Sprich: „neun (8+1) plus vier plus null gleich dreizehn, plus acht gleich einundzwanzig.“
Schreibe die Ziffer 8 in die Zehnerstelle und den
Übertrag 2 in die nächste Spalte links. usw.
Beispiel 1 Einen Näherungswert kannst du durch eine Überschlagsrechnung bestimmen.
a) 517 + 382 + 97 ≈ 500 + 400 + 100 = 1000
b) 4896 – 3109 – 1978 ≈ 5000 – 3000 – 2000 = 0
Beispiel 2
2056 89
–
____________
119 05
Rechne: 5 plus 4 ist 9, schreibe die
4 in die Leerstelle. Weiter: 0 plus 8
ist 8, schreibe ... .
205689
–193784
____________
1
1
11905
8
3093_Buch.indb 8
13.07.2007 13:06:39
3 Rechnen mit natürlichen Zahlen
Multiplikation und Division
Begriffe, die du kennen solltest:
Faktor · Faktor
Dividend : Divisor
120 · 30
= 3600
4800000 : 1200 = 4000
Produkt
Wert des
Quotient
Wert des
Produkts
Quotienten
Schriftliche Rechenverfahren
3 4 9 1 · 8 4 2 Man fasst den zweiten Faktor als Multiplikator auf
und berechnet Teilprodukte.
2 7 9 2 8
Du beginnst mit der höchsten Stelle des
1 3 9 6 4
6 9 8 2 Multiplikators, im Beispiel links multiplizierst du
1 1 2 1
also mit 8 Hundertern.
2 9 3 9 4 2 2 Beim nächsten Teilprodukt rückst du eine Stelle
nach rechts und multiplizierst mit 4 Zehnern,
danach dann noch mit 2 Einern.
Als letztes addierst du die (drei) Teilprodukte.
Überschlag: 3000 · 1000 = 3 000 000
10
6
3
3
24 : 64=16
4
84
84
0
Überschlag:
1020 : 60 = 102 : 6 = 17
Du zerlegst den Dividenden zunächst von vorn
in eine Zifferngruppe, die bei der Division eine
1 oder eine größere Zahl ergibt. Im Beispiel: 102
dividiert durch 64 gleich 1, Rest 38 (Zehner).
Danach addierst du zum Divisionsrest (38 Zehner)
den Wert der nächsten Stelle (4) und erhältst 384
(Einer) und setzt die Division fort: 384 : 64 = 6.
Mögliche Kontrolle:
Die Gegenoperation durchführen.
16 · 64
96
64
1024
Bestimme einen Näherungswert durch eine Überschlagsrechnung.
a) 18 · 22 · 51 ≈ 20 · 20 · 50 = 20 · 1000 = 20 000
b) 39672 : 4006 ≈ 40000 : 4000 = 10
Beispiel 3
Ein Produkt aus drei Faktoren hat den Wert 1000. Ein Faktor heißt 5, ein zweiter
Faktor heißt 8.
Lösung: Nach dem Text gilt: 5 · 8 ·
= 1000 oder 40 ·
= 1000. Den fehlenden
Faktor bestimmst du durch die Gegenoperation 1000 : 40 = 25.
Beispiel 4
9
3093_Buch.indb 9
13.07.2007 13:06:39
A Grundlagen
4
Umfänge und Flächeninhalte
Längeneinheiten
: 10
1 km
: 10
100 m
· 10
: 10
10 m
· 10
: 10
1m
· 10
: 10
1 dm
· 10
: 10
1cm
1mm
· 10
· 10
Den Umfang U eines Vielecks erhältst du als Summe aller Seitenlängen.
U des Rechtecks = 2 · (Länge + Breite): URechteck = 2 · (a + b)
U des Quadrats = 4 · Länge einer Seite UQuadrat = 4 · s
Einheiten des Flächeninhalts
: 100
1 km2
: 100
1ha
(1 Hektar)
· 100
· 100
: 100
: 100
1 m2
1a
(1 Ar)
· 100
: 100
1 dm2
· 100
: 100
1cm2
· 100
1mm2
· 100
Den Flächeninhalt A einer Figur kannst du messen, indem du sie in
Gedanken mit „Einheitsquadraten“ (z.B. vom Flächeninhalt 1 cm2) auslegst.
A des Rechtecks = Länge · Breite:
ARechteck = a· b
A des Quadrats = Länge einer Seite zum Quadrat: AQuadrat = a2
Beispiel 1 Ein Rechteck ist 0,75 m lang und 32 cm breit. Bestimme U und A.
Lösung: Wir rechnen in einer gemeinsamen Längeneinheit, hier mit
75 cm und 32 cm.
URechteck = 2 · (75 cm + 32 cm) = 2 · 107 cm = 214 cm = 2,14 m
ARechteck = 75 cm · 32 cm = 2400 cm2 = 24 dm2 = 0,24 m2
Beispiel 2 Berechne den Umfang und den Flächeninhalt
3,5 m
der abgebildeten Fläche.
Lösung: Zerlege die Gesamtfläche in ein Quadrat
und ein Rechteck, bestimme die fehlenden
3,5 m
Streckenlängen.
U = 3,5 m + 11,5 m + 6 m + 8 m + 2,5 m + 3,5 m = 35 m
A = (3,5 m)2 + 8 m · 6 m = 12,25 m2 + 48 m2 = 60,25 m2
6m
11,5 m
10
3093_Buch.indb 10
13.07.2007 13:06:40
5 Oberflächen und Rauminhalte
5
Oberflächen und Rauminhalte
Körper werden von Flächen begrenzt. Alle Begrenzungsflächen zusammen bilden die Oberfläche des Körpers.
Bei Würfel, Quader, Prisma und
Pyramide sind alle begrenzenden
Flächen eben. Je zwei Flächen stoßen in einer Kante zusammen.
Drei oder mehr Kanten stoßen in
einer Ecke zusammen.
Würfel
Pyramide
Quader
Prisma
Bei Zylinder und Kegel sind die
Mantelflächen gekrümmt, bei der
Kugel die gesamte Oberfläche.
Kegel
Zylinder
Kugel
Einheiten des Rauminhalts
: 1000
1 m3
: 1000
1 dm3
· 1000
Merke dir:
: 1000
1cm3
· 1000
1mm3
· 1000
1 dm3;
1 Liter =
1 Zentiliter = 1 cl = 1 cm3,
1 Milliliter = 1 ml = 1 mm3
Rauminhalt (Volumen) und Oberfläche eines Quaders mit den Kanten
a, b und c bzw. eines Würfels mit der Kante a:
Rauminhalt Quader = Länge · Breite · Höhe
Oberfläche Quader
V = a·b·c
O = 2 · (a · b + a · c + b · c)
Rauminhalt Würfel = Kantenlänge hoch 3
Oberfläche Würfel
V = a3
O = 6 · a2
cm
8 cm
Beispiel
4 cm
4
Bestimme die Oberfläche und den Rauminhalt der
abgebildeten quadratischen Säule.
Lösung: Eine quadratische Säule ist der Sonderfall eines
Quaders, bei dem Länge und Breite gleich groß sind.
O = 2 · a2 + 4 · a · c = 2 · 16 cm2 + 4 · 32 cm2
= 32 cm2 + 128 cm2 = 160 cm2
V = a2 · c = 16 cm2 · 8 cm = 128 cm3
11
3093_Buch.indb 11
13.07.2007 13:06:42
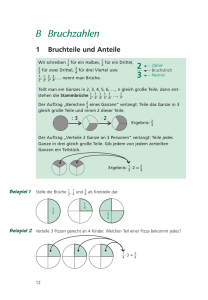
B Bruchzahlen
1
Bruchteile und Anteile
Wir schreiben }12 für ein Halbes, }13 für ein Drittel,
2
3
3
4
2
} für zwei Drittel, } für drei Viertel usw.
3
1 1 2 3
}; }; }; };
2 3 3 4
}}
… nennt man Brüche.
Zähler
Bruchstrich
Nenner
Teilt man ein Ganzes in 2, 3, 4, 5, 6, …, n gleich große Teile, dann ent1
stehen die Stammbrüche }12 , }13, }14 , }15 , }16 , …, }
n.
Der Auftrag „Berechne }23 eines Ganzen“ verlangt: Teile das Ganze in 3
gleich große Teile und nimm 2 dieser Teile.
:3
·2
Ergebnis: }23
Der Auftrag „Verteile 2 Ganze an 3 Personen“ verlangt: Teile jedes
Ganze in drei gleich große Teile. Gib jedem von jedem zerteilten
Ganzen ein Teilstück.
Ergebnis: }13 · 2 = }23
Beispiel 1
Stelle die Brüche }12, }14 und }34 als Kreisteile dar.
1
}
2
1
4
}
3
4
}
Beispiel 2 Verteile 3 Pizzen gerecht an 4 Kinder. Welchen Teil einer Pizza bekommt jedes?
3
4
1
}·3 = }
4
12
3093_Buch.indb 12
13.07.2007 13:06:43
1 Bruchteile und Anteile
Aufgaben
1. Welcher Bruchteil wurde gefärbt?
a)
b)
c)
d)
2. Stelle folgende Bruchteile in den vorbereiteten Figuren dar:
a) }38 ;
5
b) }
;
16
c) }56 .
3. Hier ist eine Strecke von genau 10 cm Länge mit Zentimeter- und Millimetereinteilung gegeben. Markiere
a) }14 der Strecke;
9
25
12
b) }
der Strecke;
c) }}
der Strecke;
d) }}
der Strecke.
10
100
100
7
10
0
1
}
4. Welcher Auftrag ist hier dargestellt? Wie heißt das Ergebnis?
º
º
}} ·
º
º
= }}
5. a) Es sollen 3 Tafeln Schokolade gerecht an 4 Kinder verteilt werden.
b) Es sollen 4 Tafeln Schokolade gerecht an 6 Kinder verteilt werden.
a)
b)
13
3093_Buch.indb 13
13.07.2007 13:06:44
B Bruchteile – Brüche – Bruchzahlen
2
Bruchteile von Größen
Eine Größe ist ein Produkt aus einem Zahlenwert und einer Einheit, wie
15 3 = 15 · 1 3 oder 131 mm = 131 · 1 mm.
a
Bei Bruchteilen von Größen treten Gleichungen der Form }
von G = E
b
auf.
Du musst Aufgaben lösen, in denen zwei von drei Werten gegeben sind.
a
– Berechne den Bruchteil: }
von G = u
b
a
– Berechne das Ganze: }
von u = E
b
u
– Welcher Bruchteil ist E von G? }
u von G = E
Beispiel 1 Berechne }58 von 1200 1. Lösung: (1200 1 : 8) · 5 = 150 1 · 5 = 750 1
Beispiel 2
2
} sind 120 kg. Berechne das Ganze.
3
Lösungsweg I: }13 sind 60 kg (= die Hälfte von 120 kg).
Das Ganze ist dreimal so groß, beträgt also 180 kg.
Lösungsweg II: (u : 3) · 2 = 120 kg.
Rückwärts gerechnet: (120 kg : 2) · 3 = 180 kg.
Beispiel 3 Wie viel sind 20 m2 von 80 m2? Gib den Anteil als Bruch an.
Lösung: 20 m2 sind }14 von 80 m2. Der Bruchteil heißt }14 .
Aufgaben
6. Berechne den Bruchteil.
5
6
a)
} von 60 1 =
b)
} von 120 g =
c)
2
} von 24 m =
9
10
g. Rechnung: 120 g
m.
3
b) }37 von 56 t
8. Was möchtest du lieber haben?
a) }34 von 100 1 oder }35 von 100 1
9. Berechne das Ganze.
a) }14 sind 200 1
: 10
10 1
·5
g
1
·9
g
Rechnung:
7. Berechne den Bruchteil.
1
a) }
von 24 t
15
:6
Rechnung: 60 1
1.
m
3
c) }
von 1 t
10
7
d) }}
von 1 t
100
7
b) }
von 100 1 oder }78 von 100 1
10
b) }34 sind 600 kg
c) }78 sind 5600 km
14
3093_Buch.indb 14
13.07.2007 13:06:45
2 Bruchteile von Größen
10. Gib die farbig markierte Strecke als Teil der ganzen Strecke an
a)
c)
b)
�����������������������������
120 m
d)
�����������������������������
360 m
�����������������������������
400 m
�����������������������������
750 m
11. Wie groß ist die gefärbte Fläche in cm2? Die Rechtecke sind in Originalgröße gezeichnet.
a)
b)
c)
b) 22 1 von 50 1?
e) 18 h von 48 h?
c) 22 1 von 200 1?
f) 20 h von 70 h?
12. Wie viel ist
a) 22 1 von 100 1?
d) 8 h von 24 h?
13. Tessa gibt 8 1 von 30 1, Marc 7 1 von 35 1, Rena 9 1 von 45 1 Taschengeld
für Süßigkeiten aus. Bei wem ist der Anteil am größten, bei wem am
kleinsten?

14. Urlaubszeit. Familie Peters ist seit 10 Tagen an der Ostsee.
a) Fanny Peters meint: „Wir haben noch }13 der Urlaubszeit vor uns.“
b) Vater Peters bemerkt: „Es ist so schön hier. Wir verlängern und haben
erst }59 unserer Zeit herum.“

15. Ein neu gekauftes Auto verliert im ersten Jahr etwa }14 seines Neupreises und
im zweiten Jahr etwa }15 seines Neupreises an Wert.
a) Wie viel ist ein Auto nach zwei Jahren noch wert, wenn es neu
22 400 1 gekostet hat?
b) Ein anderes zwei Jahre altes Auto wird zu 13 585 1 angeboten.

6
4
16. Gesje sagt: „Ich wiege nur }
von meinem Vater plus }
von meiner
10
10
Mutter. Die beiden wiegen zusammen 150 kg.“
15
3093_Buch.indb 15
13.07.2007 13:06:45
B Bruchteile – Brüche – Bruchzahlen
3
Kürzen und Erweitern von Brüchen
Beim Kürzen eines Bruches
werden der Zähler und der
Nenner durch die gleiche Zahl
dividiert.
Beim Erweitern eines Bruches
werden der Zähler und der
Nenner mit der gleichen Zahl
multipliziert.
4
4:2
2
} = }} = }
1
1·2
2
} = }} = }
8
2
2:2
1
} = }} = }
4
8:2
4
4:2
4
2
Man kann auch }48 sofort durch 4
2
2·2
4
} = }} = }
8
8·2
16
1·4
4
erweitern: }}
=}
.
2·4
16
4 2
1
}, } und } bezeichnen gleich
1 2
4
}, } und } bezeichnen gleich
große Bruchteile.
große Bruchteile.
8 4
4 8
2
16
1. Kürzen:
8
8:4
a) }
= }}}
= }23
12
12 : 4
36
36 : 9
b) }
= }}}
= }45
45
45 : 9
60
c) }
= }34
80
2. Erweitern:
3·4
12
a) }38 = }}
=}
8·4
32
8
4·2
b) }45 = }}
=}
5·2
10
5
15
c) }16 = }
=}
30
90
9
1
@
@
36
36
9
=}
= }1
}} = }}
@
@
3. Kurz-Schreibweisen beim Kürzen:
Aufgaben
8
Man kann auch }14 sofort mit 4
4:4
kürzen: }}
= }12 .
8:4
Beispiele
4·2
108
108
27
27
3
3
5
17. Zeige an den vorbereiteten Abbildungen, dass a) }
= }12 und b)
10
ist.
18. Kürze soweit, wie dies möglich ist.
º
º
45 24
6
a) }
= }}
10
9
12
º
º
125 50
} = }}
25
35
45
54 17
b) }
, }, }, }
, }, }}, }.
81 75 36 72 51 75 10
19. a) Erweitere mit 3:
º
º
1
} = }}
2
º
º
} = }}
º
º3 2
2
} = }}
3
40
36
1
4
}=}
3
12
º
º
} = }}
5
8
º
º
7
} = }}
2 4
b) Erweitere jeden Bruch mit 4 (5, 10): }2 , }3, }
, }, }.
11 15 5
º
º
2
} = }}
11
16
3093_Buch.indb 16
13.07.2007 13:06:46
4 Verhältnisse und Maßstäbe
4
Verhältnisse und Maßstäbe
Bei zwei Größen mit gleicher Einheit kann man das Verhältnis bilden.
So ist das Verhältnis von 250 3 zu 1000 3 gleich 250 : 1000 oder gleich
1 : 4 (gelesen „eins zu vier“).
Zur Darstellung bestimmter Objekte benutzt man in der Regel maßstabgetreue Abbildungen oder Zeichnungen.
Ein Maßstab ist das Verhältnis einer Bildlänge zur Originallänge.
In welchem Verhältnis stehen die Gewichte eines Menschen (70 kg) und
eines Elefanten (5,6 t)?
70
1
Lösung: 5,6 t = 5600 kg. Das Gewichtsverhältnis ist 70 : 5600 = }}
=}
.
5600
80
Die Gewichte verhalten sich wie 1 : 80.
Beispiel
20. In welchem Längenverhältnis stehen
Aufgaben
} }
a) AB : BC,
A
} }}
b) AB : CD,
B
} }}
c) BC : CD?
C
D
21. Michael hat den Grundriss vom
Erdgeschoss seines Elternhauses
im Maßstab 1 : 200 aufgezeichnet.
a) Wie lang und breit ist das
Esszimmer (die Küche) in
Wirklichkeit?
b) Passt ein 3,20 m langer
Schrank ins Wohnzimmer?
Und wohin?
Esszimmer
Küche
Wohnzimmer
Flur
Arbeitszimmer
22. Was bedeutet Maßstab 1 : 100 000?
Die Länge einer Bildstrecke verhält sich zur Länge der zugehörigen
wie
. Eine Originalstrecke ist
.
23. Gängige Autokarten haben den Maßstab 1 : 200 000. Jens plant einen
Ausflug. Von A nach B sind es auf der Karte 8,2 cm, von B nach C 9,4 cm
und von C zurück nach A 10,8 cm. Wie lang sind die gesamte Fahrstrecke
und die einzelnen Teilstrecken wirklich?
17
3093_Buch.indb 17
13.07.2007 13:06:47
B Bruchteile – Brüche – Bruchzahlen
5
Bruchzahlen
Wenn man 3 Äpfel an 4 Kinder verteilt, erhält jedes Kind }34 eines Apfels.
Wenn man 3 durch 4 dividiert, erhält man die Bruchzahl }34 .
Die Division einer natürlichen Zahl durch eine natürliche Zahl liefert
eine Bruchzahl. Denke daran: Durch Null darf man nicht dividieren.
Ist der Nenner ein Teiler des Zählers, kann man einen Bruch in eine
natürliche Zahl umformen.
Bruchzahlen, die größer als 1 sind, schreibt man auch als gemischte
Zahlen.
Bruchzahlen kann man der Größe nach ordnen. Dabei ist der
Zahlenstrahl eine Hilfe.
Beispiele
1. 8 : 9 = }89
2. 9 : 8 = }98 = 1 }18
20
3. }
=5
4
4. 0 : 7 = }07 = 0
5. 17 : 5 = (15 + 2) : 5 = 15 : 5 + 2 : 5 = 3 + }25 = 3 }25
9
6. Ordne der Größe nach: }12, 1 }45 , }25 , }
und }54 .
10
2
5
0
}
9
10
1
2
}
}
1
5
4
1 }45
}
2
9
5
2
1
4
} < } < } < } < 1 }.
5
Aufgaben
2
10
4
5
24. Schreibe als gekürzten Bruch, als gemischte Zahl oder als natürliche Zahl.
º º
º º
º=
32 : 4 = }}
º
º=
0 : 100 = }}
º
º º
º º
º = }}
º=
18 : 4 = }}
º º
º=
1000 : 125 = }}
º
a) 10 : 6 = }} = }} =
b) 27 : 18 = }} = }} =
c)
d)
e)
f)
25. Dividiere nach dem Muster von Beispiel 5.
a) 20 : 6
b) 23 : 4
c) 75 : 8
d) 32 : 10
26. Schreibe als Bruch und dann als Quotient aus natürlichen Zahlen.
a) 2 }13
27. a)
3
4
}
b) 3 }12
5
8
}
b) }56
c) 2 }23
d) 5 }14
7
8
13
c) }
10
}
e) 4 }15
6
5
}
d) 2 }13
2 }38
18
3093_Buch.indb 18
13.07.2007 13:06:48
6 Positive rationale Zahlen
6
Positive rationale Zahlen
Natürliche Zahlen und Bruchzahlen werden zur
Menge der positiven rationalen Zahlen mit der
N
Zahl 0 (zu Q +0 ) zusammengefasst. Das Mengenbild
Q +0
zeigt, dass die Menge N eine Teilmenge von Q +0 ist.
Wenn du eine natürliche Zahl a durch eine natürliche Zahl b (ungleich
a
0) dividierst, erhältst du die positive rationale Zahl }
.
b
Dieser Quotient liefert 0, wenn du für a Null wählst, er liefert die Zahl
1, wenn a gleich b ist, und eine natürliche Zahl, wenn du für a ein
Vielfaches von b wählst.
Das Ergebnis einer Division zweier natürlicher Zahlen kannst du auch
als Kommazahl (als Dezimalbruch) schreiben und damit auch eine positive rationale Zahl als Dezimalbruch. Im Alltag rechnet man meistens
mit einer bestimmten Anzahl von Nachkommastellen.
b) 8 : 5 = }85 = 1 }35
8 : 5 = 1,6
5
_
30
30
__
0
a) 2 : 8 = }28 = }14
2 : 8 = 0,25
20
16
__
40
40
__
0
abbrechend
c) 8 : 3 =
8:3 =
_6
20
18
__
20
abbrechend
8
3
2
} = 2}
3
Beispiele
}
2,666... = 2,6
}
2,6 wird gelesen:
„zwei Periode
sechs“
periodisch
Aufgaben
28. Ordne die Zahlen }14; 1; 0,4; }74; 1 }12 der Größe nach.
<
<
<
<
29. Gib den Quotienten als Bruch und als Dezimalbruch an.
a) 1 : 4
e) 5 : 40
b) 2 : 5
f) 6 : 30
c) 3 : 10
g) 7 : 5
d) 4 : 25
h) 8 : 100
19
3093_Buch.indb 19
13.07.2007 13:06:48
C Rechnen mit Brüchen
1
Addieren und Subtrahieren
Brüche mit gleichem Nenner werden addiert (subtrahiert), indem man
die Zähler addiert (subtrahiert) und den gemeinsamen Nenner beibehält.
Sind die Nenner der Brüche verschieden, so bringt man die Brüche
durch Erweitern oder Kürzen auf den gleichen Nenner, bevor man sie
addiert oder subtrahiert.
In diesen Fällen ist es oft ratsam, den Hauptnenner der beteiligten
Brüche zu bestimmen und die Brüche entsprechend umzuformen („auf
den Hauptnenner zu bringen“.)
Beispiel 1 a)
15
7
22
}+}=}=2
5
6
11
b) }
–}
=}
= }12
12 12
12
Beispiel 2 a)
3
5
1
1
2
}+}=}+}=}
3
18
3
15
b) }95 – }
=}
–}
=}
= }32 1 = 1 }12 2
10
10 10
10
11
3
11
2
11
6
Beispiel 3 Rechne aus:
6
6
13 6
c) 2 }35 – 1 }15 = }
– }5 = }75 = 1 }25
5
5
5
7
}+}–}
18
24
36
Lösung: Bestimme den Hauptnenner.
Die Vielfachen von 18 sind: 36, 54, 72, 90, 108, ...
Die Vielfachen von 24 sind: 48, 72, 96, 120, 144, ...
Die Vielfachen von 36 sind: 72, 108, 144,...
Der Hauptnenner ist das kleinste gemeinsame Vielfache (das kgV) von 18, 24
und 36, hier also 72.
5
5
20
31
7
21 10
Rechnung: }
+}
–}
=}
+}
–}=}
18
24 36
72
72 72
72
Aufgaben
1. Rechne im Kopf. Kürze das Ergebnis, falls möglich.
3
9
a) }
+}
14
14
25
11
b) }
+}
12
12
41 29
c) }
–}
15 15
d) 5 – }23
5
7
e) }
–}
20 20
f) 1 – }23
g) 1 }12 + 3 }12
h) 3 }13 – 2 }23
20
3093_Buch.indb 20
13.07.2007 13:06:50
1 Addieren und Subtrahieren
º
º
11
7
º=
c) }
+ }9 = }}
9
º
8
1
º
e) }} – }
=}
10
10
º
2. a)
3
8
5
8
º
º
7
2
b) }
–}
= }} =
10 10
} + } = }} =
º
º
º
º
d) }18 + }} = }48 = }}
º
º
f) }} + }25 = 1 }15
º
º
5
6
4
7
g) }
+}
+}
+}
= }}} =
11
11
11
11
º
º
19 3 4 5
h) }
– }7 – }7 – }7 = }} =
7
3. Berechne und kürze, falls möglich
a) }14 + }18
b) }23 – }16
c) }56 – }13
13 5
d) }
–}
12 6
e) }23 + }16
9
f) }45 + }
10
g) }87 + }12
5
h) }
+ }53
12
4. a)
º
º
3
5
º
º
3
4
3
4
4
} + }} = 1 } b) }} – } = }
5
5. Wahr (w) oder falsch (f)?
º
º
º
º
7
7
c) }23 – }} = }
d) }} + }34 = }
12
12
a) }34 + }14 < }54 + }14
10
b) }34 von 6 > }23 + }
3
c) }38 – }18 > }73 – }63
28 18
4
7
d) }
+}
<}
–}
11
11
10 10
21
21
e) }25 von 5 < }
+}
20
20
9
27
f) }
+}
= }51 – }21
12
12
6. a) }34 + }18 – }12
5
1
7
 d) }
+}
+}
12
18
24
b) }56 – }13 + }16
7
c) }
+ }34 – }56
12
6
7
7
 e) }
–}
+}
15 18
30
11
4
7
 f) }
+}
–}
20
25 10
1
1
1
7. a) Berechne den Wert der Summe }12 + }14 + }18 + }
+}
+}
.
16
32
64
b) Gib eine natürliche Zahl als Näherungswert für die Summe an.
8. Auf dem Tisch stehen eine }13-Liter-, eine }12-Liter- und eine Ein-Liter-Flasche.
Alle sind mit Wasser randvoll gefüllt. Leon gießt alles in eine 2-LiterFlasche. Wie viel Wasser fehlt noch, damit die große Flasche ganz voll ist?

9. Sophie sagt: „Ich habe }34 plus }38 plus }18 von 200 1 auf meinem Sparbuch.
Für einen neuen Laptop brauche ich aber 4-mal so viel Geld.“ Wie viele
Euro fehlen ihr?
21
3093_Buch.indb 21
13.07.2007 13:06:50
C Rechnen mit Brüchen
2
Multiplizieren
Ein Bruch wird mit einer natürlichen Zahl multipliziert, indem man den
Zähler mit der natürlichen Zahl multipliziert und den Nenner beibehält.
a
b
a·n
b
} · n = }} für alle a, b, n * N, b Ð 0
Ein Bruch wird mit einem Bruch multipliziert, indem man Zähler mit
Zähler und Nenner mit Nenner multipliziert.
a
b n
a·m
b·n
m
} · } = }} für alle a, b, m, n * N, b Ð 0, n Ð 0
Gemischte Zahlen werden vorher in Brüche umgeformt.
55
11
c) 2 }34 · 5 = }
·5 = }
= 13 }34
4
4
Beispiele
3·1
a) 3 · }14 = }}
= }34
4
Aufgaben
10. a)
4 · }23
b)
7 · }19
c)
}·2
18
3
d)
}·7
1
14
e)
} · 11
f)
}·}
3 1
4 2
g)
}·}
2 5
3 6
h)
}·}
4 15
5 16
i)
}·}
9 8
8 9
j)
}·}
11. a)
2
3
3·9
27
b) }34 · }98 = }}
=}
4 ·8
32
= }43

13. a)
= }58
}·
2 2
4
}·} < }
b)
5 1
1
}·} > }
2 · }34 · 4 · }18
b)
}·}·5·}
12. Wahr (w) oder falsch (f)?
a)
5
4
b)
}·
3 3
6
1 5
4 3
9 10
2
1
20
6
11
4 6
4 5
· }27 = }72
c)
c)
3 2
1
}·} < }
c)
1 1
12 · 4 · }
·}
12 4
4 3
2
14. Familie Mair plant eine große Wanderung.
a)
b)
Vater schlägt vor, morgens aufzubrechen, zunächst 2 Stunden zu
gehen, dann eine Pause von 30 Minuten einzulegen und danach noch
1 }14 Stunden zu wandern. Wie viel km würden sie bis zum Mittag
schaffen, wenn sie stündlich 4 }12 km wandern?
Vaters Plan wird eingehalten. Sie schaffen aber nur 4 }14 km/h.
15. Berechne U und A eines Rechtecks, das 1 }14 m lang und }34 m breit ist.
22
3093_Buch.indb 22
13.07.2007 13:06:51
3 Dividieren
3
Dividieren
Ein Bruch wird durch eine natürliche Zahl dividiert, indem man den
Zähler durch die natürliche Zahl dividiert und den Nenner beibehält.
Ist der Divisor kein Teiler des Zählers, dann rechnet man nach dem
Standardverfahren:
a
b
a
b·n
} : n = }}
für a, b, n * N, b Ð 0, n Ð 0.
Man dividiert durch einen Bruch, indem man mit seinem Kehrwert multipliziert („Kehrwertregel“).
a
b n
a
b m
a·n
b·m
m
n
}:}
= }·}
= }}
14
a) }
: 7 = }23
3
für a, b, m, n * N, b, m, n Ð 0
2
·3
8
c) }87 : }43 = }87 · }34 = }}
= }67
4
7·@
12
12 1
12
b) }
:5 = }
·} = }
5
5 5
25
@
Beispiele
1
16. a)
}:3
3
4
b)
}:2
3
4
c)
}:5
3
4
d)
}:6
e)
}:4
2
3
f)
}:5
2
3
g)
}:7
3
7
h)
} : 10
Aufgaben
3
4
1
10
17. Bilde den Kehrwert von a) }35, b) }34, c) }54, d) }78, e) 6, f) 10, g) 1.
18. a)
}:}
3 7
4 8
b)
}:}
2 6
3 5
c)
}:}
7 10
5 7
d)
}:}
19. a)
1 }34 : 7
b)
2 }23 : 16
c)
8
1 }35 : }
10
d)
5 5
1}
:}
12 24
20. a)
Der Umfang eines Rechtecks beträgt 15 }12 m. Es ist 5 }12 m lang.
b)
2 7
5 5
Für ein anderes Rechteck gilt: A = 38 m2. Es ist 8 m breit.
21. Aus einem 50-Liter-Fass mit Speiseöl sollen
a)
b)
c)
Wie
Flaschen mit }12 Liter Inhalt,
Flaschen mit }34 Liter Inhalt,
Flaschen mit 0,7 Liter Inhalt abgefüllt werden.
viele Flaschen werden jeweils gefüllt?
23
3093_Buch.indb 23
13.07.2007 13:06:52