B Bruchzahlen

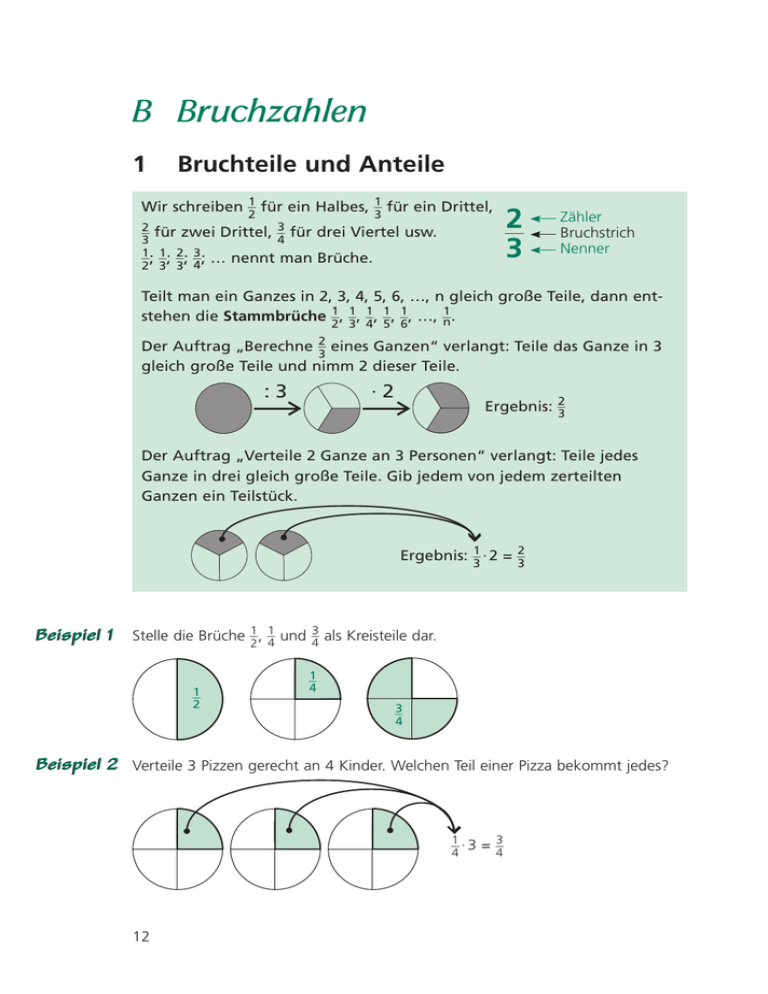
B Bruchzahlen
1
Bruchteile und Anteile
Wir schreiben }12 für ein Halbes, }13 für ein Drittel,
2
3
3
4
2
} für zwei Drittel, } für drei Viertel usw.
3
1 1 2 3
}; }; }; };
2 3 3 4
}}
… nennt man Brüche.
Zähler
Bruchstrich
Nenner
Teilt man ein Ganzes in 2, 3, 4, 5, 6, …, n gleich große Teile, dann ent1
stehen die Stammbrüche }12 , }13 , }14 , }15, }16 , …, }
n.
Der Auftrag „Berechne }23 eines Ganzen“ verlangt: Teile das Ganze in 3
gleich große Teile und nimm 2 dieser Teile.
:3
·2
Ergebnis: }23
Der Auftrag „Verteile 2 Ganze an 3 Personen“ verlangt: Teile jedes
Ganze in drei gleich große Teile. Gib jedem von jedem zerteilten
Ganzen ein Teilstück.
Ergebnis: }13 · 2 = }23
Beispiel 1
Stelle die Brüche }12, }14 und }34 als Kreisteile dar.
1
}
2
1
4
}
3
4
}
Beispiel 2 Verteile 3 Pizzen gerecht an 4 Kinder. Welchen Teil einer Pizza bekommt jedes?
3
4
1
}·3 = }
4
12
1 Bruchteile und Anteile
Aufgaben
1. Welcher Bruchteil wurde gefärbt?
a)
b)
c)
d)
2. Stelle folgende Bruchteile in den vorbereiteten Figuren dar:
a) }38 ;
5
b) }
;
16
c) }56.
3. Hier ist eine Strecke von genau 10 cm Länge mit Zentimeter- und Millimetereinteilung gegeben. Markiere
a) }14 der Strecke;
9
25
12
b) }
der Strecke;
c) }}
der Strecke;
d) }}
der Strecke.
10
100
100
7
10
0
1
}
4. Welcher Auftrag ist hier dargestellt? Wie heißt das Ergebnis?
º
º
}} ·
º
º
= }}
5. a) Es sollen 3 Tafeln Schokolade gerecht an 4 Kinder verteilt werden.
b) Es sollen 4 Tafeln Schokolade gerecht an 6 Kinder verteilt werden.
a)
b)
13
B Bruchteile – Brüche – Bruchzahlen
2
Bruchteile von Größen
Eine Größe ist ein Produkt aus einem Zahlenwert und einer Einheit, wie
15 3 = 15 · 1 3 oder 131 mm = 131 · 1 mm.
a
Bei Bruchteilen von Größen treten Gleichungen der Form }
von G = E
b
auf.
Du musst Aufgaben lösen, in denen zwei von drei Werten gegeben sind.
a
– Berechne den Bruchteil: }
von G = u
b
a
– Berechne das Ganze: }
von u = E
b
u von G = E
– Welcher Bruchteil ist E von G? }
u
Beispiel 1 Berechne }58 von 1200 1. Lösung: (1200 1 : 8) · 5 = 150 1 · 5 = 750 1
Beispiel 2
2
} sind 120 kg. Berechne das Ganze.
3
Lösungsweg I: }13 sind 60 kg (= die Hälfte von 120 kg).
Das Ganze ist dreimal so groß, beträgt also 180 kg.
Lösungsweg II: (u : 3) · 2 = 120 kg.
Rückwärts gerechnet: (120 kg : 2) · 3 = 180 kg.
Beispiel 3 Wie viel sind 20 m2 von 80 m2? Gib den Anteil als Bruch an.
Lösung: 20 m2 sind }14 von 80 m2. Der Bruchteil heißt }14 .
Aufgaben
6. Berechne den Bruchteil.
5
6
a)
} von 60 1 =
b)
} von 120 g =
c)
2
} von 24 m =
9
10
g. Rechnung: 120 g
m.
3
b) }37 von 56 t
8. Was möchtest du lieber haben?
a) }34 von 100 1 oder }35 von 100 1
9. Berechne das Ganze.
a) }14 sind 200 1
14
: 10
10 1
·5
g
1
·9
Rechnung:
7. Berechne den Bruchteil.
1
a) }
von 24 t
15
:6
Rechnung: 60 1
1.
m
3
c) }
von 1 t
10
7
d) }}
von 1 t
100
7
b) }
von 100 1 oder }78 von 100 1
10
b) }34 sind 600 kg
g
c) }78 sind 5600 km
2 Bruchteile von Größen
10. Gib die farbig markierte Strecke als Teil der ganzen Strecke an
a)
c)
b)
�����������������������������
120 m
d)
�����������������������������
360 m
�����������������������������
400 m
�����������������������������
750 m
11. Wie groß ist die gefärbte Fläche in cm2? Die Rechtecke sind in Originalgröße gezeichnet.
a)
b)
c)
b) 22 1 von 50 1?
e) 18 h von 48 h?
c) 22 1 von 200 1?
f) 20 h von 70 h?
12. Wie viel ist
a) 22 1 von 100 1?
d) 8 h von 24 h?
13. Tessa gibt 8 1 von 30 1, Marc 7 1 von 35 1, Rena 9 1 von 45 1 Taschengeld
für Süßigkeiten aus. Bei wem ist der Anteil am größten, bei wem am
kleinsten?

14. Urlaubszeit. Familie Peters ist seit 10 Tagen an der Ostsee.
a) Fanny Peters meint: „Wir haben noch }13 der Urlaubszeit vor uns.“
b) Vater Peters bemerkt: „Es ist so schön hier. Wir verlängern und haben
erst }59 unserer Zeit herum.“

15. Ein neu gekauftes Auto verliert im ersten Jahr etwa }14 seines Neupreises und
im zweiten Jahr etwa }15 seines Neupreises an Wert.
a) Wie viel ist ein Auto nach zwei Jahren noch wert, wenn es neu
22 400 1 gekostet hat?
b) Ein anderes zwei Jahre altes Auto wird zu 13 585 1 angeboten.

6
4
16. Gesje sagt: „Ich wiege nur }
von meinem Vater plus }
von meiner
10
10
Mutter. Die beiden wiegen zusammen 150 kg.“
15
B Bruchteile – Brüche – Bruchzahlen
3
Kürzen und Erweitern von Brüchen
Beim Kürzen eines Bruches
werden der Zähler und der
Nenner durch die gleiche Zahl
dividiert.
Beim Erweitern eines Bruches
werden der Zähler und der
Nenner mit der gleichen Zahl
multipliziert.
4
4:2
2
} = }} = }
1
1·2
2
} = }} = }
8
8:2
2
2:2
1
} = }} = }
4
4
Man kann auch
4:2
4
}
8
4
2
sofort durch 4
4:4
kürzen: }}
= }12 .
8:4
4 2
1
}, } und } bezeichnen
8 4
2
erweitern:
1 2
}, }
4 8
gleich
8
8·2
und
4
}
16
1·4
}}
2·4
1
}
4
=
16
sofort mit 4
4
}.
16
bezeichnen gleich
große Bruchteile.
1. Kürzen:
8
8:4
a) }
= }}}
= }23
12
12 : 4
36
36 : 9
b) }
= }}}
= }45
45
45 : 9
60
c) }
= }34
80
2. Erweitern:
3·4
12
a) }38 = }}
=}
8·4
32
8
4·2
b) }45 = }}
=}
5·2
10
5
15
c) }16 = }
=}
30
90
9
1
@
@
36
36
9
=}
= }1
}} = }}
@
@
3. Kurz-Schreibweisen beim Kürzen:
Aufgaben
2
2·2
4
} = }} = }
8
Man kann auch
große Bruchteile.
Beispiele
4·2
108
108
27
27
3
3
5
17. Zeige an den vorbereiteten Abbildungen, dass a) }
= }12 und b)
10
ist.
18. Kürze soweit, wie dies möglich ist.
º
º
45 24
6
a) }
= }}
10
9
12
º
º
125 50
} = }}
25
35
45
54 17
b) }
, }, }, }
, }, }}, }.
81 75 36 72 51 75 10
19. a) Erweitere mit 3:
º
º
1
} = }}
2
º
º
} = }}
º
º3 2
2
} = }}
3
40
36
3
º
º
} = }}
5
8
º
º
7
} = }}
2 4
b) Erweitere jeden Bruch mit 4 (5, 10): }2 , }3 , }
, }, }.
11 15 5
16
1
4
}=}
º
º
2
} = }}
11
12
4 Verhältnisse und Maßstäbe
4
Verhältnisse und Maßstäbe
Bei zwei Größen mit gleicher Einheit kann man das Verhältnis bilden.
So ist das Verhältnis von 250 3 zu 1000 3 gleich 250 : 1000 oder gleich
1 : 4 (gelesen „eins zu vier“).
Zur Darstellung bestimmter Objekte benutzt man in der Regel maßstabgetreue Abbildungen oder Zeichnungen.
Ein Maßstab ist das Verhältnis einer Bildlänge zur Originallänge.
In welchem Verhältnis stehen die Gewichte eines Menschen (70 kg) und
eines Elefanten (5,6 t)?
70
1
Lösung: 5,6 t = 5600 kg. Das Gewichtsverhältnis ist 70 : 5600 = }}
=}
.
5600
80
Die Gewichte verhalten sich wie 1 : 80.
Beispiel
20. In welchem Längenverhältnis stehen
Aufgaben
} }
a) AB : BC,
A
} }}
b) AB : CD,
B
} }}
c) BC : CD?
C
D
21. Michael hat den Grundriss vom
Erdgeschoss seines Elternhauses
im Maßstab 1 : 200 aufgezeichnet.
a) Wie lang und breit ist das
Esszimmer (die Küche) in
Wirklichkeit?
b) Passt ein 3,20 m langer
Schrank ins Wohnzimmer?
Und wohin?
Esszimmer
Küche
Wohnzimmer
Flur
Arbeitszimmer
22. Was bedeutet Maßstab 1 : 100 000?
Die Länge einer Bildstrecke verhält sich zur Länge der zugehörigen
wie
. Eine Originalstrecke ist
.
23. Gängige Autokarten haben den Maßstab 1 : 200 000. Jens plant einen
Ausflug. Von A nach B sind es auf der Karte 8,2 cm, von B nach C 9,4 cm
und von C zurück nach A 10,8 cm. Wie lang sind die gesamte Fahrstrecke
und die einzelnen Teilstrecken wirklich?
17
B Bruchteile – Brüche – Bruchzahlen
5
Bruchzahlen
Wenn man 3 Äpfel an 4 Kinder verteilt, erhält jedes Kind }34 eines Apfels.
Wenn man 3 durch 4 dividiert, erhält man die Bruchzahl }34 .
Die Division einer natürlichen Zahl durch eine natürliche Zahl liefert
eine Bruchzahl. Denke daran: Durch Null darf man nicht dividieren.
Ist der Nenner ein Teiler des Zählers, kann man einen Bruch in eine
natürliche Zahl umformen.
Bruchzahlen, die größer als 1 sind, schreibt man auch als gemischte
Zahlen.
Bruchzahlen kann man der Größe nach ordnen. Dabei ist der
Zahlenstrahl eine Hilfe.
Beispiele
1. 8 : 9 = }89
2. 9 : 8 = }98 = 1 }18
20
3. }
=5
4
4. 0 : 7 = }07 = 0
5. 17 : 5 = (15 + 2) : 5 = 15 : 5 + 2 : 5 = 3 + }25 = 3 }25
9
6. Ordne der Größe nach: }12 , 1 }45, }25, }
und }54.
10
2
5
0
}
9
10
1
2
}
}
1
5
4
1 }45
}
2
9
5
2
1
4
} < } < } < } < 1 }.
5
Aufgaben
2
10
4
5
24. Schreibe als gekürzten Bruch, als gemischte Zahl oder als natürliche Zahl.
º º
º º
º=
32 : 4 = }}
º
º=
0 : 100 = }}
º
º º
º º
º = }}
º=
18 : 4 = }}
º º
º=
1000 : 125 = }}
º
a) 10 : 6 = }} = }} =
b) 27 : 18 = }} = }} =
c)
d)
e)
f)
25. Dividiere nach dem Muster von Beispiel 5.
a) 20 : 6
b) 23 : 4
c) 75 : 8
d) 32 : 10
26. Schreibe als Bruch und dann als Quotient aus natürlichen Zahlen.
a) 2 }13
27. a)
18
3
4
}
b) 3 }12
5
8
}
b) }56
c) 2 }23
d) 5 }14
7
8
13
c) }
10
}
e) 4 }15
6
5
}
d) 2 }13
2 }38
6 Positive rationale Zahlen
6
Positive rationale Zahlen
Natürliche Zahlen und Bruchzahlen werden zur
Menge der positiven rationalen Zahlen mit der
N
Zahl 0 (zu Q +0 ) zusammengefasst. Das Mengenbild
Q +0
zeigt, dass die Menge N eine Teilmenge von Q +0 ist.
Wenn du eine natürliche Zahl a durch eine natürliche Zahl b (ungleich
a
0) dividierst, erhältst du die positive rationale Zahl }
.
b
Dieser Quotient liefert 0, wenn du für a Null wählst, er liefert die Zahl
1, wenn a gleich b ist, und eine natürliche Zahl, wenn du für a ein
Vielfaches von b wählst.
Das Ergebnis einer Division zweier natürlicher Zahlen kannst du auch
als Kommazahl (als Dezimalbruch) schreiben und damit auch eine positive rationale Zahl als Dezimalbruch. Im Alltag rechnet man meistens
mit einer bestimmten Anzahl von Nachkommastellen.
b) 8 : 5 = }85 = 1 }35
8 : 5 = 1,6
5
_
30
30
__
0
a) 2 : 8 = }28 = }14
2 : 8 = 0,25
20
16
__
40
40
__
0
abbrechend
c) 8 : 3 =
8:3 =
_6
20
18
__
20
abbrechend
8
3
2
} = 2}
3
Beispiele
}
2,666... = 2,6
}
2,6 wird gelesen:
„zwei Periode
sechs“
periodisch
Aufgaben
28. Ordne die Zahlen }14; 1; 0,4; }74; 1 }12 der Größe nach.
<
<
<
<
29. Gib den Quotienten als Bruch und als Dezimalbruch an.
a) 1 : 4
e) 5 : 40
b) 2 : 5
f) 6 : 30
c) 3 : 10
g) 7 : 5
d) 4 : 25
h) 8 : 100
19