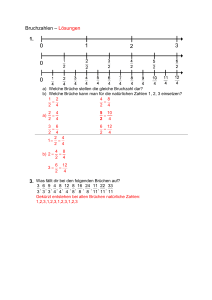
Arbeitsblatt 3 - Bruchzahlen der Größe nach ordnen

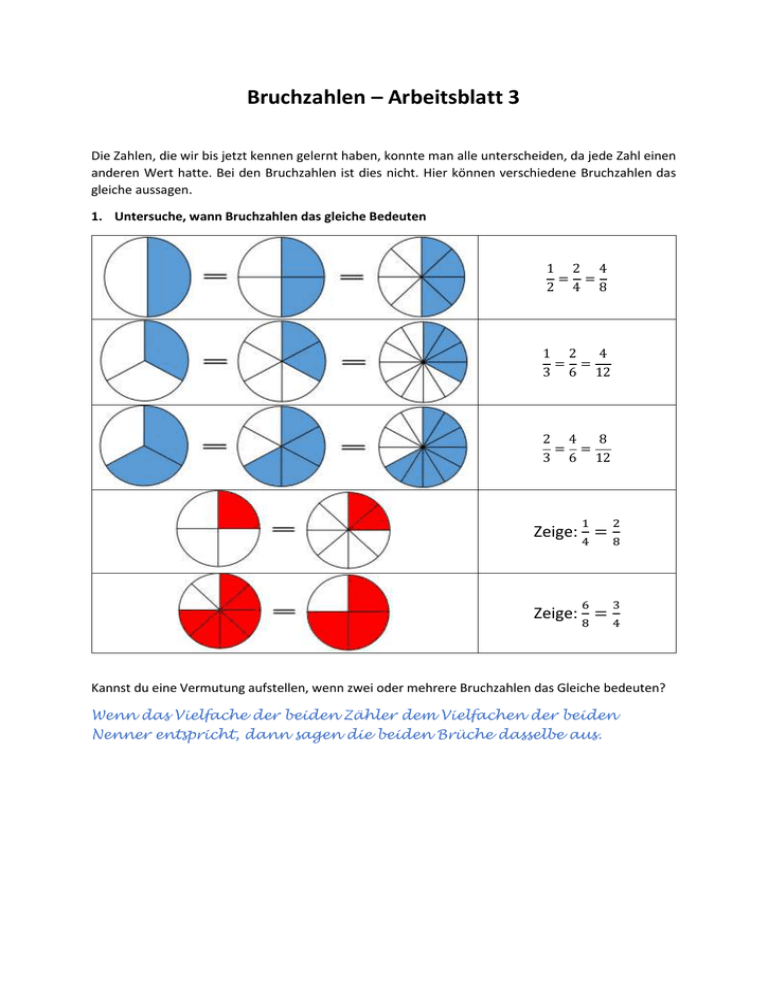
Bruchzahlen – Arbeitsblatt 3
Die Zahlen, die wir bis jetzt kennen gelernt haben, konnte man alle unterscheiden, da jede Zahl einen
anderen Wert hatte. Bei den Bruchzahlen ist dies nicht. Hier können verschiedene Bruchzahlen das
gleiche aussagen.
1. Untersuche, wann Bruchzahlen das gleiche Bedeuten
1 2 4
= =
2 4 8
1 2
4
= =
3 6 12
2 4
8
= =
3 6 12
1
2
4
8
6
3
8
4
Zeige: =
Zeige: =
Kannst du eine Vermutung aufstellen, wenn zwei oder mehrere Bruchzahlen das Gleiche bedeuten?
Wenn das Vielfache der beiden Zähler dem Vielfachen der beiden
Nenner entspricht, dann sagen die beiden Brüche dasselbe aus.
2. Ordnung von Bruchzahlen I
Genauso wie die Zahlen, die wir bis jetzt kennen gelernt haben lassen sich auch Bruchzahlen der Größe
1
1
nach ordnen. Aber Achtung, es gilt zwar 2 < 4, aber 2 > 4. Begründe dies sowohl graphisch als auch
mit Worten.
Erklärung: Beim Vierteln wird ein Objekt in mehrere kleinere Teile zerlegt,
darum muss ein Halb größer sein als ein Viertel
3. Ordnung von Bruchzahlen II
Ordne die gegebenen Bruchzahlen der Größe nach. Du kannst zur Hilfe die Bruchzahlen am Folgeblatt
grafisch darstellen.
1 1 1
, ,
2 3 4
1 1 1
, ,
2 6 3
2 1 2
, ,
5 7 7
3 1 4
, ,
8 4 5
1 1 1
, ,
7 8 2
1 3 2
, ,
5 6 8
3 1 2
, ,
4 2 7
1 3 4
, ,
2 8 7
1 1 1
< <
4 3 2
1 1 1
< <
6 3 2
1 2 2
< <
7 7 5
1 3 4
< <
4 8 5
1 1 1
< <
8 7 2
1 2 3
< <
5 8 6
2 1 3
< <
7 2 4
3 1 4
< <
8 2 7
1 1
3 , ,2
4 2
1 3
, 8,
8 8
1 3 4
2 , ,
7 2 7
1 4 7
2 , 2 , 1,
7 5 8
1 4 2
4 ,3 ,1
4 6 7
2 1 4
, ,
2 3 5
1 1 1
, ,
2 6 8
4 1
3, , 2
8 3
1
1
<2<3
2
4
1 3
< <8
8 8
4 3
1
< <2
7 2
7
7
1
4
1 <2 <2
8
7
5
2
4
1
1 <3 <4
7
6
4
1 4 2
< <
3 5 2
1 1 1
< <
8 6 2
4
1
<2 <3
8
3