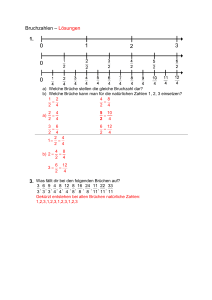
Systembrüche als Darstellung von Bruchzahlen
Werbung
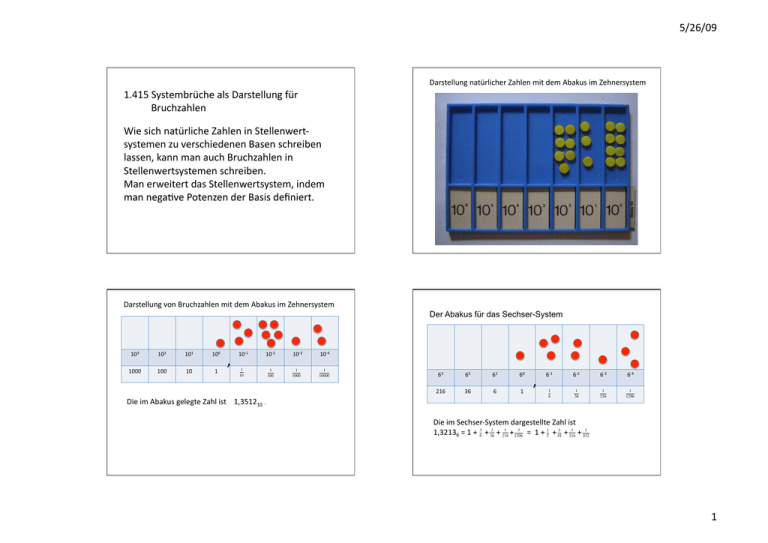
5/26/09 Darstellung natürlicher Zahlen mit dem Abakus im Zehnersystem 1.415 Systembrüche als Darstellung für Bruchzahlen Wie sich natürliche Zahlen in Stellenwert‐ systemen zu verschiedenen Basen schreiben lassen, kann man auch Bruchzahlen in Stellenwertsystemen schreiben. Man erweitert das Stellenwertsystem, indem man negaIve Potenzen der Basis definiert. Darstellung von Bruchzahlen mit dem Abakus im Zehnersystem Der Abakus für das Sechser-System 103 102 101 1000 100 10 100 , 1 € 10‐1 10‐2 1 10 1 100 € € 10‐3 10‐4 1 1000 1 10000 € 63 62 61 60 216 36 6 1 , Die im Abakus gelegte Zahl ist 1,351210 . 6‐1 6‐2 6‐3 6‐4 1 6 1 36 1 216 1 1296 € € € € Die im Sechser‐System dargestellte Zahl ist 2 1 1 1 1 3 3 1 1,32136 = 1 + + + + = 1 + + + + 36 216 1296 216 18 432 6 2 € € € € € € € € 1 5/26/09 ∈ Für p,q IN , ggT(p,q) = 1 und p < q gibt es eine Darstellungsform für die Bruchzahl Brüche im Sechsersystem € p q ∞ = ∑a b i=1 i i = a b 1 + a b 2 2 + a b 3 3 + . . . die Systembruchdarstellung. € Beispiele für Systembrüche: 35 Systembruchdarstellung von zur Basis 6 72 € 2 5/26/09 Abbrechende und nicht‐abbrechende Systembrüche WichIge Einsicht: Die Systembruchdarstellung (in der Schule meistens: die Dezimalbruchdarstellung) erlaubt es, die bekannten schri\lichen Rechenverfahren für natürliche Zahlen auf Bruchzahlen (in Systembruchdarstellung) zu übertragen. Im Zusammenhang damit werden Übungen mit dem Taschenrechner durchgeführt. Die prakIsche Frage ist dabei: wie viel Stellen muss ein Taschenrechner anzeigen (bzw. mit wie vielen muss er intern rechnen), damit er für besImmt Belange ausreicht? 3