( ) ( )x

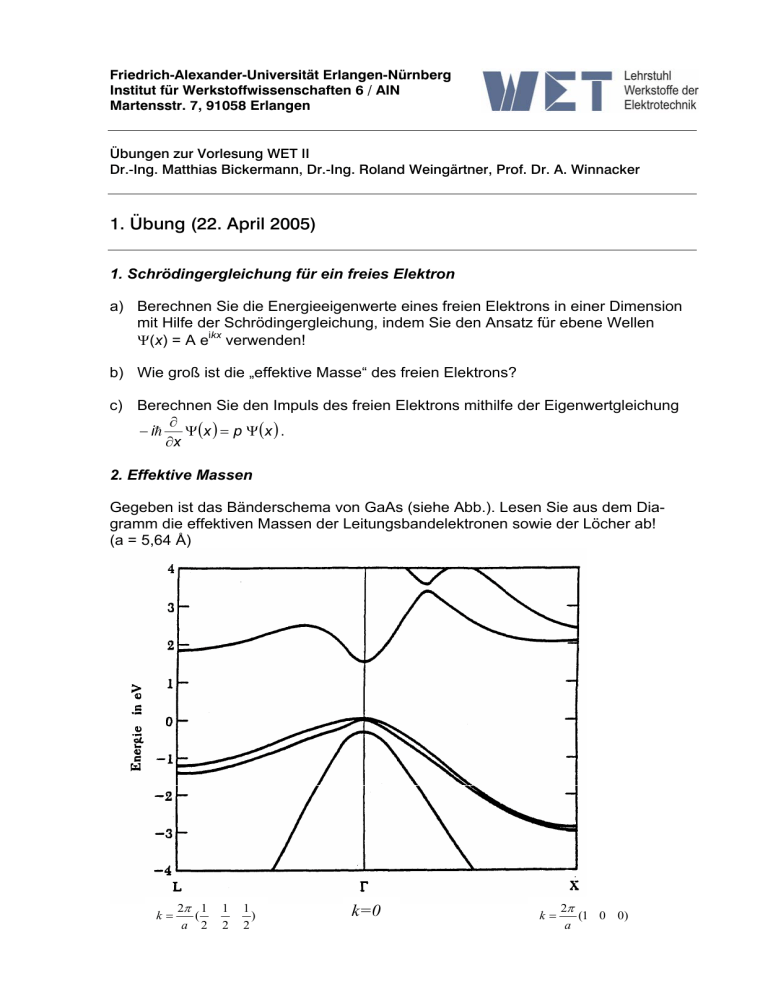
Friedrich-Alexander-Universität Erlangen-Nürnberg
Institut für Werkstoffwissenschaften 6 / AlN
Martensstr. 7, 91058 Erlangen
Übungen zur Vorlesung WET II
Dr.-Ing. Matthias Bickermann, Dr.-Ing. Roland Weingärtner, Prof. Dr. A. Winnacker
1. Übung (22. April 2005)
1. Schrödingergleichung für ein freies Elektron
a) Berechnen Sie die Energieeigenwerte eines freien Elektrons in einer Dimension
mit Hilfe der Schrödingergleichung, indem Sie den Ansatz für ebene Wellen
Ψ(x) = A eikx verwenden!
b) Wie groß ist die „effektive Masse“ des freien Elektrons?
c) Berechnen Sie den Impuls des freien Elektrons mithilfe der Eigenwertgleichung
∂
− ih Ψ (x ) = p Ψ (x ) .
∂x
2. Effektive Massen
Gegeben ist das Bänderschema von GaAs (siehe Abb.). Lesen Sie aus dem Diagramm die effektiven Massen der Leitungsbandelektronen sowie der Löcher ab!
(a = 5,64 Å)
k=
2π 1
(
a 2
1
2
1
)
2
k=0
k=
2π
(1 0 0)
a
3. Teilchen im Kastenpotential
a) Skizzieren Sie das „Kasten-Potential“:
⎧⎪ 0 für x < a
2
V (x ) = ⎨
a
∞
für
x
≥
⎪⎩
2
b) Berechnen Sie die Energieeigenwerte von einem Teilchen im Kastenpotential V.
Verwenden Sie hierfür den Lösungsansatz Ψ (x ) = A sin kx + B cos kx !
c) Welche Einschränkung für k ergibt sich aus den Zwangsbedingungen
Ψ − a = 0 und Ψ + a = 0 ?
2
2
Wie berechnen sich mit diesem k die Energieeigenwerte?
( )
( )
d) Berechnen Sie die Energie für den Übergang vom Grundzustand in den ersten
angeregten Zustand in Abhängigkeit von a!