Nicht jede Formel, die in dieser Sammlung aufgenommen ist, muss

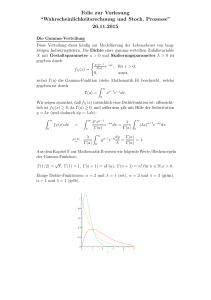
-1-
Formelsammlung zur Klausur Induktive Statistik
Prof. Dr. Nikolaus
Wolik
Hinweis: Nicht jede Formel, die in dieser Sammlung aufgenommen ist, muss auch zur
Lösung der Klausur herangezogen werden.
1. Kombinatorische Grundlagen
Permutationen:
ohne Wiederholung:
P(n) = n!
Mit Wiederholung:
P(n1,n2 ,...,nk ) =
n!
n1 !n2 !⋅ ... ⋅ nk !
Kombinationen und Variationen:
n
n!
 =
 k  k!(n − k)!
Ohne
Ziehung
Zurücklegen
Mit Berücksichtigung
der Reihenfolge
Mit Zurücklegen
n
Vk (n) = k!  
k 
Vk` (n) = nk
 n
Ck (n) =  
k
 n + k − 1
Ck` (n) = 

 k 
Ohne Berücksichtigung
der Reihenfolge
2. Wahrscheinlichkeiten
Laplace`scher Wahrscheinlichkeitsbegriff:
P=
Anzahl günstiger Fälle
Anzahl gleichmöglicher Fälle
Für Ereignisse A und B gilt:
P(A) ≥ 0
P(Ω ) = 1
P(∅ ) = 0
P(A) = 1 − P(A)
P(A ∪ B) = P(A) + P(B) − P(A ∩ B)
P(A ∩ B)
P(A | B) =
für P(B) ≠ 0
P(B)
A und B stochastisch unabhängig:
P(A | B) = P(A);
P(A ∩ B) = P(A)P(B)
-2-
Formelsammlung zur Klausur Induktive Statistik
Prof. Dr. Nikolaus
Wolik
3. Zufallsvariable
Diskrete Zufallsvariable:
P(X = xi ) = pi falls x=xi
Wahrscheinlichkeitsfunktion f(x) = 
0
sonst

∑ f(xi )
Verteilungsfunktion F(x) = P(X ≤ x) =
xi ≤ x
Erwartungswert E(X) = µ = ∑ xipi
Varianz V(X) = σ2 = ∑ (xi − µ)2 pi
Stetige Zufallsvariable:
b
Dichtefunktion und Wahrscheinlichkeit
P(a ≤ X ≤ b) = ∫ f(x)dx
a
P(X = x) = 0
x
Verteilungsfunktion F(x) = P(X ≤ x) =
∫ f(t)dt
−∞
Erwartungswert E(X) = µ =
+∞
∫ xf(x)dx
−∞
Varianz V(X) = σ2 =
+∞
∫ (x − µ)
2
f(x)dx
−∞
4. Verteilungen
Binomialverteilung:
n
f(n,k,p) =   pk (1 − p)n−k
k 
µ = np; σ = np(1 − p)
Poissonverteilung: (approximativ für kleine p und große n, Verteilung seltener Ereignisse)
f(n,k,p) =
(np)k
k!enp
µ = np; σ = np
Hypergeometrische Verteilung
 M  N − M
 

x  n − x 

f(x,n,M,N) =
 N
 
n
-3-
Formelsammlung zur Klausur Induktive Statistik
Normalverteilung:
Prof. Dr. Nikolaus
Wolik
X ∼ N(µ, σ) :
Dichtefunktion f(x) =
1
σ 2π
Verteilungsfunktion F(x) =
E(X)=µ
1 x −µ 2
− (
)
σ
2
e
x
1
∫
σ 2π −∞
e
1 t −µ 2
− (
)
2 σ dt
Var(X)=σ2
Standardisierte NV: Ist X ∼ N(µ, σ) , dann ist Z :=
Dichtefunktion f(z) =
1
2π
e
X−µ
Standardnormalverteilt: Z ∼ N(0,1)
σ
1
− z2
2
Verteilungsfunktion F(z) = Φ(z) =
1
z
∫
2π −∞
1
− t2
2
e dt
a−µ
b−µ
≤Z≤
) = Φ(z 2 ) − Φ(z1 )
σ
σ
a−µ
b−µ
mit z1 =
und z 2 =
σ
σ
P(a ≤ X ≤ b) = P(
Eine Tabelle für Φ(z) (z-Tabelle) wird zur Klausur ausgeteilt!!
5. Grenzwertsätze
1.)
Ist X binomialverteilt nach f(n,k,p) dann ist Z :=
X − np
np(1 − p)
für hinreichend große
n standardnormalverteilt.
Dies gilt ebenso für Z :=
2.)
X−p
p(1 − p)
n
mit X =
X
.
n
Gegeben sind n unabhängige und identisch verteilte Zufallsvariablen X1,…, Xn
mit Erwartungswert µ und Standardabweichung σ. Dann kann ihre Summe
n
Sn = ∑ Xi und ihr arithmetisches Mittel X =
i=1
Sn
für hinreichend großes n durch
n
die Normalverteilung aproximiert werden:
P(Sn ≤ s) ≈ Φ(
s − nµ
)
σ n
x −µ .
P(X ≤ x) ≈ Φ(
)
σ
n