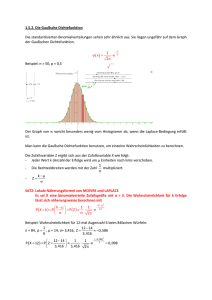
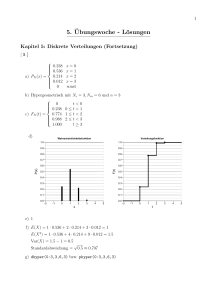
Wiederholungstest: Grundlagen der Statistik

Wiederholungstest: Grundlagen der Statistik
Multiple Choice Quiz: Klicken Sie die richtige Lösung!
1. Die bedingte Wahrscheinlichkeit P (A|B) ist definiert als . . .
(A ∩ B ist der Durchschnitt und A ∪ B die Vereinigung zweier Mengen A, B)
(a) P P(A∩B)
(B)
(e) KdvAir1
(b)
P (A∪B)
P (B)
(c)
P (A∩B)
P (A)P (B)
(d)
P (A∩B)
P (B∪B)
2. Sei x eine stetige Zufallsvariable und f (x) die Dichtefunktion, dann ist der Erwartungswert
definiert
R∞
R∞
R∞
Rx
(a) −∞ x dx
(b) −∞ f (x) dx
(c) −∞ xf (x) dx
(d) −∞ f (v) dv
(e) KdvAir1
3. Die Varianz einer Zufallsvariable y ist definiert als . . .
P
P
(c) E[y − E(y)]2
(a) i yf (y)
(b) N1 i yf (y)
(e) KdvAir1
(d)
1
N −2
P
i
yi2
4. Zwei Zufallsvariablen x und y sind statistisch unabhängig, wenn . . .
(a) Cov(x, y) = 0
(b) E(xy) = 0
(c) E(x|y) = f (x, y) (d) f (x, y) = f (x)f (y)
(e) KdvAir1
5. Sei x eine Zufallsvariable mit x ∼ iid(µ, σ 2 ), dann ist der Erwartungswert E(2 + 4x) gleich
...
(a) µ
(b) 4µ
(c) 16µ
(d) 2 + 4µ
(e) KdvAir1
6. Sei x eine Zufallsvariable mit x ∼ iid(µ, σ 2 ), dann ist Var(2 + 4x) gleich . . .
(a) 4 + 16Var(x)
(b) 4 + 16Var(x2 )
(c) 16Var(x)
(d) 4σ 2
1
(e) KdvAir
7. Eine Verteilungsfunktion . . .
(a) gibt an, wie die einzelnen Elemente einer Zufallsvariable verteilt sind.
(b) ist das Analogon zu einer Dichtefunktion für den diskreten Fall.
(c) ist das Analogon zu einer Dichtefunktion für den stetigen Fall.
(d) ist die kumulierte Dichtefunktion.
Wird erweitert . . .
1
KdvAir . . . Keine der vorhergehenden Antwortmöglichkeiten ist richtig.