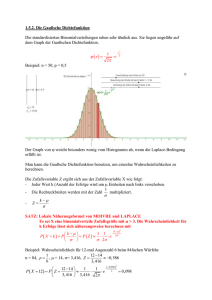
1.5.2. Die Gaußsche Dichtefunktion Die standardisierten

1.5.2. Die Gaußsche Dichtefunktion
Die standardisierten Binomialverteilungen sehen sehr ähnlich aus. Sie liegen ungefähr auf dem Graph
der Gaußschen Dichtefunktion.
2
ϕ ( x )=
Beispiel: n = 50, p = 0,5
x
−
1
⋅e 2
2π
Der Graph von w weicht besonders wenig vom Histogramm ab, wenn die Laplace-Bedingung erfüllt
ist.
Man kann die Gaußsche Dichtefunktion benutzen, um einzelne Wahrscheinlichkeiten zu berechnen.
Die Zufallsvariable Z ergibt sich aus der Zufallsvariable X wie folgt:
- Jeder Wert k (Anzahl der Erfolge wird um µ Einheiten nach links verschoben.
1
- Die Rechteckbreiten werden mit der Zahl
multipliziert.
σ
k −µ
- Z=
σ
SATZ: Lokale Näherungsformel von MOIVRE und LAPLACE
Es sei X eine binomialverteile Zufallsgröße mit σ > 3. Die Wahrscheinlichkeit für k Erfolge
lässt sich näherungsweise berechnen mit
−
1 1
k −µ 
P(X = k) = P
⋅e
 = P(Z) ≈ ⋅
σ 2π
 σ 
(k −µ )2
2 σ2
Beispiel: Wahrscheinlichkeit für 12-mal Augenzahl 6 beim 84fachen Würfeln:
1
12 − 14
n = 84, p = , µ = 14, σ= 3,416,
=
Z
≈ −0,586
3,416
6
−
12 − 14 
1
1

≈
⋅
⋅e
P ( X =12 ) =P  Z =

3,416  3,416 2π

( −0,586 )2
2
=0,098