Bernoulli Versuche

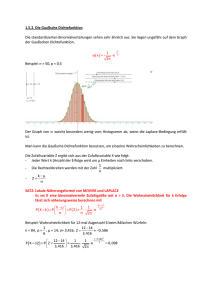
Bernoulli Versuche
Definition:
Ein einstufiger BV ist ein Zufallsversuch mit zwei möglichen Ergebnissen die man mit
Erfolg und Misserfolg bezeichnet.
Wird ein BV n-mal durchgeführt und ändert sich die W. p für Erfolg nicht, so spricht man
von einem n-stufigen BV.
Definition der Binomialverteilung:
Gegeben sei ein n-stufiger BV mit der Erfolgsw. p und der Misserfolgsw. q = 1-p .
Die Wahrscheinlichkeitsverteilung der Zufallsgröße
X: Anzahl der Erfolge
heißt Binomialverteilung.
HL
HLJN HL
H
L
H
L
J
N
H
L
H
L
JNHL
H
LHLHL
H
L
Die Wahrscheinlichkeit für k Erfolge berechnet man mit der Formel:
n
* pk *
k
P X= k =
1- p
n- k
Erwartungswert:
Ist X die Anzahl der Erfolge bei einem n-stufigen BV mit der Erfolgsw. p, dann gilt
E x = n* p
Beweis für n = 1:
P X= k
k
1
0
* p0 * 1 - p
0
1
* p1 * 1 - p
1
1
®
1
= 1- p
0
=p
E x = 0* 1 - p + 1* p = 1* p = n* p
Varianz
X sei binomialverteilt zu den Parametern n und p.
Dann gilt:
V x = n* p* q
® Standartabweichung s =
H
L
n+ p + q
Gaußsche Dichtefunktion
Der Graph der Funktion mit dem Term
j
x =
1
IM
1 2
x
* e 2
2p
heißt Gaußsche Dichtefunktion.
Lokale Näherungsformel von Moivre und Laplace
Für große n gilt:
Wenn X zu n und p binomialverteilt ist gilt:
HL JN
P X= k »
1
s
* j
k- m
s
Diese Näherung liefert brauchbare Werte für σ > 3
Integrale Näherungsformel von Moivre und Laplace
φ sie eine Stammfunktion der Gaußschen Dichtefunktion ϕ.
X sei B(n, p).
Dann gilt bei großen n:
H LàJJ NNH
L J NJ N
b- m+0,5
P a£ X£ b »
s
a- m- 0,5
j
x âx = f
b - m+ 0, 5
s
s
a - m- 0, 5
- f
s
Diese Näherung liefert brauchbare Werte für σ > 3
H
ÈÈL J N
H
ÈÈL H
L
Wahrscheinlichkeiten in der n-fachen σ-Umgebung
Für einen BV mit B(n, p) gilt:
P
X- m £ z* s = 2 * f z+
1
2s
Für n >> 1 und daraus resultierendes σ >> 3 gilt daher:
P
X- m £ z* s = 2 * f z
wichtige Werte:
Radius der Umgebung
1,645 σ
1,96 σ
2,575 σ
Näherungswert von P(x=k)
0,90
0,95
0,99
H
ÈÈLJ
H NLJ N
J
N
J
N
JJNN
JN
HL H
L
Beweis:
P
x - m £ z * s = P m- z * s £ X £ m+ z * s
m+ z * s - m+ 0, 5
=f
=f
- f
s
z* s
s
+
0, 5
s
- f
- z* s
1
1
= f z+
- f - z2s
2s
1
= 2* f z +
- 1
2s
H
ÈÈL H
L
s
m- z * s - m+ - 0, 5
s
+
0, 5
s
da f - z = 1 - f z
1
da der Term 2 s für n >>1 sehr gering wird, kann er vernachlässigt werden.
® P
x - m £ z * s = 2* f z - 1