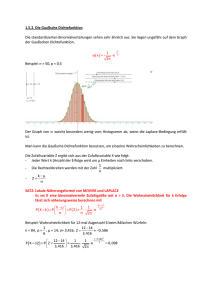
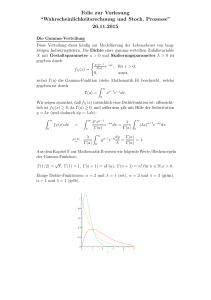
WAHRSCHEINLICHKEITSRECHNUNG - ¨UBUNG 4. 1.) Bei einer

WAHRSCHEINLICHKEITSRECHNUNG - ÜBUNG 4.
1.) Bei einer Geschwindigkeitsmessung an einem Straßenquerschnitt wurden
folgende Geschwindigkeiten ( km
h ) beobachtet:
51, 52, 57, 58, 61, 63, 65, 68, 69, 70.5, 71, 71, 72.5, 73, 73, 73.5, 74, 75, 75,
77, 78, 78, 78, 79, 80.5, 80.5, 82, 82, 82, 82.5, 83, 84, 85, 85, 85, 87, 87.5,
88, 88.5, 88.5, 89.5, 89.5, 89.5, 91, 91, 93, 95, 95, 97, 98, 99, 99, 99, 99.5,
103, 103.5, 108, 110, 115, 116, 122
(Diese Zahlen sind die Werte von X.)
min xi =?, max xi =?
W (X) ⊂ [50, 130] := I
Teilen Sie das Intervall I in 8 Teilintervalle der Länge 10 und füllen sie die
Folgende Tabelle:
Skizzieren Sie f und F !
Table 1. My caption
Nummer
Geschwindigkeits- Intervallmittelpunkt
der Klasse k
intervall
(ui )
absolute
Häufigkeit
(ak )
Wahrscheinlichkeit
(relative Häufigkeit) F(x)
(hk ∼ f (ui )
Berechnen Sie: E(X), V ar(X), σ, v!
P (60 < X < 70) =?, P (X ≤ 80) =?, P (X ≥ 70) =?
2.) Sei X eine stetige Zufallsgröße mit der Dichtefunktion
f (x) =
  α β α+1
, x ≥ β(α > 0, β > 0)
0
,sonst
β
x
a)
b)
c)
d)
3.)
Man beweise, daß f eine Dichtefunktion ist!
Geben Sie F an!
Falls α > 0, dann berechne E(X), V ar(X)!
Sei α = 3, β = 4! Geben Sie P (5 < X < 7), P (X ≥ 10), E(X),
V ar(X), σ, v!
a
, a =?, E(X) =?
a) xk = k, P (X = k) = (k+1)!
P∞
k+1
b) xk = (−1)
(2k + 1), P (X = k) = k21+k , Zeigen Sie, daß k=1 =
1, E(X) =?
1
2
WAHRSCHEINLICHKEITSRECHNUNG - ÜBUNG 4.
4.) Eine Diskrete Zufallsgröße besitzt die Verteilungsfunktion:

0
,für x < 1



0, 3 ,für 1 ≤ x < 2
F (x) =

0, 5 ,für 2 ≤ x < 3



1
,für x ≥ 3
Man bestimme:
a) W (X), f
b) E(X)
c) V ar(X), σ, v
d) P (x ≥ 1, 8)
5.)
(
f (x) =
0
x<0
2
a e
−x2 a
2
x
x≥0
a) a =?
b) Zeichnen Sie
f und F !
c) P X ≤ 12 =?, P (X ≥ 1) =?, P (−1 ≤ X ≤ 1) =?
xi
-2
-1
f (xi ) 0,15 0, 3p
1
3
0,1 p2
4
0,05
6.)
a) p =?
b) F (X) =?
c) E(X) =?
d) V ar(X) =?, σ =?, v =?
e) P (0 ≤ X < 2, 8) =?
7.) Für welche Werte a und b ist
a) F (x) := a + b arctan x, x ∈ R eine Verteilungsfunktion?
b) f =? Zeichnen Sie f und F !
c) P (X ≤ 1) =?, P (X ≥ 2) =?, P − π4 < X ≤ π4 =?
8.) *
fc sei eine Dichtefunktion von X
B
h
A
c
c+2
c+4
c+8
a) h =?
b) Fc =?
c) * Bei welchem Parameter ”‘c”’ ist die Wahrscheinlichkeit dafür, daß
eine Realisation von X im Intervall [7, 5; 10] liegt, am größten?