Folie zur Vorlesung - Mathematics TU Graz

Folie zur Vorlesung
“Wahrscheinlichkeitsrechnung und Stoch. Prozesse”
26.11.2015
Die Gamma-Verteilung
Diese Verteilung dient häufig zur Modellierung der Lebensdauer von langlebigen Industriegüstern. Die Dichte einer gamma-verteilten Zufallsvariable
X mit Gestaltsparameter a > 0 und Skalierungsparameter λ > 0 ist
gegeben durch
( a a−1
λ x
e−λx , für x > 0,
Γ(a)
fX (x) =
0,
sonst,
wobei Γ(a) die Gamma-Funktion (siehe Mathematik B) beschreibt, welche
gegeben ist durch
Z
∞
xa−1 e−x dx.
Γ(a) =
0
Wir zeigen zunächst, daß fX (x) tatsächlich eine Dichtefunktion ist: offensichtlich ist fX (x) ≥ 0, da Γ(a) ≥ 0, und außerdem gilt mit Hilfe der Substitution
y = λx (und dadurch dy = λ dx):
Z ∞
Z ∞ a a−1
Z ∞
λ x
λ
−λx
fX (x) dx =
(λx)a−1 e−λx dx
e dx =
Γ(a)
Γ(a)
0
0
0
y=λx
=
λ
Γ(a)
Z
0
∞
y a−1 e−y
dy
Γ(a)
=
= 1.
λ
Γ(a)
Aus dem Kapitel F zur Mathematik B wissen wir folgende Werte/Rechenregeln
der Gamma-Funktion:
√
Γ(1/2) = π, Γ(1) = 1, Γ(a + 1) = aΓ(a), Γ(n + 1) = n! für n ∈ N, a > 0.
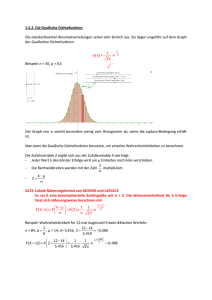
Einige Dichte-Funktionen: α = 2 und λ = 1 (rot), α = 2 und λ = 3 (grün),
α = 1 und λ = 1 (gelb).
Der Erwartungswert einer gamma-verteilten Zufallsvariablen X ergibt sich
wieder mit Hilfe der der Substitution y = λx (und dadurch dy = λ dx):
Z ∞
Z ∞
Z ∞ a a
(λx)a −λx
λ x −λx
e dx =
e dx
EX =
xfX (x) dx =
Γ(a)
Γ(a)
0
0
0
y=λx
=
1
Γ(a)
Z
∞
y a e−λx
0
dy
Γ(a + 1)
aΓ(a)
a
=
=
= .
λ
λΓ(a)
λΓ(a)
λ
Das zweite Moment ergibt sich mit derselben Substitution nach einer partiellen Integration wie folgt:
Z ∞
Z ∞ a
λ
2
2
E(X ) =
x fX (x) dx =
xa+1 e−λx dx
Γ(a) |{z} |{z}′
0
0
=:f
=
Z ∞ a
λa a+1 −1 −λx ∞
λ
−1 −λx
x
e −
(a + 1)xa
e
dx
|{z}
Γ(a)
Γ(a) | {z } |λ {z }
0
|λ {z } 0
=f
=
y=λx
=
=
=:g
|
=f ′
=:g
{z
}
=0−0=0
a+1
λΓ(a)
Z
∞
a+1
λΓ(a)
Z
∞
(λx)a e−λx dx
0
y ae−y
0
dy
λ
a+1
a2 + a
a+1
Γ(a
+
1)
=
aΓ(a)
=
.
λ2 Γ(a)
λ2 Γ(a)
λ2
Somit ergibt sich die Varianz als
Var(X) = E(X 2 ) − E(X)
2
=
a
a2 + a a2
− 2 = 2.
2
λ
λ
λ
=:g
Weitere Bemerkungen:
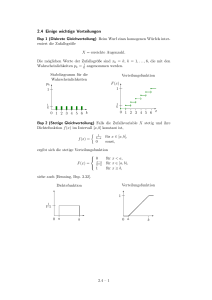
• Eine integralfreie Darstellung der Verteilungsfunktion
Z x
Z x a a−1
λ t
e−λt dt
FX (x) =
fX (t)dt =
Γ(a)
0
0
existiert nur für a ∈ N.
• Im Spezialfall a = 1 wird die Dichtefunktion wegen Γ(1) = 1 zu
(
λe−λx , für x > 0,
fX (x) =
0,
sonst
D.h. die Gamma-Verteilung mit a = 1 ist genau die Exponentialverteilung mit Parameter λ > 0.
• Sei X gamma-verteilt mit den Parametern a > 0 und λ > 0. Betrachte
nun die Zufallsvariable
Z = λX.
Dann erhalten wir für die Verteilungsfunktion von Z:
FZ (z) = P[Z ≤ z] = P[λX ≤ z] = P[X ≤ z/λ] = FX (x/λ).
Daraus ergibt sich die Dichtefunktion von Z für z > 0 als
∂
∂
z 1
z
= fX
·
FZ (z) =
FX
∂z
∂z
λ
λ
λ
a−1
λa λz
z
1
e−λ λ ·
=
Γ(a)
λ
fZ (z) =
z a−1 −z
e .
=
Γ(a)
D.h. Z = λX ist wiederum eine Gamma-Verteilung mit den Parametern a und λ = 1.
Grenzwertsatz von De Moivre-Laplace:
Sei X binomialverteilt mit den Parametern n und p, d.h.
n k
p (1 − p)n−k für k ∈ {0, 1, . . . , k}.
P[X = k] =
k
Dann kann man für ausreichend großes n ∈ N folgende Approximationen
machen: (Faustregel: n min{p, 1 − p} > 5)
1. Für k ∈ {0, 1, . . . , n}:
(k−np)2
1
P[X = k] ≈ p
e− 2np(1−p) = ϕ(k),
2πnp(1 − p)
wobei
ϕ die Dichte einer Normalverteilung mit µ = np und σ =
p
np(1 − p) ist.
2. Für k, l ∈ {0, 1, . . . , n} mit l ≤ k:
l − 1 − np k + 1 − np 2
−Φ p 2
,
P[l ≤ X ≤ k] ≈ Φ p
np(1 − p)
np(1 − p)
wobei Φ die Verteilungsfunktion der Standardnormalverteilung ist.
Die Terme ± 21 werden Stetigkeitskorrektur genannt (siehe Tafel!).
Beispiel: Ein spielsüchtiger Spieler setzt bei 2000 Roulette-Spielen stets auf
Rot. Wie groß ist die Wahrscheinlichkeit, daß er zwischen 980 und 1020
mal gewinnt? Man berechne die Wahrscheinlichkeit approximativ über die
Normalverteilung!