Aufgabe 1 Aufgabe 2

Aufgabe 1
Seien fX die Dichte und FX die Verteilungsfunktion von X. Für die Verteilungsfunktion FY von Y gilt
FY (x) = P[Y ≤ x] = P[αX + β ≤ x] = P[X ≤
x−β
α ]
= FX ( x−β
α )
(x ∈ R)
Damit gilt für die Dichte fY von Y
d
d
1
x−β
FY (x) =
FX ( x−β
α ) = α fX ( α )
dx
dx
x−β
2
1
1
1
(
−µ)2
exp − α2σ2
=p
exp − (x−(αµ+β))
= √
2
2(ασ)
α 2πσ 2
2π(ασ)2
fY (x) =
Folglich ist Y normalverteilt zu den Parametern (αµ + β, ασ).
Aufgabe 2
Es bezeichne Φ die Verteilungsfunktion der Standard-Normalverteilung. Sei X
normalverteilt zu den Parametern (µ, σ), dann ist X−µ
standard-normalverteilt
σ
(Aufgabe 8.1); damit gilt für die Verteilungsfunktion FX von X
FX (x) = P[X ≤ x] = P[ X−µ
≤
σ
x−µ
σ ]
= Φ( x−µ
σ )
Ferner gilt Φ(−x) = 1 − Φ(x) für alle x ∈ R.
Sei n die Anzahl der verkauften Tickets und Xn die Anzahl der Passagiere,
die den Flug antreten. Nehmen wir an, dass alle Passagiere den Flug unabhängig
voneinander mit einer Wahrscheinlichkeit von 0.7 antreten, so ist Xn binomialverteilt zu den Parametern p = 0.7 und n. Nach dem Satz von de MoivreLaplace können wir die Verteilung durch eine Normalverteilung zu den Parametern µn = E[Xn ] = np und σn2 = Var(Xn ) = np(1 − p) approximieren. Somit
erhalten wir für α ∈ (0, 1)
P[Xn ≤ 100] = Φ( 70−µ
σ )≥α
p
−1
⇔ np + Φ (α) np(1 − p) ≤ 100
p
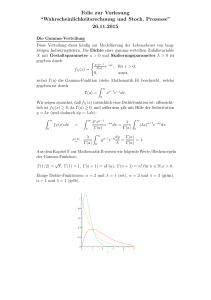
Ein Plot der Funktionen n 7→ np+Φ−1 (α) np(1 − p) für α ∈ {0.9, 0.95, 0.99}
zeigt, dass maximal


133 falls α = 0.9
n = 130 falls α = 0.95


125 falls α = 0.99
verkauft werden dürfen. (Man liest aus der Tabelle der Normalverteilung jeweils
den zu α nächsten Wert, z.B. ist das bei α = 0.9 der Wert 0.915 und damit
Φ−1 (0.915) = 1.29)
1
106
alpha = 0.9
104
102
alpha = 0.95
100
alpha = 0.99
98
96
125 126 127 128 129 130 131 132 133 134 135
n
Aufgabe 3
Bemerke außerdem, dass P[X ≤ x] = P[X < x] für absolutstetige Zufallsvariablen X. Es gilt nun
P[|X − µ| < 1] = 0.95
⇔ P[− σ1 <
⇔ Φ( σ1 ) −
X−µ
< σ1 ] = 0.95
σ
Φ(− σ1 ) = 0.95
⇔ 2Φ( σ1 ) − 1 = 0.95
⇔ σ=
1
Φ−1 (0.975)
Aufgabe 4
a) Die Ausschussquote ist gegeben durch
P[D < d1 ] + P[D > d2 ] = Φ
d1 +d2
2
d2 −d1
4
d1 −
!
+
1−Φ
d1 +d2
2
d2 −d1
4
d2 −
!!
= 1 + Φ(−2) − Φ(2)
= 2 − 2Φ(2)
≈ 0.046
b) Wir nehmen an, dass die Kugelgrößen unabhängig voneinander sind, dann
ist die Anzahl der Ausschussteile binomialverteilt mit Parametern p =
0.046 und n = 100. Somit gilt
P[X ≥ 3] = 1 −
2 X
n
k
k=0
2
pk (1 − p)n−k ≈ 0.839
Verwenden wir die Poissonverteilung zum Parameter λ = np = 4.6 als
Approximation, so erhalten wir
P[X ≥ 3] = 1 −
2
X
λk
k=0
k!
e−λ ≈ 0.832
Die Poissonverteilung liefert also ein ziemlich gute Approximation.
3