Stochastik

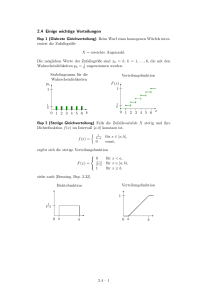
Formelsammlung
Stochastik
P( E ) :=
k
Anzahl der 'günstigen' Fälle
==
.
n
Anzahl der möglichen Fälle
Additionssatz
Seien A und B zwei beliebige Ereignisse. Dann gilt
P ( A ∪ B ) = P ( A) + P ( B ) − P ( A ∩ B )
Bedingte Wahrscheinlichkeit
 P ( A ∩ B)
, falls

P ( A / B ) :=  P ( B )
 0,
falls

P(B) > 0
P(B) = 0
Multiplikationssatz für beliebige Ereignisse
P( A ∩ B) = P( B) ⋅ P( A / B)
Spezialfall: unabhängige Ereignisse
P ( A ∩ B ) = P ( A) ⋅ P ( B )
Seien E i , i = 1, 2, ..., n , unabhängige Ereignisse.
Dann gilt:
n
n

P  ∪ E i  = 1 − ∏ (1 − P ( E i ) ) .
i =1
 i =1 
Totale Wahrscheinlichkeit:
n
P ( A) = ∑ P ( A / B i ) ⋅ P ( B i )
i =1
Bayes
P (B i / A ) =
P ( A / B i ) ⋅ P (B i )
∑ P ( A / B i ) ⋅ P (B i )
n
i = 1, 2, ..., n .
,
i =1
1
Auswahlschemata
1. ohne Zurücklegen:
Pohne Zurücklegent
M
m
=
 N −M 
 ⋅

  n−m 
N
 
n
2. mit Zurücklegen
n
Pmit Zurücklegen =   ⋅ p m ⋅ q n − m ,
m
M
=: p ,
N
q := 1 − p
Verteilungsfunktion
0
 k

F ( x ) = P ( X < x ) =  ∑ pi
 i =1
1
for
x ≤ x1
for
x k < x ≤ x k +1 , k = 1, 2, ...,n − 1
for
x > xn
Einige Eigenschaften der Verteilungsfunktion F ( x ) :
1.
0 ≤ F ( x ) ≤ 1, ∀ x ∈ R 1 .
2.
∀x1 , x 2 : x1 < x 2 ⇒ F ( x1 ) ≤ F ( x 2 ) .
3.
∀x1 , x 2 : x1 < x 2 ⇒ P ( x1 ≤ X < x 2 ) = F ( x 2 ) − F ( x1 ) .
4.
x → −∞
x → +∞
⇒
⇒
F ( x) → 0
F ( x) → 1 .
5.
F (x) ist mindestens linksseitig stetig und hat eine endliche Anzahl von Sprungstellen.
Wahrscheinlichkeitsfunktion
xi
x1
x2
…
xn
pi = P ( X = xi ) = f ( xi )
p1
p2
…
pn
2
Dichtefunktion
Sei F ( x ) eine differenzierbare Verteilungsfunktion einer stetigen Zufallsvariable X . Die
Funktion
f ( x ) := F ' ( x )
heißt die Dichtefunktion von X .
Wichtige Eigenschaften einer Dichtefunktion
1.
F ( x) = P( X < x)
= P ( −∞ < X < x )
x
= ∫ f (t ) dt .
−∞
2.
P ( a ≤ X < b ) = F (b ) − F ( a )
b
= ∫ f ( x ) dx .
a
3.
+∞
P ( −∞ < X < +∞ ) = ∫ f ( x ) dx = 1 .
−∞
Erwartungswert
Als Erwartungswert einer Zufallsgröße X bezeichnet man:
∞
 ∑ xi ⋅ pi
 i =1
E ( X ) :=  + ∞
 x ⋅ f ( x ) dx
∫
 −∞
falls X diskret
falls X stetig
Varianz bzw. Dispersion
∞
2
 ∑ ( xi − E ( X ) ) ⋅ p i
 i =1
D 2 ( X ) :=  + ∞
 ( x − E ( X ) )2 ⋅ f ( x ) dx
 .∫∞
falls X : discrete
falls X : stetig
bzw.
2
∞ 2
 ∞

 ∑ xi ⋅ pi −  ∑ xi ⋅ pi  ,
 i =1

 i =1
2
D ( X ) :=  + ∞
+∞

 2

2
 ∫ x ⋅ f ( x ) dx −  ∫ x ⋅ f ( x )  ,
 −∞

 .∞
3
falls X diskret
falls X stetig
Standardabweichung
D( x ) > 0
Hypergeometrische Verteilung
M
x
P ( X = x ) = pi = 
 N −M
⋅
 n − x
N
n 
 


,
x = 0,1,..., n;
n≤M ≤N.
E (X ) = n⋅ p
D2( X ) =
N −n
n⋅ p⋅q
N −1
Binomialverteilung
n
P ( X = x ) = pi =   ⋅ p x ⋅ q n − x , x = 0, 1,..., n .
 x
E (X ) = n⋅ p ,
D2 ( X ) = n ⋅ p ⋅ q .
“Gilt 10 ⋅ n ≤ N , so kann die hypergeometrische Verteilung durch die Binomialverteilung
approximiert werden.“
Poisson-Verteilung
P ( X = x) =
λx
x!
⋅ e − λ , x = 0,1,..., n .
E ( X ) = D2(X ) = n ⋅ p = λ .
“Für
n ⋅ p ≤ 10
und
n ≥ 1500 p ,
kann die Binomialverteilung durch die Poisson-Verteilung approximiert werden.“
Normalverteilung
Eine stetige Zufallsgröße X sei als normalverteilt bezeichnet, wenn sie folgende
Wahrscheinlichkeitsdichte besitzt:
f ( x; µ ,σ ) =
x−µ
⋅ϕ 

σ
 σ 
1
4
−
1
= ⋅
e
σ
2π
1
( x − µ )2
2σ 2
,
x ∈ R1
Eine normalverteilte Zufallsgröße X hat die Verteilungsfunktion
x−µ
F ( x; µ , σ ) = Φ 

 σ 
x−µ
=
1
2π
=
σ
1
2π
E (X ) = µ ,
∫
e
−
t2
2
dt
−∞
x
∫e
−
( t − µ )2
2σ 2
x ∈ R1 .
dt ,
−∞
D2 ( X ) = σ 2 .
Standardisierte Normalverteilung
Wegen
X −µ
Z=
mit E ( Z ) = 0,
σ
D2 (Z ) = 1
erhält man folgende Funktionen:
1. Die Dichtefunktion der standardisierten Normalverteilung:
2
x
−
1
e 2,
2π
f ( x) = ϕ ( x ) =
x ∈ R1 .
2. Die standardisierte Verteilungsfunktion der Normalverteilung:
F ( x) = Φ ( x )
=
1
2π
x
∫
e
−
t2
2
dt ,
x ∈ R1 .
−∞
ϕ ( − x ; 0, 1) = ϕ ( x ; 0, 1) ,
Φ ( − x ; 0, 1) = 1 − Φ ( x ; 0, 1) .
c
P ( X − µ < c) = 2 ⋅ Φ 
σ

1
 − 1, c ∈ R .

5
Dreisigmaregel
P ( X − µ < σ ) = 0.6828
P ( X − µ < 2σ ) = 0.9544
P ( X − µ < 3σ ) = 0.9972 .
Dies bedeutet:
Etwa 68% aller Beobachtungswerte liegen im Intervall [ µ − σ , µ + σ ] :
Etwa 95% aller Beobachtungswerte liegen im Intervall [ µ − 2σ , µ + 2σ ] :
Etwa 99.7% aller Beobachtungswerte liegen im Intervall [ µ − 3σ , µ + 3σ ] :
6