Stetige Zufallsvariable Beispiel: Eine Füllanlage für Wein, die 0,75ℓ

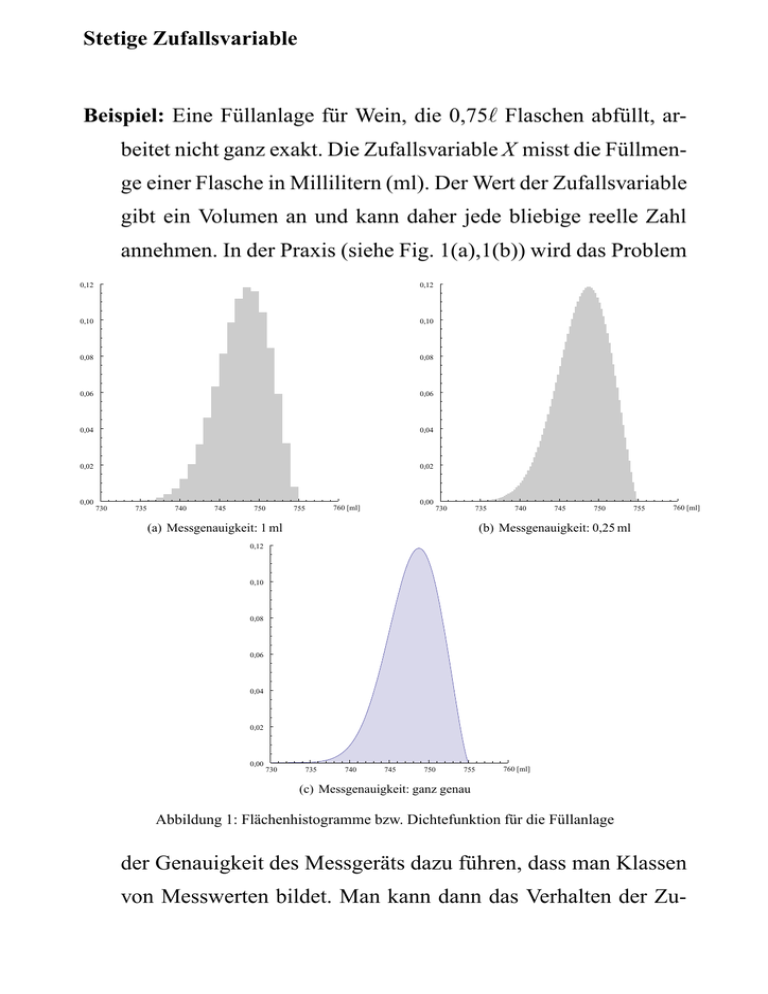
Stetige Zufallsvariable
Beispiel: Eine Füllanlage für Wein, die 0,75ℓ Flaschen abfüllt, arbeitet nicht ganz exakt. Die Zufallsvariable X misst die Füllmenge einer Flasche in Millilitern (ml). Der Wert der Zufallsvariable
gibt ein Volumen an und kann daher jede bliebige reelle Zahl
annehmen. In der Praxis (siehe Fig. 1(a),1(b)) wird das Problem
0,12
0,12
0,10
0,10
0,08
0,08
0,06
0,06
0,04
0,04
0,02
0,02
0,00
730
735
740
745
750
755
0,00
760 [ml]
730
735
(a) Messgenauigkeit: 1 ml
740
745
750
755
760 [ml]
(b) Messgenauigkeit: 0,25 ml
0,12
0,10
0,08
0,06
0,04
0,02
0,00
730
735
740
745
750
755
760 [ml]
(c) Messgenauigkeit: ganz genau
Abbildung 1: Flächenhistogramme bzw. Dichtefunktion für die Füllanlage
der Genauigkeit des Messgeräts dazu führen, dass man Klassen
von Messwerten bildet. Man kann dann das Verhalten der Zu-
fallsvariable durch ein Flächenhistogramm darstellen. Wird die
Messgenauigkeit immer besser, so verschwinden die Balkenstufen und es entsteht eine glatte Kurve. (Fig. 1(c)).
Man nennt diese Funktion Dichtefunktion der Zufallsvariable X.
Interpretation bzw. Eigenschaften:
Flächenhistogramm
Dichtefunktion
0,12
0,12
0,10
0,10
0,08
0,08
0,06
0,06
0,04
0,04
0,02
0,02
Gesamtfläche:
Berechnung der
Gesamtfläche:
Flächenstück,
das P(745 < X ≤ 750)
repräsentiert
0,00730
735
740
745
750
755
760 [ml]
0,00730
Berechnung von
P(745 < X ≤ 750)
Jede Funktion f (x) mit den Eigenschaften:
•
Z∞
f (x)dx =
und
−∞
•
f (x) ≥
∀x∈R
ist Dichtefunktion einer stetigen Zufallsvariable.
735
740
745
750
755
760 [ml]
Ist f (x) Dichtefunktion der Zufallsvariable X, dann heißt die Funktion
F(x) =
Zx
f (x)dx
−∞
Verteilungsfunktion der Zufallsvariable X. Jede Verteilungsfunktion
einer Zufallsvariable X hat die folgenden Eigenschaften:
•
•
•
F(x) ≥
lim F(x) =
x→−∞
lim F(x) =
x→∞
F(x) ist monoton
• Typischer Graph:
Vergleich diskrete bzw. stetige Zufallsvariable:
Wahrscheinlichkeit für
einen bestimmten Wert
P(X ≤ b) =
P(a < X ≤ b) =
Erwartungswert
Varianz
oder
diskrete Zufallsvar.
stetige Zufallsvariable
P(X = xi) =
P(X = c) =
Beispiel 1:
Die Dichtefunktion y = f (x) für die Lebensdauer x von Batterien eines bestimmten Typs sei durch folgenden Graphen gegeben:
f
h
1
-
1
2
3
4
5
x
(a) Bestimmen Sie h so, dass f (x) eine Dichtefunktion ist!
(b) Geben Sie den Funktionsterm von f als stückweise lineare Funktion an:


...
für




f (x) =
...
für





0
sonst
(c) Wie groß ist die Wahrscheinlichkeit, dass eine Batterie länger als zwei
Jahre funktioniert?
(d) Wie groß ist die Wahrscheinlichkeit, dass eine Batterie weniger als 3
Jahre funktioniert?
(e) Wie groß ist die Wahrscheinlichkeit, dass die Lebensdauer einer Batterie
zwischen 1,5 und 2 Jahren liegt?
(f) Man weiß von einer bestimmten Batterie, dass sie genau 1 Jahr lang
in Betrieb war. Wie groß ist nun die Wahrscheinlichkeit, dass sie noch
mindestens 1 weiteres Jahr funktionieren wird?
(g) Bestimmen Sie den Erwartungswert µ der Lebensdauer (mittlere Lebensdauer) der Batterien!
(h) Berechnen Sie die Varianz σ 2 für die Lebensdauer der Batterien!
(i) Berechnen Sie den Term der Verteilungsfunktion!
Beispiel 2:
Die Lebensdauer von bestimmten Viren sei für die Zeit t > 0 (in Jahren)
durch die Dichtefunktion
(
1
C · e− 2 t für
t >0
f (t) =
0
sonst
gegeben. (Die meisten dieser Viren zerfallen sofort; wenige können sogar
unendlich lange existieren.)
(a) Bestimmen Sie die Konstante C so, dass f (t) eine Dichtefunktion darstellt!
(b) Skizzieren Sie den Graph der Dichtefunktion!
(c) Bestimmen Sie Funktionsterm und Graph der Verteilungsfunktion!
(d) Wie groß ist die Wahrscheinlichkeit, dass
i. ein solches Virus genau 2 Jahre existiert?
ii. ein solches Virus höchstens 2 Jahre existiert?
iii. ein solches Virus länger als 3 Jahre existiert?
iv. die Lebensdauer eines solchen Virus zwischen 1 und 3 Jahren beträgt?
v. ein zweijähriges Virus noch mindestens ein Jahr weiter existiert?
(e) Wie groß ist die „Lebenserwartung“ (=Erwartungswert) dieser Viren?
(f) Bestimmen Sie die Varianz!