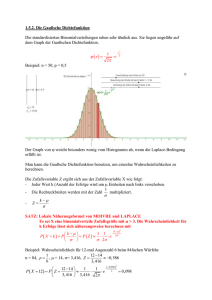
Aufgaben: Wahrscheinlichkeits

Während der Fahrt eines Autos ändert sich die Geschwindigkeit kontinuierlich. Mit einem
empfindlichen Messgerät wurden die Geschwindigkeiten eines Autos über eine Strecke in sehr
kleinen Zeitintervallen (in Meter pro Sekunde [m/s]) gemessen. Aus den Messungen wurden
dann die klassierten relativen Häufigkeiten für die Geschwindigkeiten bestimmt. Durch
Approximation der klassierten Häufigkeiten ergab sich für die Wahrscheinlichkeitsverteilung der
stetigen Zufallsvariable der Geschwindigkeiten folgende Dichtefunktion:
0 ,
f (v
)
1
1024
=
−
1
v
256
3
für
+ 4v
,
v < 0
für
0 ,
0 ≤ v ≤ 32
für
v > 32
Dichtefunktion der Geschwi ndigkeitsverteilung
f(v)
0.04
0.03
0.02
0.01
5
10
15
20
25
30
v [m/s]
Zeigen und begründen Sie, dass diese Funktion eine Dichtefunktion ist.
Berechnen Sie die durchschnittliche Geschwindigkeit des Autos.
Berechnen Sie die Standardabweichung der Geschwindigkeitsverteilung.
Berechnen Sie die Wahrscheinlichkeit dafür, dass das Auto Geschwindigkeiten zwischen v
= 15 [m/s] und v = 20 [m/s] besitzt.
Berechnen Sie die Wahrscheinlichkeit dafür, dass das Auto Geschwindigkeiten größer als
v = 12,6 [m/s] besitzt.
∞
f ist für alle v stetig und für alle v ist f (v)
f (v ) dv = 1
0 und es gilt:
− ∞
17,0667 [m/s]
7,0754 [m/s]
0,2374
0,7139
In einer Fabrik wurden die Zeiten für die Montage von Einzelteilen zur Herstellung von
Automobile-Getrieben gemessen. Die Messungen ergaben, dass die kürzeste Zeit dafür t = 1
[h] (Stunde) und die höchst Zeit dafür t = 3 [h] (Stunden) beträgt. Die
Wahrscheinlichkeitsverteilung für die Monatagezeit ergab folgende Dichtefunktion:
0 ,
f
(t )=
für
t − 1 ,
−t + 3 ,
0 ,
t < 1
1≤ t < 2
2 ≤ t ≤ 3
t > 3
für
für
für
Skizzieren Sie die den Graphen von f. Zeigen und begründen Sie, dass diese Funktion eine
Dichtefunktion ist.
Berechnen Sie die durchschnittliche Montagezeit.
Berechnen Sie die Standardabweichung der Montagezeit.
Wie groß ist die Wahrscheinlichkeit dafür, dass die Montagezeit mehr als t = 1,5 [h]
(Stunden) dauert?
Wie groß ist die Wahrscheinlichkeit dafür, dass die Montagezeit zwischen t = 1,49 [h] und
t = 1,51 [h] dauert?
∞
f ist für alle t stetig und für alle t ist f (t)
f (t ) dt = 1
0 und es gilt:
− ∞
Dichtefunktion der Zeitverteilung
f(t)
1
0.8
0.6
0.4
0.2
t [h]
-2
-1
1
2 [h]
2
3
0,408 [h]
4
5
0,875
0,01
Für die stetigen Zufallsvariable X ist die folgende Dichtefunktion gegeben.
f
(x)
=
c
x
0 ,
für
,
für
0 ,
für
x ≤ 0
0 < x < 1
x ≥ 1
Bestimmen Sie c, so dass f ( x ) die Eigenschaften einer Dichtefunktion hat. Skizzieren Sie
dann den Graphen von f . Begründen Sie, dass diese Funktion eine Dichtefunktion ist.
Berechnen Sie den Erwartungswert dieser Wahrscheinlichkeitsverteilung.
Berechnen Sie die Varianz für diese Wahrscheinlichkeitsverteilung.
Wie groß ist die Wahrscheinlichkeit für 0,2 X
0,201 ?
Wie groß ist die Wahrscheinlichkeit für X
0,2 ?
∞
f ( x ) dx = 1 folgt: c = 3/2 . Ferner ist f in
Aus der Bedingung für Dichtefunktionen
− ∞
jedem Abschnitt stetig und für alle x ist f (x)
0.
Dichtefunktion der Zufallsvariable X
f(x)
1.4
1.2
1
0.8
0.6
0.4
0.2
-2
-1
1
3/5
2
3
x
12 / 175
0,00067
0,91
Sei der Fehler der Reaktionszeit eines Temperaturmessers in °C eine stetige
Zufallsvariable mit der Dichtefunktion:
0 ,
f (θ
)
1
θ
3
=
2
θ ≤ −1
für
,
für
0 ,
für
−1< θ < 2
θ ≥ 2
Skizzieren Sie die den Graphen von f. Zeigen und begründen Sie, dass diese Funktion eine
Dichtefunktion ist.
Berechnen Sie den durchschnittlichen Fehler bei der Temperaturmessung.
Berechnen Sie die Standardabweichung des Fehlers der Temperaturmessung..
Wie groß ist die Wahrscheinlichkeit, dass der Fehler zwischen
= 0 [°C] und
= 1 [°C]
liegt?
Wie groß ist die Wahrscheinlichkeit dafür, dass der Fehler größer als
= 1,5 [°C] ist?
∞
f ist in jedem Abschnitt stetig und für alle
ist f ( )
f (θ ) dθ = 1
0 und es gilt:
− ∞
Dichtefunktion der Zufallsvariable
f(
)
1.2
1
0.8
0.6
0.4
0.2
-3
-2
-1
1
2
3
4
[°C]
5/4
0,798
1/9
37 / 72