Übung 4: Zufallsvariablen und Wahrscheinlichkeits

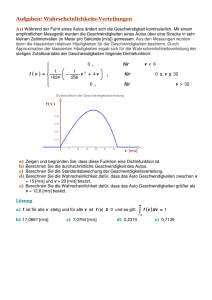
Sei die diskrete Zufallsvariable X die Anzahl defekter Bauteile in einer Stichprobe. Durch
umfangreiche Testsreihen für Bauteile einer Serienproduktion ergab sich folgende
Wahrscheinlichkeitsverteilung für die Anzahl defekter Bauteile in Stichproben vom
Umfang 3.
k
X : Anzahl defekter Bauteile in einer Stichprobe vom Umfang 3
X=xk
Wahrscheinlichkeit: Wahrscheinlichkeitsfunktion
P ( X = x k) = f (x k)
F(x)
1
2
3
4
0
1
2
3
0,1
0,01
0,51 0,38
Zeichnen Sie das Wahrscheinlichkeitsdiagramm sowie den graphischen Verlauf der
Verteilungsfunktion. Und zeigen Sie, dass f eine Wahrscheinlichkeitsfunktion ist.
Berechnen Sie die durchschnittliche Anzahl defekter Bauteile in Stichproben vom Umfang
3 aus der Serienproduktion.
Berechnen Sie die Standardabweichung für die Anzahl defekter Bauteile in Stichproben
vom Umfang 3 aus der Serienproduktion.
Wie groß ist die Wahrscheinlichkeit dafür, dass sich höchstens 1 defekter Bauteil in der
Stichprobe befindet?
Wie groß ist die Wahrscheinlichkeit dafür, dass sich mindestens 2 defekte Bauteile in der
Stichprobe befinden?
Lösung:
b) µ = 0,6
c) σ ² = 0,4979 ; σ = 0,705
d) P(X 1) = 0,89
e) P(X > 1) = 0,11
In einer Fabrik wurden die Zeiten für die Montage von Einzelteilen zur Herstellung von
Automobil-Getrieben gemessen. Die Messungen ergaben, dass die kürzeste Zeit dafür t
= 1 [h] (Stunde) und die höchst Zeit dafür t = 3 [h] (Stunden) beträgt. Die
Wahrscheinlichkeitsverteilung für die Monatagezeit ergab folgende Dichtefunktion:
0 ,
f
(t )=
t − 1 ,
−t + 3 ,
0 ,
für
für
für
für
t < 1
1≤ t < 2
2 ≤ t ≤ 3
t > 3
Skizzieren Sie die den Graphen von f. Zeigen und begründen Sie, dass diese Funktion
eine Dichtefunktion ist.
Berechnen Sie die durchschnittliche Montagezeit.
Berechnen Sie die Standardabweichung der Montagezeit.
Wie groß ist die Wahrscheinlichkeit dafür, dass die Montagezeit mehr als t = 1,5 [h]
(Stunden) dauert?
Wie groß ist die Wahrscheinlichkeit dafür, dass die Montagezeit zwischen t = 1,49 [h]
und t = 1,51 [h] dauert?
Lösung: a)
Dichtefunktion der Zeitverteilung
f(t)
1
0.8
0.6
0.4
0.2
t [h]
-2
b) 2 [h]
-1
1
c) 0,408 [h]
2
3
d) 0,875
4
5
e) 0,01