Ubungsblatt 1 - wiwi.uni

Fortgeschrittene Statistik
Prof. Dr. Bernd Wilfling
Dipl.-Phys. Robert Hahn
Wintersemester 2012/2013
Übungsblatt 1
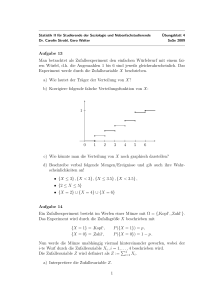
1. (a) Was sind die Charakteristika einer Verteilungsfunktion?
(b) Es seien F1 (x) und F2 (x) Verteilungsfunktionen. Überprüfen Sie, ob die
folgenden Funktionen Verteilungsfunktionen sind:
F3 (x) = λF1 (x) + (1 − λ)F2 (x), 0 ≤ λ ≤ 1.
(
F1 (x) für x < 0
.
F4 (x) =
F2 (x) für x ≥ 0
F5 (x) = F1 (x) · F2 (x).
F6 (x) = max{F1 (x), F2 (x)}.
F7 (x) = F1 (x)(1 − exp (−x)).
F8 (x) = F1 (x)2 .
2. In Matheklausuren machen Studierende typischerweise 3 Arten von Flüchtigkeitsfehlern: Vorzeichenfehler(F1 ), falsches Setzen von Klammern (F2 ) und Eingabefehler bei der Benutzung des Taschenrechners (F3 ). Empirische Untersuchungen
haben die folgenden Wahrscheinlichkeiten ergeben:
P (F1 ) = 0, 08.
P (F2 ) = 0, 06.
P (F3 ) = 0, 2.
P (F1 ∩ F2 ) = 0, 01.
P (F1 ∩ F3 ) = 0, 06.
P (F2 ∩ F3 ) = 0, 03.
P (F1 ∩ F2 ∩ F3 ) = 0, 005 .
1
Wie hoch sind die Wahrscheinlichkeiten für das Auftreten der folgenden Ereignisse?
(a) Keiner der oben genannten Flüchtigkeitsfehler tritt auf.
(b) Es liegt kein Vorzeichen- oder Klammerfehler vor.
(c) Es wurde korrekt in den Taschenrechner eingetippt und richtig geklammert.
3. Gegeben seien folgende Mengen:
A = {1, 2, 3}.
B = {1, 3, 5}.
C = {2, 4, 6}.
D = {2, 5} .
Bestimmen Sie die folgenden Mengen bzw. drücken Sie die Mengen durch A,B,C
und D aus.
(a) A ∩ B̄.
(b) C ∪ D.
(c) A ∪ (B ∩ C).
(d) (A ∪ B) ∩ C.
(e) A \ B.
(f) {2}.
(g) {1, 2, 3, 4, 6}.
(h) {1, 3, 4, 6}.
4. Beweisen oder widerlegen Sie folgende Aussagen:
(a) Wenn P (A) = P (B̄), dann gilt Ā = B.
(b) Wenn P (A) = P (B) = p, dann gilt P (A ∩ B) ≤ p2 .
(c) Wenn P (A) = 0, dann gilt P (A ∩ B) = 0.
(d) Wenn P (A) = 0, dann gilt A = ∅.
(e) Wenn P (Ā) = α und P (B̄) = β, dann gilt P (A ∩ B) ≥ 1 − α − β.
2
5. Zeigen Sie, dass die folgenden Funktionen Wahrscheinlichkeitsdichten sind oder
geben Sie ein Gegenbeispiel an:
(a) f1 (x) = exp(−x), x ∈ (0, ∞).
(b) f2 (x) = 2 exp(−2x), x ∈ (0, ∞).
(c) f3 (x) =
1
,x
x2
∈ (1, ∞).
(d) f4 (x) = (θ + 1)f1 (x) − θf2 (x), θ ∈ (0, 1).
6. Bestimmen Sie den Erwartungswert von
(a) X, wenn X die Dichte f3 (x) hat.
(b) sin(X), wenn X die Dichte fX (x) =

1
, −1
2
≤x<1
aufweist.
0 sonst
(c) X, wenn X Laplaceverteilt auf den Werten 5 bis 9 ist.
(d) X, wenn X exponentialverteilt ist.

,0 < x ≤ 1
 0.5x
0.5
, 1 < x ≤ 2 aufweist.
(e) X, wenn X die Dichte fX (x) =

1.5 − 0.5x , 2 < x ≤ 3
7. Es seien X eine beliebige Zufallsvariable (diskret oder stetig), c, c1 , c2 ∈ R konstante Zahlen und g, g1 , g2 : R → R Funktionen. Beweisen Sie die folgenden
Aussagen:
(a) E(c) = c.
(b) E[c · g(X)] = c · E[g(X)].
(c) E[c1 · g1 (X) + c2 · g2 (X)] = c1 · E[g1 (X)] + c2 · E[g2 (X)].
(d) Falls g1 (x) ≤ g2 (x) für alle x ∈ R gilt, so folgt:
E[g1 (x)] ≤ E[g2 (x)].
8. X sei eine beliebige Zufallsvariable (diskret oder stetig) und a, b ∈ R (beliebig
aber fest). Beweisen Sie die folgenden Aussagen:
(a) V (a) = 0.
(b) V (X) = E(X 2 ) − [E(X)]2 .
(c) V (a + b · X) = b2 · V (X),
3
9. Berechnen Sie die Varianz
(a) der Zufallsvariable X mit der zugehörigen Dichtefunktion

0.5x
,0 < x ≤ 1

fX (x) = 0.5
,1 < x ≤ 2 .


1.5 − 0.5x , 2 < x ≤ 3
(b) der Zufallsvariable X mit der Dichtefunktion f3 (x) aus Aufgabe 1.
4