5. ¨Ubungswoche

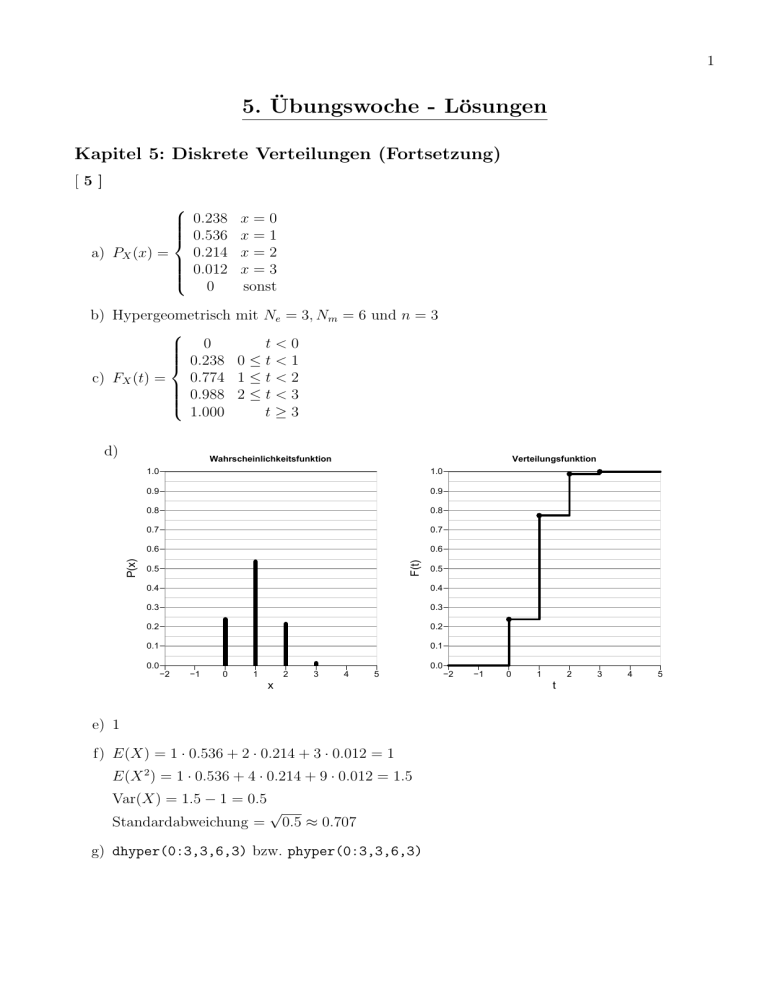
1
5. Übungswoche - Lösungen
Kapitel 5: Diskrete Verteilungen (Fortsetzung)
[5]

0.238 x = 0




 0.536 x = 1
0.214 x = 2
a) PX (x) =


0.012 x = 3



0
sonst
b) Hypergeometrisch

0




 0.238
0.774
c) FX (t) =


0.988



1.000
d)
mit Ne = 3, Nm = 6 und n = 3
t<0
0≤t<1
1≤t<2
2≤t<3
t≥3
Verteilungsfunktion
1.0
0.9
0.9
0.8
0.8
0.7
0.7
0.6
0.6
F(t)
P(x)
Wahrscheinlichkeitsfunktion
1.0
0.5
0.5
0.4
0.4
0.3
0.3
0.2
0.2
0.1
0.1
0.0
0.0
−2
−1
0
1
2
3
4
5
x
f) E(X) = 1 · 0.536 + 2 · 0.214 + 3 · 0.012 = 1
E(X 2 ) = 1 · 0.536 + 4 · 0.214 + 9 · 0.012 = 1.5
Standardabweichung =
√
−1
0
1
2
t
e) 1
Var(X) = 1.5 − 1 = 0.5
−2
0.5 ≈ 0.707
g) dhyper(0:3,3,6,3) bzw. phyper(0:3,3,6,3)
3
4
5
2
[6]
a) Wahrscheinlichkeitsfunktion der hypergeometrischen Verteilung mit den Parametern Ne =
250, Nm = 750 und n = 8 für x = 0, 1 und 2
b) Biomialverteilung mit n = 8 und π = 250/1 000 = 1/4 = 0.25
c) 0.1001; 0.2670; 0.3115
d) round(dbinom(0:2,8,1/4),4)
e) n sollte kleiner als 5% des Minimums von Ne und Nm sein, d.h. kleiner als 5% von 250, d.h.
n sollte kleiner als 12.5 sein. Hier ist n = 8, d.h. die Bedingung ist erfüllt.
f) Hypergeometrisch: FX (t) = 0.0992; 0.3662; 0.6789
Binomial:
FX (t) = 0.1001; 0.3671; 0.6786
g) phyper(0:2,250,750,8) bzw. pbinom(0:2,8,0.25)
[ 7 ] Ziehen mit und ohne Zurücklegen
Eine Grundgesamtheit bestehe aus Ne Erfolgen und Nm Misserfolgen. Es werde n-mal aus dieser
Grundgesamtheit gezogen.
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
a) Wird mit Zurücklegen gezogen, so ist die Anzahl der Erfolge exakt binomialverteilt mit (
den Parametern n und π = Nm /(Ne + Nm ).
)
b) Es werde mit Zurücklegen gezogen, es sei Ne = Nm und n sehr groß. Dann ist die ( × )
Anzahl der Erfolge annähernd N (n/2, n/4)-verteilt.
c) Wird ohne Zurücklegen gezogen, so ist die Anzahl der Erfolge exakt hypergeometrisch ( × )
verteilt.
d) Unabhängig von den Werten der Parameter Ne und Nm ist die hypergeometrische (
Verteilung immer gut durch eine Binomialverteilung zu approximieren, wenn nur n
groß genug ist.
)
e) Sind die Voraussetzungen für eine Approximation der hypergeometrischen Verteilung ( × )
durch die Binomialverteilung erfüllt, so gilt π = Ne /(Ne + Nm ).
3
[ 8 ] Poissonverteilung
Die folgenden Aussagen beziehen sich auf eine poissonverteilte Zufallsvariable mit dem Parameter
λ.
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
a) Ist X ∼ Po(10)-verteilt, so kann X nur die Werte 0, 1, 2, . . . , 10 annehmen.
b) Für eine poissonverteilte Zufallsvariable gilt E(X) = Var(X).
(
)
(×)
c) Mit wachsendem Wert des Parameters λ wird die Wahrscheinlichkeitsfunktion der Pois- ( × )
sonverteilung breiter und flacher.
d) Die möglichen Werte einer poissonverteilten Zufallsvariable X sind 1, 2, 3 . . ..
(
e) P (0) = P (X = 0) = e
(×)
−λ
> 0 für alle λ > 0.
)
f) Für großes λ ähnelt die Wahrscheinlichkeitsfunktion der Dichtefunktion einer Normal- ( × )
verteilung.
g) Es gilt E(X) = λ und Var(X) = λ2 .
(
)
h) Die Poissonverteilung hat einen Parameter λ, wobei λ = 1/E(X) gilt.
(
)
i) Die Poissonverteilung ist symmetrisch um den Parameter λ.
(
)
j) Die Poissonverteilung kann für große λ durch eine Binomialverteilung approximiert (
werden.
)
[ 9 ] Punkte: 2 SS09K1
Die Anzahl X der Reparaturfälle an einem Fließband in einem Jahr sei poissonverteilt mit dem
Erwartungswert E(X) = 2.6.
• Berechnen Sie die Wahrscheinlichkeit, dass es mindestens einen Reparaturfall in einem
Jahr gibt oder
• geben Sie einen R-Befehl für die Berechnung dieser Wahrscheinlichkeit an.
Wahrscheinlichkeit:
0.926
oder
1 - ppois(0,2.6)
oder
1 - dpois(0, 2.6)
4
[ 10] SS09K2
Die folgenden Aussagen befassen sich mit der hypergeometrischen Verteilung.
a) Der Parameter n darf nicht größer als Ne + Nm sein.
b) Für eine hypergeometrisch verteilte Zufallsvariable gilt stets X ≤ Ne .
c) Die hypergeometrische Verteilung h(Ne , Nm , n) kann unter gewissen Voraussetzungen
durch eine Binomialverteilung mit den Parametern n und Ne /(Ne + Nm ) approximiert
werden.
d) Die hypergeometrische Verteilung hat zwei Parameter.
e) Eine hypergeometrische Zufallsvariable kann als Anzahl der Erfolge bei n Ziehungen mit
Zurücklegen aus einer Grundgesamtheit mit Ne Erfolgen und Nm Misserfolgen aufgefasst
werden.
Kreuzen Sie jetzt genau eine der folgenden fünf Möglichkeiten an:
WAHR sind die folgenden Aussagen:
a,b,c
(
)
a,b,d
(
b,c,d
)
(
)
b,c,e
(
c,d,e
)
(
)
Wahr sind: a,b,c
Kapitel 6: Stetige Verteilungen
[ 1 ] a) E(X) = 25; Var(X) = 625
(
0
t<0
c) FX (t) =
−0.04t
1−e
t≥0
b) i) 0.632; 0.865; 0.950
ii) 0.091; 0.027; 0.008
d) 1−FX (t) = e−0.04t für t ≥ 0.
pexp(c(25,50,75),0.04)
1-pexp(c(60,90,120),0.04)
pexp(50,0.04)-pexp(25,0.04)
1-pexp(c(30,60,100,200,365),0.04)
iii) 0.233
0.301; 0.091; 0.018; 0.000; 0.000
5
[2]
i) P (X ≤ 197) = Φ( 197−183
) = 0.841;
14
P (X ≤ 200) = Φ( 200−183
) = 0.887;
14
211−183
P (X ≤ 211) = Φ( 14 ) = 0.977
a)
Dichtefunktion
0.04
0.03
0.03
y = f(x)
y = f(x)
Dichtefunktion
0.04
0.02
0.01
0.841
0.02
0.841
0.01
0.00
140 150 160 170 180 190 200 210 220 230
0.00
140 150 160 170 180 190 200 210 220 230
Blockzeit (Minuten)
Blockzeit (Minuten)
pnorm(197,183,14)
) = 0.841;
ii) P (X > 169) = 1 − Φ( 169−183
14
P (X > 175) = 1 − Φ( 175−183
) = 0.716;
14
155−183
P (X > 155) = 1 − Φ( 14 ) = 0.977
1-pnorm(169,183,14)
) − Φ( 169−183
) = 0.682;
iii) P (169 < X ≤ 197) = Φ( 197−183
14
14
211−183
155−183
P (155 < X ≤ 211) = Φ( 14 ) − Φ( 14 ) = 0.954;
P (170 ≤ X ≤ 200) = Φ( 200−183
) − Φ( 170−183
) = 0.711
14
14
Dichtefunktion
0.04
y = f(x)
0.03
0.02
0.01
0.683
0.00
140 150 160 170 180 190 200 210 220 230
Blockzeit (Minuten)
pnorm(197,183,14)-pnorm(169,183,14)
6
b) P (X ≤ k) = 0.95
Φ( k−183
) = 0.95
14
⇔
⇔
k−183
14
= 1.64
0.04
0.03
0.03
0.02
0.01
k = 205.96
Dichtefunktion
0.04
y = f(x)
y = f(x)
Dichtefunktion
⇔
0.95
0.02
0.90
0.01
0.00
140 150 160 170 180 190 200 210 220 230
0.00
140 150 160 170 180 190 200 210 220 230
Blockzeit (Minuten)
Blockzeit (Minuten)
qnorm(0.95,183,14)
c) P (X > k) = 0.90
⇔
−1.28 ⇔ k = 165.08
P (X ≤ k) = 0.1
⇔
) = 0.1
Φ( k−183
14
⇔
k−183
14
=
qnorm(0.1,183,14) oder qnorm(0.9,183,14,lower.tail=FALSE)
k1 −183
d) P (X < k1 ) = 0.05 ⇔ Φ( k1 −183
) = 0.05 ⇔
= −1.64
14
14
k2 −183
k2 −183
= 1.64
und P (X > k2 ) = 0.05 ⇔ Φ( 14 ) = 0.95 ⇔
14
P (k1 ≤ X ≤ k2 ) = 0.9
⇔
⇔
k1 = 160.04
k2 = 205.96
Dichtefunktion
0.04
y = f(x)
0.03
0.02
0.01
0.90
0.00
140 150 160 170 180 190 200 210 220 230
Blockzeit (Minuten)
qnorm(0.05,183,14) und qnorm(0.95,183,14) oder qnorm(0.05,183,14,lower.tail=FALSE)
7
[ 3 ] Rechteckverteilung
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
a) Der Erwartungswert einer Rechteckverteilung im Intervall [a, b] ist genau die Mitte des ( × )
Intervalls [a, b].
b) Auch die Varianz einer Rechteckverteilung im Intervall [a, b] liegt im Intervall [a, b].
(
)
c) Es gibt nur drei stetige Verteilungen: die Rechteckverteilung, die Exponentialverteilung (
und die Normalverteilung.
)
d) Die Rechteckverteilung hat zwei Parameter a und b und das Intervall [a, b] ist der ( × )
Bereich der möglichen Werte.
e) Die Verteilungsfunktion einer rechteckverteilten Zufallsvariablen mit den Parametern ( × )
a und b ist im Intervall [a, b] eine Gerade mit der Steigung 1/(b − a).
f) Die Dichtefunktion der Rechteckverteilung mit Werten im Intervall [a, b] ist über diesem (
Intervall eine waagerechte Gerade y = b−a, d.h. die Dichtefunktion bildet ein Rechteck
über [a, b] mit der Höhe b − a.
)
g) Für die Rechteckverteilung im Intervall (a,b) gilt: Je größer die Länge des Intervalls, (
desto kleiner ist die Varianz.
)
h) Die Rechteckverteilung verdankt ihren Namen dem Graphen ihrer Verteilungsfunktion. (
)
i) Der Graph der Rechteckverteilungsfunktion ist linear.
(×)
j) Die Wahrscheinlichkeit, dass eine U (a, b)-verteilte ZV in [a1 , b1 ] ⊂ [a, b] fällt, hängt nur ( × )
von der Länge, nicht von der Lage des Intervalls [a1 , b1 ] ab.
k) Man spricht von einer Rechteckverteilung, wenn zwei Zufallsvariablen X und Y nur (
Werte in einem Rechteck annehmen können.
)
[ 4 ] Normalverteilung
Welche der folgenden Aussagen sind WAHR? Kreuzen Sie sie an.
a) Für die Standardnormalverteilung gilt P (−µ < X < µ) ≈ 0.68.
(
c) Für die Standardnormalverteilung gilt P (X ≤ −1) = P (X ≥ 1).
(×)
b) Die Dichtefunktion der Normalverteilung ist symmetrisch um x = µ.
d) Für die Normalverteilung gilt P (X ≤ µ) = 0.5
)
(×)
(×)
e) Für die Normalverteilung gilt, je größer σ 2 , desto schmaler und höher wird die Dichte- (
funktion.
)
f) Für die Normalverteilung gilt: Der Parameter µ bestimmt nur die Lage, nicht die ( × )
Gestalt der Dichtefunktion.
g) Die Verteilungsfunktion einer N (µ; σ 2 )-verteilten Zufallsvariablen hängt nicht von den (
Parametern ab.
)
h) Die Normalverteilung wird wegen ihrer komplizierten Dichtefunktion eher selten ver- (
wendet.
)
i) Falls Z ∼ N (0, 1) und X ∼ N (µ, σ 2 ), so gilt für alle möglichen werte von µ und σ 2 : ( × )
P (−1 ≤ Z ≤ 1) = P (µ − σ < X < µ + σ) ≈ 0.68.
j) Die Dichtefunktion einer Normalverteilung ist immer symmetrisch um x = 0.
(
)