Konfidenzintervalle Die Bestimmung von Quantilen mit Hilfe von R

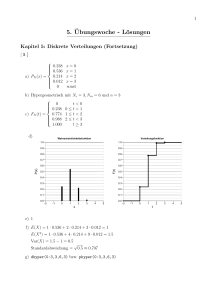
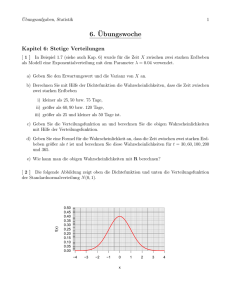
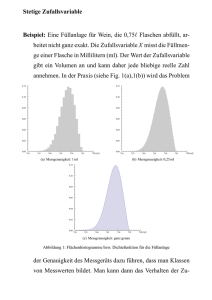
Statistik – R
7. Übung
WS 2010/11
Konfidenzintervalle
Die Bestimmung von Quantilen mit Hilfe von R kann aus der folgenden Tabelle entnommen
werden.
Verteilung
„Name der Verteilung“
Quantile
Rechteckverteilung
unif
qunif(p,min,max)
Exponentialverteilung
exp
qexp(p,rate)
Normalverteilung
norm
qnorm(p,mean,sd)
Student-t-Verteilung
t
qt(p,df)
Chiquadrat-Verteilung
chisq
qchisq(p,df)
F-Verteilung
f
qf(p,df1,df2)
Hinweis:
In R wird bei Eingabe der obigen Befehle immer das untere Quantil ausgegeben.
qnorm(0.05,0,1)
[1] -1.644854
qnorm(0.95,0,1)
[1] 1.644854
Schauen Sie sich zur Veranschaulichung eine Standnormalverteilung an, probieren Sie folgende
Befehle aus und diskutieren Sie was sie bewirken:
•
qnorm(0.1,0,1)
•
qnorm(0.1,0,1,lower.tail=F)
•
qnorm(0.9)
•
qnorm(0.9,lower.tail=F)
Statistik – R
7. Übung
WS 2010/11
Aufgabe 1:
Betrachten Sie für diese Übung den Datensatz gluehbirne.dat, den Sie schon aus der
Vorlesung kennen. Laden Sie ihn dazu mit Hilfe des Befehls source(“Link“) aus dem Internet.
(1) Stellen Sie die in gluehbirne.dat gespeicherten Daten zunächst in einem normierten
Histogramm dar.
(2) Nehmen Sie an, die Beobachtungen seien normalverteilt. Schätzen Sie die entsprechenden
Parameter und damit die Dichtefunktion.
(3) Um die Dichtefunktion über das Histogramm zeichnen zu können, müssen Sie zunächst den
Definitionsbereich Ihrer Dichtefunktion bestimmen. Betrachten Sie hierzu das Histogramm und
speichern dann die entsprechende Sequenz unter x ab. Zeichnen Sie nun die Dichtefunktion
über das Histogramm.
(4) Erzeugen Sie nun mit Hilfe von
rnorm(30,mean(gluehbirne.dat),sd(gluehbirne.dat)) eine Stichprobe der
Größe n = 30 und speichern Sie diese unter gluehsp1.dat.
(5) Teilen Sie das Grafikfenster mit Hilfe des Befehls par(mfrow=c(2,1)) in zwei Bereiche
auf.
(6) Zeichnen Sie anschließend in den oberen Bereich die Dichtefunktion mit den von Ihnen
geschätzten Parametern. (Lassen Sie das Grafikfenster für die nächsten Teilaufgaben geöffnet.)
(7) Mit Hilfe der selbstgeschriebenen Funktion konfi.fun(daten,Konfidenzniveau)
können Sie das Konfidenzintervall [C-;C+] für µ bei unbekanntem σ² bestimmen. Bestimmen
Sie die Grenzen der Konfidenzintervalle für den Mittelwert der erzeugten Stichprobe mit
folgenden Konfidenzniveaus: 0.99, 0.95, 0.90.
(8) Erzeugen Sie nun eine Stichprobe der Größe n = 300 und speichern Sie die Werte ab.
Wiederholen Sie die Schritte 6) und 7). Was fällt Ihnen auf?
Aufgabe 2:
Berechnen Sie die Aufgabe 11 aus den Übungsaufgaben zu Kapitel 8 aus dem WS 2007/08, die Sie
im Internet finden, ( Lehre Veranstaltungen im WS 2007/08 Statistik Übungsaufgaben
der Kleinübungen) mit Hilfe von R.. Beachten Sie, dass zum Berechnen dieses Konfidenzintervalls
Werte aus einer Chiquadrat- Verteilung benötigt werden.