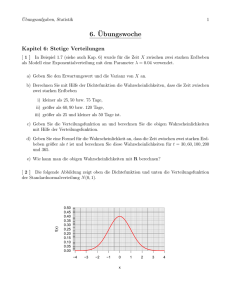
Stetige Verteilungen und Approximationen Innerhalb der Statistik

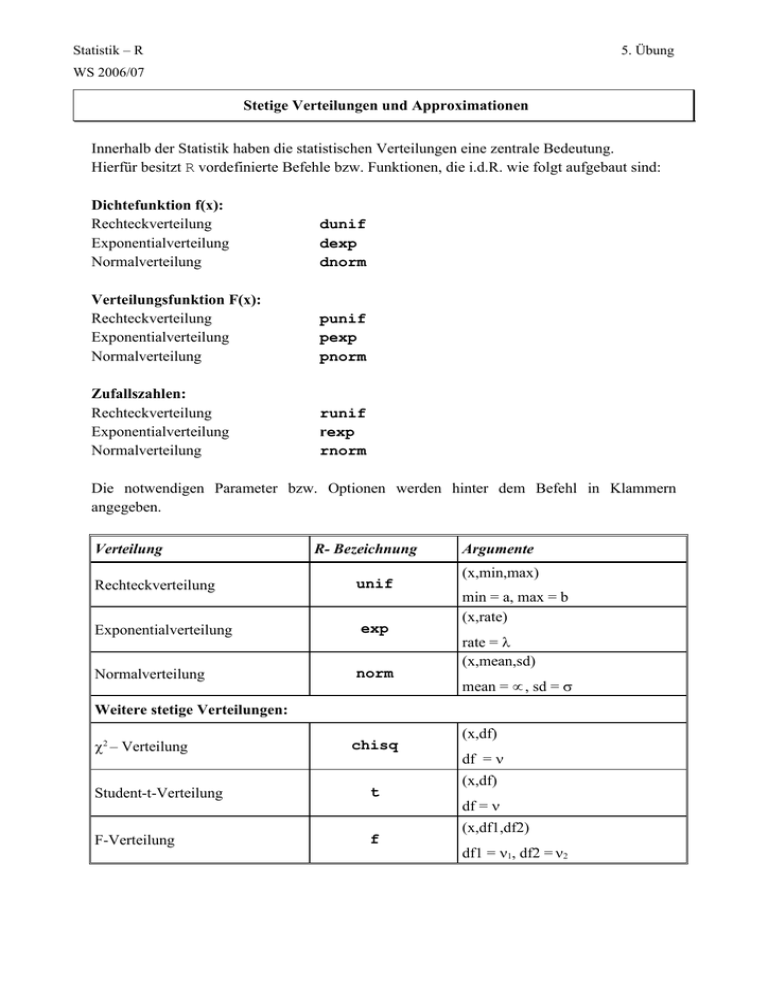
Statistik – R
5. Übung
WS 2006/07
Stetige Verteilungen und Approximationen
Innerhalb der Statistik haben die statistischen Verteilungen eine zentrale Bedeutung.
Hierfür besitzt R vordefinierte Befehle bzw. Funktionen, die i.d.R. wie folgt aufgebaut sind:
Dichtefunktion f(x):
Rechteckverteilung
Exponentialverteilung
Normalverteilung
dunif
dexp
dnorm
Verteilungsfunktion F(x):
Rechteckverteilung
Exponentialverteilung
Normalverteilung
punif
pexp
pnorm
Zufallszahlen:
Rechteckverteilung
Exponentialverteilung
Normalverteilung
runif
rexp
rnorm
Die notwendigen Parameter bzw. Optionen werden hinter dem Befehl in Klammern
angegeben.
Verteilung
Rechteckverteilung
Exponentialverteilung
Normalverteilung
R- Bezeichnung
unif
exp
norm
Argumente
(x,min,max)
min = a, max = b
(x,rate)
rate = λ
(x,mean,sd)
mean = µ , sd = σ
Weitere stetige Verteilungen:
χ2 – Verteilung
chisq
Student-t-Verteilung
t
F-Verteilung
f
(x,df)
df = ν
(x,df)
df = ν
(x,df1,df2)
df1 = ν1, df2 = ν2
Statistik – R
5. Übung
WS 2006/07
Aufgabe 1:
Die Datei „Datensätze 5.Übung.txt“ enthält die beiden Datensätze daten1.dat und daten2.dat. Diese
sollen im Rahmen der folgenden beiden Aufgaben bearbeitet werden:
•Laden
Sie dazu zunächst die Datensätze in R. Benutzen Sie den Befehl source(“ Link “)
•Stellen Sie nun den Datensatz daten1.dat in einem Histogramm (mit prob=T) graphisch dar.
Überlegen Sie welche Verteilung diesem Datensatz zugrunde liegen könnte!
•Speichern
Sie
eine
Sequenz
von
0
bis
15
der
Länge
100
unter
x
ab
( x<-seq(0,15,length=100)). Zeichnen Sie nun Dichten der Exponentialverteilung mit
verschiedenen Werten für λ (0.33, 0.5, 3) ein. Benutzen Sie hierfür den R-Befehl
lines(x,dexp(x,rate)). Welche Dichtefunktion beschreibt das Modell Ihrer Meinung nach
am besten?
•Berechnen
Sie mit dem λ, der von Ihnen gewählten Dichtefunktion, die folgenden
Wahrscheinlichkeiten:
(a)P(X < 0.5)
(b)P(0.2< X < 0.7)
(c)P(X>1)
Aufgabe 2:
Verfahren Sie analog zu Aufgabe 1:
•Stellen Sie daten2.dat in einem Histogramm (mit prob=T) graphisch dar. Welcher Verteilung
ähnelt dieses Histogramm?
•Benutzen Sie den Befehl: x<-seq(-2,12,length=100) um eine Sequenz von –2 bis 12 der
Länge 100 unter x abzuspeichern. Legen Sie mit Hilfe des Befehls
lines(x,dnorm(x,mean,sd)) verschiedene Dichten der
Normalverteilung über das
Histogramm. Probieren Sie dabei die folgenden Parameterkombinationen aus:
(μ = 3 und σ = 2; μ = 5 und σ = 3; μ = 5 und σ =2).
Aufgabe 3:
Betrachten Sie ein Zufallsexperiment, bei dem eine faire Münze 100-mal geworfen wird. Die
Zufallsvariable X sei definiert als die Anzahl der dabei aufgetretenen Seite „Kopf“.
•Stellen Sie die Wahrscheinlichkeitsfunktion dieser Binomialverteilung mit dem Befehl
plot(0:100,dbinom(0:100,size,prob),type=“h“)
graphisch dar. Geben Sie dabei für size und prob die entsprechenden Parameter an.
Statistik – R
5. Übung
WS 2006/07
•Berechnen Sie die folgenden Wahrscheinlichkeiten mit Hilfe des Befehls
pbinom(q,size,prob):
1.Die Wahrscheinlichkeit höchstens 50 mal Kopf zu erhalten.
2.Die Wahrscheinlichkeit mindestens 50 mal und höchstens 55 mal Kopf zu erhalten.
•Zeichnen
Sie
die
Dichtefunktion
der
approximierenden
Normalverteilung
über
die
Wahrscheinlichkeitsfunktion der Binomialverteilung. Definieren Sie hierzu mit dem Befehl
x<-seq(0,100,length=1000)
einen Vektor der x-Werte und mit
y<-dnorm(x,mean,sd)
die zugehörigen Werte der Dichtefunktion. Benutzen Sie lines(x,y,type=“l“) um die
Dichtefunktion einzuzeichnen. Vergleichen Sie beide Verteilungen.
•Berechnen Sie die Wahrscheinlichkeiten aus (2) mit Hilfe der approximierenden Normalverteilung
(pnorm(q,mean,sd)) mit und ohne Stetigkeitskorrektur.
Vergleichen Sie die Werte.