Was wird berechnet? Innerhalb der Statistik haben die statistischen
Werbung
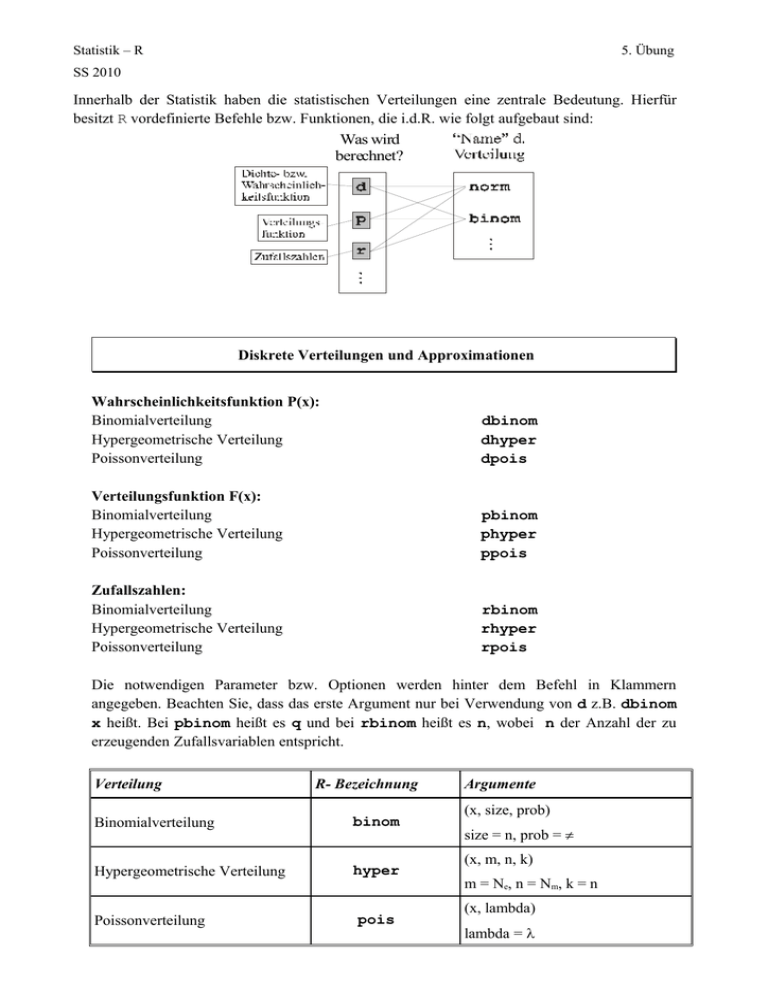
Statistik – R 5. Übung SS 2010 Innerhalb der Statistik haben die statistischen Verteilungen eine zentrale Bedeutung. Hierfür besitzt R vordefinierte Befehle bzw. Funktionen, die i.d.R. wie folgt aufgebaut sind: Was wird berechnet? Diskrete Verteilungen und Approximationen Wahrscheinlichkeitsfunktion P(x): Binomialverteilung Hypergeometrische Verteilung Poissonverteilung dbinom dhyper dpois Verteilungsfunktion F(x): Binomialverteilung Hypergeometrische Verteilung Poissonverteilung pbinom phyper ppois Zufallszahlen: Binomialverteilung Hypergeometrische Verteilung Poissonverteilung rbinom rhyper rpois Die notwendigen Parameter bzw. Optionen werden hinter dem Befehl in Klammern angegeben. Beachten Sie, dass das erste Argument nur bei Verwendung von d z.B. dbinom x heißt. Bei pbinom heißt es q und bei rbinom heißt es n, wobei n der Anzahl der zu erzeugenden Zufallsvariablen entspricht. Verteilung R- Bezeichnung Binomialverteilung binom Hypergeometrische Verteilung hyper Poissonverteilung pois Argumente (x, size, prob) size = n, prob = π (x, m, n, k) m = Ne, n = Nm, k = n (x, lambda) lambda = λ Statistik – R 5. Übung SS 2010 Stetige Verteilungen und Approximationen Dichtefunktion f(x): Rechteckverteilung Exponentialverteilung Normalverteilung dunif dexp dnorm Verteilungsfunktion F(x): Rechteckverteilung Exponentialverteilung Normalverteilung punif pexp pnorm Zufallszahlen: Rechteckverteilung Exponentialverteilung Normalverteilung runif rexp rnorm Die notwendigen Parameter bzw. Optionen werden hinter dem Befehl in Klammern angegeben (Beachten Sie die Bemerkung bei den diskreten Verteilungen). Verteilung R- Bezeichnung Rechteckverteilung unif Exponentialverteilung exp Normalverteilung norm Argumente (x,min,max) min = a, max = b (x,rate) rate = λ (x,mean,sd) mean = µ , sd = σ Weitere stetige Verteilungen: χ2 – Verteilung chisq Student-t-Verteilung t F-Verteilung f (x,df) df = ν (x,df) df = ν (x,df1,df2) df1 = ν1, df2 = ν2 Statistik – R 5. Übung SS 2010 Aufgabe 1: Gegeben sei eine Poissonverteilung mit λ = 5. •Berechnen Sie die Wahrscheinlichkeitsfunktion P(x) für 0 ≤ x ≤ 15. Runden Sie auf 3 Nachkommastellen. (Syntax: round(x,digits), rundet die einzelnen Elemente des Vektors x auf die Anzahl der Nachkommastellen digits) •Stellen Sie P(x) graphisch dar. •Berechnen Sie nun die Wahrscheinlichkeit P(X > 2) mit Hilfe der Verteilungs- funktion. •Ermitteln Sie außerdem die Wahrscheinlichkeit P(2 < X ≤ 5) und P(3 ≤ X ≤ 5). Aufgabe 2: In Aufgabe 2 der vierten Übungswoche hatten wir 20 Kugeln aus 1500 Kugeln (davon sind 1000 Kugeln weiß und 500 Kugeln schwarz) mit Zurücklegen gezogen. Zum Berechnen der Wahrscheinlichkeitsfunktion hatten wir die Binomialverteilung verwendet. •Berechnen Sie nun die Wahrscheinlichkeitsfunktion P(x) für die Anzahl der Erfolge (Anzahl der weißen Kugeln) beim Fall der Ziehung ohne Zurücklegen. •Vergleichen Sie graphisch die Hypergeometrische Verteilung und deren Approximation durch die Binomialverteilung. Benutzen Sie dazu den Befehl: Approx.fun(x,Ne,Nm,n). Dieser erzeugt ein Säulendiagramm der Wahrscheinlichkeitsfunktionen einer hypergeometrischen Verteilung und einer Binomialverteilung mit den entsprechenden Parametern. Handelt es sich um eine sinnvolle Approximation? Wie sieht es mit der Approximation bei folgenden Werten aus: Ne=20, Nm=30,n=10? •Stellen Sie jetzt die Wahrscheinlichkeitsfunktion der am Anfang beschriebenen Bi- nomialverteilung grafisch dar. Zeichnen Sie die Dichtefunktion der approximierenden Normalverteilung über die Wahrscheinlichkeitsfunktion dieser Binomialverteilung. Definieren Sie hierzu mit dem Befehl x1<-seq(0,20,length=1000) einen Vektor der x-Werte und mit y1<-dnorm(x1,mean,sd) die zugehörigen Werte der Dichtefunktion. Benutzen Sie lines(x1,y1) um die Dichtefunktion einzuzeichnen. Vergleichen Sie beide Verteilungen.











