Folien 47 - Fakultät Informatik/Mathematik

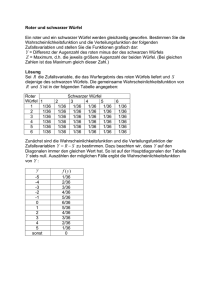
Weitere Aussagen zu normalverteilten Zufallsvariablen
Sei X eine N (µ; σ 2 )-normalverteilte Zufallsvariable.
Es wird die folgende Problemstellung betrachtet:
Mit welcher Wahrscheinlichkeit ist der Abstand beliebiger Werte
vom Erwartungswert µ kleiner als ein vorgegebenes ε > 0 ?
Lösung:
Es ist die Wahrscheinlichkeit P (|X − µ| < ε) zu berechnen.
Dazu wird ε = uσ gesetzt und der Zusammenhang mit der StandardNormalverteilung genutzt:
|X − µ|
P (|X − µ| < uσ) = P
< u = P (|U | < u) = P (−u < U < u)
σ
= P (U < u) − P (U < −u) = Φ(u) − Φ(−u) = Φ(u) − (1 − Φ(u))
= 2Φ(u) − 1 .
Daraus erhält man:
für u = 1 :
P (|X − µ|) < σ) = 2Φ(1) − 1 = 0.6827
für u = 2 :
P (|X − µ|) < 2σ) = 2Φ(2) − 1 = 0.9545
für u = 3 :
P (|X − µ|) < 3σ) = 2Φ(3) − 1 = 0.9973 .
Schlussfolgerung: Bei einer N (µ; σ 2 )-normalverteilten Zufallsvariablen liegen
99.73 % aller Werte (d.h. fast alle Werte) innerhalb der 3σ-Grenzen.
Mathematik III - Folie 47
Mathematische Statistik - Einführung, einige Grundbegriffe
Grundlegende Aufgabe der Statistik:
Gewinnung von Kenntnissen und Informationen über die Eigenschaften oder Merkmale einer bestimmten Menge von Objekten (Elementen), ohne dass dabei alle
Objekte in die Untersuchung einbezogen werden müssen
Grundgesamtheit: Gesamtheit gleichartiger Objekte oder Elemente, die hinsichtlich eines bestimmten Merkmals zu untersuchen sind; Merkmal wird durch
Zufallsvariable X beschrieben
Zufallsstichprobe vom Umfang n: eine aus der Grundgesamtheit zufällig herausgegriffene Teilmenge mit n Elementen (dabei: Auswahl der Elemente wahllos
und unabhängig voneinander; alle Elemente müssen die gleiche Chance haben,
ausgewählt zu zu werden)
Im weiteren wird die Bezeichnung ”Stichprobe von Umfang n” verwendet.
Stichprobenwerte: beobachtete Merkmalswerte x1 , x2 , . . ., xn der n Elemente
(Realisierungen der Zufallsvariablen X)
Mathematik III - Folie 48
Häufigkeits- und Verteilungsfunktion einer Stichprobe - ein Beispiel
Beispiel 15.1:
Aus der laufenden Produktion von Gewindeschrauben mit einem Solldurchmesser
von x0 = 5.0 mm wurde eine Stichprobe vom Umfang n = 25 entnommen.
Dabei ergab sich die folgende Urliste (Werte in mm):
4.9; 4.8; 5.0; 5.2; 5.2; 5.1; 4.7; 5.0; 5.0; 4.9; 4.8; 4.9; 5.1; 5.0; 5.0;
5.1; 5.0; 4.9; 4.8; 4.9; 4.9; 5.0; 5.0; 5.1; 5.0
Es treten nur 6 verschiedene Werte auf. Diese lauten der Größe nach geordnet:
4.7; 4.8; 4.9; 5.0; 5.1; 5.2
(jeweils in mm)
Zur Feststellung der absoluten Häufigkeiten ni (i = 1, 2, . . . , 6) dieser Werte dient
die folgende Strichliste:
Stichprobenwert xi (in mm)
ni
4.7
4.8
4.9
5.0
5.1
5.2
|
|||
||||| |
||||| ||||
||||
||
Daraus kann die folgende Verteilungstabelle aufgestellt werden:
xi
mm
4.7
4.8
4.9
5.0
5.1
5.2
ni
1
3
6
9
4
2
hi (= f (xi ))
0.04
0.12
0.24
0.36
0.16
0.08
Mathematik III - Folie 49a
Fortsetzung zu Beispiel 15.1
Mit Hilfe der Formel für die Summenhäufigkeits- oder Verteilungsfunktion
erhält man die folgende Tabelle:
xi
mm
4.7
4.8
4.9
5.0
5.1
5.2
F (xi )
0.04
0.16
0.40
0.76
0.92
1
Grafische Darstellung der Häufigkeitsfunktion bzw. der Verteilungsfunktion:
f (x)
F (x)
6
6
1.0
0.32
0.8
0.24
0.6
0.16
0.4
0.08
0.2
-
4.7 4.8 4.9 5.0 5.1 5.2
x/mm
Häufigkeitsfunktion f (x) (Stabdiagramm)
-
4.7 4.8 4.9 5.0 5.1 5.2
x/mm
Verteilungsfunktion F (x)
Mathematik III - Folie 49b
Gruppierung der Stichprobenwerte bei umfangreichen Stichproben:
ein Beispiel
Aus der laufenden Produktion von Ohmschen Widerständen mit einem Sollwiderstand von 100 Ω wurde eine Stichprobe vom Umfang n = 50 entnommen.
Die Widerstandswerte lagen dabei zwischen xmin = 96.7 Ω und xmax = 104.2 Ω.
Auswahl Intervall I := [96.5 Ω, 104.5 Ω], Einteilung in 8 Klassen der gleichen
Breite 1 Ω ⇒ Klassenmitten sind: 97, 98 ,. . . , 104 (jeweils in Ω)
Es wurde die folgende Verteilungstabelle ermittelt (Urliste nicht mit aufgeführt):
Klassen-Nr. i
Klassengrenzen
(in Ω)
Klassenmitte x̃i
(in Ω)
abs. Klassenhäuf. ni
rel. Klassenhäuf. hi
1
96.5 . . . 97.5
97
2
0.04
2
97.5 . . . 98.5
98
5
0.10
3
98.5 . . . 99.5
99
10
0.20
4
99.5 . . . 100.5
100
13
0.26
5
100.5 . . . 101.5
101
9
0.18
6
101.5 . . . 102.5
102
6
0.12
7
102.5 . . . 103.5
103
4
0.08
8
103.5 . . . 104.5
104
1
0.02
50
1
Σ
Mathematik III - Folie 50a
Grafische Darstellung der Klassenhäufigkeiten in einem Histogramm
Die relativen Klassenhäufigkeiten (siehe Tabelle auf Folie 50a) werden in einem
Histogramm dargestellt:
f (x)
6
0.30
0.20
0.10
-
97
98
99 100 101 102 103 104
x/Ω
In dem Histogramm repräsentiert der Flächeninhalt des i-ten Rechtecks
die relative Klassenhäufigkeit hi der i-ten Klasse (i = 1, 2, . . . , 8).
Mathematik III - Folie 50b
Allgemeine Regeln für die Gruppierung einer umfangreichen Stichprobe
in Klassen
1) Man wähle möglichst Klassen gleicher Breite.
2) Die Klasseneinteilung sollte so gewählt werden, dass die Klassenmitten
durch möglichst einfache Zahlen (z.B. ganze Zahlen) charakterisiert werden.
3) Fällt ein Stichprobenwert in einen der beiden Randpunkte einer Klasse,
so zählt man ihn je zur Hälfte den beiden angrenzenden Klassen zu.
4) Die Festlegung der Anzahl k der Klassen bei n Stichprobenwerten kann
mit Hilfe der folgende Faustregel:
√
k ≈ n für 50 < n < 500
erfolgen. Bei Stichproben mit einem Umfang n > 500 sind höchstens
k = 30 Klassen zu wählen.
Eine weitere häufig empfohlene Faustregel für die Anzahl k der Klassen lautet:
k ≤ 5 · log n.
Mathematik III - Folie 51