Lösungen zum Tutorium in Statistik I: Theoretische Verteilung

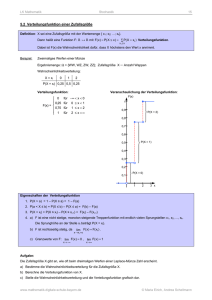
Universität Hannover
Wirtschaftswissenschaftliche Fakultät
Lösungen zum Tutorium in Statistik I:
Theoretische Verteilung
Aufgabe 1
Auszahlung:
Wahrscheinlichkeit:
x 1,2 0
1
P(X=x) 23
3
a) aa)
1,2
2
3
oder
0
1
3
ab) E(X)=0,8
V(X)=0,32
b) E(X) = 0, 8
V (X) = 0, 56
Das Ziel der Risikodiversikation wird verfehlt.
c) ca) S = X1 + X2 + X3
E(S) = 2, 4
cb) Y = 3X
E(Y ) = 2, 4
V (S) = 0, 96
V (Y ) = 9 · V (X) = 2, 88
cc) E(X) = 0, 512
V (X) = 13, 89
Aufgabe 2
a) α = 0, 1
f (x) 6
0.4
0
```
,
,
,
```
```
``
` -
5
x
1
b) ba) P (X = 1) = 0
bb) P (0, 5 ≤ X ≤ 3) = 0, 75
bc) x0,5 = 1, 8377
bb) und bc) lassen sich auch mit Hilfe der Verteilungsfunktion
(
F (x) =
0, 2x2
0≤x≤1
−0, 05x + 0, 5x − 0, 25 1 < x ≤ 5
lösen.
2
c) ca) v = 0, 5401
cb) Ṽ (X) = 1, 193
Aufgabe 3
a) aa)
F(x)
1
6
`
0,75
`
`
`
0,5
`
0,25
p
0
-
1
2
3
4
5
x
ab) P (X > 1) = 0, 6741
b) E(X) = 2
V (X) = 1, 102
c) Z = Anzahl der Teilzeitbeschäftigten aus allen 5 Stichproben
Xi = Anzahl der Teilzeitbeschäftigten in Stichprobe i (i = 1, · · · , 5)
vz = 0, 2347
P
P
Bei Abhängigkeit der Stichproben bleibt E(Z) unverändert, aber V ( Xi ) = V (Xi ) gilt
nicht mehr, so daÿ sich die Varianz verändert. Daraus folgt auch ein veränderter Variationskoezient.
2
Aufgabe 4
a) F (x) = 1 − x−3
x≥1;
,
stetige Zufallsvariable
aa)
F (1) = 1 − 1−3 = 0, lim (F (x)) = 1 − lim (x−3 ) = 1
0
f (x) = F (x) = 3x
x→∞
−4
x→∞
→ f (x) > 0 für x ≥ 1
→ Die Voraussetzungen für eine Verteilungsfunktion sind gegeben.
f(x)
½Z
½
Z
3
p
ab)
1,5
1
x
1
1,5
2
2,5
b) E(X) =
2,5
2
x
f (x)
3
0,5926
0,1875
0,0768
3
2
V (X) =
x0,75 − x0,25 :
3
4
v=
√1
3
√
3
x0,75 = q
4
3 4
x0,25 = 3
⇒ x0,75 − x0,25 = 0, 4868
c) Streuungsmaÿe in b): V (X);
x0,75 − x0,25 ;
vx
• V (Y ) ' 4, 22 · 0, 75 = 3, 165
√
• vy =
V (Y )
E(Y )
;
E(Y ) = 0
→ vy ist nicht deniert (Division durch 0)
• y0,75 − y0,25 = 1
Durch die lineare Transformation wird der Quartilsabstand auf 1 normiert.
3