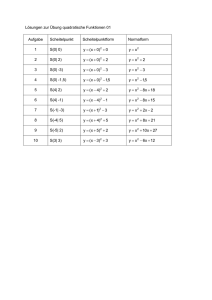
Bearbeitungsvorschlag

MATHEMATISCHES INSTITUT
DER UNIVERSITÄT MÜNCHEN
Dr. E. Schörner
SS 2013
Blatt 10
01.07.2013
Tutorium zur Vorlesung Synthetische und
”
analytische Behandlung geometrischer Probleme“
— Bearbeitungsvorschlag —
37. Wir bestimmen in Abhängigkeit vom Parameter s ∈ R die affine Normalform der
gegebenen Quadrik Qs mit der Gleichung
(∗)
x2 − 4 x y + s y 2 + 2 s x − 4 s y = 0
mit Hilfe quadratischer Ergänzung; dabei ergibt sich
(∗) ⇐⇒
x2 − 4 x y + 2 s x + s y 2 − 4 s y = 0
⇐⇒
x2 + 2 · x · (−2 y) + 2 · x · s + (−2 y)2 + s2 + 2 · (−2 y) · s −
− (−2 y)2 + s2 + 2 · (−2 y) · s + s y 2 − 4 s y = 0
⇐⇒
(x − 2y + s)2 + (s − 4) y 2 = s2 ,
wodurch die folgende Fallunterscheidung motiviert wird:
• Für s = 0 ergibt sich also
(x − 2y)2 − 4 y 2 = 0,
u
x − 2y
=
die affine Normalform u2 − v 2 = 0 eines
so daß man mit
v
2y
sich schneidenden Geradenpaars erhält.
Für s 6= 0 ergibt sich dann
(∗)
1
s−4 2
2
(x
−
2y
+
s)
+
y = 1,
s2
s2
und es folgt:
1
u
(x
−
2
y
+
s)
• Für s = 4 erhält man mit
= s
die affine Normalform
v
y
u2 = 1 eines parallelen Geradenpaars.
1
(x √
− 2 y + s)
u
s
• Für s > 4 erhält man mit
=
die affine Normalform
s−4
v
y
s
u2 + v 2 = 1 einer Ellipse.
1
(x √
− 2 y + s)
u
s
• Für s < 4 und s 6= 0 erhält man mit
=
die affine
4−s
v
y
s
Normalform u2 − v 2 = 1 einer Hyperbel.
38. a) Wir untersuchen in Abhängigkeit vom Parameter a ∈ R \ {0} die affine
Normalform der durch die Gleichung
x2 + 2 a x y + y 2 + 2 y + 1 = 0
gegebenen Quadrik;
x2 + 2 a x y + y 2 + 2 y + 1 = 0
⇐⇒
x2 + 2 x (a y) + (a y)2 − (a y)2 + y 2 + 2 y + 1 = 0
⇐⇒ (x + a y)2 + (1 − a2 )y 2 + 2 y + 1 = 0
Dies motiviert folgende Fallunterscheidung:
Für a2 = 1 ergibt sich für die Quadrik Q
(x + a y)2 + 2 y + 1 = 0 bzw. (x + a y)2 − (−2 y − 1) = 0.
u
x + ay
Mit der Variablentransformation
=
erhält man
v
−2 y − 1
u2 − v = 0
und damit die affine Normalform einer Parabel.
Für a2 6= 1 ergibt sich für die Quadrik Q
1
+
y2 + 2 y ·
1 − a2
2 !
1
−1
1 − a2
2
1 − a2
1 − a2
1
2
2
⇐⇒
· (x + a y) + (1 − a ) ·
y+
= 1.
a2
a2
1 − a2
(x + a y)2 + (1 − a2 ) ·
1
1 − a2
=
• Für 1 − a2 > 0 bzw. 1 > a2 ergibt sich mit der Variablentransformation
q
!
1−a2
·
(x
+
a
y)
u
= 1−aa2 2
,
v
· (y + 1 2 )
|a|
1−a
u2 + v 2 = 1
und damit erhält man die affine Normalform einer Ellipse.
• Für 1 − a2 < 0 bzw. 1 < a2 ergibt sich mit der Variablentransformation
!
1−a2
1
|q
| · (y + 1−a
2)
u
a
=
,
a2 −1
v
· (x + a y)
a2
u2 − v 2 = 1
und damit erhält man die affine Normalform einer Hyperbel.
b) Wir bestimmen die affinen Normalformen der beiden Quadriken
Q1 : x2 + 4 x y + 6 y 2 = 1,
Q 2 : x2 + 6 x y + 4 y 2 = 1
mit Hilfe quadratischer Ergänzung. Wegen
x2 + 4 x y + 6 y 2 = 1 ⇐⇒
x2 + 2 · x · 2 y + 4 y 2 + 2 y 2 = 1 ⇐⇒
⇐⇒ (x + 2 y)2 + 2 y 2 = 1
erhält man mit der Variablentransformation
x√
+ 2y
w
=
z
2y
die affine Normalform w2 + z 2 = 1; damit ist Q1 eine Ellipse.
Wegen
x2 + 6 x y + 4 y 2 = 1 ⇐⇒
x2 + 2 · x · 3 y + 9 y 2 − 5 y 2 = 1 ⇐⇒
⇐⇒ (x + 3 y)2 − 5 y 2 = 1
erhält man mit der Variablentransformation
x√
+ 3y
w
=
z
5y
die affine Normalform w2 − z 2 = 1; damit ist Q2 eine Hyperbel.
Damit beschreiben Q1 und Q2 nicht denselben affinen Typ
39. a) Die in Abhängigkeit der reellen Zahlen a > 0 und b ≥ 0 gegebene Quadrik
x
2
2
2
Q=
∈ R | ax + 2xy + ay − b = 0
y
besitzt die Gleichung
x
x y ·A·
=b
y
mit
A=
a 1
1 a
∈ R2×2 .
Wegen
a − λ
1 det(A − λ E) = = (a − λ)2 − 1 = (1 + a − λ) · (−1 + a − λ)
1
a − λ
für alle λ ∈ R besitzt A die beiden Eigenwerte λ1 = 1 + a und λ2 = −1 + a;
wegen
a − (1 + a)
1
−1 1
1
A − λ1 E =
ist v1 =
1
a − (1 + a)
0 0
1
ein Eigenvektor von A zum Eigenwert λ1 = 1 + a, und wegen
a − (−1 + a)
1
1 1
1
A − λ2 E =
ist v2 =
1
a − (−1 + a)
0 0
−1
ein Eigenvektor von A zum Eigenwert λ2 = −1 + a. Somit besitzt die gegebene Quadrik Q die beiden Hauptachsen
1
1
R · v1 = R ·
sowie R · v2 = R ·
.
1
−1
Mit der orthogonalen Matrix
v2
1 1 1
v1
,
=√
∈ O2 (R)
P =
kv1 k kv2 k
2 1 −1
und der Diagonalmatrix
D = diag (λ1 , λ2 ) =
1+a
0
0
−1 + a
∈ R2×2
x
w
ergibt sich P AP = D, so daß die Variablentransformation
=P·
y
z
die gegebene Gleichung
x
x y ·A·
=b
y
>
in die Gleichung
w
w z · P AP ·
=b
z
>
bzw.
w
w z ·D·
= b,
z
also
(1 + a) · w2 + (−1 + a) · z 2 = b
überführt.
b) Wir bestimmen nun die reellen Zahlen a > 0 und b ≥ 0 für die Q eine Ellipse
bzw. eine Hyperbel darstellt.
• Für a > 1 und b 6= 0 beschreibt Q aufgrund
(1 + a) ·w2 + (−1 + a) ·z 2 = |{z}
b
| {z }
| {z }
>0
>0
>0
der beiden positiven Eigenwerten λ1 = 1 + a und λ2 = −1 + a sowie der
nichtnegativen rechten Seite eine Ellipse.
• Für a ∈ ]0; 1[ und b 6= 0 beschreibt Q aufgrund
(1 + a) ·w2 + (−1 + a) ·z 2 = |{z}
b
| {z }
| {z }
>0
<0
>0
dem positiven Eigenwerten λ1 = 1 + a und dem negativen Eigenwert
λ2 = −1 + a sowie der nichtnegativen rechten Seite eine Hyperbel.
40. a) Die gegebene Quadrik
x
2
2
2
Q=
∈ R | −x + 4 x y + 2 y + 2 x + 8 y − 1 = 0
y
besitzt die Gleichung
x
x
>
x y ·A·
+b ·
+c=0
y
y
mit
−1 2
A=
∈ R2×2 ,
2 2
2
b=
∈ R2
8
und c = −1 ∈ R.
Wegen
−1 − λ
2
= (−1 − λ) (2 − λ) − 22 =
det(A − λ E) = 2
2 − λ
= λ2 − λ − 2 − 4 = λ2 − λ − 6 = (λ − 3) (λ + 2)
für alle λ ∈ R besitzt A die beiden Eigenwerte λ1 = 3 und λ2 = −2; wegen
−4 2
2 −1
1
A − λ1 E =
ist
v1 =
2 −1
0 0
2
ein Eigenvektor von A zum Eigenwert λ1 = 3, und wegen
1 2
1 2
−2
A − λ2 E =
ist
v2 =
2 4
0 0
1
ein Eigenvektor von A zum Eigenwert λ2 = −2. Mit der orthogonalen Matrix
!
√1
√2
−
v2
v1
,
= √25 √1 5 ∈ O2 (R)
P =
||v1 || ||v2 ||
5
5
und der Diagonalmatrix
3 0
D = diag (λ1 , λ2 ) =
∈ R2×2
0 −2
x
u
>
gilt dann P AP = D. Die Variablentransformation
=P·
führt
y
v
nun die gegebene Gleichung
x
x
>
x y ·A·
+b ·
+c=0
y
y
in die Gleichung
u
u
>
u v · P AP ·
+b P ·
+ c = 0,
v
v
>
also
3 0
u
u v ·
·
+ 2 8 ·
0 −2
v
√1
5
√2
5
− √25
√1
5
! u
·
− 1 = 0,
v
und damit
18
4
3 u2 − 2 v 2 + √ u + √ v − 1 = 0
5
5
über. Mit Hilfe quadratischer Ergänzung ergibt sich ferner
2 !
2 !
1
3
3
1
− 2 v2 − 2 · √ · v + √
=
3 u2 + 2 · √ u + √
5
5
5
5
2
2
3
1
=1+3 √
−2 √
5
5
und damit
2
2
3
1
−2 v− √
= 6,
3 u+ √
5
5
!
3
√
u
+
w
5
so daß mit der Variablentransformation
=
die Gleichung
v − √15
z
z2
w2
−
√ 2 √ 2 =1
2
3
entsteht; letztere stellt die euklidische Normalform dar. Damit ist H eine
Hyperbel, und wegen
!
!
w − √35
− √35
x
u
w
=P·
=P·
=P·
+P ·
=
√1
y
v
z + √15
z
5
!
!
√1
√2
√3
−
−
w
w
−1
5
5
5
=P·
+ √2
·
=P·
+
1
1
√
√
z
z
−1
5
5
5
| {z }
3 w2 − 2 z 2 = 6
bzw.
=t
−1
besitzt H den Mittelpunkt t =
sowie die Hauptachsen
−1
−1
1
−1
−2
t + R · v1 =
+R·
und t + R · v2 =
+R·
.
−1
2
−1
1
b) Die Quadrik
x
2
2
2
Q=
∈ R | 2x − 3y = 6
y
besitzt offensichtlich die euklidische Normalform
x2
y2
√ 2 − √ 2 = 1;
3
2
damit ist Q ebenfalls eine Hyperbel und folglich zu H affin äquivalent. Da allerdings Q und H unterschiedliche euklidische Normalformen besitzen, sind
die beiden Hyperbeln nicht metrisch äquivalent.