Universität Konstanz

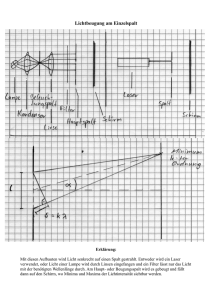
Praktikumsprotokoll:
Lichtstreuung
&
Diffraktive Optik
Robin Marzucca, Andreas Liehl
24. und 31. Mai 2011
Universität Konstanz
1
Inhaltsverzeichnis
1 Einleitung
2 Grundlagen
2.1 Lichtstreuung . . . . . . . . . . .
2.1.1 Rayleigh-Streuung . . .
2.1.2 Mie-Streuung . . . . . . .
2.2 Polarisation . . . . . . . . . . . .
2.2.1 Polarisationsfilterfolie . .
2.2.2 Doppelbrechung . . . . .
2.2.3 Brewster-Winkel . . .
2.3 Beugung . . . . . . . . . . . . . .
2.3.1 Huygenssche Prinzip . .
2.3.2 Beugung am Spalt . . . .
2.4 Geometrische Optik . . . . . . .
2.5 Fresnelsche Zonenplatte . . . .
2.6 Die Flüssigkristallanzeige . . . .
2.7 Eigenschaften von Laserstrahlung
3
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
3
3
4
5
5
7
8
8
9
9
9
11
11
13
14
3 Der Versuch
15
3.1 Versuchsteil 1: Lichtstreuung . . . . . . . . . . . . . . . . . . . . . . . . . . 15
3.2 Versuchsteil 2: Diffraktive Optik . . . . . . . . . . . . . . . . . . . . . . . . 15
4 Auswertung
4.1 Versuchsteil 1: Lichtstreuung . . . .
4.1.1 Statistische Lichtstreuung . .
4.1.2 Dynamische Lichtstreuung . .
4.2 Versuchsteil 2: Diffraktive Optik . .
4.2.1 Abhängigkeit des Drehwinkels
4.2.2 Bestimmung der Pixelgröße .
. . . . . . . . . . . .
. . . . . . . . . . . .
. . . . . . . . . . . .
. . . . . . . . . . . .
von der Wellenlänge
. . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
17
17
17
21
23
23
23
5 Fragen und Antworten
25
5.1 Fragen zum Versuchsteil: Lichtstreuung . . . . . . . . . . . . . . . . . . . . 25
5.2 Fragen zum Versuchsteil: Diffraktive Optik . . . . . . . . . . . . . . . . . . . 27
2
1 Einleitung
In den folgenden beiden Versuchen wollen wir das Phänomen der Lichtstreuung, der Beugung sowie die daraus resultierende Interferenz beobachten. Dazu wird im ersten Versuch
Licht an kleinen Teilchen gestreut und dessen Interferenzmuster und im zweiten Versuch
Bilderzeugung mit einer Flüssigkristallanzeige sowie die Funktionsweise von einem LCD
untersucht.
2 Grundlagen
2.1 Lichtstreuung
Trifft Licht auf ein inhomogenes Medium, so wird es dort gestreut. Dies liegt daran, dass im
inhomogenen Medium Teilchen mit unterschiedlichen Brechzahlen auftreten. Lichtstreuung
ist also ein Phänomen, was uns im Alltag relativ häufig begegnet, da dort viele inhomogene
Medien, wie z.B. Milch, auftreten, wo Licht gestreut werden kann. Dort wird das Licht an
verschiedenen streuenden Teilchen, den sog. Streuzentren, unterschiedlich abgelenkt. Dabei
interferiert das an einem Teilchen gestreute Licht häufig mit Licht, das an einem anderen
Teilchen gestreut wurde. So kommt ein Interferenzmuster zustande. Für den Fall, dass
Licht, welches an benachbarten Teilchen gestreut wurde, miteinander interferiert, ist das
Interferenzmuster zusätzlich überlagert durch das Interferenzbild dieser beiden Lichtwellen. Es handelt sich dabei um ein körniges Interferenzmuster, was man auch als Speckles
bezeichnet. Durch die Bewegung der Teilchen im inhomogenen Medium sind diese Speckles
jedoch nicht statisch sondern weisen eine leichte “Flimmerbewegung“ auf.
Zunächst einmal unterscheidet man bei der Lichtstreuung zwischen der statistischen und
dynamischen Lichtstreuung. Diese beiden Streuungsarten differenzieren dabei nicht unterschiedliche streuende Systeme, sondern betrachten die Lichtstreuung lediglich mathematisch auf unterschiedlicher Ebene.
Bei der statistischen Lichtstreuung betrachtet man ausschließlich das statische Interferenzmuster. Man berechnet die zeitlich gemittelte Streurate an einem Beobachtungspunkt
und es lassen sich anhand dieser Daten Rückschlüsse auf die Beschaffenheit der Streuzentren ziehen.
Bei der dynamischen Lichtstreuung betrachtet man das Interferenzmuster der Speckles. Da dieses dynamisch ist, lassen sich anhand der Bewegungen des Interferenzmusters
Rückschlüsse auf die Geschwindigkeit der Teilchenbewegung im Medium ziehen.
Weiter unterscheidet man zwischen drei Arten der Lichtstreuung, wobei hier die Größe und
Form der Streuzentren die zentrale Rolle spielen. Ist die Größe der Streuzentren deutlich
größer als die Wellenlänge des einfallenden Lichtes, so lässt sich die resultierende Streuung
mit Hilfe der geometrischen Optik berechnen (siehe Abschnitt 2.3f). Für den Fall, dass
die Größe der Streuzentren in etwa vergleichbar mit der Wellenlänge des Lichtes ist, so
lässt sich die Streuung mit der Mie-Streuung (auch Mie-Lorenz-Streuung) berechnen
und für den Fall, dass die Streuzentren deutlich kleiner als die Wellenlänge des Lichtes
sind, sprechen wir von der Rayleigh-Streuung.
3
2.1.1 Rayleigh-Streuung
Für die Rayleigh-Streuung betrachten wir nun Streuzentren für deren Durchmesser d
gilt: d λ. Man erklärt die Rayleigh-Streuung dadurch, dass die Streuzentren durch die
einfallende Lichtwelle ebenfalls zu Schwingungen angeregt werden. Dadurch senden diese
wiederum elektromagnetische Wellen in alle Raumrichtungen aus, wobei dessen Frequenz
gleich der Frequenz der einfallenden Lichtwelle ist. So wird das Licht gestreut. Man bezeichnet die schwingenden Teilchen dann auch als Hertzschen Dipol.
Mathematisch lässt sich die Streuung hier durch den Streuquerschnitt σS beschreiben. Er
wird gebildet aus der zeitmlich gemittelten gestreuten Lichtleistung P S pro Anzahl der
Streuzentren N und Intensität der einfallenden Lichtwelle Ie . Die Definition lautet also:
σS =
PS
N · Ie
Der Streuquerschnitt hat also die Dimension einer Fläche. Anschaulich ist der Streuquerschnitt “ein Maß für die Wahrscheinlichkeit, dass zwischen einer einfallenden Lichtwelle [...]
und einem anderen Teilchen (in unserem Fall das Streuzentrum) [...] ein Streuprozess [...]
stattfindet“ 1 .
Den Streuquerschnitt bei der Rayleigh-Streuung erhält man durch Lösen der Differentialgleichung, die durch die erzwungene Schwingung der Streuzentren gegeben ist. Es ergibt
sich (aus [4]):
σS =
e4
ω4
·
6π · ε20 · m2e · c40 (ω02 − ω 2 )2 + γ 2 ω 2
mit
• e = Elementarladung
• ε0 = Permittivität des Vakuums
• me = Elektronenladung
• c0 = Lichtgeschwindigkeit im Vakuum
• ω = Frequenz des einfallenden Lichtes
• ω0 = Eigenfrequenz der Streuzentren
• γ = Dämpfungskoeffizient
Man kann hier zwei Fälle diskutieren. Zunächst betrachten wir den Fall ω ≈ ω0 . Dann
nimmt der Streuquerschnitt sehr hohe Werte an und man spricht von Resonanz-RayleighStreuung. Genau genommen findet man das Maximum des Streuquerschnitts bei einer
−1/2
2
Frequenz von ω = ω0 · 1 − 2 γ· ω2
.
0
Für den anderen Fall sei ω ω0 . Dann ist σS ∝ ω 4 und damit gilt auch für die gestreute
Intensität:
I ∝ ω4
1
bzw.
I∝
1
λ4
Quelle: http://de.wikipedia.org/wiki/Streuquerschnitt , 04.01.2012
4
Die Intensität ist also sehr stark abhängig von der Wellenlänge.
Dies erklärt beispielsweise die blaue Färbung des Himmels. Trifft Licht in die Atmosphäre,
so wird es dort an den Luftmolekülen gestreut. Da die Eigenfrequenz von Luftmolekülen
jedoch im UV-Bereich liegt (λ0 < 200 nm), gilt ω ω0 . Damit ist die Streuintensität
für eine kürzere Wellenlänge höher und wir sehen überwiegend das blaue gestreute Licht.
Entsprechendes gilt für den roten Abendhimmel. Hier legt das Licht einen langen Weg
durch die Atmosphäre zurück, währenddessen das blaue Licht herausgestreut wird und
vom Beobachter nur das langwellige rote Licht wahrgenommen wird. Dies veranschaulicht
Abbildung (1).
Abbildung 1: Die Skizze veranschaulicht die Streuung des Lichtes in der Atmosphäre. Dabei wird im linken Bild tagsüber das blaue Licht stärker gestreut, sodass
der Himmel blau erscheint. Im rechten Bild wurde das blaue Licht bereits
herausgestreut bevor es zum Beobachter gelangt.
2.1.2 Mie-Streuung
Für den Fall, dass für den Durchmesser d der Streuzentren gilt: d ≈ λ, ist die mathematische Betrachtung der Streuung deutlich komplizierter, weshalb wir an dieser Stelle nicht
näher darauf eingehen wollen.
Physikalisch werden die Teilchen wieder zu Schwingungen angeregt, d.h. es bilden sich wieder Hertzsche Dipole. Allerdings liegen durch die Größe der Teilchen viele Dipole direkt
nebeneinander, die miteinander interferieren, was die Berechnung recht aufwendig macht.
Die resultierende Streuung ist dabei sehr stark abhängig von der Größe und der Oberflächenbeschaffenheit der Streuzentren. Weiter sei bei der Mie-Streuung vorausgesetzt, dass
die Streuzentren eine sphärische Form besitzen.
Ein weiterer entscheidender Unterschied zur Rayleigh-Streuung erhalten wir in der Intensitätsverteilung im Raum. Während die Hertzschen Dipole bei der Rayleigh-Streuung
in alle Richtungen gleichmäßig abstrahlt, interferiert die Strahlung der Hertzschen Dipole
bei der Mie-Streuung mit der einfallenden Lichtwelle. Dadurch ist die Intensität für kleine
Streuwinkel deutlich höher.
2.2 Polarisation
Für gewöhnlich unterscheidet man elektromagnetische Wellen durch Betrachtung von Wellenlänge, Amplitude oder Phasenverschiebung. Wir können aller-
5
dings auch die Ebenen betrachten, in denen sie schwingen. Dabei bezeichnet
man als Schwingungsebene per Konvention die Ebene, in der sich das elektrische
Feld ausbreitet. Von der Sonne ausgestrahltes Licht ist zunächst unpolarisiert,
die einzelnen Lichtwellen haben also keine spezifische Ausrichtung und das Licht
schwingt in jeder Ebene. Bei Ankunft auf der Erde stellt man allerdings fest,
dass das Licht teilpolarisiert ist, was auf Streuung an Luftteilchen zurückzuführen ist. Bei der Polarisation von Licht unterscheidet man grundsätzlich drei
verschiedene Fälle: linear, zirkular und elliptisch polarisiertes Licht. Die Schwingungsebene linear polarisierten Lichtes ist dabei zeitlich konstant, während sie
sich bei zyklisch oder elliptisch polarisiertem Licht zeitlich ändert:
Abbildung 2: Vergleich unterschiedlich polarisierter Wellen[Wik11]
Um die einzelnen Fälle genauer betrachten zu können teilen wir das elektrische
Feld der Welle zunächst in zwei Komponenten, Ex und Ey auf, die nur in x- bzw.
in y-Richtung schwingen. Weiter nehmen wir eine ebene monochromatische
Welle an. Unsere E-Welle hat also die Form:




Ex
0
~ =E
~x + E
~ y =  0  · ei(kz−ωt) +  Ey  · ei(kz−ωt+ϕ)
E
0
0
Die Welle expandiert damit nur in z-Richtung.
Die Art der Polarisation hängt jetzt nur noch von der Phasenverschiebung ϕ
6
ab. Linear polarisiertes Licht erhalten wir für eine Phasenverschiebung von
ϕ = 0 oder ϕ = π, zirkular polarisiertes Licht für ϕ = ± π2 und elliptisch
polarisiertes Licht für jede Phasenverschiebung dazwischen. Voraussetzung für
zirkular polarisiertes Licht ist außerdem, dass die beiden Amplituden Ex und
Ey betragsmäßig gleich sind.
2.2.1 Polarisationsfilterfolie
Eine Möglichkeit, Licht linear zu polarisieren ist die Verwendung einer Polarisationsfilterfolie. Dabei besitzt das Material der Folie eine spezielle atomare
Struktur, welche die E-Feld Komponente des Lichtes und damit auch die Lichtwelle insgesamt absorbiert. Bildhaft könnte man sich eine Folie vorstellen, die
aus vielen extrem feinen Gitterstäben besteht und nur die senkrechte Komponente transmittiert.
Abbildung 3: Prinzip der Drahtgitterpolarisation[Wik11]
Zur näheren Betrachtung des Effekts betrachten wir bereits polarisiertes Licht,
das auf ein solches Drahtgitter trifft. Drehen wir das Drahtgitter so, dass die
Gitterstäbe parallel zur Schwingungsebene der Welle liegen, so wird beim Auftreffen der Welle auf das Gitter durch das elektrische Feld der Welle eine
Schwingung der Elektronen im Draht erzwungen. Dadurch verhält sich der
Gitterstab wie ein elektrischer Dipol und sendet auch eine elektromagnetische
Welle aus, die sich in der gleichen Ebene - jedoch gegenphasig - hinter dem
Gitter ausbreitet. Dadurch wird die ursprüngliche Welle hinter dem Polarisationsfilter ausgelöscht. Vor dem Gitter laufen die beiden Wellen allerdings in
Phase, was dazu führt, dass das Licht, das auf den Polarisationsfilter trifft,
reflektiert wird. Dieses Prinzip löscht sämtliche Schwingungskomponenten, die
nicht senkrecht auf dem Gitter stehen, aus.
7
2.2.2 Doppelbrechung
Die Doppelbrechung ist ein Phänomen, das in optisch anisotropen Medien vorkommt. Das Medium besitzt dabei für verschiedene Schwingungsrichtungen
unterschiedliche Brechzahlen. Insbesondere tritt dieses Phänomen bei kristallinen Medien auf, deren Kristallgitter in verschiedene Richtungen unterschiedlich
dicht ist.
Man unterscheidet dabei zusätzlich zwischen optisch einachsigen und optisch
zweiachsigen Materialien, wobei Ersteres nur zwei und Letzteres drei verschiedene Brechungsindizes besitzt.
Für solche Medien lässt sich ein sogenanntes Indexellipsoid (Abb. 4) zeichnen,
welches den Brechungsindex für Felder in verschiedene Richtungen angibt. Das
Indexellipsoid kann bis zu drei verschiedene Hauptachsen haben.
Um das Verhalten von Wellen in einem solchen Medium zu erklären, unterscheidet man zwischen einem ordentlichen und einem außerordentlichen Strahl.
Der ordentliche Strahl schwingt dabei immer senkrecht zur optischen Achse des
Mediums und verhält sich gemäß dem Snelliusschen Brechungsgesetz. Der außerordentliche Strahl schwingt senkrecht zum ordentlichen Strahl in der Ebene,
die durch die optische Achse und die ursprüngliche Propagationsrichtung aufgespannt wird. In einem biaxialen Medium sind für gewöhnlich beide Strahlen
außerordentlich.
Abbildung 4: Indexellipsoid eines uniaxialen Kristalles. [Wik]
Durch geschicktes einstellen des Winkels, unter dem das Licht einfällt, kann
erreicht werden, dass der ordentliche Strahl das Medium direkt wieder verlässt, während der außerordentliche Strahl totalreflektiert wird. Das austretende Licht ist also linear polarisiert.
[Sacc]
2.2.3 Brewster-Winkel
Bei der Reflexion von Licht an einem Medium mit Brechzahl n wird gemäß den Fresnelschen Formeln immer ein Teil des Lichtes transmittiert und ein Teil reflektiert. Der
schottische Physiker Sir David Brewster zeigte bei seinen Untersuchungen empirisch, dass
8
reflektiertes Licht total polarisiert ist, wenn der Winkel zwischen reflektiertem und transmittiertem Licht genau 90◦ beträgt. Der Einfallswinkel unter dem dieses Phänomen auftritt
wird Brewsterwinkel genannt. In diesem Fall werden die senkrechten Anteile des Lichtes
gebrochen, während die parallelen Anteile komplett reflektiert werden. Der Brewsterwinkel
berechnet sich über den Zusammenhang ΘB = arctan(n)2 .
2.3 Beugung
Eines der wichtigsten Phänomene von Licht ist die sog. Beugung. Sie tritt an
Hindernissen wie z.B. Blenden oder Spalten auf. Die Erklärung für dieses Phänomen beruht auf dem Huygensschen Prinzip.
2.3.1 Huygenssche Prinzip
Das nach seinem Entdecker benannte Huygenssche Prinzip beschreibt die Ausbreitung von Wellen auf elementarer Ebene. Es besagt, dass sich von jedem
Punkt auf einer Wellenfront eine Elementarwelle, eine halbkugelförmige Welle,
in Propagationsrichtung ausbreitet. Die Wellenfront, die sich nach einer kleinen Zeitspanne ∆t um den Ort ∆x fortbewegt hat, erhält man schließlich durch
Superposition aller Elementarwellen.
Mit Hilfe dieses Prinzips lassen sich einige Welleneigenschaften des Lichtes erklären. Eine wichtige Eigenschaft hierbei ist die Brechung. Für Licht, dass auf
eine Grenzfläche zwischen zwei Medien trifft, gilt dabei das Snelliussche Brechungsgesetz:
n1 · sin(α) = n2 · sin(β)
(1)
wobei n1 und n2 die beiden Brechungsindizes der Medien und α und β die Winkel, in der das Licht auf die Grenzfläche trifft bzw. diese verlässt, bezeichnen3 .
Man kann sich diesen Zusammenhang auch anschaulich klarmachen. In Abb.
(5)4 erkennt man eine Welle, die auf eine Grenzfläche trifft. An der Grenzfläche
breiten sich nun Elementarwellen aus. Da diese sich jedoch langsamer (bzw. je
nach Brechnungsindex schneller) ausbreiten als Licht, dass noch nicht auf die,
Grenzfläche getroffen ist, wird das Licht gebrochen.
2.3.2 Beugung am Spalt
Treffen ebene Lichtwellen auf eine Blende, bzw. einen Spalt, so wird das Licht
dahinter gebeugt. Dieses Phänomen beruht ebenfalls auf dem Huygensschen
Prinzip. Es breiten sich hinter dem Spalt halbkugelförmige Elementarwellen
aus. Betrachtet man die räumliche Ausdehnung des Spaltes als einen einzigen
Punkt, so breiten sich die Elementarwellen auch nur an diesem Punkt aus und
2
aus dem eigenen Versuchsprotokoll zu den Versuchen Fresnelsche Formeln und Hochfrequenzsignale
Streng genommen misst man hier nicht den Winkel zwischen Lichtstrahl und Grenzfläche, sondern
zwischen Lichtstrahl und Lot auf Letztere.
4
Quelle: http://www.phylex.de/data/pic/snellgesetz/wellenfront.png , 03.01.2012
3
9
Abbildung 5: Veranschaulichung des Snelliusschen Brechungsgesetzes
man erhält hinter der Blende anstatt ebenen Wellen, halbkugelförmige Wellen.
Dieses veranschaulicht Abbildung (6)5 .
Das Phänomen der Beugung wird mathematisch durch das Kirchhoffsche
Beugungsintegral beschrieben, auf dessen Erläuterung an dieser Stelle jedoch
verzichtet wird, da es zum Verständnis nicht weiter beiträgt.
Bei der Beobachtung des Verhaltens der gebeugten Lichtwelle hinter dem Spalt
wird zwischen zwei Beugungsarten unterschieden.
Die Fraunhofersche Beugung idealisiert die Beobachtung in soweit, dass nur
das Fernfeld, d.h. das Beugungsmuster in großem Abstand zum Spalt, betrachtet wird. Ebenso befindet sich auch die Lichtquelle in großem Abstand zur
Blende. Da es im Versuch jedoch relativ schwierig und vor allem fehleranfällig
wäre, einen großen Abstand zwischen Lichtquelle, Spalt und Schirm einzuhalten, wird hinter dem Spalt eine Sammellinse angebracht. Diese bündelt alle in
einer Richtung verlaufenden parallelen Lichtstrahlen in ihrer Brennebene. Die
Fraunhofersche Beugung eignet sich gut, da hier das Beugungsmuster mathematisch relativ einfach zu berechnen ist.
Im Gegensatz zur Fraunhoferschen Beugung beschreibt die Fresnelsche
Beugung das Beugungsmuster im Nahfeld, d.h. die Abstände zwischen Licht5
Quelle: http://www.pi1.uni-stuttgart.de/teaching/Vorlesungsversuche/Bilder/B428_1.jpg , 03.01.2012
Abbildung 6: Die Abbildung veranschaulicht die Lichtbeugung am Spalt unter der Idealisierung, dass der Spalt nur aus einem Punkt besteht.
10
quelle, Spalt und Beobachtungsschirm sind relativ klein. Dies macht die mathematische Berechnung deutlich aufwändiger, da der Gangunterschied nicht mehr
einfach über trigonometrische Winkelbeziehungen (siehe auch Abschnitt 2.3.1)
berechnet werden kann. Die resultierenden Beugungsmuster unter Berechnung
mittels Fraunhoferschen Beugung bzw. Fresnelschen Beugung, sowie die
Übergangsbereiche dazwischen zeigt Abbildung (7).
Abbildung 7: Beugung am Spalt: Übergang von Fraunhoferscher Beugung für große
Abstände (a) zu Fresnelscher Beugung bei kleinen Abständen (d) [1].
[Beug]
2.4 Geometrische Optik
Die geometrische Optik ergibt sich als Grenzfall der Optik für ω → ∞, sodass die Wellenlänge des Lichtes verschwindet. Sie findet Anwendung bei der Behandlung optischer
Systeme, bei denen die Details der Objekte im Vergleich zur Wellenlänge des Lichtes groß
sind. Für die geometrische Optik gelten folgende Grundvoraussetzungen:
• Lichtstrahlen sind geradlinig und unterliegen dem Superpositionsprinzip,
• es greift das Fermatsche Prinzip,
• das Reflexionsgesetz gilt,
• das Snelliussche Brechungsgesetz gilt,
• Licht breitet sich in einem optischen Medium der Brechzahl n mit der Geschwindigkeit v = nc aus.
2.5 Fresnelsche Zonenplatte
Eine Fresnelsche Zonenplatte ist eine Platte, auf der konzentrische Ringe gewisser Breite
ausgeschnitten wurden, wodurch es hinter der Zonenplatte zu konstruktiver Interferenz der
Strahlen und somit zu einer Verstärkung des Lichtes im Brennpunkt kommt. Wahlweise
können die undurchlässigen Ringe der Fresnelschen Zonenplatte auch durch ein Medium
11
ersetzt werden, welches eine Phasenverschiebung von ϕ = π verursacht, wodurch auch diese
Strahlen konstruktiv interferieren.
Um einen Zusammenhang, zwischen den einzelnen Zonen und ihrer Breite zu finden, betrachten wir zunächst mit Hilfe von Abb. 8 den Gangunterschied zwischen einem Strahl,
der durch einen der Ringe läuft und einem Strahl, der unabgelenkt durch die Mitte der
Zonenplatte läuft.
Abbildung 8: Zusammenhang zwischen Gangunterschied d, Winkel ϕ und der Gitterkonstanten g bei der Beugung am Gitter
Da wir für eine Verstärkung der Intensität die destruktiv interferierenden Strahlen eliminieren müssen, folgt:
p
p
λ
rn2 + g 2 − g +
rn2 + f 2 − f = n
2
(2)
Daraus ergibt sich für rn :
p
nλ(4g + nλ)(4f + nλ)(4f + 4g + nλ)
rn =
8(f + g) + 4nλ
(3)
Entwickelt man rn nach einer Näherung für λ f , so erhält man:
s
rn ≈
nλ ·
f ·g
f +g
(4)
Die Breite der abwechselnd durchlässigen und nicht durchlässigen Ringe ergibt sich über
den Zusammenhang
s
f · g g→∞ p
rn = nλ
=
nλf
(5)
f +g
wobei n ∈ N, λ die Wellenlänge, f die Brennweite und g die Gegenstandsweite bezeichnen.
Fresnelsche Zonenplatten werden vor Allem verwendet, um Röntgenstrahlen zu bündeln,
da Röntgenlinsen sehr ineffizient sind.
12
Abbildung 9: Bild einer binären Fresnelschen Zonenplatte. [Wik11]
2.6 Die Flüssigkristallanzeige
Eine monochromatische Flüssigkristallanzeige besteht wie in Abb. 10 aus einer Einheit aus
zwei Glasplatten, zwischen denen sich ein Flüssigkristall mit Elektroden befindet, sowie
aus zwei Polarisatoren vor und hinter dieser Einheit, die zu 90◦ gedreht angeordnet sind.
Abbildung 10: Aufbau einer einfachen Flüssigkristallanzeige[FK]
In diesem Fall wird in der Anzeige eine nematische Drehzelle verwendet. In der nematischen
Drehzelle befindet sich ein Flüssigkristall, dessen Moleküle an den Enden der Zelle einen
Winkel von 90◦ zueinander aufweisen und dazwischen eine kontinuierliche Drehung beschreiben. Durchdringt ein Lichtstrahl die Zelle, folgt die Polarisationsrichtung des Lichtes
der Ausrichtung der Moleküle und wird somit um 90◦ gedreht. Beim Anlegen einer Spannung an die nematische Drehzelle orientieren sich die Moleküle entlang des magnetischen
13
Feldes, was dazu führt, dass die Polarisationsrichtung des Lichtes nicht mehr beeinflusst
wird und das Licht somit vom zweiten Polarisator vollständig absorbiert wird. (Siehe dazu
auch Abb. 11)
Abbildung 11: Aufbau einer einfachen Flüssigkristallanzeige[Wik11]
2.7 Eigenschaften von Laserstrahlung
Das Licht eines Lasers eignet sich für diesen Versuch auf Grund seiner besonderen Eigenschaften sehr gut:
• Es ist monochromatisch, der Laser strahlt also nur Licht einer einzigen Wellenlänge
aus.
• Es ist parallel, die Breite des Strahls ändert sich daher auch auf große Entfernungen
praktisch nicht.
• Es ist kohärent. Der Gangunterschied, einzelner Lichtwellen ist gleich null.
• Da bei der Erzeugung eines Laserstrahls oft polarisierende Teile verwendet werden,
ist sein Licht häufig linear polarisiert.
• Außerdem besitzt das Licht eines Lasers eine sehr hohe Intensität.
14
3 Der Versuch
3.1 Versuchsteil 1: Lichtstreuung
Abbildung (12)6 zeigt eine Skizze unseres Versuchsaufbaus. Das vom Laser emittierte Licht
wird durch eine Sammellinse auf die Probe, die auf einem Objektträger aufgetragen ist,
fokussiert. Das dadurch entstehende Interferenzmuster wird auf dem Schirm, einem Blatt
Papier, sichtbar.
Im ersten Versuchsteil soll die statistische Lichtstreuung untersucht werden. Dazu wird das
Interferenzmuster, welches eine Form von konzentrischen Ringen aufweist, von 3 Proben
untersucht: einer Silica-Lösung mit Teilchendurchmesser dS = 3, 01 µm und zwei LatexLösungen mit Teilchendurchmessern dL1 = 1, 5 µm und dL2 = 4, 6 µm. Für jedes Interferenzmuster wird auf dem Schirm das Hauptmaximum und die Lage der Maxima, die noch
eindeutig zu erkennen sind, aufgezeichnet, woraus sich später der Ablenkwinkel ergibt.
Hierzu ist außerdem der Abstand der Probe zum Schirm notwendig, der bei jeder Probe
ebenfalls vermessen wurde.
Im zweiten Versuchsteil soll die dynamische Lichtstreuung untersucht werden. Dazu wurde mit einem Detektor das Intensitätsspektrum des Speckle-Musters aufgezeichnet und
gespeichert. Aus diesen Daten soll später die dynamische Lichtstreuung qualitativ untersucht werden.
Abbildung 12: Die Skizze zeigt den Versuchsaufbau beim Versuch Lichtstreuung.
3.2 Versuchsteil 2: Diffraktive Optik
Im Versuch Diffraktive Optik soll die Funktionsweise einer monochromatischen Flüssigkristallanzeige untersucht werden. Wir stellen dafür zunächst einen Einzelspalt mit einer
Breite von 100 Pixeln auf dem Schirm dar und beleuchten diesen. Anschließend wird die
Ausrichtung des Analysators gedreht, um die Winkel zu suchen, unter denen der größte
6
Quelle: Benedikt Wigger, Aaron Riede: Protokoll zum Physikalischen Anfäangerpraktikum III - Lichtstreuung und Diffraktive Optik , 12.12.2011
15
Kontrast auftritt, wobei der Polarisator stets bei einem Winkel von -90◦ stand. Den größten
Kontrast erhielten wir für die Winkelstellungen 90◦ , -5◦ und -68◦ am Analysator, wobei in
den beiden äußeren Fällen der Spalt dunkel und umgekehrt bei einer Analysatorstellung
von -5◦ der Spalt hell war. Dabei fiel auf, dass der Spalt stets noch zu erahnen war. Selbst
wenn die Intensität im Spalt und außerhalb nahezu gleich waren erschien der Rand des
Spaltes dunkel.
Nun sollte die wellenlängenabhängige Drehung der Polarisationsebene untersucht werden.
Dazu wurde ein Aufbau wie in Abb. 13 verwendet. Als Lichtquellen wurden hier ein Laser
mit Wellenlänge λ = 532nm, sowie eine blaue, eine rote und eine gelbe LED-Lampe verwendet. Für jede dieser Wellenlängen wurde die Intensität mit Hilfe eines Detektors in 10◦
Schritten der Analysatorstellung von -90◦ bis 90◦ untersucht:
Abbildung 13: Die Skizze zeigt den Versuchsaufbau beim Versuch Diffraktive Optik zur
Untersuchung der wellenlängenabhängigen Drehung der Polarisationsebene.
Zur Bestimmung der Pixelgröße des SLM wurde drei Messungen vorgenommen. Zunächst
wurde ein Quadrat mit 400 x 400 Pixeln auf dem SLM angezeigt und abgebildet. Dabei
wurde ein Aufbau nach Abb. 14 verwendet. Gemessen wurde die Bildweite b = 40, 0(5)cm
und die Kantenlänge a = 6, 6(1)cm des Bildes. Die Linse hatte eine Brennweite von f =
65mm.
Abbildung 14: Die Skizze zeigt den Versuchsaufbau beim Versuch Diffraktive Optik zur
geometrischen Bestimmung der Pixelgröße des SLM.
Eine diffraktive Möglichkeit zur Bestimmung der Pixelgröße besteht darin, mit dem Laser
den SLM zu beleuchten und das Licht mit einer Sammellinse (f = 200mm) zu bündeln.
Dabei entsteht auf dem Schirm ein Beugungsmuster. Gemessen wurde von diesem Muster
das Maximum 2. Ordnung (r2 = 6, 75(50)mm) und das Maximum 5. Ordnung (r5 =
16, 5(5)mm).
16
Tabelle 1: Normierte Messwerte zur Bestimmung der Wellenlängenabhänigkeit der Drehung der Polarisationsebene
α [◦ ]
-90
-80
-70
-60
-50
-40
-30
-20
-10
0
10
20
30
40
50
60
70
80
90
ULaser
Umax
Urot
Umax
Ublau
Umax
Ugelb
Umax
0,112(12)
0,036(12)
0,014(12)
0,052(12)
0,147(12)
0,292(12)
0,451(12)
0,625(12)
0,781(12)
0,907(12)
0,983(12)
1,000(12)
0,960(12)
0,857(12)
0,715(12)
0,546(12)
0,385(12)
0,228(12)
0,102(12)
0,535(27)
0,417(27)
0,299(27)
0,235(27)
0,214(27)
0,251(27)
0,326(27)
0,433(27)
0,572(27)
0,738(27)
0,845(27)
0,920(27)
0,984(27)
1,000(27)
0,963(27)
0,882(27)
0,775(27)
0,647(27)
0,508(27)
0,457(22)
0,448(22)
0,470(22)
0,535(22)
0,617(22)
0,713(22)
0,813(22)
0,878(22)
0,948(22)
0,991(22)
1,000(22)
0,974(22)
0,917(22)
0,826(22)
0,730(22)
0,639(22)
0,539(22)
0,470(22)
0,448(22)
0,510(29)
0,382(29)
0,304(29)
0,275(29)
0,304(29)
0,353(29)
0,451(29)
0,569(29)
0,706(29)
0,794(29)
0,902(29)
0,971(29)
1,000(29)
0,980(29)
0,912(29)
0,794(29)
0,676(29)
0,549(29)
0,441(29)
Letztlich sollte die Pixelgröße noch mit einer weiteren diffraktiven Methode bestimmt werden: Dazu wird auf dem SLM eine Fresnelsche Zonenplatte mit r1 = xPixel, x ∈ (10..25)
abgebildet und ihre Brennweite bestimmt.
Tabelle 2: Wertetabelle zur Messung der Brennweite b in Abhängigkeit vom Radius r1 der
innersten Fresnelschen Zone
r1 [Pixel]
b [cm]
10
18,5(5)
15
42,5(5)
20
72,0(5)
12
28,5(5)
25
103,0(5)
4 Auswertung
4.1 Versuchsteil 1: Lichtstreuung
4.1.1 Statistische Lichtstreuung
Zunächst wollen wir die statistische Lichtstreuung untersuchen. Dazu berechnen wir den
Streuwinkel α unter dem die einzelnen Minima und Maxima auf dem Schirm auftreten. Die
17
Berechnung des Winkels kann man sich anhand Abbildung (12) herleiten. Es gilt dann:
s
α = arctan
h
wobei hier h die Höhe der Probe über dem Schirm und s der Abstand zwischen Hauptmaximum und betrachtetem Minimum/Maximum ist. Der Fehler berechnet sich dann durch7 :
s
δα =
=
2 2
∂α
∂α
· δs +
· δh
∂s
∂h
q
1
· (h · δs)2 + (s · δh)2
s 2 + h2
Tabelle (3) zeigt die von uns gemessenen und berechneten Werte für die einzelnen Proben.
Silica-Probe mit d = 3, 01 µm und h = (11, 9 ± 0, 2) cm
Ordnung smax [cm] smin [cm]
αmax [◦ ]
αmin [◦ ]
1
2,1
1,1 10,0 ± 0,9
5,3 ± 1,0
2
4,0
3,1 18,6 ± 0,9 14,6 ± 0,9
3
6,7
5,6 29,4 ± 0,8 25,2 ± 0,9
Latex-Probe mit d = 1, 5 µm und h = (9, 0 ± 0, 2) cm
Ordnung smax [cm] smin [cm]
αmax [◦ ]
αmin [◦ ]
1
5,5
4,2 31,4 ± 1,1 25,0 ± 1,2
Latex-Probe mit d = 4, 6 µm und h = (18, 2 ± 0, 2) cm
Ordnung smax [cm] smin [cm]
αmax [◦ ]
αmin [◦ ]
1
3,6
2,2 11,2 ± 0,6
6,9 ± 0,6
2
6,6
5,3 19,9 ± 0,6 16,2 ± 0,6
3
9,8
8,2 28,3 ± 0,6 24,3 ± 0,6
4
13,5
11,7 36,6 ± 0,5 32,7 ± 0,5
Tabelle 3: Die Tabelle zeigt die Streuwinkel der Maxima und Minima der einzelnen Proben.
Dabei gilt generell δsmax = δsmin = 0, 2 cm.
Nun wollen wir den ursprünglichen Streuwinkel in der Probe berechnen. Da das gestreute Licht beim Austritt aus der Probe gebrochen wird, erhalten wir den ursprünglichen
Streuwinkel über das Snelliussche Brechungsgesetz (Gleichung (1)). Dabei gilt für den
Brechungsindex der Probe der Brechungsindex von Wasser nW = 1, 336 und für den Brechungsindex von Luft nL ≈ 1. Es ist hier nicht erforderlich mit dem exakten Brechungsindex von Wasser zu rechnen, da dieser sich von 1 nur minimal unterscheidet, wodurch sich
die Werte nicht über die von uns ohnehin schon angenommenen Unsicherheiten unterscheiden würden. Es gilt damit für den ursprünglichen Streuwinkel:
1
θ = arcsin
· sin(α)
nW
7
Sofern nicht anders angegeben berechnet sichrim Folgenden der Fehler für eine Messgröße X mit fehler2
P ∂X
behafteten Größen xi generell durch δX =
.
i ∂xi · δxi
18
und für dessen Fehler:
cos(α)
δθ = q
· δα
n2W − sin2 (α)
Tabelle (4) zeigt die von uns gemessenen und berechneten Werte für die einzelnen Proben.
Silica-Probe mit d = 3, 01 µm und h = (11, 9 ± 0, 2) cm
Ordnung
αmax [◦ ]
αmin [◦ ]
1
7,5 ± 0,7
4,0 ±
0,7
2
13,8 ± 0,7 10,9 ±
0,7
3
21,5 ± 0,6 18,6 ±
0,6
Latex-Probe mit d = 1, 5 µm und h = (9, 0 ± 0, 2) cm
Ordnung
αmax [◦ ]
αmin [◦ ]
1
23,0 ± 0,8 18,5 ±
0,8
Latex-Probe mit d = 4, 6 µm und h = (18, 2 ± 0, 2) cm
Ordnung
αmax [◦ ]
αmin [◦ ]
1
8,4 ± 0,5
5,2 ±
0,5
2
14,8 ± 0,4 12,1 ±
0,4
3
20,8 ± 0,4 17,9 ±
0,4
4
26,5 ± 0,3 23,9 ±
0,4
Tabelle 4: Die Tabelle zeigt die ursprünglichen Streuwinkel der Maxima und Minima der
einzelnen Proben.
Zuletzt wollen wir die Streuung der Teilchen simulieren. Dazu verwenden wir die Software MiePlot v4211. Dieses simuliert bei gegebener Wellenlänge λ, Brechungsindizes n von
Streu- und umgebendem Medium und Teilchendurchmesser d das Interferenzmuster der
Mie-Streuung. Für jede Probe wird ein solches Bild, wobei wir den Teilchendurchmesser variieren, sodass eine möglichst genaue Übereinstimmung mit den von uns gemessenen
Winkeln gegeben ist. Abbildungen (15), (16) und (17) zeigen die von uns simulierten Streuungen. Dabei sind jeweils die von uns berechneten Winkel für die Minima (rot) und Maxima (grün) nach Tabelle (4), sowie deren Unsicherheit in das Diagramm mit eingetragen.
Tabelle (5) zeigt die von uns vermuteten Teilchendurchmesser, sowie deren prozentuale
Abweichung zum angegebenen Wert.
Probe
Silica
Latex
Latex
gegebenes d [µm]
3,01
1,50
4,60
vermutetes d [µm]
2,7
1,5
4,4
proz. Abweichung
10,3%
0%
4,3%
Tabelle 5: Die Tabelle vergleicht die angegebenen Teilchendurchmesser und die von uns
vermuteten anhand unserer Berechnungen der Streuwinkel und Simulation der
Streuung.
19
Abbildung 15: Das Diagramm zeigt die simulierte Streuung für Licht der Wellenlänge λ =
532 nm in einer Silica-Lösung mit von uns vermutetem Teilchendurchmesser
dS = 2, 7 µm. Die senkrechten Balken rechts und links der Mittelbalken
geben jeweils die Unsicherheit an.
Abbildung 16: Das Diagramm zeigt die simulierte Streuung für Licht der Wellenlänge λ =
532 nm in einer Latex-Lösung mit von uns vermutetem Teilchendurchmesser
dL1 = 1, 5 µm. Die senkrechten Balken rechts und links der Mittelbalken
geben jeweils die Unsicherheit an.
20
Abbildung 17: Das Diagramm zeigt die simulierte Streuung für Licht der Wellenlänge λ =
532 nm in einer Latex-Lösung mit von uns vermutetem Teilchendurchmesser
dL1 = 4, 6 µm. Die senkrechten Balken rechts und links der Mittelbalken
geben jeweils die Unsicherheit an.
Fehlerbetrachtung Vor allem bei den Messungen mit den Latex-Proben ließ sich der
Teilchendurchmesser der Streuzentren relativ gut bestätigen. Bei der Silica-Probe war leider
kein eindeutiges Interferenzmuster zu simulieren, sodass unsere berechneten Werte mit der
Simulation in Einklang bringen zu sind. Trotz recht guter Übereinstimmung treten auch
bei der Latex-Probe Abweichungen auf.
Verantwortlich hierfür sind vermutlich Fehler in der Messgenauigkeit, so war es relativ
schwierig beim Interferenzmuster exakt das Minimum bzw. Maximum zu bestimmen, da
diese kontinuierlich ineinander übergingen. Weiter wurde das Spektrum, das am besten
mit den von uns berechneten Werten übereinstimmt lediglich nach Augenmaß und ohne
weitere technische Hilfsmittel bestimmt. Hier könnten weitere Fehlerquellen liegen.
Ein weiterer Aspekt, der in unseren Rechnungen nicht berücksichtigt wurde ist, dass bei
der Mie-Streuung die Teilchen als kugelförmig angenommen werden, jedoch ist dies in
der Realität in der Regel nicht der Fall. Ebenso konnte nicht festgestellt werden, ob die
verwendeten Proben evtl. verunreinigt waren, was zu weiteren Fehlern führt.
Abschließend lässt sich jedoch sagen, dass der Versuch - mit ein wenig mehr technischen
Hilfsmitteln - sehr gut geeignet ist, um die statistische Lichtstreuung zu untersuchen.
4.1.2 Dynamische Lichtstreuung
Im zweiten Versuchsteil wollen wir die dynamische Lichtstreuung untersuchen. Die von uns
aufgezeichneten Diagramme, die für die Proben aufgenommen wurden und die Amplitude
in Abhängigkeit der Frequenz auftragen, sind für die Silica-Probe und die Latex-Probe
mit Teilchendurchmesser d = 1, 5 µm in Abbildungen (18) und (19) dargestellt. Auf das
21
Diagramm der anderen Latex-Probe wurde hier verzichtet, da dort leider ebenso nichts zu
erkennen ist, wie auf den beiden anderen. Das Prinzip dieser Messmethode beruht darauf,
im Spektrum Peaks zu lokalisieren um daraus die Teilchengeschwindigkeit der Streuzentren
zu ermitteln. Dies ist in diesen Diagrammen nur mit sehr viel Phantasie möglich, was uns
als so stark fehleranfällig erscheint, dass an dieser Stelle darauf verzichtet wird.
Abbildung 18: Das Diagramm zeigt das aufgenommene Spektrum der dynamischen Lichtstreuung für die Silica-Probe mit Teilchendurchmesser d = 3, 01 µm.
Abbildung 19: Das Diagramm zeigt das aufgenommene Spektrum der dynamischen Lichtstreuung für die Latex-Probe mit Teilchendurchmesser d = 1, 5 µm.
22
Fehlerbetrachtung Die leider nicht deutbaren Diagramme, die unsere Messungen der
dynamischen Lichtstreuung liefern, könnten unterschiedliche Fehlerquellen haben. Am stärksten wiegt die Vermutung, dass die Messung durch äußere Einflüsse wie z.B. minimale Windstöße verzerrt wurde. Es lies sich im Experiment beobachten, dass bereits eine minimale
Änderung der äußeren Versuchsbedingungen eine größere Veränderung des Musters zur
Folge hat. Insgesamt ist das Rauschen der Diagramme so stark, dass selbst die Korrektur mittels Autokorrelation, die das Programm automatisch vornimmt, dies nicht beheben
kann.
Generell ist es hier jedoch relativ schwierig den Fehler genau zu lokalisieren, weshalb wir
die Untersuchung der dynamischen Lichtstreuung mit diesem Versuchsaufbau leider nicht
empfehlen können.
4.2 Versuchsteil 2: Diffraktive Optik
4.2.1 Abhängigkeit des Drehwinkels von der Wellenlänge
Um diese Abhängigkeit zu zeigen, plotten wir die gemessene Intensität-Werte zusammen
mit den Theoriewerten ohne den SLM nach dem Gesetz von Malus in ein Diagramm
(Abb. 20).
Abbildung 20: Diagramm der Intensiät aufgetragen über dem Winkel α des Analysators.
Der Winkel zum Polarisator beträgt also α + 90◦ .
Man kann sehr gut erkennen, dass Licht einer höheren Wellenlänge weniger weit gedreht
wird 8 .
Da für alle Analysatorstellungen noch eine Intensität gemessen wird, kann das Licht beim
Austreten aus dem SLM nicht mehr linear polarisiert sein.
4.2.2 Bestimmung der Pixelgröße
Da das abgebildete Objekt gerade dem Quadrat mit der Kantenlänge von 400 Pixeln
entspricht, ergibt sich die Pixelgröße `geom aus dem Verhältnis der Gegenstanshöhe hg und
8
Da Analysatorstellungen verschiebungssymmetrisch zu einem Winkel von 180◦ sind, wird hier eine Drehung der Polarisationsebene in negative Richtung angenommen
23
der Pixelzahl n. Nach den Gesetzen der geometrischen Optik gilt dann:
`geom =
δ`geom =
g
b
· hb
hb · f
=
n
(b − f ) · n
2 2
δhb · f
δb · hb · f
+
(b − f ) · n
((b − f ) · n)2
hg
=
n
s
(6)
Damit erhalten wir den Wert `geom = 32, 01(48)µm, welcher mit dem Literaturwert von
32µm sehr gut übereinstimmt.
Um die Breite der Pixel mit Hilfe der Beugung zu ermitteln, berechnen wir zunächst den
Winkel α2 , unter dem das 2. und α5 , unter dem das 5. Maximum abgebildet wurden:
d
α = arctan( )
f
δd
δα =
2
1 + fd2
(7)
Damit erhalten wir α2 = 0, 0337(5)rad und α5 = 0, 0823(5)rad.
Daraus lässt sich nun über die Beziehung 14 die Breite der Pixel `beug bestimmen, wobei
der Fehler sich ergibt zu:
δ`beug,k
δα · kλ cos(α) =
sin(α)2
(8)
Tabelle 6: Berechnete Pixelgrößen. `beug bezeichnet den Mittelwert der beiden anderen
Größen. Als Fehler wurde die Standartabweichung gewählt.
`beug,2 [µm] `beug,5 [µm] `beug [µm]
31,54(47)
32,35(8)
31,95(4)
Auch dieser Wert stimmt also sehr gut mit dem Literaturwert überein.
Da unser Laser nahezu paralleles Licht aussendet, können wir zur Berechnung der Pixelgröße `f res mit Hilfe der Fresnelschen Zonenplatten die Näherung für g f verwenden.
Der Literaturwert liegt auch hier gerade noch in der Toleranz, sodass die im Handbuch
abgedruckte Pixelbreite durch alle Messungen bestätigt wird.
Bei der Messung mit Hilfe der Fresnelschen Zonenplatten weicht der gemessene Wert
jedoch besonders stark vom Literaturwert ab. Einerseits kann diese Abweichung dadurch
begründet werden, dass das Licht des Lasers nur sehr ungenau parallelisiert werden konnte
und die zur Berechnung verwendete Näherung daher ungenau wird, andererseits aber auch
dadurch, dass die Brennweite der Zonenplatte nicht sehr genau bestimmt werden konnte.
24
Tabelle 7: Mit den Fresnelschen Zonenplatten berechnete Werte für `f res und der Durchschnittswert mit empirischer Standardabweichung
Pixel f [cm] `f res [µm]
10
18,5
31,38(42)
15
42,5
31,70(18)
20
72
30,94(10)
12
28,5
32,44(28)
25
103
29,61(71)
`f res
31,22(105)
5 Fragen und Antworten
5.1 Fragen zum Versuchsteil: Lichtstreuung
1. Zeigen Sie durch zweimalige Anwendung des Snelliusschen Brechungsgesetzes, das der sich im Experiment ergebende Winkel für die Ausbreitung in
Luft unabhängig davon ist, ob das Licht zwischen der wässrigen Lösung und
der Luft noch eine zusätzliche Glasscheibe durchläuft.
Hierbei sei angenommen, dass es zu keiner Totalreflexion kommt. Abbildung (21) verdeutlicht den Sachverhalt. Für die Brechung oben gilt nach Gleichung (1):
nL · sin(α1 ) = nG · sin(β)
(9)
Weiter gilt für die Brechung unten ebenfalls nach Gleichung (1):
nG · sin(β) = nL · sin(α2 )
(10)
Der Vergleich von Gleichungen (9) und (10) liefert:
nL · sin(α1 ) = nL · sin(α2 )
⇔
α1 = α2
2. Simulieren Sie die Streuung in der Erdatmosphäre als Streuung an sehr kleinen “Luftkugeln“ im Vakuum.
a) Was hat die unterschiedliche Streuintensität für die verschiedenen Wellenlängen mit der blauen Farbe des Himmels zu tun?
b) Bienen können die Polarisationsrichtung und den Polarisationsgrad von
Licht sehen und nutzen dies zur Feststellung der Sonnenrichtung für den Fall,
dass bei insgesamt geringer Bewölkung die Sonne selbst hinter einer Wolke
verschwindet. Bei welchem Winkel ist der Polarisationsgrad des Lichtes am
höchsten?
zu a) Wie bereits in Abschnitt 2.1.1 erläutert wurde, wird kurzwelliges blaues Licht
stärker gestreut als langwelliges rotes Licht. Da für kurzwelliges Licht die Streuintensität dementsprechend höher ist, wird dieses in der Atmosphäre gestreut und der Himmel
erscheint blau.
25
Abbildung 21: Die Skizze zeigt den Strahlengang von Licht durch eine Glassscheibe. Entscheidend ist hier, dass aufgrund der Symmetrie die Winkel β, die den Winkel in der Glasscheibe jeweils oben und unten zum Lot messen, gleich sind.
zu b) Wie in Abbildung (22) zu erkennen, ist der Polarisationsgrad für einen Einfall des
Sonnenlichts unter einem Winkel von α = 90◦ am höchsten. Hier wird der parallele Anteil
des Sonnenlichts gar nicht gestreut und wir sehen lediglich den senkrechten Anteil des
Lichtes, da dieser über alle Winkel gleichmäßig gestreut wird. Auch dies ist in Abbildung
(22) zu erkennen - hier sind die Graphen für die Intensität des senkrechten Anteils eine
Gerade parallel zur x-Achse.
Abbildung 22: Die Skizze zeigt die Intensität des Sonnenlichts, das in der Atmosphäre
gestreut wird in Abhängigkeit dessen Einfallswinkel. Dabei wird der senkrechte Anteil gleichmäßig gestreut, weshalb deren Graphen eine Gerade ist,
hingegen der parallele Anteil ungleichmäßig gestreut wird.
26
5.2 Fragen zum Versuchsteil: Diffraktive Optik
1. Erklären sie die Funktionsweise einer nematischen Drehzelle
Frage 1 wurde bereits auf Seite 14 beantwortet.
2. Leiten sie das Gesetz von Malus für die durch im Winkel α gegeneinander
verdrehte Polarisatoren transmittierte Intensität her.
Die elektromagnetische Welle habe nach dem Durchlaufen des ersten Polarisators die Amplitude E0 des elektrischen Feldes und sei linear polarisiert. Dann können wir nun die
Welle als Superposition zweier wiederum linear polarisierten Wellen mit den Amplituden
E⊥ = E0 · sin(α) und Ek = E0 · cos(α) auffassen, welche senkrecht beziehungsweise parallel zur Ausrichtung des zweiten Polarisators polarisiert sind. Hinter dem zweiten Polarisator
beträgt die Amplitude des elektrischen Feldes also nur noch E1 = Ek = E0 · cos(α). Über
den Zusammenhang I = |~(E)|2 folgt für die Intensität I hinter dem zweiten Polarisator
I = I0 · cos2 (α)
(11)
3. Begründen Sie, warum die in 23 gezeigte Anordnung von Polarisatoren für
α = 45◦ bei Bestrahlung mit dem Licht einer Glühlampe eine nichtverschwindende Intensität durchlässt. Berechnen Sie den Anteil dieser Intensität an der
Ausgangsintensität I0 . Geben sie den Anteil der transmittierten Intensität allgemein in Abhängigkeit von α an.
Abbildung 23: Vergleich unterschiedlich polarisierter Wellen[Run11]
Die Intensität I1 hinter dem zweiten Polarisator beträgt nach 11 I1 = I0 · cos2 (α), wobei
I0 die Intensität des Lichtes hinter dem ersten Polarisator bezeichnet. Analog gilt für die
Intensität I2 hinter dem dritten Polarisator
I2 = I0 · cos2 (α) · cos2 (90 − α) = I0 · cos2 (α) · sin2 (α)
(12)
3. Nennen und beschreiben Sie drei Verfahren zur Herstellung von linear polarisiertem Licht aus unpolarisiertem Licht.
27
Die Verfahren zur Erzeugung linear polarisierten Lichtes wurden bereits im Grundlagenteil
im Kapitel Polarisation (2.2) hergeleitet.
4. Leiten Sie die Beziehung sin α = k · λ mit k = 0, 1, 2, 3, ... für die Winkel α
k
g
k
her, unter denen bei Beugung von Licht der Wellenlänge λ an einem Gitter mit
Gitterkonstante g Beugungsmaxima auftreten.
Wie aus Abb. 24 entnommen werden kann, gilt für den Gangunterschied d bei der Beugung
am Gitter der Zusammenhang
d = g · sin(ϕ)
(13)
Für konstruktive Interferenz muss der Gangunterschied d zwischen den verschiedenen
Lichtstrahlen ein ganzzahliges Vielfaches von λ sein. Für Maxima gilt also:
k · λ = g · sin(ϕ)
k·λ
sin(ϕk ) =
g
(14)
Abbildung 24: Zusammenhang zwischen Gangunterschied d, Winkel ϕ und der Gitterkonstanten g bei der Beugung am Gitter[Wik]
q
·g
5. Leiten Sie für die Fresnelsche Zonenplatte die Beziehung rn = nλ · ff +g
zwischen dem Radius rn der n-ten Zone, der Wellenlänge λ des Lichts, der
Bildweite f und der Gegenstandsweite g her. Was lässt sich über die chromatische Aberration einer Zonenplatte aussagen? Ist die Brennebene eindeutig
bestimmt?
Die Herleitung für die Berechnung der rn wurde bereits im Grundlagenteil bearbeitet. Da
die Breite der Ringe sehr stark wellenlängenabhängig ist, ist die chromatische Aberration
einer Zonenplatte sehr hoch, weshalb sie ausschließlich für die Fokussierung monochromatischer Wellen verwendet wird. Die Brennebene der Zonenplatte kann also auch nicht
eindeutig festgelegt sein, da Licht unterschiedlicher Wellenlängen unterschiedlich weit fokussiert wird.
28
Tabellenverzeichnis
1
2
3
4
5
6
7
Normierte Messwerte zur Bestimmung der Wellenlängenabhänigkeit der Drehung der Polarisationsebene . . . . . . . . . . . . . . . . . . . . . . . . . . .
Wertetabelle zur Messung der Brennweite b in Abhängigkeit vom Radius r1
der innersten Fresnelschen Zone . . . . . . . . . . . . . . . . . . . . . . . .
Streuwinkel der Maxima und Minima der einzelnen Proben . . . . . . . . .
Ursprüngliche Streuwinkel der Maxima und Minima der einzelnen Proben .
Vergleich der Teilchendurchmesser . . . . . . . . . . . . . . . . . . . . . . .
Berechnete Pixelgrößen. `beug bezeichnet den Mittelwert der beiden anderen
Größen. Als Fehler wurde die Standartabweichung gewählt. . . . . . . . . .
Mit den Fresnelschen Zonenplatten berechnete Werte für `f res und der
Durchschnittswert mit empirischer Standardabweichung . . . . . . . . . . .
17
17
18
19
19
24
25
Abbildungsverzeichnis
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
Lichtstreuung in der Atmosphäre . . . . . . . . . . . . . . . . . . . . . . . .
Vergleich unterschiedlich polarisierter Wellen[Wik11] . . . . . . . . . . . . .
Prinzip der Drahtgitterpolarisation[Wik11] . . . . . . . . . . . . . . . . . . .
Indexellipsoid eines uniaxialen Kristalles. [Wik] . . . . . . . . . . . . . . . .
Snelliussches Brechungsgesetz . . . . . . . . . . . . . . . . . . . . . . . . .
Idealisierte Beugung am Spalt . . . . . . . . . . . . . . . . . . . . . . . . . .
Beugung am Spalt: Fraunhofer- und Fresnelsche Beugung . . . . . . .
Zusammenhang zwischen Gangunterschied d, Winkel ϕ und der Gitterkonstanten g bei der Beugung am Gitter . . . . . . . . . . . . . . . . . . . . . .
Bild einer binären Fresnelschen Zonenplatte. [Wik11] . . . . . . . . . . . .
Aufbau einer einfachen Flüssigkristallanzeige[FK] . . . . . . . . . . . . . . .
Aufbau einer einfachen Flüssigkristallanzeige[Wik11] . . . . . . . . . . . . .
Lichtstreuung - Versuchsaufbau . . . . . . . . . . . . . . . . . . . . . . . . .
Diffraktive Optik - Versuchsaufbau . . . . . . . . . . . . . . . . . . . . . . .
Diffraktive Optik - Versuchsaufbau . . . . . . . . . . . . . . . . . . . . . . .
simulierte Streuung für Licht der Wellenlänge λ = 532 nm in einer SilicaLösung mit von uns vermutetem Teilchendurchmesser dS = 2, 7 µm . . . . .
simulierte Streuung für Licht der Wellenlänge λ = 532 nm in einer LatexLösung mit von uns vermutetem Teilchendurchmesser dS = 1, 5 µm . . . . .
simulierte Streuung für Licht der Wellenlänge λ = 532 nm in einer LatexLösung mit von uns vermutetem Teilchendurchmesser dS = 4, 6 µm . . . . .
Dynamische Lichtstreuung - Spektrum der Silica-Probe mit Teilchendurchmesser d = 3, 01 µm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Dynamische Lichtstreuung - Spektrum der Latex-Probe mit Teilchendurchmesser d = 1, 5 µm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Diagramm der Intensiät aufgetragen über dem Winkel α des Analysators.
Der Winkel zum Polarisator beträgt also α + 90◦ . . . . . . . . . . . . . . . .
Strahlengang von Licht durch eine Glassscheibe . . . . . . . . . . . . . . . .
Intensität des in der Atmosphäre gestreuten Sonnenlichts in Abhängigkeit
dessen Einfallswinkel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
Vergleich unterschiedlich polarisierter Wellen[Run11] . . . . . . . . . . . . .
29
5
6
7
8
10
10
11
12
13
13
14
15
16
16
20
20
21
22
22
23
26
26
27
24
Zusammenhang zwischen Gangunterschied d, Winkel ϕ und der Gitterkonstanten g bei der Beugung am Gitter[Wik] . . . . . . . . . . . . . . . . . . . 28
Literatur
[Dem09] Wolfgang Demtröder:Experimentalphysik 2 Elektrizität und Optik SpringerVerlag, BerlinHeidelberg, 2009.
[Gre07] Walter Greiner:Klassische ElektrodynamikVerlag Harri Deutsch Frankfurt am
Main, 2007.
[Nol06] Nolting,
Wolfgang:Grundkurs
Theoretische
ElektrodynamikSpringer-Verlag, Berlin Heidelberg, 2006.
Physik
3
-
[Run11] ap.physik.uni-konstanz.deVersuchsanleitungen, Stand 29.05.2011.
[Ger06] Dieter Meschede:Gerthsen PhysikSpringer-Verlag, Berlin Heidelberg, 23. Aufage, 2006
[Stö10] Horst Stöcker:Taschenbuch der PhysikVerlag Harri Deutsch Frankfurt am
Main, 2010.
[Wik] Wikipedia:Freie EnzyklopädieStand 24.06.2011
[FK]
Flüssigkristalle:http://fluessigkristalle.com
[Sacc] Eigenes Versuchsprotokoll zu den Versuchen Saccharimetrie und Faraday-Effekt
[Beug] Eigenes Versuchsprotokoll zu den Versuchen Beugung am Gitter und Interferometer
30